Соловьев В.И. Математические методы управления рисками
Подождите немного. Документ загружается.


Если даже считать, что на рынке обращается 500 акций
(
ровно столько акций представлено в популярном фондовом ин>
дексе Standard & Poor’s 500 — см. далее; на самом деле, акций
на рынке обращается больше), то если взять данные за месяц
(22
рабочих дня, по одной котировке в день), то получится
220
◊
500 = 11 000 чисел, а оценить нужно 500 средних
k
e , 500 во>
латильностей
ˆ
и 124750 ковариаций
k
s
cov( ; )
kj
EE — точность
полученных таким способом оценок будет весьма низкой. Если
брать более длительные промежутки времени, то точность оце>
нок все равно будет невысокой в силу того, что рыночная конъ>
юнктура меняется очень быстро, иногда за неделю происходят
весьма и весьма значительные изменения! Что же делать?
Выход довольно прост: рассматривать зависимость эффек>
тивностей акций от каких>либо ведущих факторов, объ>
ективно характеризующих финансовый рынок в це>
лом. В качестве такого ведущего фактора можно взять, напри>
мер, цены на энергоносители; все компании пользуются энерги>
ей — и в технологических процессах, и в процессе перевозок,
поэтому эффективность работы компаний напрямую зависит от
изменений цен на энергоносители.
Рассмотрим зависимость эффективности акции E от неко>
торого фактора F; в простейшем случае такую зависимость
можно представить в виде модели линейной регрессии
E
k
= a
k
+ b
k
F + e
k
, (3.3.12)
где k — номер акции, a
k
и b
k
— некоторые постоянные, а
e
k
~ N(0; s
e
k
) — случайный эффект влияния на доходность E
k
не>
контролируемых факторов.
Коэффициент b
k
имеет смысл чувствительности доходности
E
k
данной акции к изменениям рыночного фактора F.
В качестве F часто выбирают какой>либо фондовый ин
декс — среднее взвешенное курсов акций важнейших эмитен>
тов рынка акций; чаще всего используются следующие фондо>
вые индексы:
• индекс Доу — Джонса — первый в мире фондовый индекс,
предложенный в 1884 г. журналистом Ч. Доу и его партнером по
выпуску газеты Wall Street Journal Э. Джонсом; в настоящее время
рассчитываются индексы Доу — Джонса для различных групп
компаний, например, индекс Dow Jones Industrial рассчитывается
72

по 30 крупнейшим промышленным корпорациям США
(
http://indexes.dowjones.com/);
• индекс Standard & Poor’s 500 — взвешенный по рыночной
стоимости индекс 500 акций крупнейших американских компаний,
из которых 400 относятся к промышленности, 40 — к энергетике,
40 —
к сфере финансов, а оставшиеся 20 — к транспорту
(
http://www.standardandpoors.com/);
• индекс обыкновенных акций Financial Times — самый пер>
вый фондовый индекс в Европе, появившийся на страницах газеты
Financial Times
в 1935 г.; рассчитывается как средняя геометриче>
ская котировок акций 100 ведущих британских компаний
(
http://www.ftse.com/);
• индекс РТС; рассчитывается по данным 62 акций (в кон>
це 2003 г.), обращающихся в Российской торговой системе
(
http://www.rts.ru/);
• индекс S&P/RUX; рассчитывается по данным 46 акций
(
в конце 2003 г.), обращающихся в Российской торговой системе
(
http://www.rts.ru/);
•
индекс AK&M; рассчитывается по данным 36 (в конце
2003
г.) ведущих российских эмитентов акций
(
http://www.akm.ru/
).
Если в модели (3.3.12), в которой в качестве F выбран некото>
рый фондовый индекс, равный усредненной доходности различ>
ных акций, обращающихся на рынке, и оценка значения b ока>
зывается больше единицы, это означает, что данная акция явля>
ется агрессивной, т. е. ее доходность растет в среднем быстрее,
чем доходность по рынку в целом; если оценка b оказывается
меньше единицы, это означает, что данная акция является обо
ронительной, ее доходность растет в среднем медленнее, чем
доходность по рынку; для некоторых ценных бумаг оценка ко>
эффициента b близка к нулю, это значит, что ожидаемая доход>
ность данной бумаги не зависит (или почти не зависит) от пове>
дения рынка. Возможны случаи положительных и отрицатель>
ных коэффициентов b, в этих случаях доходность данной акции
изменяется соответственно в том же направлении, что и доход>
ность по рынку в целом или в противоположном направлении.
Если в модели (3.3.12) в качестве F выбрать
F = r
M
– i,
73
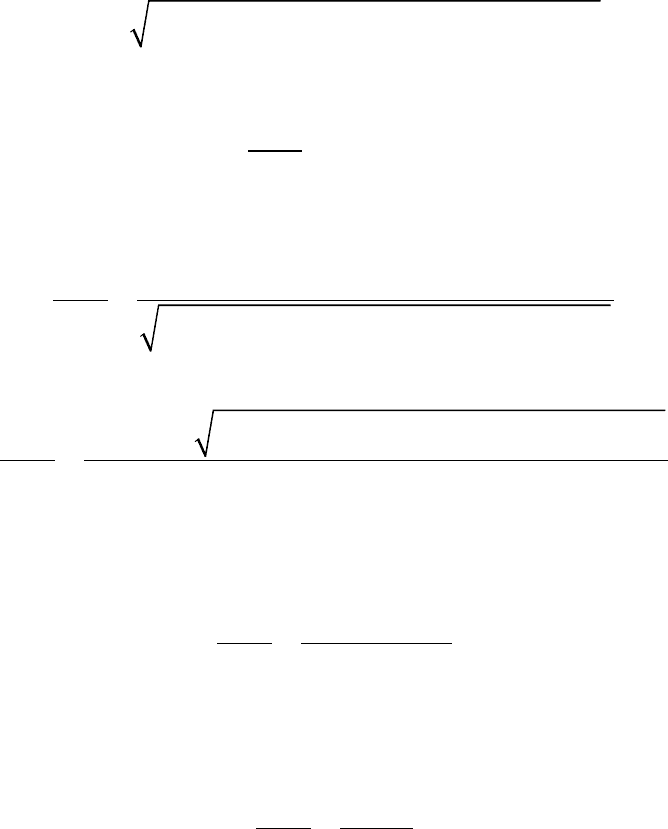
где r
M
— доходность касательного портфеля p
M
, i — процентная
ставка безрисковых вложений и заимствований, то получим
следующую регрессионную модель:
E
k
= a
k
+ b
k
(r
M
– i) + e
k
.
Рассмотрим портфель p, в который входит k>я акция с до>
лей x
k
и рыночный портфель p
M
с долей (1 – x
k
); его доходность
будет равна
E
p
= x
k
E
k
+ (1 – x
k
)r
M
,
дисперсия доходности
,
22 22
,
(1 ) 2 (1 )
kk k M k k kM
Ex x x x=s+- s+ - sD
p
среднее квадратичное отклонение (риск)
22 22
,
(1 ) 2 (1 )
kk k M k k kM
xxxxs= s+ - s + - s
p
. (3.3.13)
Производная
kM
k
dE
Er
dx
=-
p
,
из равенства (3.3.13) получаем, что
22 2
,,
22 22
,
2
(1 ) 2 (1 )
kk M kM kkM
k
kk k M k k kM
xx
d
dx
xxxx
s-s +s - s
s
=
s+ - s + - s
p
,
поэтому
22 22
,
22 2
,,
( ) (1 ) 2 (1 )
2
kM kk k M k kkM
kk M kM kkM
Er x x x x
dE
dx x
-s+-s+-s
=
s s -s +s - s
p
p
.
Точка касательного портфеля означает, что в k>ю акцию
вложена доля x
k
= 0, поэтому в этой точке
2
,
()
kMM
kM M
dE E r
d
-s
=
ss-s
p
p
. (3.3.14)
Но кривая в этой точке касается прямой, соединяющей точ>
ки e и p
M
, наклон которой равен
M
M
dE r i
d
-
=
ss
p
p
. (3.3.15)
Приравняв правые части (3.3.14) и (3.3.15), получим:
74
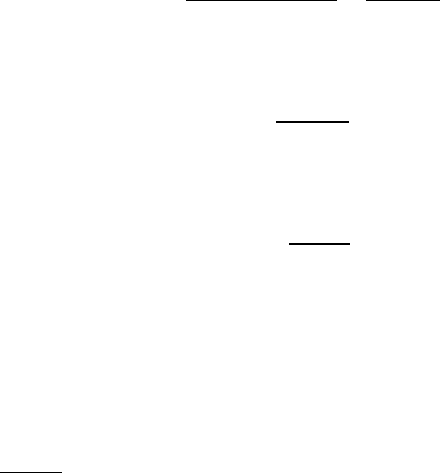
2
,
()
kMM M
kM M M
Er r-s -
=
s-s s
i
.
откуда
2
,
2
() (
M
kM kM M
M
ri
Er
-
-= s-s
s
)
или
,
2
()
kM
kM
M
Ei ri
s
=+ -
s
.
Окончательно получаем, что для произвольной акции с но>
мером k
, (3.3.16)
,
(
kkMM
Ei r i-=b -)
где
,
,
2
kM
kM
M
s
s
b=
, а свободный член равен безрисковой процентной
ставке i.
Модель (3.3.16), описывающая зависимость премии за риск
E
k
– i для данной акции с номером k от премии за риск r
M
– i по
рынку в целом, называется моделью оценки основных активов
(Capital Asset Pricing Model).
Она была предложена в 1964 г.
У. Шарпом (Нобелевским лауреатом 1990 г.) в работе [43]. Ли>
ния, которая задается уравнением (3.3.16) называется рыноч
ной линией ценной бумаги (Security Market Line).
Кроме очевидной задачи, отмеченной в начале пункта, есть и
еще одно важное практическое применение модели оценки ос>
новных активов, которое заключается в том, что данная модель
может позволить выявить неверно оцененные акции: если
реально наблюдаемая доходность акции выше (или ниже) той, что
определяется моделью оценки основных активов, то такая акция
называется недооцененной (соответственно переоцененной); эта
разница образуется в результате рыночного неравновесия и
должна со временем исчезнуть. Таким образом, представляется
выгодной покупка недооцененных акций в ожидании повышения
их доходности, а также игра на высокодоходных, но переоценен>
ных, акциях (которая, конечно, может быть только краткосроч>
ной).
ПРИМЕР 3.3.2. Табл. 3.3.1 содержит данные о значениях до>
ходности некоторой акции E и доходности рыночного портфеля
r
M
за последние 10 дней.
Таблица 3.3.1
75
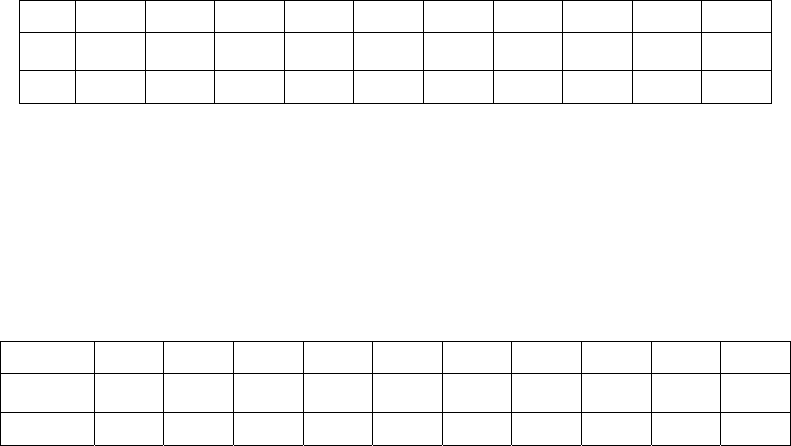
Изменения доходностей акции и рыночного портфеля
t
1 2 3 4 5 6 7 8 9 10
r
M, t
0,13 0,15 0,11 0,12 0,14 0,13 0,15 0,13 0,14 0,17
E
t
0,16 0,21 0,13 0,14 0,15 0,14 0,24 0,15 0,18 0,23
Какой коэффициент b имеет данная акция, если ставка
банковского процента равна 10% годовых?
Решение. Вначале перейдем от доходностей к премиям за риск:
табл. 3.3.2.
Таблица 3.3.2
Изменения премии за риск для акции и для рыночного портфеля
t
1 2 3 4 5 6 7 8 9 10
r
M, t
– i
0,03 0,05 0,01 0,02 0,04 0,03 0,05 0,03 0,04 0,07
E
t
– i 0,06 0,11 0,03 0,04 0,05 0,04 0,14 0,05 0,08 0,13
Введем данные табл. 3.3.2. в рабочий лист Microsoft Excel, как показа>
но на рис. 3.3.4, а и воспользуемся программой «Регрессия» инструмента
«Анализ данных». Для этого выберем в меню «Сервис» пункт «Сервис | Ана!
лиз данных…», и из появившегося списка программ анализа данных выбе>
рем программу «Регрессия». В появившемся окне (рис. 3.3.4, б) укажем,
что значения зависимой переменной (премии за риск для данной акции
Y = = E – i) содержатся в интервале $C$1:$C$11(«Входной интервал Y»),
значения независимой переменной (премии за риск для рыночного порт>
феля x = r
M
– i) содержатся в интервале $B$1:$B$11 («Входной интервал
X»), в первой строке указанных диапазонов находятся наименования пе>
ременных («Метки»), а уравнение регрессии Y = bx + e не содержит сво>
бодного члена («Константа — ноль»). Результаты выведем на новый рабо
чий лист, запросим также построение графика подбора.
Поясним смысл наиболее важных результатов работы программы
(рис. 3.3.4, в).
Регрессионная статистика:
1. Множественный R = 0,88 – такова, судя по наблюдениям, степень
линейной зависимости премии за риск для данной акции Y = E – i от пре>
мии за риск для рыночного портфеля X = r
M
– i, (множественный R – это
оценка коэффициента корреляции
ˆ
).
(; ) ,880XY=r
2. R!квадрат = 0,77 – судя по наблюдениям, 77% вариации котиров>
ки акции Y связано с линейным влиянием курса доллара .
Дисперсионный анализ:
1. В п е р в о й таблице приведены результаты, необходимые для
проверки гипотезы H
0
: b = 0 (неизвестный параметр b линейного уравне>
ния регрессии Y = bx + e равен нулю). Если Значимость F больше требуе>
мого уровня значимости a (как привило, принимают a = 0,05), то гипоте>
зу H
0
принимают: линейное уравнение регрессии Y = bx + e лишено
смысла и отвергается; если же Значимость F меньше a, гипотезу H
0
отвер>
76
гают: регрессионная модель правомерна. В примере Значимость F соста>
вила 0,0006 — значит, модель правомерна.
2. Во в т о р о й таблице:
а)
Y
!пересечение
=
0 — это оценка свободного члена уравнения регрессии,
б) Коэффициент r
M
– i = 1,99 – это оценка коэффициента b,
77

A B C
1
t
r
M
–
i
E –
i
2
1 0,03 0,06
3
2 0,05 0,11
4
3 0,01 0,03
5
4 0,02 0,04
6
5 0,04 0,05
7
6 0,03 0,04
8
7 0,05 0,14
9
8 0,03 0,05
10
9 0,04 0,08
11
10 0,07 0,13
а) ввод исходных данных
б) окно «Регрессия»
A B C D E F G
1
ВЫВОД ИТОГОВ
2
3
Регрессионная статистика
4
Множественный R 0,88
5
R!квадрат 0,77
6
Нормированный
R!квадрат
0,66
7
Стандартная ошибка 0,019
8
Наблюдения 10
9
10
Дисперсионный анализ
11
df SS MS F Значимость F
12
Регрессия 1 0,0111 0,0111 30,32 0,0006
13
Остаток 9 0,0032 0,0004
14
Итого 10 0,0141
15
16
Коэффициен
ты
Стандарт
ная ошибка
tста
тистика
Pзна
чение
Нижние
95%
Верхние
95%
17
Y!пересечение 0 #Н/Д #Н/Д #Н/Д #Н/Д #Н/Д
18
r
M
– i 1,99 0,15 13,26 0,0000003 1,65 2,33
0,05
0,10
0
0,02 0,04 0,06
E
– i
r
M
– i
в) результаты
Рис. 3.3.4. Расчеты в примере 3.3.2
78
Окончательно линейное уравнение регрессии принимает вид:
Y = bx + e = 1,99x + e
или
E – i = b(r
M
– i) + e = 1,99(r
M
– i) + e.
Во второй строке этой таблицы приведена 95%>ная интервальная
оценка параметра b: 1,65 < b < 2,33.
Подведем итог. Модель
E – i = 1,99(r
M
– i) + e
зависимости премии за риск для данной акции Y = E – i от премии за
риск для рыночного портфеля x = r
M
– i правомерна, так как гипотеза
H
0
: b = 0 отвергается при 5%>ном уровне значимости. Полученное урав>
нение регрессии имеет достаточно хорошие характеристики:
близок к своему максимальному значению, равному едини>
це. Поэтому уравнение можно использовать для прогноза премии за риск
для данной акции Y = E – i при известном значении премии за риск для
рыночного портфеля x = r
M
– i.
(; ) ,88
ˆ
0XY=r
Точечная оценка параметра
ˆ
говорит о том, что при увеличе>
нии (r
M
– i) на единицу можно ожидать роста премии за риск для данной
акции (E – i) на 1,99, при этом с 95%>ной гарантией премия за риск для
данной акции не увеличится более, чем на 2,33 и менее, чем на 1,65.
1, 9 9b=
График подбора, также приведенный на рис. 3.3.4, в, демонстрирует
соответствие модели (жирная прямая) и реальных наблюдений (точки).
3.3.3. Стоимость фирмы и структура капитала
Предположим, что мы владеем некоторым бизнесом (фир>
мой) и хотим этот бизнес продать. Возникает важный вопрос оп>
ределения стоимости этого бизнеса. Если фирма представ>
ляет собой открытое акционерное общество, его акции торгуются
на бирже, и мы владеем 100% акций, то вопрос этот решается
очень просто: стоимость фирмы равна рыночной цене одной ак>
ции, умноженной на количество выпущенных акций. Если мы
владеем не всеми акциями фирмы, а некоторой их долей, то на>
ша доля стоит ровно столько, сколько стоят наши акции. Следу>
ет, конечно, учесть тот факт, что многие компании имеют дол>
говые обязательства перед банками и держателями облигаций:
рациональная стоимость такой фирмы должна быть получена
как сумма стоимости всех акций фирмы и суммы долгов.
Итак, если w
S
— доля акций в структуре капитала фирмы,
S
t
— суммарная стоимость всех акций в настоящий момент
времени, w
B
— доля долговых обязательств в структуре капи>
тала фирмы, B
t
— суммарная стоимость всех долгов компании в
79
настоящий момент времени, то средняя взвешенная стоимость
капитала WACC (Weighted Average Cost of Capital) определя>
ется как
WACC = w
S
S
t
+ w
B
B
t
. (3.3.17)
Можно решать и обратную задачу: вначале опреде>
лить стоимость фирмы, а затем вычесть стоимость долговых
обязательств и разделить остаток на количество акций компа>
нии — при этом мы получим рациональную стоимость одной
акции. Если рыночная цена акции окажется ниже этой величи>
ны, то такие акции имеет смысл приобрести, потому что в на>
стоящий момент рынок их недооценивает, но со временем их
цена должна стать ближе к рациональной стоимости.
ПРИМЕР 3.3.3. Фирма имеет капитал, в структуре которо>
го 30% составляют облигации и 70% — акции. Всего было выпу>
щено по 10 000 акций и облигаций, текущая рыночная цена од>
ной акции равна 1000 руб., а текущая рыночная цена облигации
равна 400 руб. Чему равна средняя взвешенная стоимость ка>
питала этой фирмы?
Решение. По формуле (3.3.17) имеем: WACC = w
S
S
t
+ w
B
B
t
. =
= 0,3◊10 000◊400 + 0,7◊10 000◊1000 = 8 200 000.
Акционерные общества создаются для извлечения доходов,
доходы эти выплачиваются акционерам в форме дивидендов,
поэтому стоимость компании должна совпадать с современной
стоимостью всех будущих дивидендов по акциям и процентных
выплат по облигациям. Если бизнес имеет форму, отличную от
корпорации (акционерного общества), то его стоимость можно
рассчитать точно так же — как современную стоимость потока
платежей, соответствующего деятельности фирмы. Можно
пойти и другим путем: исходя из информации о стоимости со>
поставимого акционерного общества.
ПРИМЕР 3.3.4. Бизнес одного из первокурсников состоит в
том, что он установил копировальный аппарат в здании универ>
ситета. Одна копия стоит 3 руб., студенты заказывают в сред>
нем 20 000 копий в год. Оборудование обошлось предпринима>
телю в 40 000 руб., при этом ежегодные расходы на амортиза>
цию равны 10 000 руб., арендная плата за университетское по>
мещение составляет 20 000 руб., а ставка банковского процента
равна 10%. Стоит ли открывать такой бизнес, если считать, что
через пять лет, когда предприниматель закончит университет,
этот бизнес придется продать, а срок службы копировального
аппарата составляет 10 лет (для упрощения расчетов принять
80

предположение, что поступление доходов и осуществление
расходов происходит строго в конце каждого года)?
Решение. В конце каждого года из будущих десяти лет предпринима>
тель будет получать доход
C = 20 000◊3 – 10 000 – 20 000 = 30 000 руб.
Чистая приведенная стоимость потока платежей, поступающих за
весь период работы фирмы, по формуле (3.3.1) равна
10
30 000(1 1,1 )
184 337,01=
0,1
-
-
==NPV
184 337
руб. 01 коп.,
и поскольку открытие такого бизнеса обходится всего в NPI = 40 000 руб.,
бизнес это выгоден.
Через пять лет стоимость бизнеса будет равна
5
5
30 000(1 1,1 )
113723,60
руб. 113723 руб.60коп.
0,1
-
-
===
NPV ;
именно за такую сумму справедливо продать бизнес. При этом суммар>
ный приведенный доход, который за пять лет будет получен владельцем
бизнеса, равен
5
5
15
начальные
приведенный доход
инвестиции
от продажи бизнеса
приведенный доход
от использования бизнеса
в течение пяти лет
30 000(1 1,1 )
40000 113 723,60 1,1
0,1
40000 113723,6
-
-
-
-
-=- + + ◊=
=- +
NPV NPI
0 70 613,41 144 337,01руб. 144 337 руб. 01коп.+= =
Таким образом, бизнес открывать стоит.
Обсудим теперь, каким образом стоимость фирмы зависит от
структуры капитала, т. е. от соотношения между w
S
и w
B
.
Рассмотрим две фирмы: А, которая имеет стоимость
V
А
ден. ед., финансируется только за счет выпуска акций общей
стоимостью S
А
ден. ед., и Б, которая имеет стоимость V
Б
ден. ед.,
финансируется и за счет выпуска акций общей стоимостью
S
Б
ден. ед., и за счет выпуска облигаций общей стоимостью
B
Б
ден. ед. С точки зрения эффективности бизнеса обе фирмы
абсолютно одинаковы, т. е. приносят инвесторам одинаковую
прибыль E ден. ед. за базовый период времени (например, за
год). Долговые обязательства рассмотрим самые простые: фир>
ма обязуется в течение бесконечно долгого периода времени
выплачивать кредитору ежегодные купонные платежи в раз>
мере rB, где B — сумма долга.
81
Пусть инвестор приобрел долю a акций фирмы А и запла>
тил за это aS
А
ден. ед.; при этом V
А
= S
А
, так как фирма А фи>
нансируется только за счет акций. В результате инвестор при>
