Соловьев В.И. Математические методы управления рисками
Подождите немного. Документ загружается.


схемой сложных процентов и предполагает начисление про>
цента не на первоначальную сумму B
0
, а на сумму, лежащую на
счете после последнего начисления процентов, таким образом,
через (целое число) t лет при использовании схемы сложных
процентов на счете будет лежать сумма
B
k
= B
0
(1 + i)
t
.
В конкурентной борьбе за вкладчиков банки предлагали все
новые и новые возможности, например, начисление процентов
не в конце года, а n раз в год. При этом, прежде всего, необходи>
мо как>то сравнивать условия, предлагаемые различными бан>
ками, и для этого договорились всегда называть клиентам про
центы годовых — процентную ставку i, выплачиваемую за год.
Если за год выплачивается процент i, то за n>ю часть года в
случае простых процентов, очевидно, будет выплачи>
ваться процент i
n
= i/n, и через t лет (т. е. через [nt] начислений
процентов) на счете будет лежать сумма
1[ ]
tt
i
BB nt
n
ʈ
=+
Ë
¯
(1.1.1)
(здесь число t может быть уже как целым, так и дробным; квад>
ратными скобками [x] обозначена целая часть числа x — наи>
меньшее целое число, не превосходящее x).
Рассчитаем процентную ставку i
n
, выплачиваемую за n>ю
часть года в случае сложных процентов. За год сумма B
0
увели>
чивается до B
0
(1 + i), с другой стороны, если n раз за этот год
начислялся процент i
n
по схеме сложных процентов, то к концу
года сумма B
0
должна превратиться в B
0
(1 + i
n
)
n
. Таким образом,
заключаем, что
B
0
(1 + i) = B
0
(1 + i
n
)
n
или
1 + i = (1 + i
n
)
n
, (1.1.2)
откуда
i
n
= (1 + i)
1/n
– 1. (1.1.3)
Отсюда следует, что если за год выплачивается процент i, а
в год осуществляется n процентных выплат, то в случае слож>
ных процентов через t лет (т. е. через n[t] + [n{t}] начислений
процентов) на счете будет лежать сумма
12

(
)
[{}]
[]
[][ {}]
[][ {}] 1/
00 0
(1 ) (1 ) (1 )
nt
t
nt nt
nt nt n
n
tn
BB i B i B i
+
+
+
=+ = + =+
(здесь, как и ранее, число t может быть как целым, так и дроб>
ным; квадратными скобками [x] обозначена целая часть числа
x, а фигурными скобками {x} — дробная часть x: {x} = x – [x]).
Итак, в случае с л о ж н ы х п р оцентов, начисляемых n
раз в год,
[{}]
[]
0
(1 )
nt
t
n
t
BB i
+
=+ . (1.1.4)
Дальнейшая конкуренция банков за вклады привела к схе-
ме непрерывных процентов. Пусть сложные проценты начис>
ляются n раз в год, а t = m/n — рациональное число (m и n —
натуральные), тогда
(
)
1/ /
00 0 0
(1 ) (1 ) (1 ) (1 )
m
mnmn
tn
BB i B i B i B i=+= + =+ =+
t
.
Поскольку любое вещественное положительное число t мо>
жет быть сколь угодно точно приближено рациональным чис>
лом m/n, и предполагая зависимость B
t
от i и t непрерывной,
получим формулу начисления непрерывных процентов:
B
t
= B
0
(1 + i)
t
(1.1.5)
для любого t > 0.
При этом интенсивностью процентов d называется мгно>
венная относительная скорость накопления средств на банков>
ском счете при непрерывном начислении процентов:
00
00 0
0
(1 ) (1 )
(1 ) 1
lim lim lim
(1 )
tt t
t
tt t
t
tt t
t
B B Bi Bi
i
Bt B i t t
+D
D
+D
DÆ DÆ DÆ
-+-+
+-
d= = =
D+DD
;
вспомнив второй замечательный предел
0
1
lim ln
x
x
a
a
x
Æ
-
= ,
заключаем, что
d = ln (1 + i). (1.1.6)
Из формул (1.1.5) ~ (1.1.6) следует, что
B
t
= B
0
e
d
t
. (1.1.7)
Рис. 1.1.1, на котором представлены графики функций
= (1 + ti) и = (1 + i)
t
, дает возможность убедиться в
(прост.)
t
v
(непр.)
t
v
13

том, что при t < 1 простые проценты растут быстрее, чем слож>
ные и непрерывные, а при t > 1 — медленнее.
1
v
t
t
0
1
1 + i
Рис. 1.1.1. Сравнение силы роста простых процентов (тонкая линия)
и непрерывно начисляемых процентов (жирная линия)
При расчетах за неполное число лет иногда применяется
комбинированная схема сложных и простых процентов — за
целое число лет начисляются сложные проценты, а за остаток
года — простые:
[]
0
(1 ) (1 { } )
t
t
BB i ti=+ +
Если сумма B
t
, лежащая на банковском счете в момент вре>
мени t, отрицательна (при этом говорят, что на счете образова>
лась короткая позиция), подразумевается, что банк креди>
тует вкладчика на сумму |B
t
|, взимая за это тот же самый про>
цент i, который начисляется на счета с положительной суммой
(
с длинной позицией). Очевидно, модели (1.1.1), (1.1.4), (1.1.5)
и (1.1.7) описывают и случай короткой, и случай длинной пози>
ции на банковском счете.
ПРИМЕР 1.1.1. Через сколько лет удвоится сумма, поло>
женная в банк под i = 10% годовых, если начисления на банков>
ский счет производятся по схеме: а) простых процентов; б)
сложных процентов?
Решение. Через t лет исходная сумма B
0
в случае простых процентов
превратится в B
t
= B
0
(1 + [t]i), а в случае сложных процентов — в B
t
=
= B
0
(1 + i)
[t]
. Чтобы ответить на вопрос, необходимо решить неравенства:
а) B
0
(1 + [t]i) 2B
0
; б) B
0
(1 + i)
[t]
2B
0
или
а) 1 + [t]i 2; б) (1 + i)
[t]
2,
откуда получаем:
а)
11
10
0,1
t
i
==[]
; б)
ln2 ln2 0,693
7,29
ln(1 ) ln1,1 0,095
t
i
== ª
+
[]
.
14

Таким образом, в случае простых процентов сумма удвоится через
10 лет, а в случае сложных процентов — через 8 лет.
Заметим, что в случае непрерывных процентов сумма удвоится за
7,29 лет, т. е. приблизительно за 7 лет и 3,5 мес.
ПРИМЕР 1.1.2. В день рождения сына родители положили
на его банковский счет 50 000 руб. Какая сумма будет на счете к
восемнадцатилетию сына, если банк начисляет сложные про>
центы по ставке i = 10%?
Решение. По формуле (1.1.4) получаем: B
18
= 50 000(1 + 0,1)
18
=
= 50 000
◊
5,5599173 = 277 995,87 руб. = 277 995 руб. 87 коп.
Многие банки в современной России привлекают заемщи>
ков, пользуясь их недостаточной финансовой грамотностью. Это
иллюстрирует
ПРИМЕР 1.1.3. Потребитель взял в кредит 1 000 000 руб. и
должен вернуть через полгода эту сумму и 20% от нее (за поль>
зование кредитом). Какую ставку сложных годовых процентов
взимает данный банк?
Решение. По формуле (1.1.2) имеем: 1 + i = (1 + i
2
)
2
, где i — годовая
процентная ставка, а i
2
= 20% =0,2 — ставка, выплачиваемая за полгода.
Отсюда i = (1 + i
2
)
2
– 1 = (1 + 0,2)
2
–1 = 0,44. Таким образом, если заемщик
выбирает между банком, который взимает 16% годовых и требует гаран>
тий поручителей или оставления залога, и данным банком, то плата за от>
сутствие гарантий составит 44% – 16% = 28% годовых (от 1 000 000 руб.
это составит 280 000 руб. — значительную сумму)!
§ 1.2. ПРИВЕДЕННАЯ СТОИМОСТЬ ДЕНЕГ
Предположим, что мы должны выплатить в момент t > 0 в
будущем некоторую сумму B
t
, и у нас есть возможность вос>
пользоваться банковским счетом, по которому начисляется i
процентов годовых. Какую сумму B
0
можно положить на счет
сегодня (в нулевой момент времени), чтобы к моменту t иметь на
счете в точности требуемую сумму?
Очевидно, суммы B
0
и B
t
связаны равенством (1.1.1) в случае
простых процентов, равенством (1.1.4) — в случае сложных
процентов, и равенством (1.1.5) — в случае непрерывных про>
центов. Для этих трех случаев получаем, соответственно,
0
[{}]
[]
, простые проценты, (1.2.1)
1[ ]
(1 ) , сложные проценты, (1.2.2)
(1 ) e , непрерывные проценты. (1.2.3)
t
nt
t
n
t
tt
tt
B
i
nt
n
B
Bi
Bi B
ʈ
-+
Á˜
˯
--d
Ï
Ô
+
Ô
Ô
=
Ì
Ô
+
Ô
+=
Ô
Ó
15

Таким образом, ценность денег постоянно меняется во вре>
мени; 1 000 000 руб., выплаченный (не важно, нам или нами) се>
годня — это совсем не то же самое, что тот же 1 000 000 руб., вы>
плаченный через 10 лет. Сегодня этой суммой можно воспользо>
ваться (хотя бы для получения процентного дохода от вложения
на банковский счет), а десятилетний срок ожидания довольно>
таки долог. Если мы отложим использование данной суммы на 10
лет, и на этот срок положим ее в банк (который для определенно>
сти, платит 10% годовых), то через 10 лет у нас будет не
1 000 000
руб., а 1 000 000(1 + 0,10)
10
= 2 593 742 руб. 46 коп. — бо>
лее чем в 2,5 раза больше!
Поэтому сравнивать, складывать и производить любые
другие операции над денежными суммами можно только в том
случае, когда эти суммы рассматриваются в один и тот
же момент времени. При этом нужные операции необхо>
димо производить не над рассматриваемыми денежными сум>
мами, а над их современными эквивалентами.
В реальных условиях обычно используются схемы слож>
ных или непрерывных процентов; при этом сумма B
t
в момент
времени t > 0 имеет в момент времени t
0
= 0 ценность B
0
, опре>
деляемую соответствующей из формул (1.2.2) ~ (1.2.3). Если
t < 0,
то формулы (1.2.2) ~ (1.2.3) приведут просто к сумме B
0
,
накопленной за срок |
t
| = –t. Итак, вне зависимости от зна>
ка t ценность в настоящий момент времени суммы B
t
, выплачи>
ваемой в момент времени t, определяется формулами
(1.2.2) ~ (1.2.3). Эта ценность B
0
денежной суммы B
t
в настоящий
момент времени называется приведенной (или современной)
стоимостью суммы B
t
. Приведенная стоимость единичной
суммы обозначается v
t
; в случае сложных процентов
[{}]
[]
(1 )
nt
t
n
t
vi
ʈ
-+
Á˜
Ë
¯
=+ , (1.2.4)
а в случае непрерывного начисления процентов
v
t
= (1 + i)
–t
= e
–
d
t
. (1.2.5)
Всюду далее в этом пособии мы будем считать, что банк на>
числяет непрерывные проценты.
Величина
v = (1 + i)
–1
(1.2.6)
16

называется коэффициентом дисконтирования, при этом в
случае непрерывного начисления процентов из формулы (1.2.3)
следует, что
B
0
= B
t
v
t
.
Поскольку начальный момент времени может быть выбран
произвольно, ценность суммы в момент времени t
2
определя>
ется формулой
1
t
B
,
12
21
tt
tt
BBv
-
=
откуда
; (1.2.7)
1
12
t
tt
Bv Bv=
2
t
формула (1.2.7) выражает одинаковую ценность обеих сумм в
момент времени t
0
= 0.
ПРИМЕР 1.2.1. Что предпочтительнее: получить 10 000 че>
рез два года или 12 000 через три года, если банк начисляет
сложные проценты по ставке i = 10% годовых?
Решение. По формуле (1.2.4) приведенная стоимость первой суммы
равна
2
10000
(1 0,1)
=
+
8264 руб. 46 коп., а приведенная стоимость второй сум>
мы —
3
12000
(1 0,1)
=
+
9015 руб. 78 коп., поэтому второй вариант оказывается
предпочтительнее первого.
§ 1.3. ПОТОКИ ПЛАТЕЖЕЙ
Потоком платежей называется последовательность
(
)
(
)
(
)
(
)
01 2
012
;,;,;,,;,
n
tt t nt
tB tB tB tB……
, (1.3.1)
где t
k
— моменты времени,
k
— платежи, происходящие в со>
ответствующие моменты t
k
(k =0, 1, 2, … , n, …); поток платежей
может быть конечным (если последовательность (1.3.1) со>
стоит из конечного числа n платежей) или бесконечным
(
в противном случае).
t
B
Потоки платежей удобно изображать графически, при этом
положительные величины платежей, соответствующие денеж>
ным поступлениям, изображаются стрелками, направлен>
ными вверх, а отрицательные величины платежей, соответст>
вующие денежным выплатам, — стрелками, направленными
вниз (рис. 1.3.1).
ПРИМЕР 1.3.1. Предположим, что мы должны вернуть два
долга: 14 000 руб. через год и 6000 руб. через два года и хотим
17
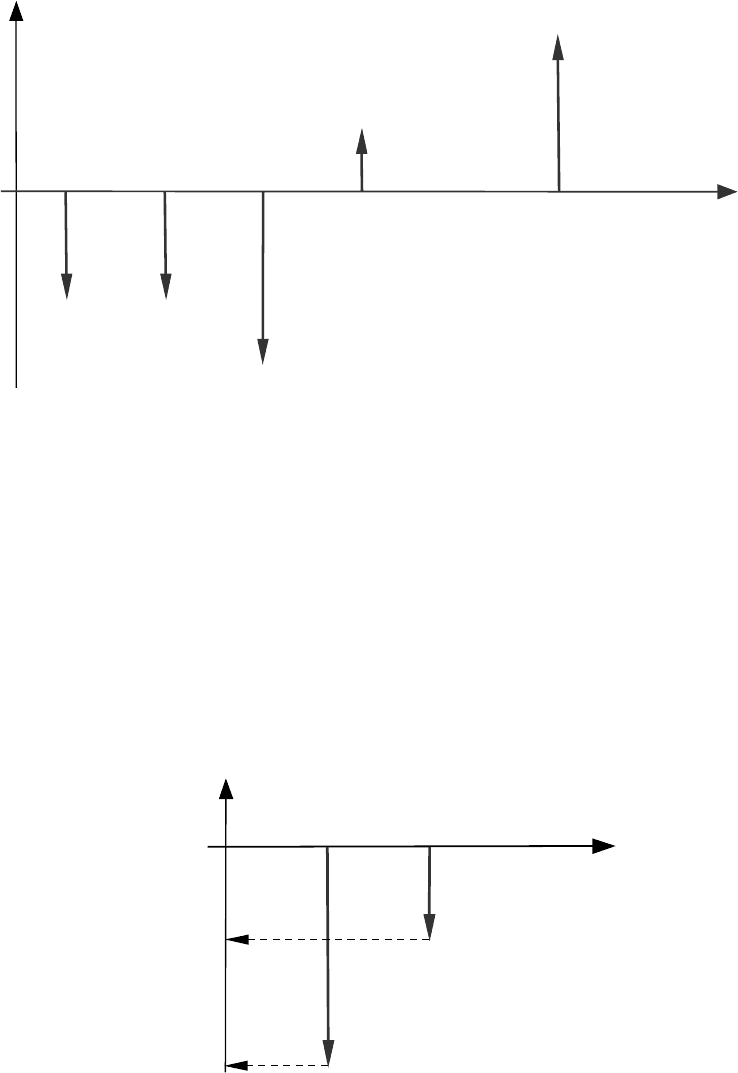
погасить свою задолженность досрочно, сегодня. Какую сумму
мы должны выплатить, если ставка банковского процента равна
i = 10%?
Решение. Поток платежей, соответствующий условиям данного при>
мера, изобразим на рис. 1.3.2.
t
0
t
1
t
2
t
3
··· t
n
···
0
t
B
1
t
B
B
t
t
3
t
B
n
t
B
0
2
t
B
Рис. 1.3.1. Поток платежей
Предположим, что кредитор предлагает нам просто осуществить се>
годня платеж, равный суммарному долгу: B
1
+ B
2
= –14 000 + (–6000) =
= –20 000 руб. Если бы мы сегодня поместили эту сумму x = 20 000 руб. в
банк, то через год она превратилась бы в x(1 + i) = 20 000(1 + 0,1) =
= 22 000 руб. Из этой суммы мы бы выплатили первый долг 10 000 руб., а
оставшиеся 22 000 – 10 000 = 12 000 руб. оставили бы на банковском счете,
тогда еще через год на счете будет 12 000(1 + 0,1) = 13 200 руб., из кото>
рых мы заплатим долг 6000 руб., при этом у нас на счете останется
13 200 – 6000 = 7 200 руб. Видно, что согласившись выплатить просто
сумму долгов, мы существенно переплатили бы!
0 1 2
B
1
= –14 000
B
2
= –6 000
B
t
t
–12 727,27
–4958,68
Рис. 1.3.2. Поток платежей в примере 1.3.1
Найдем теперь справедливый размер x нашей сегодняшней выпла>
ты. Через год сумма x превратится в x(1 + i), и из этой суммы мы выпла>
тим первый долг B
1
= –14 000 руб. Остаток x(1 + i) + B
1
еще через год пре>
вратится в (x(1 + i) + B
1
)(1 + i) = x(1 + i)
2
+ B
1
(1 + i), из которых мы вы>
18

платим второй долг B
2
= –6000 руб., после чего на счете останется
x(1 + i)
2
+ + B
1
(1 + i) +B
2
. Если этот остаток будет положителен, то такая
операция несправедлива по отношению к должнику, а если он будет от>
рицателен — то по отношению к кредитору. Таким образом, справедли>
вая сумма x должна определяться из условия x(1 + i)
2
+ B
1
(1 + i) +B
2
= 0,
что дает
x = –(B
1
(1 + i)
–1
+ B
2
(1 + i)
–2
).
В нашем примере
12
22
14000 14000
6000 6000
1(1) 10,1(10,1) 1,11,21
12727,27 4958,68 17685,95 руб. 17685 руб.95 коп.;
BB
x
ii
-
-
ʈʈ
=- + =- + = + =
Á˜Á ˜
Ë¯Ë ¯
++ + +
=+= =
при этом первое слагаемое 12 727 руб. 27 коп. — это абсолютная величина
современной стоимости первого долга, а 4958 руб. 68 коп. — абсолютная
величина современной стоимости второго долга.
Пример 1.3.1 демонстрирует, что для того, чтобы оценить со>
временную стоимость потока платежей, необходимо все эти пла>
тежи привести по формуле (1.2.3) к начальному моменту време>
ни, после чего сложить полученные приведенные стоимости пла>
тежей. Можно обобщить этот результат и рассматривать стои>
мость потока платежей не только в настоящий момент времени,
но и в любой другой момент T: стоимостью потока платежей
(1.3.1)
в момент времени T называется сумма платежей, дискон>
тированных (приведенных) к этому моменту:
, (1.3.2)
() (1 )
k
k
Tt
t
k
BT B i
-
=+
Â
при этом величина
(1.3.3)
(0) (1 )
k
k
t
t
BBi
-
== +
Â
NPV
k
называется современной стоимостью потока платежей (1.3.1)
или его чистым приведенным доходом (Net Present Value), а
величина
(1.3.4) () (1 )
nk
k
tt
nt
Bt B i
-
== +
Â
NFV
n
1
k
=
называется накопленной стоимостью потока платежей (1.3.1)
к моменту t
n
или его чистым накопленным доходом к моменту
t
n
(Net Future Value); обычно рассматривают накопленную стои>
мость потока платежей к моменту последнего платежа.
В пакете Microsoft Excel существует функция
NPV = ЧИСТНЗ(<i>; <массив >; <массив t
k
>)
k
t
B
для вычисления современной стоимости потока платежей.
19
§ 1.4. РЕНТЫ
Рентой называется право на получение одинакового пла>
тежа C с одинаковой периодичностью; иными словами, рента —
это поток одинаковых платежей с одинаковыми промежутками
между платежами. Ограниченной рентой или аннуитетом
называется рента, состоящая из конечного числа n одина>
ковых платежей C, выплачиваемых с одинаковой периодично>
стью, если платежи ренты никогда не заканчиваются, то такая
рента называется вечной. Если платежи ренты производятся
строго в конце года, такая рента называется годовой, иначе —
общей. Если платежи производятся в конце каждого периода,
то такая рента называется запаздывающей, а если в начале ка>
ждого периода — то упреждающей.
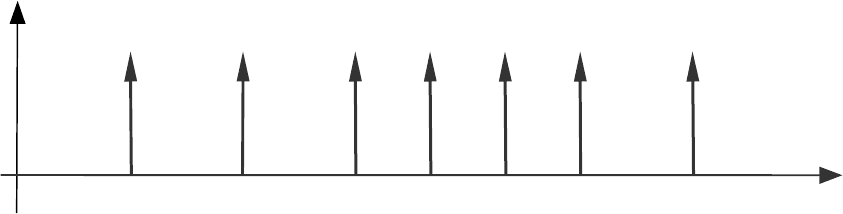
Вначале рассмотрим ограниченную запазды>
вающую годовую ренту. Пусть i — годовая процентная
ставка. Поток платежей, соответствующий этой ренте, пред>
ставлен на рис. 1.4.1.
Современная стоимость такого потока платежей по форму>
ле (1.4.3) равна
(
)
(
)
11 1
123 (1)
(0) (1) (1) (1)
(1 ) (1 ) (1 ) (1 ) (1 )
nn n
kk
k
kk k
nn
BBi CiCi
Ci i i i i
--
== =
--- -- -
= = += + = +=
= + ++ ++ + ++ ++
ÂÂ Â
NPV
k-
или, с учетом обозначения (1.2.6),
.
23 1
()
nn
Cv v v v v
-
=+++++NPV
B
1
=
C B
2
=
C B
3
=
C ··· B
n
– 1
=
C B
n
=
C
···
0 1 2 3
n
–1
n
B
t
t
Рис. 1.4.1.
Поток платежей, соответствующий ограниченной годовой ренте
В скобках стоит сумма первых n членов геометрической
прогрессии с первым членом b
1
= v и знаменателем q = v, эта
сумма равна
20
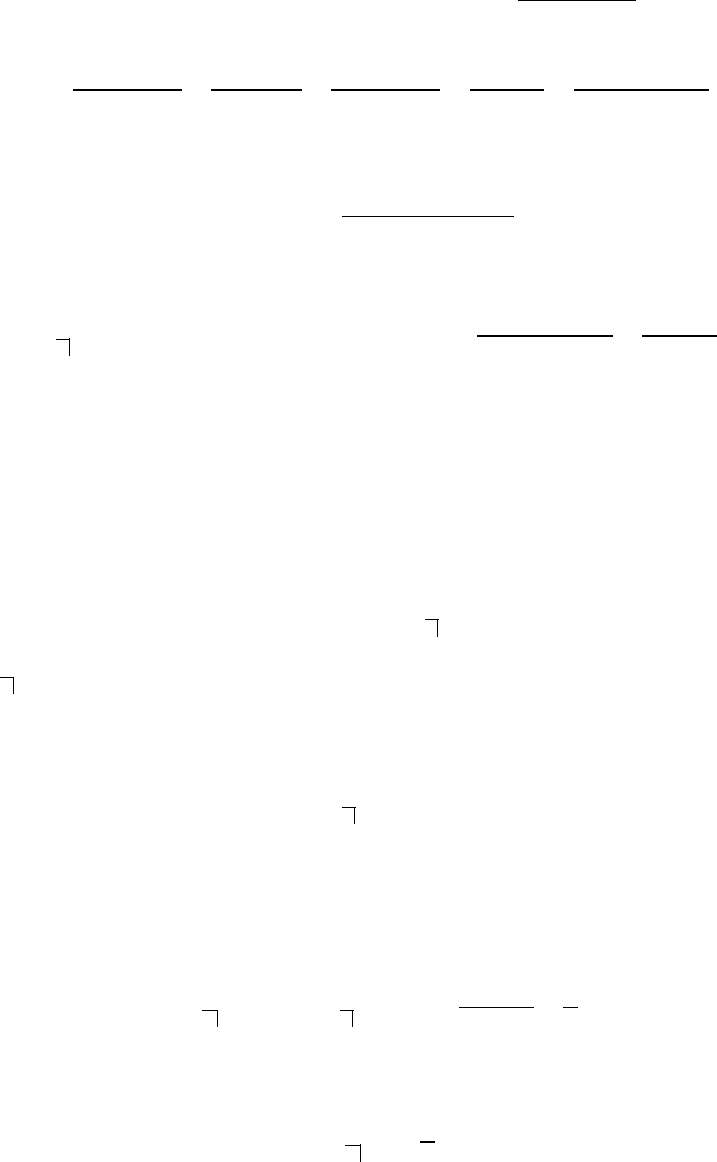
1
23 1
(1 )
1
(1 ) 1 1 1 1 (1 )
,
11/1(1)1
n
nn
n
nn nn
bq
vv v v v S
q
vv v v v i
vv i i i
-
-
-
++++ += = =
-
-- ---+
=====
--+-
n
поэтому
(1 (1 ) )
n
Ci
i
-
-+
=
NPV . (1.4.1)
Величина
23 1
@
1(1 ) 1
nn
nn
ni
iv
avvv vv
ii
-
-
-+ -
=+ + + + + = =
, (1.4.2)
равная приведенной стоимости годовой ограниченной запазды>
вающей ренты, состоящей из n единичных платежей, называет>
ся коэффициентом приведения такой ренты.
Таким образом, современная стоимость годовой ограничен>
ной запаздывающей ренты, состоящей из n платежей в сумме C
каждый, равна
@ni
Ca=NPV , (1.4.3)
где
@ni
a определяется формулой (1.4.2).
При i = 0 формула (1.4.2) неверна, однако непосредственный
подсчет показывает, что
@0n
an= .
При увеличении срока ренты (при n Æ •) коэффициент
приведения годовой ограниченной запаздывающей ренты стре>
мится к пределу
@@
11
lim lim
n
ini
nn
v
aa
ii
•
Æ• Æ•
-
== =
(
поскольку v = (1 + i)
–1
< 1); этот предел
@
1
i
a
i
•
=
представляет собой коэффициент приведения годовой веч>
ной запаздывающей ренты.
Если в качестве нулевого момента времени выбрать момент
первого платежа запаздывающей ренты, то такая запаздываю>
щая рента может рассматриваться как упреждающая, поэтому
21
