Соловьев В.И. Математические методы управления рисками
Подождите немного. Документ загружается.


Отметим, что любой портфель p (3.3.1) можно представить в
виде
, (3.3.4)
0
(1 )xx=+-ep
0
y
где
e = (1, 0, 0, …, 0) —
безрисковый портфель, совпадающий с банковским счетом,
12
00
0, , , ,
11 1
n
x
xx
xx x
0
ʈ
=
Á˜
-- -
˯
y …
—
чисто рисковый портфель, не содержащий безрисковых вло>
жений.
Рассмотрим вначале чисто рисковый портфель
,
12
(0, , )xx=y
состоящий из двух акций с ожидаемыми эффективностями
r
1
= ME
1
и r
2
= ME
2
, рисками s
1
и s
2
и ковариацией s
12
= cov(E
1
; E
2
).
Поскольку x
1
+ x
2
= 1, то можно ввести обозначение x = x
1
,
при этом x
2
= 1 – x
1
= 1 – x, и тогда эффективность такого
портфеля можно выразить как
,
11 22 1 2
(1 )ExExExE xE=+=+-
y
ее математическое ожидание
,
11 22 1 2 1 2
()(1) (ExExExE xErxr=+=+-=+
y
MM M M 1)x-
)=
дисперсия
(3.3.5)
,
22
11 22 1 1 2 2 12 1 2
() 2cov(;E xExE xExE xx EE=+=++
y
DD D D
22 2 2
12 12
(1 ) 2 (1 )xxxx=s+- s+ -s
а задача (3.3.3) для этого портфеля будет иметь вид
,
22 22
12 12
(1 ) 2 (1 ) minxxxxs+ - s+ - s Æ
12
(1 ) , .rx r x r x+-= Œ
R
p
Уравнение говорит о том, что каждой вы>
бранной инвестором ожидаемой эффективности портфеля
будет соответствовать ровно одно значение переменной x:
12
(1 )rx r x r+-=
p
r
p
2
12
rr
x
rr
-
=
-
p
,
62
а значит, ровно один портфель
22 2
12 12 1221
0, ,1 0, ,
rr rr rrrr
rr rr rrrr
-- --
1
ʈÊ
ˆ
=-=
Á˜Á
-- --
˜
˯Ë
¯
y
pp pp
, (3.3.6)
при этом дисперсия эффективности этого портфеля будет за>
висеть от его ожидаемой эффективности по формуле
(3.3.7)
22 2 2
12
(1 ) 2 (1 )Ex x x x=s+- s+ -s=
y
D
12
()()
22
22
2112
12
2
12 21 12
22
21 12 12 1
2
12
()(
2
()
() () 2()
()
rr rr rr
rr rr rr
rr rr rr
rr
--s-
ʈʈ
=s+s-
Á˜Á˜
--
˯˯
-s+ -s -s -
-
pp p
pp p
1
2
)
(
.
rr
rr
-
-
=
p
p
2
)
-
=
Рассмотрим два частных случая.
Пусть вначале акции абсолютно коррелированы,
т. е. r(E
1
; E
2
) = ±1, откуда с учетом определения коэффициента
корреляции
12
12
12
cov( ; )
(; )
EE
EEr=
ss
получаем, что s
12
= cov(E
1
; E
2
) =
= ±s
1
s
2
.
В этом случае по формуле (3.3.7)
(
)
(
)
(
)
(
)
()
22
21 12 21 12
2
12
2
21 12
2
12
() () 2()()
()
()()
()
rr rr rr rr
E
rr
rr rr
rr
-s+ -s -s -s
==
-
-s -s
=
-
y
D
∓
∓
pp pp
pp
(
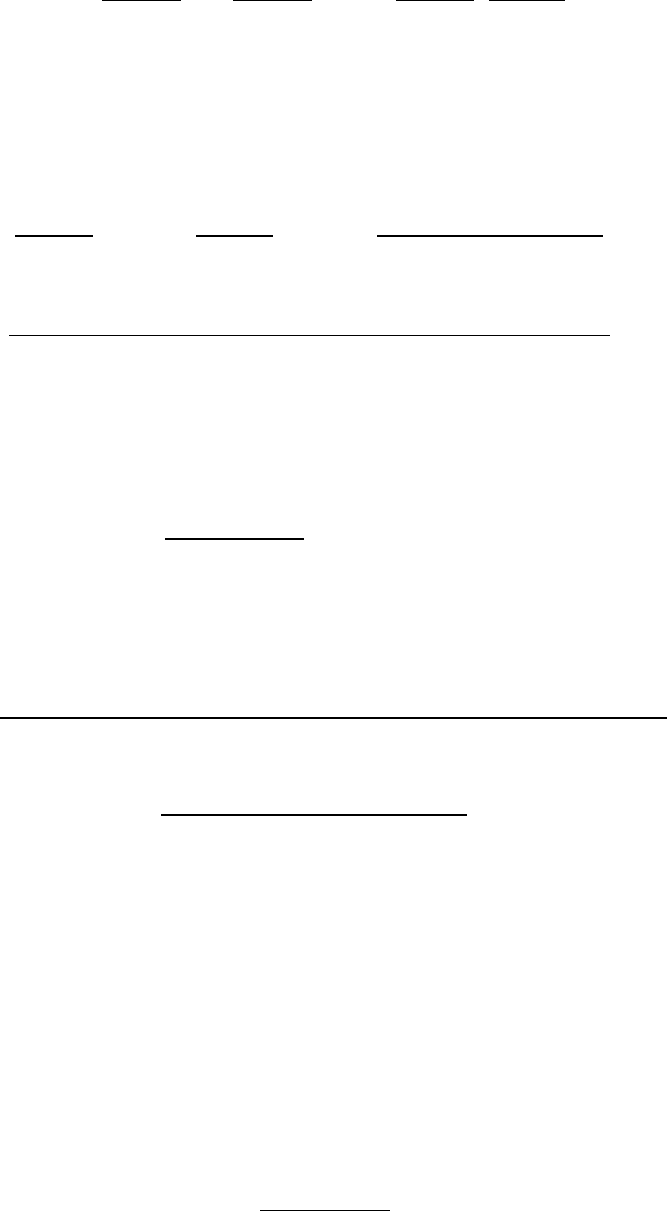
график зависимости DE
y
от при r
12
= ±1 и различных соот>
ношениях между r
1
, r
2
, s
1
и s
2
представлен на рис. 3.3.1, а ~ г), по>
этому инвестор можно выбрать ожидаемую эффективность
портфеля так, чтобы числитель в последнем выражении об>
ратился в нуль, т. е.
r
p
r
p
21 12
()()rr rr-s -s=
∓
pp
0
или
21 12
12
rr
r
*
ss
=
ss
∓
∓
p
,
при этом дисперсия портфеля (а значит, и его риск) обратится
в нуль!
63
D
E
y
2
2
s
2
1
s
r
p
0
r
*
p
r
1
r
2
а) r
12
= 1, r
1
< r
2
, s
1
< s
2
, r
2
/ r
1
< s
2
/ s
1
D
E
y
2
2
s
2
1
s
r
*
p
0
r
1
r
2
r
p
~
б) r
12
= 1, r
1
< r
2
, s
1
< s
2
, r
2
/ r
1
> s
2
/ s
1
D
E
y
2
1
s
2
2
s
0
r
1
r
2
r
*
p
r
p
~
в) r
12
= 1, r
1
< r
2
, s
1
> s
2
DE
y
2
1
s
2
2
s
0
r
1
r
*
p
r
2
r
p
~
г) r
12
= –1
D
E
y
2
2
s
2
1
s
0
r
1
r
*
p
r
2
2
*
s
y
r
p
~
д) r
12
π ±1
Рис. 3.3.1.
Зависимость дисперсии портфеля от его ожидаемой эффективности
64

В соответствии с (3.3.8) такой портфель нулевого риска бу>
дет задан вектором
21 12 21 12
21
12 12 2 1
12 21 2 11 2
0, , 0, ,
rr rr
rr
rr rr
*
ss ss
ʈ
--
Á˜
ss ss s s
ʈ
==
Á˜
Á˜
--ssss
˯Ë
¯
y
∓∓
∓∓
∓∓
.
Отметим, что выбор портфеля нулевого риска не всегда бы>
вает оправдан. Действительно, если r
12
= 1, r
1
< r
2
, s
1
< s
2
,
r
2
/ r
1
< s
2
/ s
1
, то несмотря на нулевой риск, такой портфель
имеет эффективность ниже, чем каждая из ожидаемых эффек>
тивностей акций r
1
и r
2
(см. рис. 3.3.1, а), а в случае, когда r
12
= 1,
r
1
< r
2
, s
1
< s
2
, r
2
/ r
1
> s
2
/ s
1
, портфель нулевого риска будет во>
обще иметь отрицательную эффективность (см. рис. 3.3.1, б) —
составив такой портфель, мы гарантированно окажемся в
убытке!
Пусть теперь акции абсолютно некоррелированы,
т. е. r(E
1
; E
2
) = 0, откуда s
12
= 0.
В этом случае дисперсия портфеля по формуле (3.3.5) равна
(3.3.8)
.
22 2 2
12
(1 ) 2 (1 )Ex x x x=s+- s+ -s=
y
D
22 2 2 2 2 2 2
1212
(1 ) ( ) 2xx xxs+ - s=s+s - s+
12
2
2
2
= s
Формула (3.3.8) задает квадратичную функцию от x, гра>
фик которой представляет собой параболу с ветвями, направ>
ленными вверх, и вершиной в точке минимума
22
21
22 22
12 12
;xE
*
*
2
2
ʈ
ss
==
Á˜
s+s s+s
s
˯
y
D .
Такой портфель y
*
, обеспечивающий минимальный риск
12
12
22
12
min{ ; }
*
ss
s= < ss
s+s
y
,
задается вектором
22
21
2222
1212
0, ,
*
ʈ
ss
=
Á˜
s+s s+s
˯
y ,
а его эффективность равна
[]
22
12 21
12 12
22
12
min{ ; }; max{ ; }
rr
Err
*
s+ s
=Œ
s+s
p
rr.
65
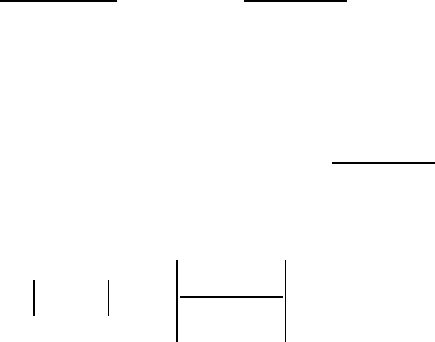
График зависимости DE
y
от при r
12
= 0 представлен на
рис. 3.3.1, д.
r
p
В общем случае зависимость дисперсии портфеля от его
ожидаемой эффективности описывается формулой (3.3.7), гра>
фик такой зависимости при произвольном r(E
1
; E
2
) π ±1 пред>
ставляет собой параболу, как и на рис. 3.3.1, д.
Теперь учтем возможность безрисковых вложений и заим>
ствований.
Вспомним, что согласно формуле (3.3.4) любой портфель p
может быть представлен в виде
,
00
(1 )xx=+-eyp
где y — некоторый чисто рисковый портфель.
При этом
,
00 0 0 0 0 0 0
( (1)) (1) (1ExE xExE xEixE=+-=+-=+-
yy
MM M M M
p
)x
y
E
и если задано требуемое значение ожидаемой эффективности
портфеля r , то = M
pp
00
,1 ,
Er
ri
xx
Ei Ei
-
-
=-=
--
y
yy
M
MM
p
p
поэтому
2
2
00 0 0
((1))(1)
ri
ExE xE xE
Ei
-
ʈ
=+-=- =
Á˜
-
˯
yy
y
DD D D
M
p
p
E
y
.
откуда
0
1
ri
x
Ei
-
s= - s= s
-
yy
y
M
p
p
.
Зависимость s
p
от при различных значениях r
12
будет
изменяться от прямой, проходящей через точки (r
1
; s
1
) и (r
2
; s
2
)
[
при r(E
1
; E
2
) = 1] до ломаной, проходящей через точки (r
1
; s
1
),
( ; 0) и (r
2
; s
2
) [при r(E
1
; E
2
) = –1]; в общем случае [при произ>
вольном r(E
1
; E
2
) π ±1] такой график представляет собой гипер>
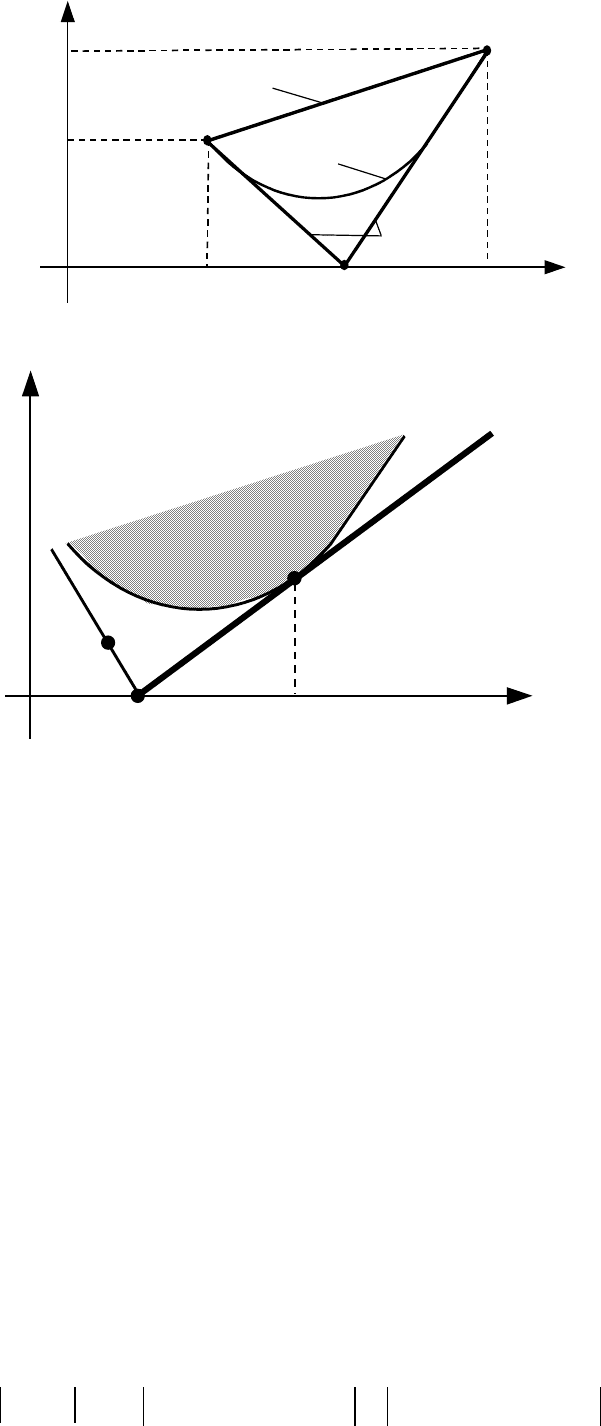
болу (рис. 3.3.2, а).
r
p
E
*
p
На рис. 3.3.2, б заштрихованы все возможные варианты риско>
вых портфелей, составленных из двух акций. На том же графике
отметим точку (i; 0), соответствующую безрисковому портфелю
e = (1, 0, 0).
66
s
2
s
1
r
0
r
1
r
*
p
r
2
s
p
r
= –1
r
= 1
r
π
±
1
а) зависимость риска от ожидаемой эффективности при различных r
s
p
r
p
0
i
M
r
*
C
(p
M
)
B
(e)
A
(p
0
)
б) множество портфелей с безрисковой составляющей
Рис. 3.3.2. Определение рыночного портфеля
Будем теперь составлять портфель , обес>
печивающий данный уровень эффективности .
0
(1 )xx=+-eyp
r
p
0
0
y
y
Его рисковую составляющую мы можем выбрать
произвольно из заштрихованной области, а безрисковая
составляющая портфеля фиксирована: это портфель e,
соответствующий точке (i; 0).
При произвольном выборе рисковой составляющей y порт>
фель будет представлять собой выпуклую
комбинацию точки e и точки y, т. е. будет лежать на пря>
мой, соединяющей эти точки. Множество всех таких прямых
соответствует области внутри угла ABC на рис. 3.3.2, б (так как
эффективность
0
(1 )xx=+-ep
00 0 0
(1 ) (1 )xi x E xm x m+- = +-
ye
M
портфеля p будет представлять собой выпуклую комбинацию
эффективностей портфелей e и y, а риск
00 0 0 0
10(1)(1xx x x xs= - s= ◊+ - s = s+ - s
yyep
)
y
67

портфеля p будет равен абсолютному значению выпуклой ком>
бинации рисков портфелей e и y). Правая граница этого множест>
ва (выделенная на рис. 3.3.2, б жирной линией и соответствующая
портфелям, оптимальным по Парето) проходит, очевидно, через
точку B(e) и касается заштрихованной области в некоторой точке
C(p
M
). Портфель y = p
M
, соответствующий точке касания, называ>
ется рыночным (или касательным) портфелем.
Выбирать портфель p мы будем, конечно же, из множества
портфелей, оптимальных по Парето (т. е. как выпуклую комби>
нацию безрискового актива и рыночного
портфеля); этому множеству соответствует жирная линия BC
на рис. 3.3.2, б, которая называется линией рынка капитала
(Capital Market Line).
Каждому заданному значению бу>
дет соответствовать свой оптимальный портфель p, со>
ответствующий минимальному значению риска s
00
(1 )
M
xx=+-ep
rr
*
=
pp
p
ir
p
p
p
, которого мож>
но достичь с использованием безрисковых вложений и заимство>
ваний. Видно, что при всех риск оказывается ниже, чем у
чисто рискового портфеля y с той же ожидаемой эффективно>
стью (при портфель p будет целиком состоять из акций,
просто совпадая с чисто рисковым портфелем y).
rr
*
π
p
В общем случае (при произвольном количестве акций в
портфеле) аналитическое решение задачи (3.3.2) описывается
формулами
1
0
T1
1
(), 1
() ()
n
k
k
ri
x
*-*
-
=
-
=-
--
Â
xri
ri ri
p
S
S
x
*
=-
1
2
nn
, (3.3.9)
где
11112
1
22122
2
12
,,,
n
n
nnn
n
ri
x
ri
x
ri
x
*
*
*
*
ss s
ʈ
ʈ ʈ Ê ˆ
Á˜
Á˜ Á˜ Á ˜
ss s
Á˜
Á˜ Á˜ Á ˜
===
Á˜
Á˜ Á˜ Á ˜
Á˜
Á˜ Á˜ Á ˜
ss s
˯ ˯ Ë ¯
˯
xri
S=
,
а риск такого оптимального портфеля подчиняется формуле
T1
() ()
ri
*
-
-
s=
--ri ri
p
p
S
, (3.3.10)
из которой видно, что зависимость риска оптимального портфе>
ля от эффективности этого портфеля является линейной.
*
s
p
r
p
68
Доказательство формул (3.3.9) ~ (3.3.10) довольно громозд>
кое, его можно найти, например, в книге [36], но в практической

работе гораздо проще воспользоваться инструментом «Поиск
решения
» пакета Microsoft Excel.
ПРИМЕР 3.3.1. С каким наименьшим риском можно дос>
тичь 20%>ной эффективности инвестиций, если есть возмож>
ность банковских вложений и заимствований по ставке i = 10%
годовых, а на рынке ценных бумаг обращаются две акции, их
ожидаемые эффективности равны соответственно r
1
= 16% и
r
2
= 23%, риски s
1
= 5%, s
2
= 14%, а коэффициент корреляции
доходностей данных акций равен r
12
= 0,36?
Решение. Введем данные в рабочий лист Microsoft Excel, как показано
на рис. 3.3.3, а. Пусть ячейки B9 и B10 соответствуют долям рисковых
вложений x
1
и x
2
, в ячейку B8, соответствующую доле безрисковых вло>
жений x
0
, введем формулу, соответствующую разности всех вложений
(единицы) и вложений в акции x
1
и x
2
, в ячейку B12 введем формулу для
ожидаемой эффективности портфеля ME
p
, а в ячейку B13 введем форму>
лу для дисперсии эффективности портфеля DE
p
; учтем здесь, что s
12
=
= r
12
s
1
s
2
(эти формулы приводятся справа от соответствующих ячеек).
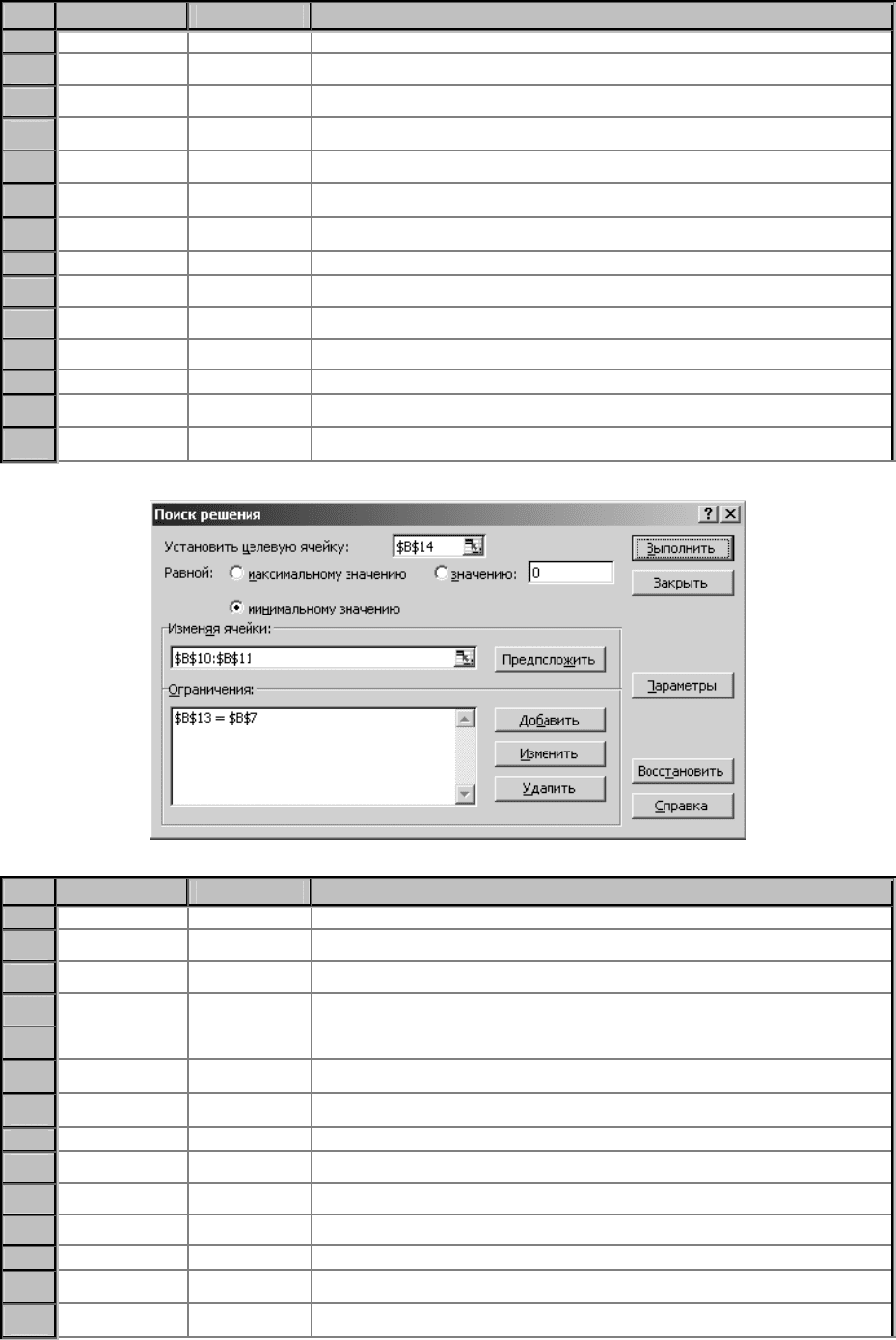
Воспользуемся инструментом «Поиск решения». Для этого выберем в
меню «Сервис» пункт «Сервис | Поиск решения…», и в появившемся окне
(рис. 3.3.3, б) укажем, что мы хотим установить целевую ячейку $B$14 (в
которой рассчитывается дисперсия портфеля) равной минимальному
значению, изменяя ячейки $B$10:$B$11 (в которых находятся доли рис>
ковых составляющих портфеля), причем в задаче присутствует ограни>
чение $B$13 = $B$7. После нажатия на кнопку «Выполнить» в рабочем лис>
те произойдут изменения: в ячейках B9, B10 и B11 появятся значения
, в ячейке B13 будет рассчитана ожи>
даемая эффективность портфеля (она равна требуемой эффективности
, а в ячейке B14 появится рассчитанное значение дисперсии эф>
фективности портфеля DE
p
= 0,0058. При этом риск портфеля равен
012
0,3908, 1,1543, 0,2365xxx
***
=- = =
0,20r =
p
0,0058 0,076 7,6%s= ª =
p
12
0,3908, 1,1543, 0,2365xx
**
=- = =
. Интерпретация оптимального решения
такова: необходимо 23,65% потратить на
приобретение акций второго вида, взять банковский кредит в размере
39,08% от общей суммы собственных средств, после чего все оставшиеся
после покупки акций второго вида собственные средства вместе со сред>
ствами, полученными в кредит, вложить в покупку акций первого вида.
Результаты работы программы представлены на рис. 3.3.3, в.
0
x
*
=
М н о ж и т е л ь Л а г р а н ж а, который приводится в «Отчете по ус!
тойчивости», равен l = 0,116; это означает, что увеличение эффективно>
сти
заданного портфеля на 1% приведет к тому, что риск оптимального
портфеля, обладающего такой эффективностью, увеличится приблизи>
тельно на
r
p
0,1161 0,341%ª .
69
A B С
1 i = 0,10
2
r
1
= 0,16
3
r
2
= 0,23
4
s
1
=
0,05
5
s
2
=
0,14
6
r
12
=
0,36
7
r
p
=
0,20
8
9
x
0
= 1,00
=1!B10!B11
10
x
1
=
11
x
2
=
12
13
ME
p
=
0,10
=B9*B1+B10*B2+B11*B3
14
DE
p
=
0,00
=B10^2*B4^2+B11^2*B5^2+2*B10*B11*B6*B4*B5
а) ввод исходных данных
б) окно «Поиск решения»
A B С
1 i = 0,10
2
r
1
= 0,16
3
r
2
= 0,23
4
s
1
=
0,05
5
s
2
=
0,14
6
r
12
=
0,36
7
r
p
=
0,20
8
9
x
0
= –0,3908
=1!B10!B11
10
x
1
= 1,1543
11
x
2
= 0,2365
12
13
ME
p
=
0,2000
=B9*B1+B10*B2+B11*B3
14
DE
p
=
0,0058
=B10^2*B4^2+B11^2*B5^2+2*B10*B11*B6*B4*B5
в) результаты
Рис. 3.3.3. Расчеты в примере 3.3.1
70

Можно поставить и другую задачу — задачу максими>
зации ожидаемой эффективности портфеля при
заданном максимальном допустимом риске : s
p
, (3.3.11)
0
1
min
n
kk
k
xi xE
=
ʈ
+Æ
Á˜
˯
Â
M
0
1
0
1
,
1,
(0,1,2,,
n
kk
k
n
k
k
k
xi xE
xx
xk
=
=
ʈ
+=
Á˜
˯
+=
Œ=
Â
Â
D
…
p
R
).n
s
Задачи (3.3.2) и (3.3.11) были поставлены и успешно решены
Г. Марковицем [24] в 1952 г. для частного случая отсутствия без>
рискового актива (x
0
= 0) и обобщены Дж. Тобином [38],
У. Шарпом [43], Дж. Линтнером [22] и др. Дж. Тобин стал лауреа>
том Нобелевской премии в области экономики в 1981 г., Г. Марко>
виц и У. Шарп стали Нобелевскими лауреатами в 1990 г.
Осталось отметить, что реальные инвесторы, обладая ин>
формацией об оптимальных портфелях, как правило, прини>
мают решения о составлении портфелей акций, исходя из соб>
ственной интуиции; решения эти в большинстве случаев прино>
сят больше дохода, чем если бы инвесторы строили оптималь>
ные портфели по схеме, рассмотренной в этом параграфе.
3.3.2.
Модель оценки основных активов
Для построении оптимального портфеля необходимо знание
математических ожиданий и взаимных ковариаций эффектив>
ностей акций. Для этого, казалось бы, можно воспользоваться
прямым статистическим подходом: поскольку данные о коти>
ровках акций на торговых площадках доступны в сети Интер>
нет, можно в качестве оценок математических ожиданий ME
k
,
волатильностей s
k
и ковариаций cov (E
k
; E
j
)взять их выборочные
аналоги — соответственно
1
T
kt
t
k
e
e
T
=
=
Â
,
2
1
()
T
kt k
t
k
ee
T
=
-
s=
Â
ˆ
,
1
()(
v( ; )
T
kt jt
t
kj
eeee
EE
T
=
--
=
Â
)
co
,
где e
kt
— эффективность акции с номером k в день с номером t.
Но не так все просто!
71
