Солодов В.Г. Моделирование турбулентных течений. Расчет больших вихрей
Подождите немного. Документ загружается.


71
v
T
j i ij
j j j
ˆ
ˆ
E q
ˆ
ˆ
u E p u
t x x x
j j j j ij j
j j j i
u u p u p u u
x x x x
v v v
i i i
ij ij v ij ij i ij i T T
j j j i i
u u u
ˆ ˆ
u u q q
x x x x x
Здесь величины
v
ij
ˆ
и
T
ˆ
q
- суть вязкие напряжения и тепловой
поток, которые вычисляются по разрешаемым переменным. Они
равны фильтрованным величинам в случае постоянных значений
вязкости и теплопроводности среды. Величина
ij i j i j
u u u u
является невязкой между фильтрованным произведением скоростей и
составленным из фильтрованных по Фавру разрешаемых величин.
Уравнение переноса пассивного скаляра
- параметра, не
взаимодействующего с другими полями параметров, представляется в
виде
j
j j j
u F
t x x x
,
где неизвестные корреляционные моменты
i j
u u
,
j
u
должны
моделироваться специальным образом по аналогии с методом,
описанным выше.
Отфильтрованный тензор скоростей деформаций определяется
как
1
2
j
i
ij
j i
u
u
S
x x
.
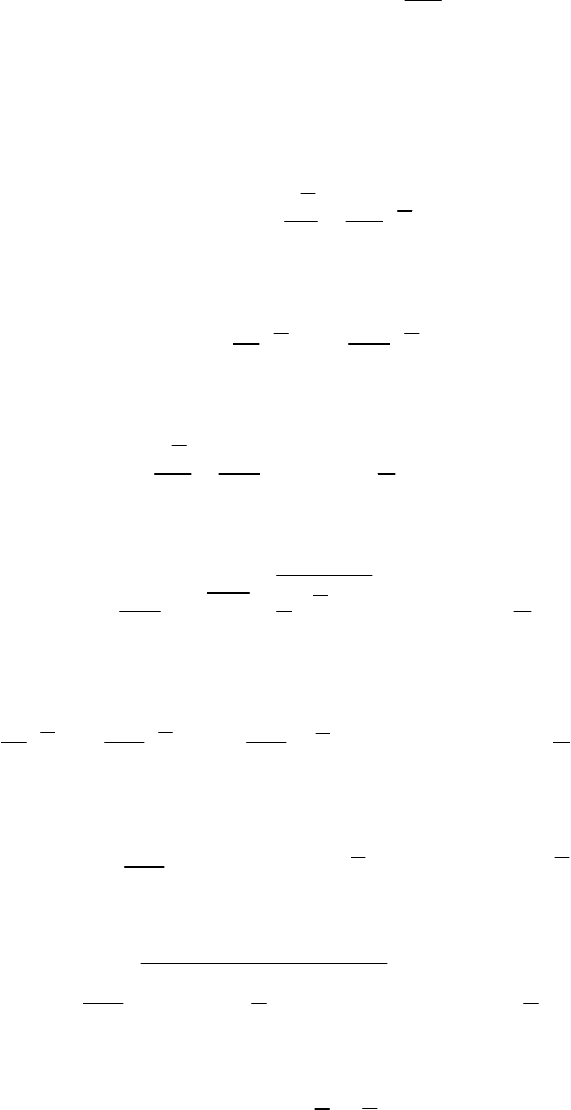
72
Величина
означает коэффициент молекулярного переноса скаляра
. Величина
F
- мощность источника величины
.
По аналогии с гипотезой Буссинеска для турбулентного
переноса импульса можно формально ввести коэффициент
турбулентного переноса величины
i
i
u
x
Приведем еще одну форму уравнения FNS в декартовой системе
с осреднением по Фавру [140]
i
i
u
t x
i i j
j
u u u
t x
2
2
3
ij
F SGS
ij kk ij
i j
p
S S
x x
1 2
2 2
3 3
ij kk ij ij kk ij
j
S S S S
x
,
2
2
3
j kk ij B kk ij ij
j j
q
e u e pS S S S
t x x
j j j j kk
kk
j
u e u e q q pS pS
x
1 1
2 2
3 3
ij kk ij ij ij kk ij ij
j
S S S S S S
x
R
p T
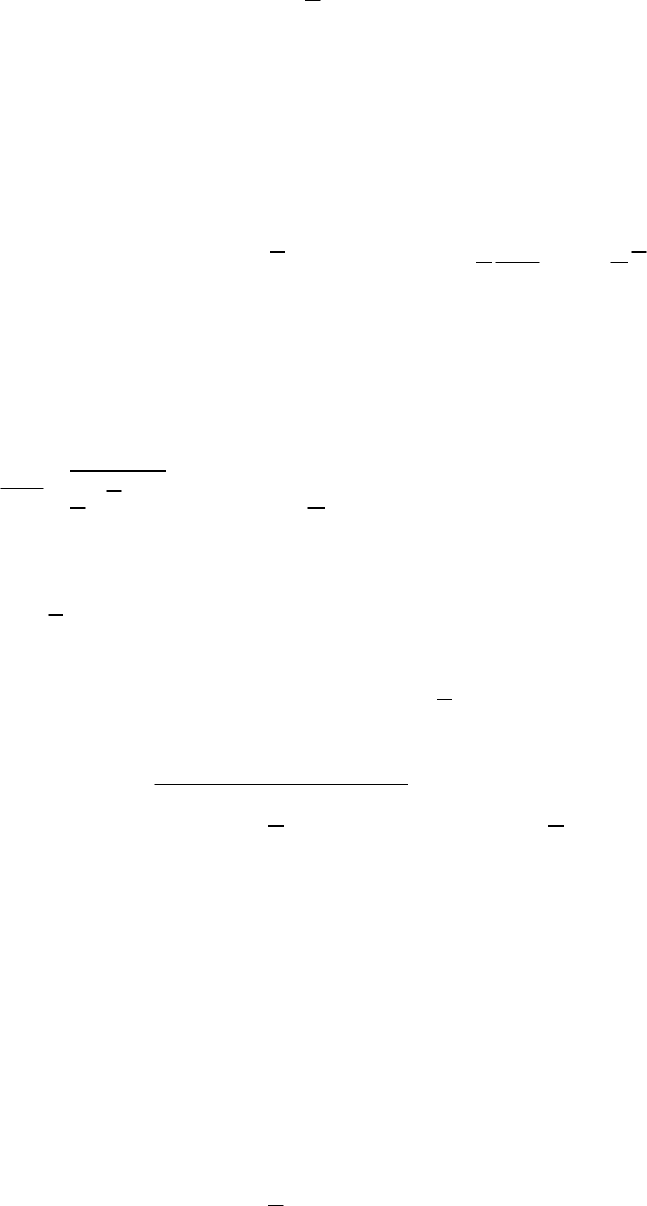
73
Величина
F SGS
ij i j
u u
подобна рейнольдсовому аналогу, и
также является симметричным тензором подсеточных турбулентных
напряжений, и требует способа определения.
В соответствии с гипотезой Буссинеска о вихревой вязкости
можно записать
1 2
2
3 3
F SGS
k
ij i j T ij ij ij
k
u
u u S K
x
В уравнениях
e
обозначает внутреннюю энергию,
ij
S
-
фильтрованный по Фавру тензор скоростей деформаций. Среди
моделируемых членов уравнений разностью
1 2
2 2
3 3
ij kk ij ij kk ij
S S S S
обычно пренебрегают; в уравнении
энергии разность выражается через подсеточные напряжения [190],
член
j j
q q
может быть опущен, величины
kk
kk
pS pS
и
1 1
2 2
3 3
ij kk ij ij ij kk ij ij
S S S S S S
являются предметом моделирования [190].
3.7 Проблема коммутации фильтров
В общем случае операция фильтрования случайной величины
1 2 3
x ,x ,x
[105] представляется в виде (см. также [219])
x G x, d
,
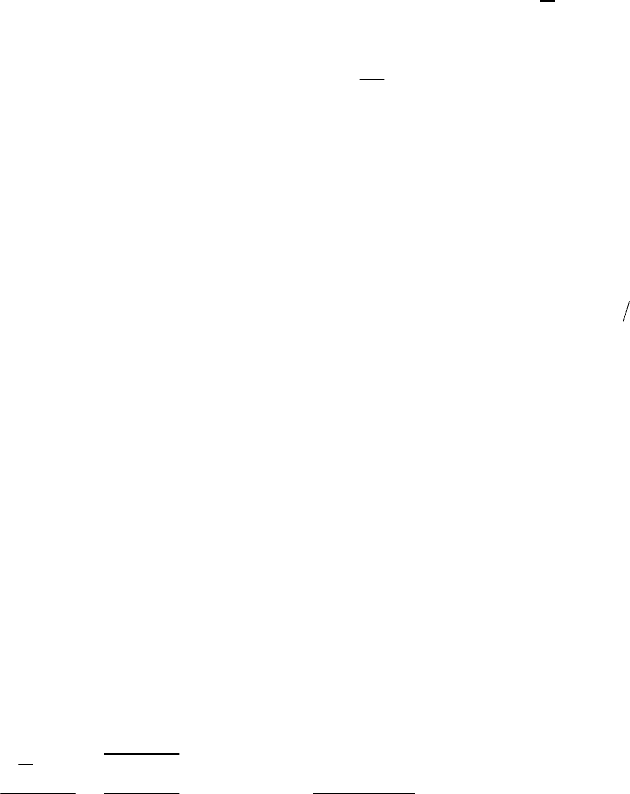
74
где концепция фильтра распространена на трехмерную область с
1 2 3 1 2 3
, , , , ,
x x x x
. Свойство функции фильтра, применяемого
к константе
1
G x, dx d
.
Разложение с участием фильтрующей операции кажется
похожим на рейнольдсово разложение, однако величина
является
случайной именно ввиду узости фильтра, и применение фильтра к
подсеточной величине
не равно нулю
0
, хотя, переходя к
пределу по ширине фильтра, мы получаем нуль.
В большинстве интересных задач уравнения FNS интегрируются
на однородных, но анизотропных сетках
i
h
,
1,2,3
i
, и в этом случае
вынужденно используется анизотропный фильтр
i
. При этом
характерный размер фильтра иногда выбирают в виде
1 3
1 2 3
( h h h )
.
Как уже отмечалось в разделе 3.4, операция пространственного
фильтрования коммутирует с дифференцированием по времени.
Однако по пространству коммутация может быть обеспечена лишь
изотропией сеточного разбиения, либо специальным учетом
анизотропии. Как уже отмечалось выше в обсуждении свойств
операции фильтрования, при дифференцировании соотношения,
определяющего операцию фильтрования для пространственной
координаты
x
, получается дополнительный интеграл от величины
с фильтром, равным производной от исходного фильтра
x x G x
,t d
x x x
,
Последний член обращается в нуль только для однородных по
пространству фильтров. Таким образом, при применении фильтра на
неравномерных сетках появляется дополнительная погрешность от
анизотропного фильтрования, связанная с коммутацией операций

75
дифференцирования. Разница
j j
x x
между этими членами
является ошибкой коммутации.
Существуют две возможности для получения фильтрованных
уравнений Навье-Стокса на неоднородных сетках
1) применение операции фильтрования к NSЕ в декартовых
координатах и последующее преобразование отфильтрованных
уравнений для применения на криволинейных сетках;
2) запись NSЕ в обобщенных координатах и последующее
применение операции фильтрования.
Эти сценарии изучались в [61,188] (Moin и др.), [86] (Jordan),
также рассмотрены в [153, 74].
В работе [61] эффект преобразования фильтрованных уравнений
обсуждался для одномерного случая. Показано, что введение
преобразования координаты приводит к коммутирующим фильтрам с
ошибкой в производных порядка
2
O
. В [188] показано, что данный
метод можно распространить на произвольный порядок точности
специальным выбором ядра фильтра.
Фильтрование в обобщенных координатах также исследовал
Jordan в [86], который предложил проводить операцию фильтрования
после применения преобразования уравнений NS к обобщенным
координатам, и показал, что ошибка коммутации при таком подходе в
некоторых случаях исчезает в силу того, что ядро фильтра действует
в однородном пространстве
3.8 Уравнения FNS в обобщенной криволинейной системе
координат
Уравнения FNS без учета сжимаемости в обобщенной
криволинейной координатной системе
, 1,2,3
i
i с обратным
якобианом
J
могут быть представлены в виде:
0
k
k
U
,
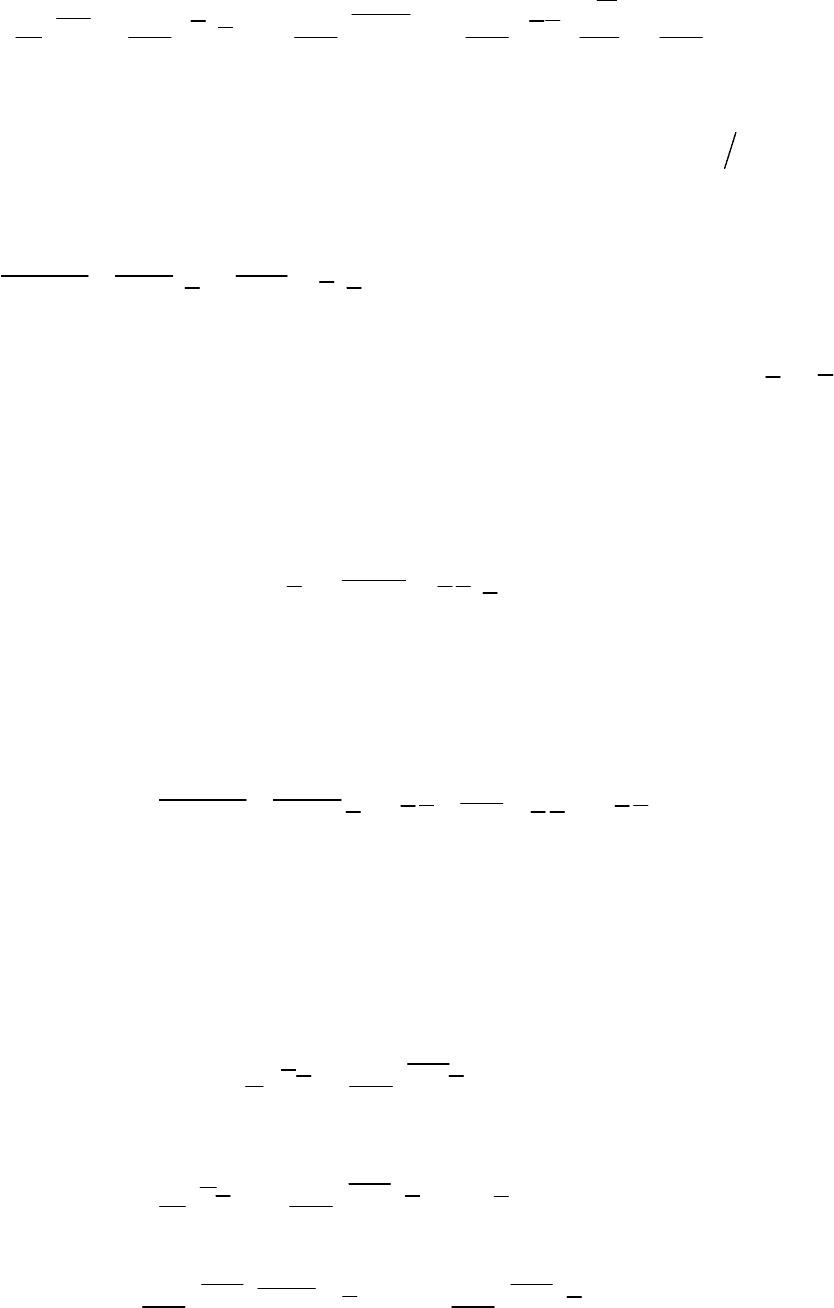
76
k k kl k
i
i i i i
k k k l k
u
Ju U u J p JG
t
.
Здесь коэффициент вязкости считается постоянным;
k k
i i
x
;
i
u
- декартовы компоненты скорости;
k k
i i
U J u
- контравариантные компоненты скорости;
k k k k k
i j i j j j i i
j
J u u J u u U u U u
- аналог подсеточного (SGS)
тензора, который является предметом дополнительной модели.
По замечанию [86] метрические величины, например
J
,
k
i
вычисляются в конечных разностях, поэтому могут считаться
фильтрованными на выбранной сетке. Поэтому приближенно
принимают
k k k
i i i i
U J u J u
.
Подсеточный тензор в криволинейной системе линейно связан с
подсеточным декартовым тензором
ij
k k k k k
i j i j j j j j i j i j j ij
J u u J u u J u u u u J
Уравнения FNS и уравнение энергии с учетом сжимаемости в
обобщенной криволинейной координатной системе
, 1,2,3
i
i при
тех же обозначениях принимают вид:
0
k
j j
k
J J u
,
k
i j i j ij ij
k
J u J u u p
t
k k
j i j i j j ij ij
k k
J u u u u J
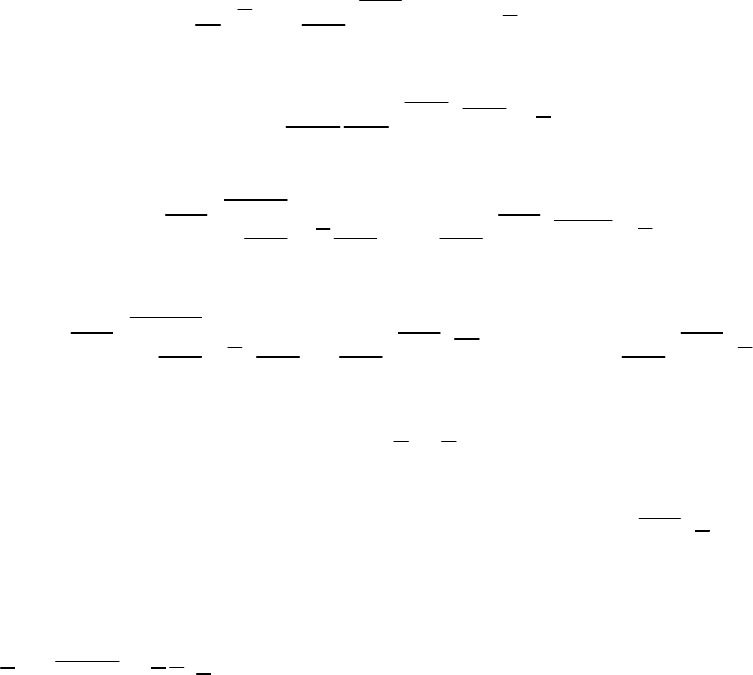
77
k
j j i ij j
k
ˆ ˆ
ˆ ˆ
JE J u E p u q
t
1
1
k
j j j
k
J pu pu
j j
k k
j i j i j i j
k k k
u u
J p p u J u u u u
j j
k k k
j ij ij j ij i ij j j j j
k k k k
u u
ˆ ˆ
J J u u J q q
R
p T
Здесь:
шапкой обозначаются синтетические величины;
k
j ij ij
J
- аналог
неразрешаемого тензора;
ˆ
E
- синтетическая полная энергия, которая
вычисляется; контравариантные компоненты записываются как
k k k
i i i i
U J u J u
аналогично несжимаемому случаю.
3.9 Представление нелинейного конвективного члена
Центральным вопросом при решении фильтрованных уравнений
Навье-Стокса является моделирование нелинейного конвективного
члена. Этой проблеме посвящены многочисленные попытки
представления нелинейного фильтрованного члена в виде разложения
через фильтрованные поля газодинамических переменных.
Разложение Леонарда (Leonard [105], 1974)
В работе [105] при применении фильтрующего оператора к
нелинейному конвективному члену уравнений Навье-Стокса
нелинейный член (в пренебрежении сжимаемостью) представлен в
виде функции
i
u
и флуктуации
i
u
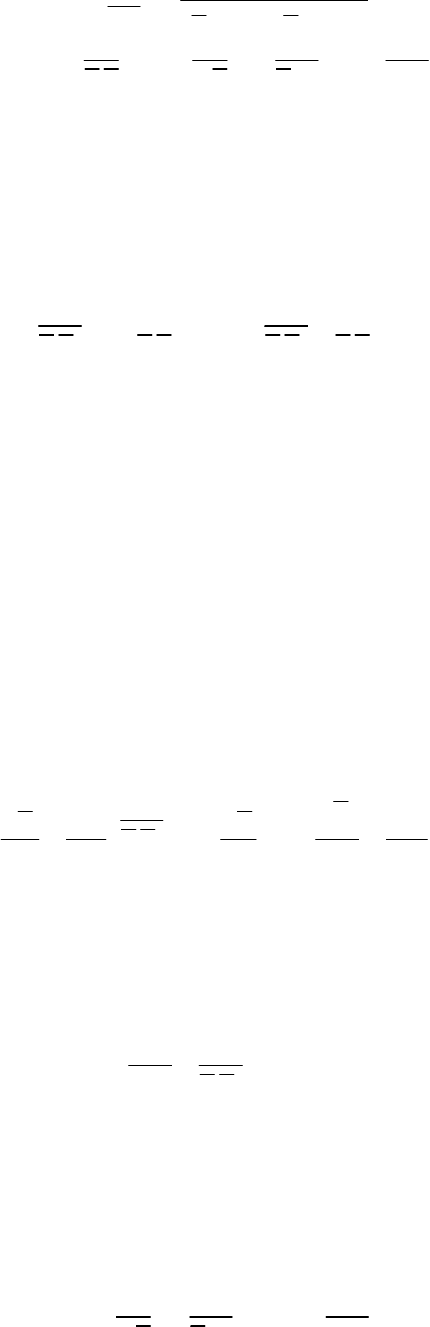
78
Рейнольдсовы
разрешаемые
перекрестные
напряжения
напряжения
напряжения
i i i j j
j
i i i j i j
j j
u u u u u u
u u u u u u u u
Это так называемое тройное разложение. В этом разложении
разрешаемый член может быть разложен далее
новый
тензорЛеонарда
разрешаемый
член
i j i j i j i j
u u u u u u u u
Такое представление называется разложением Леонарда.
Существует два способа представления уравнений импульса в
зависимости от выбора для формулировки разрешаемого
конвективного члена: 1) на основе тройного разложения; 2) на основе
разложения Леонарда.
В первом случае фильтрованное уравнение приобретает вид
уравнения движения
2
ij ij
i
i j
j i j j
S
u p
u u
t x x x x
Подсеточный тензор
ij
объединяет все неразрешаемые члены и
представляется в виде двойного разложения.
ij i j i j ij ij
u u u u C R
.
Здесь
C
- перекрестный тензор, описывающий взаимодействие между
большими и малыми масштабами;
R
- рейнольдсов подсеточный
тензор, описывающий взаимодействие между подсеточными
масштабами
;
ij i i j ij i j
j
C u u u u R u u
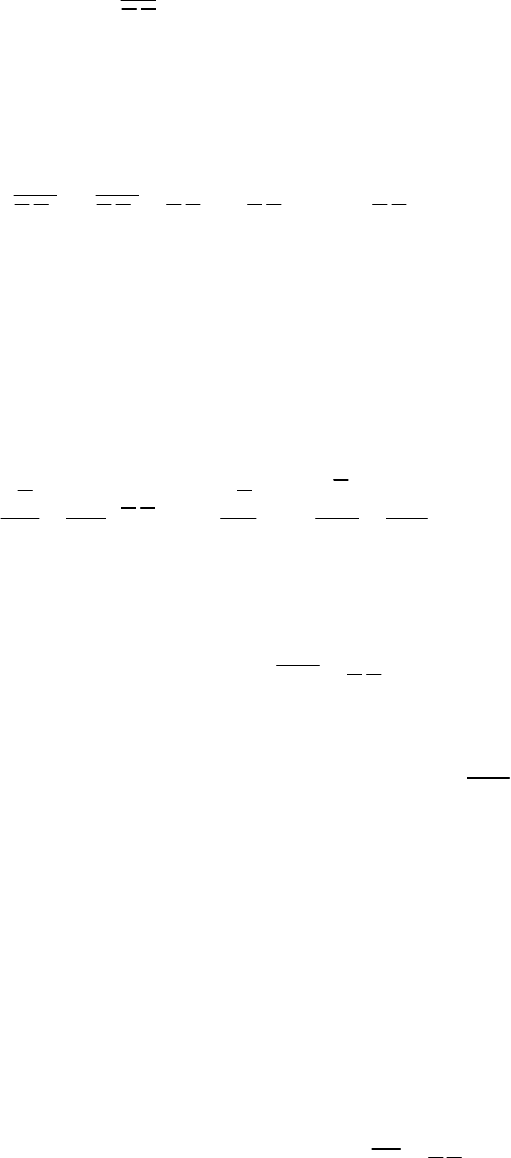
79
Другой способ заключается в том, чтобы члены в уравнении
импульсов могли быть оценены непосредственно по фильтрованным
величинам. Так как член
i
j
u u
не может быть представлен в виде
произведения фильтрованных значений полей, и требует повторного
фильтрования, то проводится дополнительное разложение [105]
тензор Леонарда
i j i j i j i j ij i j
u u u u u u u u L u u
Новый член – тензор Леонарда – отражает взаимодействие
разрешаемых масштабов при операции фильтрования. При
осреднении по Рейнольдсу такое взаимодействие не учитывается.
Фильтрованное уравнение NS приобретает вид
2
ij ij
i
i j
j i j j
S
u p
u u
t x x x x
здесь
ij
представляется в виде тройного разложения
ij ij ij ij i j i j
L C R u u u u
Если оператор фильтра является рейнольдсовым осреднением,
то тензоры
ij
L
и
ij
C
обращаются в нуль, тензор
ij i j
R u u
становится
рейнольдсовым корреляционным моментом (осредненным в смысле
Рейнольдса).
Представление Germano
Иное представление нелинейного члена предложено позднее в
работах (Germano, [51-58]). Формально Germano вводит обобщенный
момент двух величин
u
и
v
при фильтровании с ядром
G
,
G
u v G u v G u G v u v u v
Здесь выражение
G
обозначает операцию фильтрования случайной
величины
с помощью ядра
G
.

80
Аналоги трех составляющих корреляционных тензоров по
Леонарду теперь принимают вид
, , , , , ,
G G G
G G G G
L u u C u u u u R u u
В итоге тройное разложение представляется в виде
G G G
L C R L C R
.
На основе работ Germano развита теория сопоставления
фильтрованных величин, которая в дальнейшем была использована
при создании динамических моделей подсеточных напряжений.
Подсеточные тензоры, соответствующие двум различным
фильтрующим уровням отсечения с ядрами
F
и
G
, будем далее
условно обозначать:
G i j
u ,u
- крупномасштабный фильтр и
F i j
u ,u
- мелкомасштабный фильтр. На основании свойств
оператора фильтрования из свойства коммутативности можно
записать
i i i
FG F G
G
F
u u u
Тогда SGS тензор уровня
FG
представится в виде
FG i j i j i j
FG
FG FG
u ,u u u u u
Из свойств операции фильтрования и данного равенства следует
основное тождество Germano
FG i j F i j G i j
F
F
G
u ,u u u u , u
.
Тождество является локальным в пространстве и времени, и не
зависит от свойств фильтра. Из тождества следует, что SGS тензор
уровня
FG
состоит из вкладов SGS тензора уровня
F
,
отфильтрованного на уровне
G
, и SGS тензора уровня
G
,
рассчитываемого по полям, разрешаемым на уровне
F
.
