Солодов В.Г. Моделирование турбулентных течений. Расчет больших вихрей

Подождите немного. Документ загружается.

101

j i

x x

 



 

 

 

 

ij ij

ˆ ˆ ˆ

S S S



Подстановка в тождество Germano дает



ij kk ij ij

L L C C

   

  

где

ij ij

ˆ ˆ

S S

  

ij ij

S S

  

C C



Так как коэффициент

появляется внутри тестовой

фильтрующей операции, не представляется возможности

использовать это уравнение непосредственно для его определения.

Для продолжения моделирования Germano [59], Moin и др.[130]

пренебрегли тем, что

является функцией положения, и вынесли

за пределы операции пробного фильтра, тем самым предполагая

постоянство

в пределах размера фильтра. Такая аппроксимация

дает







ij kk ij ij

L L C

     

(i)

В результате для коэффициента

получается алгебраическое

соотношение вида

ij ij

L S

M S

  (ii)

где

ij ij kk ij

L L L

  

- анизотропная часть разрешаемых напряжений, а

тензор

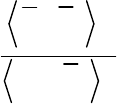
представляет собой разность



ij ij

   

102

Таким образом, величина

, полученная из алгебраического

соотношения (ii), становится знакопеременной.

Ghosal и др. [62] предположили, что отрицательные значения

могут означать локально отрицательную вихревую вязкость, которая

может свидетельствовать о потоке энергии от малых масштабов к

разрешаемым масштабам. Такой поток энергии действительно

известен, как обратное рассеяние энергии по каскаду, однако,

обоснование этой точки зрения имеет критиков в LES сообществе.

Подходящим настраиваемым параметром в модели является

отношение размеров масштабов

 

. По Germano [59] из априорного

теста следует, что оптимальная величина настраиваемого отношения

–

/ 2

 



. Однако в [59] указывается, что актуальное LES на основе

динамической модели показывает более интенсивную турбулентность

при этом значении отношения.

Использование полученного алгебраического выражения (ii) для

в LES в ряде случаев приводит к неустойчивостям счета. В тестах

для турбулентного каналового течения на основании данных из DNS

было найдено, что знаменатель соотношения для

может исчезать

или становится чрезвычайно малым, что ведет к вычислительно

неустойчивой величине

. Для преодоления этой проблемы величина

аппроксимировалась только как функция расстояния

по нормали

к стенке, и времени.

Чтобы сделать выражение (ii) для

совместимым с этим

предположением, было предложено осреднить числитель и

знаменатель через это однородное направление

ij ij

L S

M S

 

При этом, однако, такая процедура теряет часть концептуальных

преимуществ этой формулировки.

Lilly [109] отмечает, что уравнение (i) представляет собой пять

независимых уравнений с единственным неизвестным, поэтому нет

возможности удовлетворить эти уравнения одновременно. Поэтому

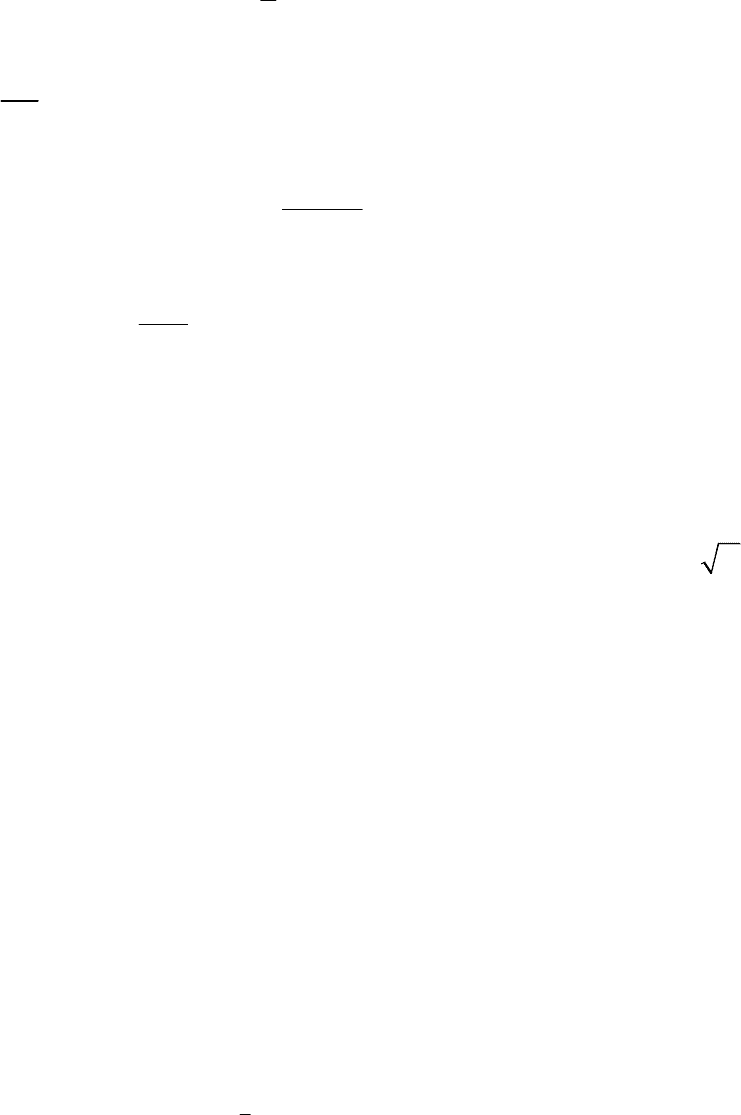
103

Lilly в [109] предложил модификацию модели Germano. Именно,

вместо конструирования

совместно с тензором

, предложено

минимизировать погрешность на основе метода наименьших

квадратов. В соответствии с этой модификацией можно получить

квадрат ошибки в виде

ij kk ij ij

Q L L CM

 

   

 

 

Из условия







величина

может быть вычислена как

ij ij

L M

  (iii)

Показано, что







, так что величина

представляет

локальный минимум

. Знаменатель отношения (iii) может

исчезнуть, только если каждая из пяти компонент

исчезнет в

отдельности, т.е. если напряжение тестового масштаба исчезнет

полностью. Но в этом случае исчезает и числитель.

Средняя величина динамического параметра

C C



полученного из соотношения (iii) оценивалась [175] вдоль

осесимметричной камеры сгорания при наличии вдува.

Распределение динамического

на горизонтальной средней

плоскости камеры сгорания показывает, что

выше в области более

высокой интенсивности турбулентности, т.е. ближе к входу.

Величина

затем уменьшается ниже по течению и исчезает на

выходе.

Численные эксперименты (например, [120]) показали

противоречивость алгоритма Germano–Lilly, который не приводит к

значению константы



при измельчении размера тестового

фильтра до значения, равного колмогоровскому масштабу длины, т.е

lim C





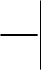
104

Трехуровневое фильтрование на основе тестовых фильтров

двух уровней

  



является развитием алгоритма Germano–

Lilly[142]. Данный подход приводит к необходимости введения

дополнительных гипотез и, в конечном счете, к степенному закону

масштабирования динамического коэффициента

. В конечном счете,

при рассмотрении двухуровневой процедуры тестового фильтрования

возникает проблема автомодельности фильтров, которая разрешается

лишь при специальном виде автомодельных фильтров [25].

Локализованная динамическая процедура определения

динамического коэффициента

для неоднородных течений

предложена в работе [62]. Процедура не использует линеаризацию

динамического коэффициента при применении тестового фильтра, а

основывается на минимизации девиатора тензора Леонарда.

Процедура сводится к решению интегрального уравнения Фредгольма

2-го рода при ограничениях на положительную определенность для

. Этот прием устраняет математическую несовместность алгоритма

Germano–Lilly, однако является чрезвычайно затратным [153].

Приближенная локализованная динамическая процедура

предложена Piomelli и Liu [138], основана на экстраполяции

девиатора тензора Леонарда



d *

ij ij ij

L C C

   

во времени. Коэффициент

выступает как оценка для

динамического коэффициента

. Авторы предлагают вычислять

оценку в виде временного полинома

* n

C C t ...





   



Здесь верхний индекс означает состояние коэффициента на







временном шаге. На практике авторы рассматривают экстраполяцию

второго порядка. Процедура, однако, не лишена проблем, связанных с

устойчивостью счета.

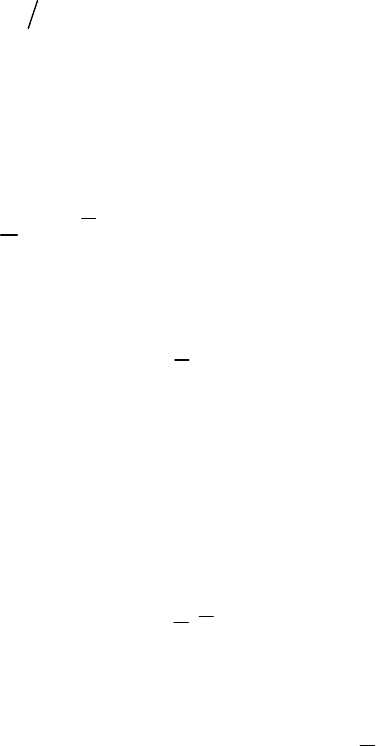
105

Sagaut и др. в [182] рассматривают обобщенную динамическую

процедуру, основанную на применении обобщенного тождества

Germano, которая дает теоретически более точные результаты в

сравнении с алгоритмом Germano–Lilly.

Многоуровневая процедура Terracol-Sagaut [182] разработана

как один из алгоритмов для динамического коэффициента

без

применения тождества Germano. Идея заключается в аппроксимации

спектра кинетической энергии степенным законом от волнового

числа





E k E k





Однако, как замечает Sagaut [153], параметры

E ,



могут зависеть от

числа Рейнольдса. Более точное представление для энергетического

спектра учитывает закон

5 3

Колмогорова.

Метод многих масштабов, основанный на уравнении

Колмогорова,

   

LLL LLL

r D r G r

   

развит Shao [160] на основе продольной корреляции 3-го порядка

фильтрованного поля скоростей





LLL

D r

и корреляции третьего

порядка скоростей-напряжений





LLL

G r

(гл.1). Подход базируется на

гипотезах автомодельности Колмогорова и использует аналог

многоуровневой процедуры Terracol-Sagaut [182] для подфильтрового

тензора





ij ij

C f u ,

  

Динамический коэффициент

получается при использовании

осредненной подфильтровой диссипации

ij ij

  

из уравнения

Колмогорова

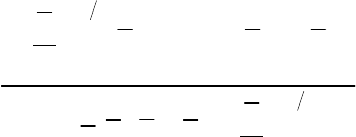
106

 

1 3

0 8

LLL LLL

ij ij

D r D

. f u , S r



 



 

 

 



 



 

  

 

 

Метод структурных сенсоров основан на информации о

структуре турбулентности, и направлен, прежде всего, на выявление и

оценку явления перемежаемости.

Метод развит в работе [36] (E.David) и основывается на оценке

угловых флуктуаций вектора завихренности. Основой для

установления критериальных связей явились результаты DNS анализа

развитого турбулентного течения. Установлено, что функция

плотности вероятности для локальной угловой флуктуации вектора

завихренности имеет всплеск вблизи 20

. Идея использования этого

факта заключается в проверке существования развитого

турбулентного течения, и основана на предположении, что

наивысшие разрешаемые частоты проявляют именно те свойства,

которые ожидаются в случае однородной и изотропной

турбулентности.

Метод частотной коррекции состоит в искусственном

увеличении вклада наивысших разрешаемых частот при оценке

подсеточной вязкости [153]. Такой прием возникает при применении

высокочастотного фильтра и позволяет лучше проявить явление

перемежаемости.

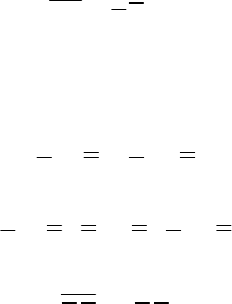
107

4.5 Математические модели подфильтровых напряжений,

основанные на подобии масштабов

Модели, использующие подобие масштабов, основаны на

гипотезе о том, что передача энергии через границу между

неразрешаемыми и разрешаемыми масштабами подобна передаче

энергии внутри разрешаемых масштабов вблизи границы. Отсюда

следует гипотеза о том, что неразрешаемые величины могут быть

вычислены на основе экстраполяции из пограничных разрешаемых

величин.

Модели, основанные на подобии масштабов, принадлежат к

категории структурного моделирования.

Несмотря на перспективу уточнения моделей низкого уровня

таким образом, модели, использующие подобие масштабов, как

показывает опыт, оказываются сложными в реализации и весьма

неустойчивыми в практике вычислений.

Модель подобия масштабов (Bardina и др. [9]) исторически

явилась первой моделью этого класса. В основе лежит двойная

операция фильтрования тройного разложения подсеточного тензора

на рейнольдсов, леонардов и перекрестный члены. При этом

повторное фильтрование предполагает приближенное фильтрование

произведения

  

В итоге члены тройного разложения представляются в виде









i i j j

R u u u u

  









i i j i j j

C u u u u u u

   

i i j

L u u u u

 

Окончательно, получается соотношение для модели Бардины для

подфильтровых напряжений

108





i j i j i j i i j

u u u u u u u u u u

    

Таким образом, модель оценивает действие неразрешимых

масштабов простой экстраполяцией с пограничных разрешаемых

масштабов. Оценка модели с помощью прямого численного

моделирования турбулентности (DNS) показала удовлетворительное

соответствие результатов, анализ [18] указывает на второй порядок

погрешности модели по размеру фильтра -

( )



. Отсюда следует

относительная погрешность модели порядка

(1)

Из частных случаев оценки передачи кинетической энергии

моделью, сделанных в [18], модель оказывается в ряде случаев

неустойчивой, за исключением

1 2







, что является весьма

жестким условием на величину фильтра.

Так как фильтр имеет 2-й порядок точности по величине

радиуса фильтра, то данная модель по порядку точности эквивалентна

градиентной модели (Leonard, [105]).

Динамическая модель Germano [59] по сути, использует

применение подхода Бардины к динамическому моделированию

коэффициента

в модели Смагоринского так, чтобы

подфильтровый тензор напряжений модели Смагоринского был

близок к аналогу модели Bardina в смысле наименьших квадратов.

Фильтрованная модель Bardina [76]. В данном варианте

модели подобия масштабов тензор подфильтровых напряжений

вычисляется как отфильтрованная величина SFS тензора модели

подобия масштабов Bardina. Результаты тестирования представлены в

[10]. Оценка энергетического баланса этой модификации модели

остается до настоящего времени открытой, в частности эффект

внедрения внешнего фильтра.

Еще одно обобщение модели Bardina также основано на

применении двух фильтров, т.е. двух отсекающих масштабов (Liu,

[111]), аналогично тому, как это сделано в динамической модели

Germano [59]

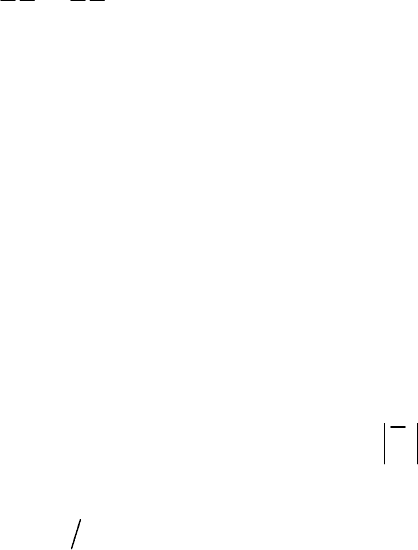
109











ˆ ˆ

i j i j i j

u u C u u u u

  

Здесь ячейка фильтра, обозначаемого шапочкой, является более

крупной. Константа пропорциональности

выбирается из условия

равенства точной и осредненной кинетической энергии. Там же Liu

предлагает динамическую версию модели, в которой коэффициент

вычисляется с помощью третьего фильтра.

Модель подобия на основе смешанных масштабов. В

смешанных моделях для улучшения устойчивости к тензору

подфильтровых напряжений добавляется член вида

 

C S



  ,

который аналогичен члену модели Смагоринского. Этот член

обеспечивает стабилизацию [10] при

1 2

 

и достаточно больших



- условиях, которые, однако, не выглядят перспективными.

Возможные направления развития моделей подобия

масштабов

Одно направление исследований связано с развитием модели

Bardina с целью достижения лучшей стабилизации. Как считает

Layton и др. [18], существует три идеи в развитии более точных и

устойчивых моделей:

-явная кососимметризация тензора подфильтровых напряжений

в версии Bardina. Подробности анализа изложены в [102, 101].

-модель низкого порядка точности, состоящая в пренебрежении

перекрестным и рейнольдсовым членами разложения;

- модели, основанные на экстраполяции высокого порядка

точности с разрешаемых масштабов на подфильтровые масштабы

типа Stolz-Adams [177-179], [155].

Модель экстраполяции высокого порядка Stolz-Adams.

Авторы развили семейство моделей [155], [177-179], хорошо себя

показавших на тестовых задачах.

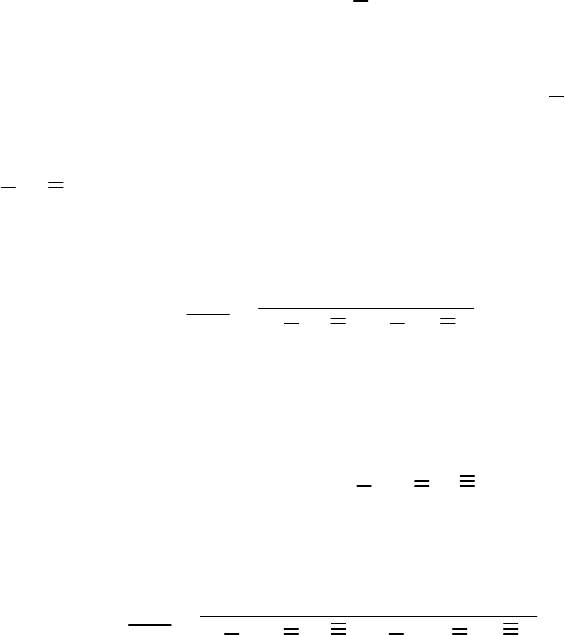
110

В моделях семейства экстраполяция с разрешаемых на

подфильтровые масштабы имеет 2-й порядок относительно размера

фильтра

( )

i i

u u O

 



Применение дифференциального фильтра





2 2



     

на

основе оператора Лапласа приводит к линейной аппроксимации

i i i

u u u





, что дает модель замыкания четвертого порядка по

величине фильтра [18]

 





2 2 ( )

i j i i j j

u u u u u u O

   

 .

Для квадратичной экстраполяции вида

3 3

     



соответствующая модель замыкания имеет вид









3 3 3 3 ( )

i j i i i j j j

u u u u u u u u O

     



На данном пути, используя экстраполяцию последовательно

нарастающего порядка, формально можно генерировать модели

любой асимптотически нарастающей точности. Однако вопрос

устойчивости таких моделей открыт.