Солодов В.Г. Моделирование турбулентных течений. Расчет больших вихрей
Подождите немного. Документ загружается.

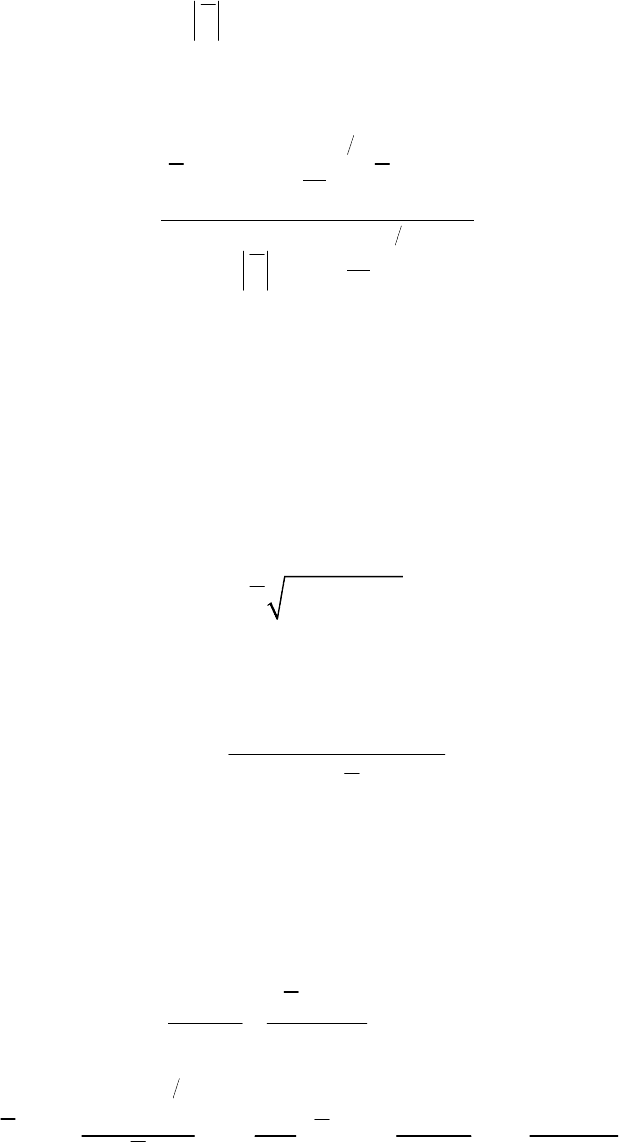
91
3) Двухпараметрическая (многомасштабная) модель, локализованная
в физическом пространстве.
Исходя из формулы
2
SGS
S
и используя два масштаба
1
r
и
2
r
, на
основании уравнения Колмогорова получается выражение для
подфильтровой вязкости вида
1 3
1
1 2
2
4 3
2
1
1
2
0 4 1
LLL LLL
SGS
r
D ( r ) D ( r )
r
r
. S r
r
Модель, основанная на подфильтровой кинетической
энергии, предложена рядом авторов [77,158,198,127,176,90]. В
модели подфильтровая вязкость вычисляется из кинетической
энергии подфильтровых пульсаций
SGS
K
:
2
SGS SGS
C K ( x,t )
Кинетическая энергия пульсаций представляется в виде
2
2
0 5
SGS i i
K . u ( x,t ) u ( x,t )
Кинетическая энергия
2
SGS
K
получается из решения уравнения
переноса (McComb [118])
2
2
j SGS
SGS
j
u K
K
t x
3 2
2
2 2 2
1 2
SGS
SGS SGS
ij ij SGS
j j j j
K
K K
S C C K
x x x x
Константы модели можно найти в [153, 118].
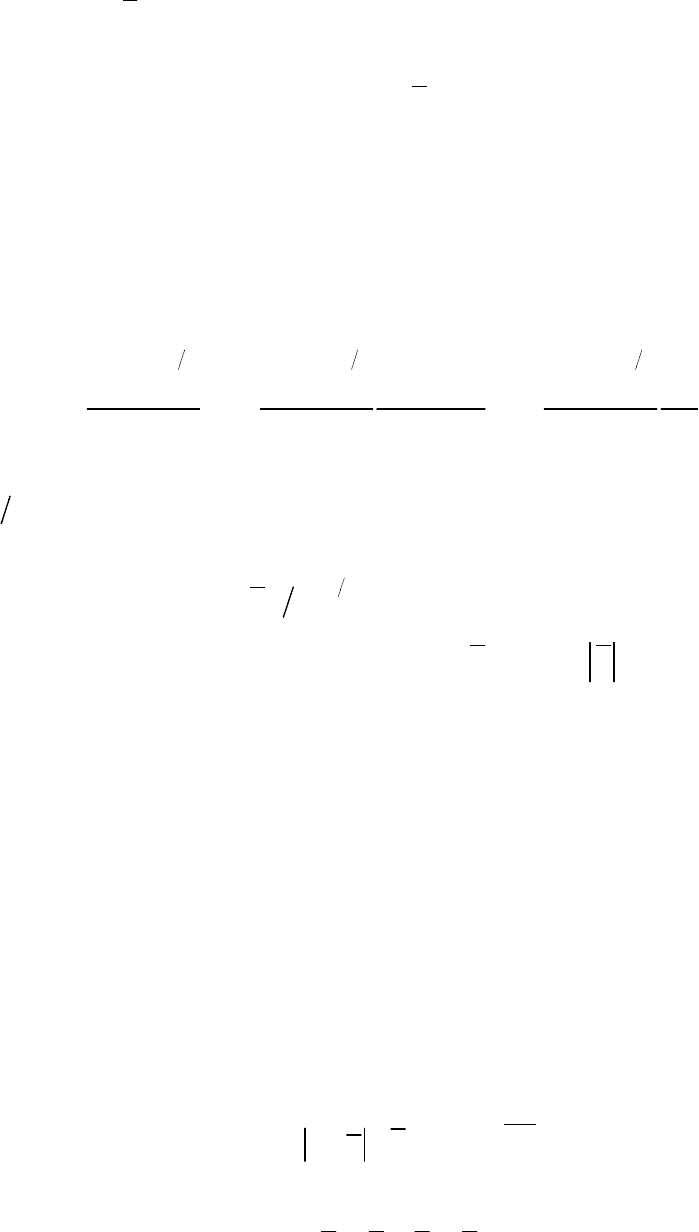
92
Модель Yoshizawa [199,197] для определения подфильтровой
вязкости использует характеристическую длину
f
, ассоциируемую с
подфильтровыми масштабами, и предполагает ее пропорциональной
длине отсечения
( , )
f S
C x t
Для улучшения разрешения Yoshizawa предлагает определять
f
из уравнения, связывающего диссипацию
и подфильтровую
кинетическую энергию
SGS
K [197]
3 2 3 2 5 2
2 2 2
2
1 2 3
2 3
SGS SGS SGS
SGS
f
K K K
D K
D
C C C
Dt Dt
Здесь
D Dt
- полная производная с конвективной составляющей по
разрешаемому полю скорости.
Используя оценку
1 3
1SGS
K C
, на основе гипотезы локального
равновесия Yoshizawa получает
3
2
5ij ij f
S C S
; константы
представлены в [197].
Как замечено в [153], характеристическая длина
f
может быть
интерпретирована как вариация константы Смагоринского.
Модель смешанных масштабов (Phuoc Loc и Sagaut [151,152]).
Однопараметрическое семейство моделей выводится на основе
взвешенного геометрического среднего моделей, основанных на
больших масштабах, и моделей, основанных на энергии масштаба
отсечения
1
1 2
2
SGS C
C rot u K
2
0 5
C i i i i
ˆ ˆ
K . u u u u
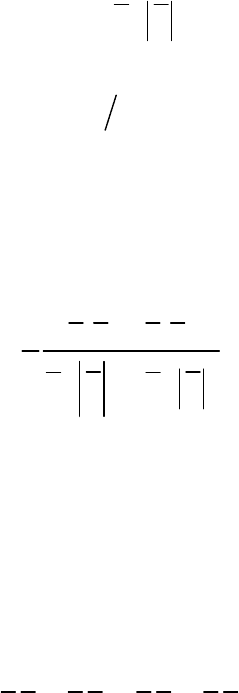
93
Здесь
2
C
K
- кинетическая энергия на масштабе отсечения при
использовании отсекающего тестового фильтра. Понятие тестового
фильтра изложено в разделе 4.4. Один из способов вычисления
2
C
K
основывается на гипотезе подобия Bardina (см. модель Bardina [9,10])
2 2
C SGS
K K
где
2
SGS
K
- кинетическая энергия подфильтровых масштабов.
Устойчивый диапазон значений
SGS
получается при
0 1
,
.
Анализ модели приведен в [18].
Подфильтровая кинетическая энергия на длине отсечения
может также оцениваться на основе модели Yoshizawa [199]
2
2 2
2
C I
K C S
где константа оценивается как
2
1
I
C
[46].
Коэффициент
I
C
, может быть оценен также с применением
тестового и основного фильтров по Germano [130] (тестовое
фильтрование обозначается шапкой; подробнее см. раздел 4.4).
2
2
2 2
1
2
k k k k
I
ˆ ˆ
u u u u
C
ˆ
ˆ
S S
При использовании формулы для
I
C
в таком виде возникает
численная неустойчивость, которая демпфируется с помощью
модификации Lilly и др. [194].
Другой способ оценки
C
K
основывается на тождестве Germano,
свертка которого дает
ii i i i i i i i i
ˆ ˆ ˆ ˆ
L u u u u u u u u
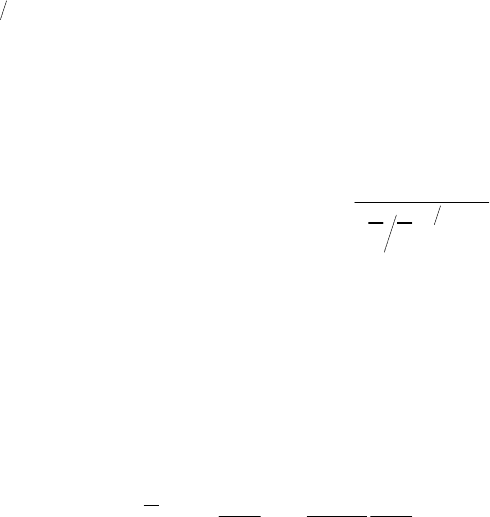
94
Если оба фильтра являются отсекающими по волновым числам
c
k
и
c
ˆ
k
, след тензора
ii
L
выражается через спектральную энергию
диапазона волновых чисел между отсечениями
2
c
c
k
ii
ˆ
k
L E k dk
Выражение для энергии следует из колмогоровского закона
5 3
E k C k
. В предположении попадания радиуса фильтра в
инерциальный поддиапазон можно получить выражение для
подфильтровой кинетической энергии
2
2 3
0 5
1
c
ii
C
k
L
K E k .
ˆ
При аппроксимации подфильтровых источников пассивной
скалярной величины
применяется градиентная модель [157]
(Schmidt, Schumann), основанная на представлении
0 7
SGS
SGS
i SGS SGS
j SGS j
J , .
x x
.
4.3 Некоторые направления усовершенствования моделей в
физическом пространстве
По экспериментальным данным целый ряд моделей ведет к
удовлетворительным результатам в основном в условиях
однородности и изотропии [153], а также при условии, что
фильтрование отсекает спектр далеко в инерциальной области, т.е.
большая часть спектра содержится в разрешаемых масштабах. В [222]
эта часть оценивается в 80-90%. Иногда в литературе упоминается
другой критерий, по которому отсекающий масштаб должен быть
порядка тейлоровского микромасштаба турбулентности.
95
Что касается случаев переходной турбулентности, а также
существенно анизотропных течений, то подсеточные модели, как
правило, показывают неудовлетворительные результаты.
По мнению P.Sagaut [153] основные характеристики таких
течений не соответствуют гипотезам, при которых были получены
модели. Существует ряд попыток описать свойства этих особых
случаев эмпирически. Другой путь ведет к повышению частоты
отсечения. Оба пути являются компромиссом между усложнением
подсеточных моделей и измельчением сетки.
Существует еще одна причина [153] неудовлетворительного
подфильтрового моделирования, которая обусловлена
существованием принципа неопределенности Габора-Гейзенберга. В
применении к разрешению турбулентных структур существует
принципиальная неопределенность в одновременном точном
определении частот в спектральном пространстве и положений в
физическом пространстве. Хорошее разрешение по частотам в
спектральном пространстве снижает степень локализации в
физическом пространстве, например в случае моделирования
перемежаемости и т.п. Наоборот, хорошее разрешение в физическом
пространстве приводит к ошибкам в вычислении спектральных
величин, в частности, энергии отсечения.
Проблема существует в связи с локализацией статистических
средних. Здесь могут быть рассмотрены два подхода к решению
проблемы [153]: а) уточнение приемлемого компромисса между
точностью в пространстве и частотой, и/или б) увеличение
информации, содержащейся в моделировании, что достигается
добавлением переменных, как в случае моделей, основанных на
кинетической энергии подсеточных мод, или выдвижением
дальнейших гипотез для развития моделей.
Ниже перечисляются приемы, развитые для улучшения
результатов моделирования без необходимости глубокой
модификации структуры подсеточных моделей. Цель таких
модификаций - адаптировать подсеточную модель к локальному
состоянию потока и исправить недостаточность частотной
локализации информации. В числе основных приемов, направленных
на достижение данной цели выделяют [153]:
96
1. Динамические процедуры для вычисления коэффициентов
неразрешаемых моделей. Процедуры направлены на снижение оценки
ошибки, совершенной с рассматриваемой моделью локально в
пространстве и времени в смысле наименьших квадратов. Такая
оценка делается с использованием тождества Germano и требует
использования аналитического фильтра. Основные свойства и
структура моделей, такие, например, как линейная связь тензоров
напряжений и скоростей деформаций, остаются неизменными.
2. Динамические процедуры, которые прямо не используют
тождество Germano. Сюда относятся многоуровневая процедура
(Terracol-Sagaut) и метод корреляционных моментов многих
масштабов (Shaо). Эти процедуры также используют определение
тестового уровня фильтра и основываются на рассмотрении
процедуры масштабирования диссипации как функции разрешения.
Процедуры также неявно используют предположение о частичной
автомодельности течения.
3. Структурные сенсоры, которые тестируют и подтверждают, что
наивысшие разрешаемые частоты проявляют именно те свойства,
которые ожидаются в случае однородной и изотропной
турбулентности
4. Метод частотной коррекции, который состоит в искусственном
увеличении вклада наивысших разрешаемых частот при оценке
подсеточной вязкости. Такой прием возникает при применении
высокочастотного фильтра и позволяет лучше проявить эффект
перемежаемости.
Таким образом, три методики - динамическая процедура,
применение структурного сенсора и метод частотной коррекции
основываются на извлечении тестового поля из разрешаемых
масштабов. Это поле соответствует наивысшим частотам,
выделенным моделированием. Поэтому эти методики основаны на
частотной локализации информации в подсеточных моделях.
97
4.4 Многоуровневое фильтрование
Дополнительная информация для оценки коэффициентов при
вихревой вязкости получается сравнением результатов
моделирования на фильтрах двух или нескольких разрешаемых
уровней: основном и тестовых (или пробных), величина которых
грубее основного.
Исторически такая динамическая процедура впервые была
предложена Germano в [103] для модели подсеточных напряжений
Смагоринского. В целом, Germano на основе тройного разложения
Леонарда (гл.2) развил мультипликативную процедуру фильтрования,
поддерживающую многоуровневое фильтрование, которое явилось
основой для построения многоуровневых моделей, в том числе и для
анизотропных течений.
Динамическая модель для коэффициента
S
C
[102]
Рассмотрим подробнее динамическую процедуру Germano для
случая основного и тестового размеров фильтра. Один из уровней
фильтрования считается вспомогательным или тестовым. В
соответствии с [102] рассмотрим функцию тестового фильтра
ˆ
для вычисления коэффициента Смагоринского
S
C
. Здесь и ниже
шапочка над символом обозначает операцию фильтрования тестовым
фильтром
ˆ
ˆ
x,t ,t G x , x d
В простом случае несжимаемой среды неизвестные члены в
уравнениях переноса импульса
i j
u u
определяются согласно Germano
[129] как
i j i j ij
u u u u
где
ij
неизвестный член, относящийся к неразрешаемым
напряжениям и скалярным источникам, который должен

98
моделироваться. Аналогичное представление
ij
T
записывается и для
тестового уровня фильтра.
Общий подход заключается в том, что тензоры
ij
и
ij
T
двух
различных уровней фильтрования должны моделироваться по
разрешаемым полям. На основании тождества Germano (гл.3) для
двух уровней можно записать
ˆ
ij ij ij
L T
Величины, входящие в тождество Germano, представляются
через фильтрованные величины следующим образом
ij ij ij ij i j i j
L C R u u u u
,
аналогично
ˆ
ˆ ˆ
ij ij ij ij i j i j
T L C R u u u u
,
откуда вытекает
ij i j i j
L u u u u
Тензор Леонарда
ij
L
, в отличие от тензоров
ij
и
ij
T
, может быть
вычислен непосредственно по разрешаемому полю параметров.
Для девиаторов подсеточных тензоров основного и тестового
уровней возможно следующее представление
1
3
ij kk ij d ij
T T C A
1
ˆ
3
ij kk ij d ij
C B
здесь
A
и
B
- девиаторы подсеточных тензоров. При этом
предполагается равенство коэффициентов пропорциональности,
которое эквивалентно одинаковой масштабируемости подсеточных
потоков.
В итоге для тензора Леонарда на основании тождества Germano
получаем
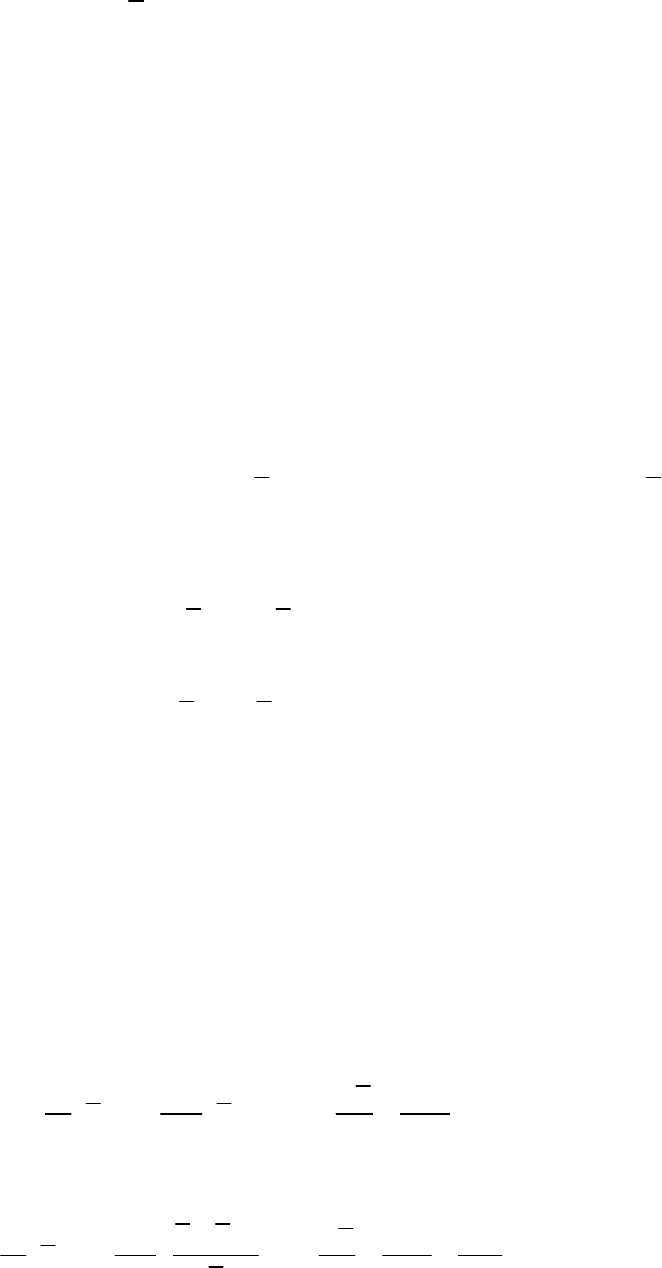
99
1
3
D
ij
ij kk ij ij d ij
L L L C A B
при условии
ij
d ij d
C B C B
,
которое эквивалентно условию постоянства
d
C
вблизи радиуса
фильтра. В результате центральным вопросом подсеточной модели
является определение коэффициента
d
C
, который уже не является
константой, а изменяется динамически.
Аналогичная процедура выполняется при фильтровании
уравнений движения сжимаемой среды. Пусть неизвестные члены в
уравнениях переноса импульса
i j
u u
и переноса скаляра
j
u
определяются согласно Germano [60] как
i j i j ij
u u u u
и
SGS
i i i
u u J
,
где
ij
и
SGS
i
J
неизвестные члены, относящиеся к подфильтровым
напряжениям и скалярным источникам, должны моделироваться.
Аналогичное представление выполняется и для тестового уровня
фильтра.
Фильтрованные по Фавру уравнения движения для сжимаемой
среды в этом случае имеют вид
ij
i i j
j i j
p
u u u
t x x x
,
Отсюда
ij
i j ij
i
j i j j
u u T
p
u
t x x x x
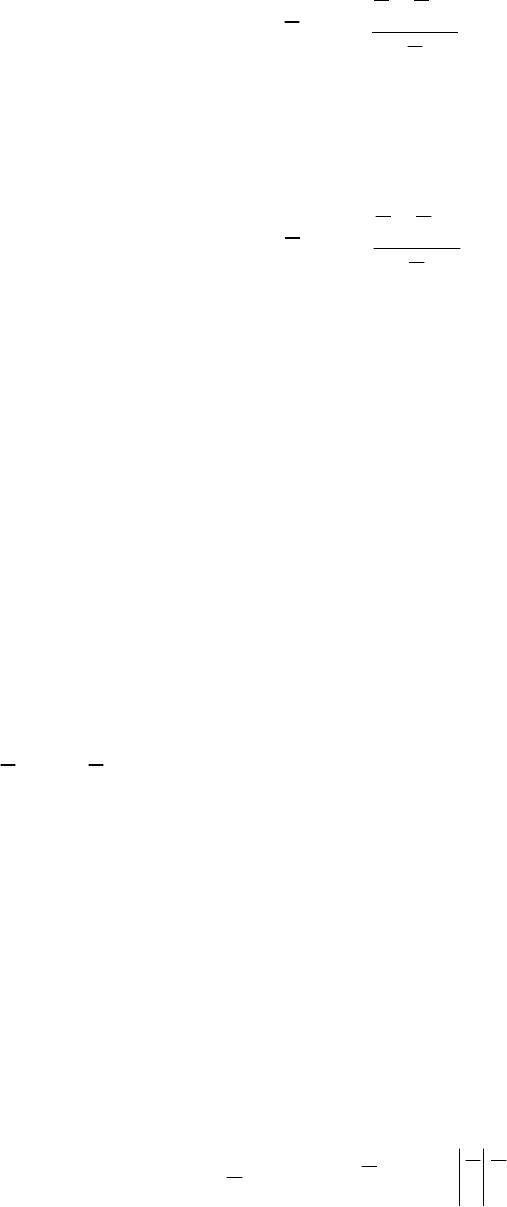
100
В этом случае тестовые подсеточные напряжения
ij
T
представляются
в виде
i j
ij i j
u u
T u u
С другой стороны, разрешаемые леонардовы турбулентные
напряжения определяются как
i j
ij i j
u u
L u u
и могут быть вычислены по крупным вихрям.
Разрешаемые турбулентные напряжения представляют собой
вклад в рейнольдсовы напряжения посредством масштабов, величина
которых является промежуточной между шириной сеточного
фильтра и шириной тестового фильтра, т.е. малых разрешаемых
масштабов. Следовательно, величины в этих соотношениях связаны
тождеством Germano
ij ij ij
ˆ
L T
,
где
ij i j i j
ˆ
u u u u
- применение тестового фильтра к подсеточным
напряжениям
ij
.
Тождество Germano используется для усовершенствования
модели SGS напряжений с помощью локального уточнения текущей
величины коэффициента Смагоринского. При использовании этого
тождества предполагается, что одна и та же функциональная форма
может быть использована для моделирования как
ij
T
, так и
ij
. Для
модели Смагоринского
2
1
ˆ ˆ
ˆ
ˆ
2 ( )
3
ij kk ij S ij
T T C S S
где
