Солодов В.Г. Моделирование турбулентных течений. Расчет больших вихрей

Подождите немного. Документ загружается.

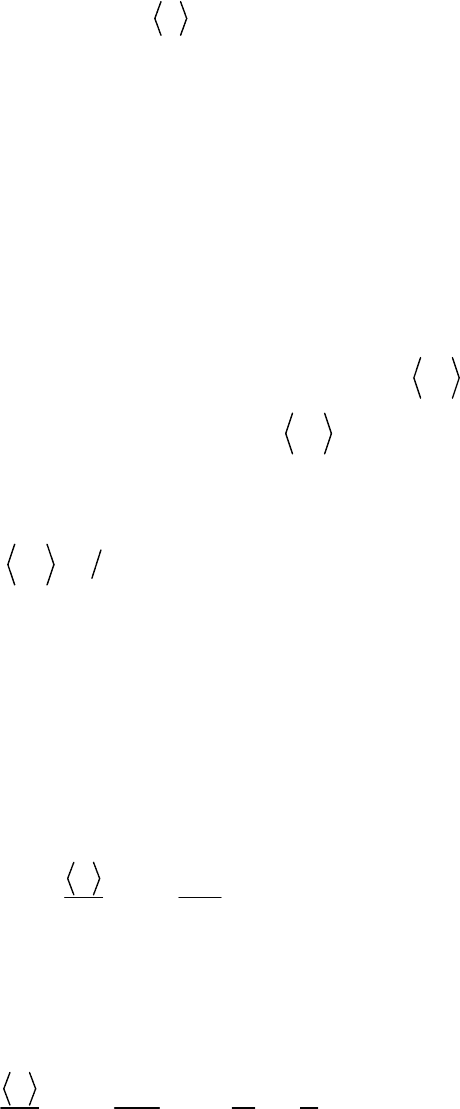
121

x x l







- переменная пограничного слоя;

l u

 

 

- характерная

вязкая длина; знаком «+» обозначаются величины, выражаемые в

пристенных единицах. Тогда характерные параметры пограничного

слоя

( ); / ; /

u f x u u u y u x

   

 

   

Различают четыре подслоя пограничного слоя (см.

например[153]):

внутренняя область, где доминируют эффекты молекулярной

вязкости

(0 0.2 )

  

;

внешняя область, где проявляет свои свойства турбулентность.

Во внутренней области, в которой процессы описываются в

переменных пограничного слоя, можно выделить слои:

а) вязкий (ламинарный) подслой:





, для которого

u x

 



;

б) буферный слой:

5 30



 

, для которого

5ln 3.05

u x

 





;

в) инерционный логарифмический слой:

30 , / 1

x x









, для которого

1 ln 5.5, 0.4

u x

 

 



 

Внешняя область включает границу логарифмической

инерциальной области и область турбулентного следа, описывается

во внешних переменных.

Осредненный профиль скорости для логарифмической

инерциальной области описывается в виде:

A B









где

A B

- константы.

Для области турбулентного следа:

C x

A B W



 

 

 

  

 



где

, ,

A B C

- константы,

- функция Клаузера.

122

Наблюдения и DNS анализ [153,67,139,110,87] показывают, что

среда в глубине пограничного слоя состоит из перемежающихся

областей быстрого и медленного движения, организованных в

полоски, прожилки или стрики, которые в переменных стенки имеют

постоянные размеры. Низкоскоростные области мигрируют к

внешней стороне внутреннего пограничного слоя, где вследствие

неустойчивости разрушаются взрывоподобно. Эти взрывы

сопровождаются опусканием быстрых объемов среды к стенке,

организуя полосчатую структуру. Такие интенсивные события

индуцируют вариацию рейнольдсовых напряжений и производят

значительную долю флуктуаций переменного знака в диапазоне

подсеточной диссипации.

DNS анализ демонстрирует интенсивную мелкомасштабную

диссипацию в буферной области. Максимум производства

турбулентной энергии наблюдается при





, что приводит к росту

интенсивности обратного энергетического каскада (обратного

рассеяния энергии). Во внешней области пограничного слоя

доминирует прямое рассеяние турбулентной энергии.

Как отмечается в [153], DNS результаты показывают, что

пристенная турбулентность ниже значения





в значительной

степени автономна и ответственна за производство большей части

турбулентной кинетической энергии, диссипируемой во внешней

части пограничного слоя.

Структура и механизм турбулентности, прямое и обратное

рассеяние энергии в пограничном слое определяют специфические

подходы к разрешению турбулентности. Cледует отметить, что в

приграничных областях нарушается свойство изотропности

турбулентности.

Прямое разрешение пристенной динамики требует достаточно

высокого сеточного разрешения при применении условия стенки без

проскальзывания. На практике это вынуждает выполнять размещение

первой расчетной точки в зоне

0 1



 

. Для представления

генерирующих механизмов Schumann [159] рекомендует

пространственное разрешение со сгущением

1 2 3

10, 5, 2

  

     

123

Zang [202] понижает это разрешение до

1 2 3

80, 30, 10

  

     

Piomelli [137] использует

244



 

для плоского каналового течения.

Средняя оценка для схем 2-го порядка точности сводится к

величинам

1 2 3

100, 20, 2

  

     

. Bagget и др. [6] указывают, что

количество степеней свободы при моделировании погранслоя в

случае отображения динамики подслоя оценивается по порядку как







Для уменьшения числа степеней свободы и во избежание

вхождения во внутренний подслой используются модели для

представления динамики этой зоны – так называемые специальные

подсеточные модели стенки. В этом случае условие прилипания не

применяется, так как дистанция от стенки до первой точки больше

характерного масштаба мод, существующих в этом слое. Такой

подход позволяет помещать первую точку в логарифмическом слое

20 200



 

, хотя это привносит дополнительную ошибку.

5.2 Основные модели стенки

В связи с плохой обусловленностью задачи приближенного

моделирования граничных условий вблизи стенки для реальных

размеров фильтра, и особенно для фильтров постоянного радиуса,

существует обширная литература по пристенным моделям

турбулентности, основанная на различных «законах стенки».

Историю вопроса и набор полуэмпирических моделей можно

встретить в [192, 141].

Как правило, это логарифмический закон в пограничном слое, с

различными эмпирическими константами. Если за основу принять,

например,

 

модель турбулентности, разрешающую параметры

вдали от стенки, то требуется моделировать часть пограничного слоя



, который не описывается моделью. При этом переходят к

переменным пограничного слоя [223] и аппроксимируют вязкий

подслой (толщиной около

0 2



) по линейному закону, а ядро

пограничного слоя - по логарифмическому закону, например по

законам Прандтля-Тейлора или Рейхардта [223].

124

Вместе с тем, для LES существует ряд отличий в моделях в

сравнении с URANS. Прежде всего, LES описывает существенно

нестационарные явления во всей области течения, которые не могут

опираться на равновесный пристенный профиль.

В связи постоянством размера ячейки фильтра в достаточном

тонком и существенно важном с точки зрения генерации вихрей

вязком подслое происходит осреднение по большим масштабам.

Дополнительной проблемой пристенного моделирования является

нелокальность, возникающая, в основном, вследствие ошибки

коммутации.

Обширный обзор пристенных моделей в LES опубликован в

[153, 135].

Одна из естественных и популярных трактовок реализации

граничных условий в LES - это переход к очень малым значениям

размера фильтра



при приближении к границе. Сюда же следует

отнести реализацию граничных условий на стенке, обеспечивающую

прилипание



. Как уже отмечалось (гл. 3), эти условия влекут за

собой ошибку коммутации фильтрования и производной вблизи

границы





Er u

даже для гладкой функции

. Оценка погрешности

выполнена в работах [18,45, 61, 188].

Следует отметить некоторые трудности на пути решения

проблемы. В частности, теоретический подход к проблеме,

основанный на одномерном анализе при разложении в ряды для очень

гладких функций [188], вообще говоря, плохо соответствует

проблеме. Необходимость уменьшения радиуса фильтра в

направлении стенки связана с измельчением сетки во внутреннем

подслое. При этом оценки, выполненные в работе [135], показывают,

что затраты на прямой расчет турбулентных каналовых течений

значительны. Так, в вязком подслое затраты пропорциональны





2 4

O Re

, а во внешнем слое -

( )

O Re

. В практически важных

течениях, где числа Рейнольдса достаточно велики, точный LES

расчет приложений с выявлением отрывных явлений на гладких

стенках становится нереализуемым. Поэтому дальнейшая разработка

пристенных моделей является актуальной.

125

5.3 Применение фильтров переменного радиуса

Фильтры переменного радиуса возникают, как правило, вблизи

границ области. Границы порождают анизотропию, усложняют

построение моделей турбулентности и, как отмечалось в гл.3, создают

проблему коммутации. Следует заметить, что анизотропия

появляется, прежде всего, при описании пограничных слоев и может

быть устранена только при асимптотическом удалении от стенок.

Для простейшего случая коробчатого фильтра операция

фильтрования может быть определена как

   

 





( )

y y

y d

y y









 

    

  



 ,

где

















значения эффективной ширины фильтра,

локализованные в положении

. Погрешность







процедуры

фильтрования вследствие коммутации при переменной длине фильтра

приобретает вид

 

   









d y y

y y dy

 

   

 

   

  

 





 





   

d y d y

y y y y

dy dy

y y

 

 

   

   

      



  

Ошибка коммутации







между фильтрованием и

дифференцированием приводит к тому, что каждый

пространственный оператор в уравнениях генерирует члены, которые

не могут быть выражены исключительно в терминах фильтрованных

полей. Поэтому проблема замыкания лежит не только в наличии

квазилинейных членов конвективного оператора, но и в линейных

членах при условии анизотропии сетки, ассоциируемой с

анизотропным фильтром. Например, Das и Moser [35] показали, что в

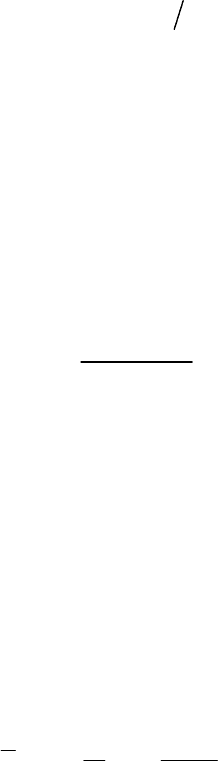
126

большинстве LES приложений на неоднородных сетках не

удовлетворяется уравнение неразрывности, даже для модели

несжимаемой среды.

Moin в [61] (см. также [128]) предложил альтернативное

определение фильтрующего оператора путем введения отображения,

трансформирующего расчетную область с анизотропной и

неравномерной шириной фильтра в систему координат, где ширина

фильтра постоянна.

Такое отображение представляется в виде гладкой монотонной

функции





f x

, отображающей интервал





a,b

на



. В этом случае





lim

x a

f x



 

, и





x b

lim f x

 

→

В результате получается, что









x f x



  

Отсюда вытекает, что





f x



на концах интервала должна быть

бесконечной, то есть ядро фильтра является дельта-функцией Дирака

на границах интервала.

Наиболее часто, например для «каналовых» течений, выбирают

следующий вид





f x

 

x a b

f x th

b a



 

 



 



 

при

a x b

 

Для произвольной скалярной функции





u x

при замене переменных

 

получается новая функция

















1 1

u f , x f ,

 

      



Окончательно получается следующее отображение

   

g d

  

 

     

 

 

 





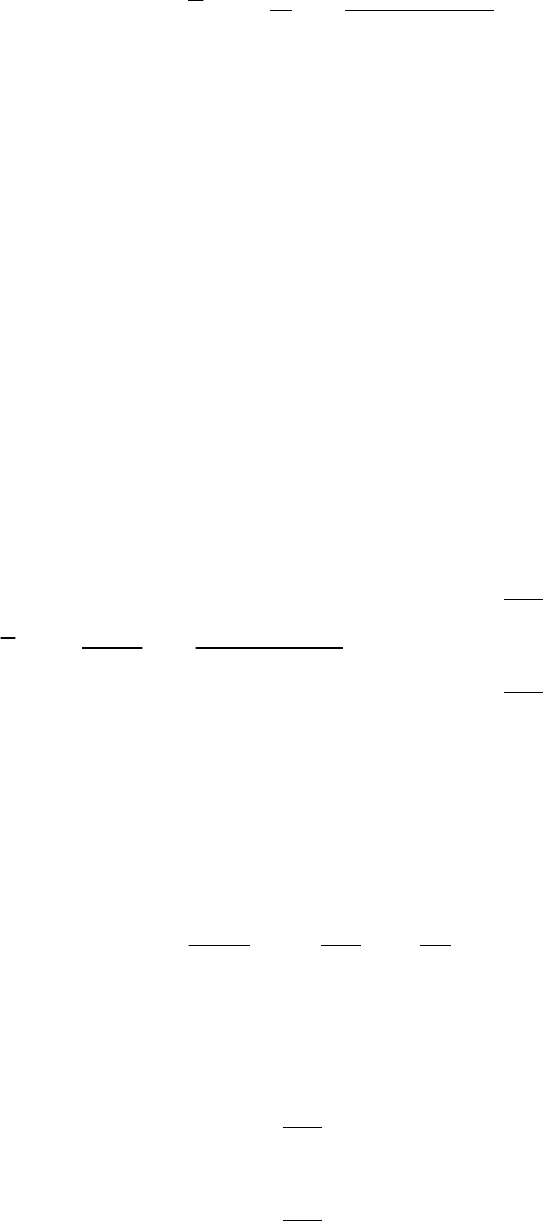
127

При обратном отображении получаем

 









   

f x f y

u x g u y df y

 



 

 

 



Как показано в [18,61] путем разложения в ряд Тейлора, ошибка

коммутации даже для гладких





u x

значительна, и удовлетворяет

условию









Er u O

 

Распространение одномерного отображения на трехмерный

случай выполняется непосредственно,





f y



заменяется якобианом

преобразования.

В работах [188, 116], (см. также [18]) намечены пути

уменьшения ошибки на примере общей операции фильтрования

 

   

 

     

 

, ,

x a

x b

f x f y

u x g x u y dy g x u x x d

x x









 



      

 

 

 

 

 

 

Здесь





g x,y

функция фильтра, зависящая от положения.

Величина ошибки представляется в виде ряда Тейлора

 

         

 

i i i N

i N

d d

Er u x u x x M x O x

i dx







 

    

 



с весовыми множителями – моментами функции фильтра [116]

   

 

, , 0,..., 1

x a

i i

x b

M x g x d i N









     



128

Однако, как указывает [18], такое разложение сходится в случае

однородного фильтра



, в предположении, что спектр





u x

не

включает волновые числа выше некоторого конечного волнового

числа отсечения. Следует также заметить, что оценка выполнена при

очень сильном предположении о дифференцируемости и

ограниченности





u x

Ошибку коммутации также изучал Germano [51,49], который

ввел в практику исследования LES линейные дифференциальные

фильтры. Для них ошибку коммутации удается выразить через

разрешаемые масштабы [50] подобно леонардовым напряжениям.

5.4 Случай фильтров постоянного радиуса

Фильтры постоянного радиуса в случае реализации

приобретают перспективу в связи с исчезновением ошибки

коммутации, и возможностью существенного снижения

вычислительных затрат в области пограничного слоя. Вместе с тем

осреднение с применением конечного фильтра постоянного радиуса

вблизи границы является существенно нелокальным, и поэтому

вступает в противоречие с обусловленностью задачи [18].

Вопрос первоначально прорабатывался в работах [35,41,82],

сейчас имеет обширную литературу, характеризуется пока еще

значительной математической сложностью.

В работе [35] Das и Moser применяют достаточно неожиданный

подход – присоединение к вычислительной области с внешней

стороны стенки буферную внешнюю область с нулевой скоростью.

Напряжения на стенках вычисляются из решения задачи

минимизации кинетической энергии с включением буферной области.

В работе показана хорошая обусловленность задачи и намечен

алгоритм градиентного поиска.

Таким образом, вопрос об ошибке коммутации на неоднородных

сетках и в приграничных областях требует еще дополнительных

исследований.

Следует, однако, заметить, что поскольку в LES сеточный

размер приближенно по порядку равен ширине фильтра, и если для

129

представления производных используются численные схемы 2-го

порядка точности, то на неоднородных фильтрах возникает конечно-

разностная ошибка того же порядка, что и ошибка коммутации

пространственного дифференцирования и фильтрующего

оператора[128].

Таким образом, в LES для турбулентных течений на

неравномерных сетках с использованием разностных схем 2-го

порядка фильтрующая операция может приближенно предполагаться

коммутирующей с пространственным дифференцированием в рамках

точности численной аппроксимации. Поэтому во многих прикладных

исследованиях на этом основании ошибкой коммутации

пренебрегают.

130

6. ГИБРИДНЫЕ МАТЕМАТИЧЕСКИЕ МОДЕЛИ

RANS/LES

Ряд причин побуждает к поиску упрощенных подходов в

моделировании турбулентности, в частности, к гибридизация

RANS/LES.

Основная причина – это рост затрат на моделирование в рамках

традиционного LES подхода при необходимости учета всех основных

масштабов при производстве турбулентности. Также следует

отметить наблюдаемую неспособность большинства подсеточных

моделей корректно учитывать анизотропию и неравновесность

турбулентности. Последнее особенно актуально для процессов во

внутренней области пограничного слоя. Одним из возможных

решений является смешение LES с RANS подходом именно в

пограничном слое.

Существует несколько вариантов гибридизации, которые

примерно классифицируются следующим образом [90].

Зональное представление. Общая вычислительная область явно

или неявно (заранее или в процессе расчета) делится на домены, в

некоторых течение рассчитывается на основе RANS модели, в других

- на основе LES.

Метод возмущений. Идея заключается в вычислении поля

течения на основе URANS, что представляет низкочастотную часть

решения, и в последующем производится реконструкция

недостающей части флуктуирующего поля на основе LES подхода.

Это эквивалентно зональному мультидоменному подходу [73,71,72]

(Hoffman), в спектральном представлении [95].

Универсальное моделирование. При универсальном

моделировании модель SGS напряжений заменяется обобщенной

моделью – комбинацией RANS модели и подходящей SGS модели.

Такое слияние, как ожидается, в перспективе может внести больше

физического содержания в SGS модель, а SGS модель в свою очередь

должна эффективно представлять решение для низкочастотной части

спектра (в начале инерциального поддиапазона).