Солодов В.Г. Моделирование турбулентных течений. Расчет больших вихрей
Подождите немного. Документ загружается.

111
4.6 Класс моделей, основанных на асимптотике волновых
чисел.
Название данного класса моделей – approximate deconvolution
(AD) – интерпретируется как методология приближенного обращения
фильтра или «дефильтеринга» (Schlatter [156]), иначе, приближенно
восстанавливающая методология.
Кратко общая схема AD методологии заключается в следующем
([18]). На первом шаге ко всем членам замыкания применяется
преобразование Фурье. Затем производится асимптотическое
разложение для экстраполяции преобразованных членов в
пространстве волновых чисел в окрестности отсечения по фильтру.
На заключительном шаге к полученным приближенным
зависимостям применяется обратное преобразование Фурье для
получения аппроксимаций исходных членов замыкания в физическом
пространстве.
Известен ряд моделей данной методологии, которые в основном
развивают Adams, Berselli-Iliescu, Layton и ученики. Ниже
рассматриваются три представительные модели данного направления:
градиентная (GLES), восходящая к работам (Leonard [105], Clark и
др.[31]), рациональная модель (RLES) (Galdi, Layton[47]), и модель
подфильтрового масштаба повышенного порядка (HOSFS) (Berselli,
Iliescu[19]).
В отличие от моделей вихревой вязкости, в которых неявно
фигурируют различные виды фильтров, важной составляющей ADM
является применение исключительно гауссового фильтра, как
удобного при преобразовании Фурье.
Градиентная модель
Подробное изложение основных свойств моделей замыкания
или тензора
i j i j
u ,u u u u u S u ,u
, представлено в [18] Именно,
применение операции свертки при использовании гауссового фильтра

112
в виде
2
3 2
2 2
/
x
G x, exp
к случайной величине
i i i
u u u
, где
i i
u G* u
, ведет к преобразованию Фурье,
i i i
u k G k * u k G k * u k
,
где
1 2 3
k k ,k ,k
- волновой вектор. Отсюда получается связь между
флуктуацией и средним в спектральном пространстве
1
1
i i
u k u k
G k
.
При оценке членов SFS тензора
i j i j
u ,u u u u u
в градиентной
модели для ядра
G k
используется разложение в ряд Тейлора по
волновым числам с точностью до членов 4-го порядка по радиусу
фильтра
:
2
2
4 4
1
4
G k k O k
,
2
1
2
4 4
1
4
G k k O k
.
Здесь ключевой момент методики. После подстановки в SFS тензор к
полученному выражению применяется обратное преобразование
Фурье, и получается оценка SFS тензора в разрешаемых полях
2
4
2
j
i
i j i j
u
u
u,u u u u u O
x x
.
Априорные оценки GLES модели проведены в [18], в
многочисленных работах (см. библиографию там же). Отметим, что в
результате применения разложений обратное преобразование Фурье
тензора Рейнольдса имеет четвертый порядок малости по величине
радиуса фильтра
4
i j
u u O
, и в данной модели не учитывается.
113
На практике модель оказывается неустойчивой (на что
указывает также и анализ), и в [18] в качестве гипотезы предложено
решать эту проблему добавлением диссипативного члена модели
Смагоринского. Так появляется смешанная модель. Эта процедура
приводит лишь к уточнению модели Смагоринского, в которой
гипотетически появляется возможность моделирования обратного
рассеяния энергии по каскаду.
Рациональная модель
Рациональная модель RLES [18] отличается от предыдущей
модели GLES тем, что в волновом пространстве при разложении
образа ядра фильтра вместо ряда Тейлора применяется рациональная
аппроксимация Паде, которая устойчива и совместима с процедурой
фильтрования по Гауссу. Преобразование Фурье выражения
i i
u G* u
приводит к
1
i i
u k u k
G k
. Для высоких волновых чисел имеет
место асимптотика убывания
0
G k
по экспоненциальному
закону. Поэтому возникает проблема обращения ядра. В качестве
простейшего приближения применяется поддиагональная
аппроксимация Паде вида
2
2
4 4
1 1
4
G k k O k
,
которая снова приводит к аппроксимации 4-го порядка
1
2
2
4 4
1 1
4
u k u O k
.
Аппроксимация флуктуации поля скорости принимает вид
2
2
4
i i
u u
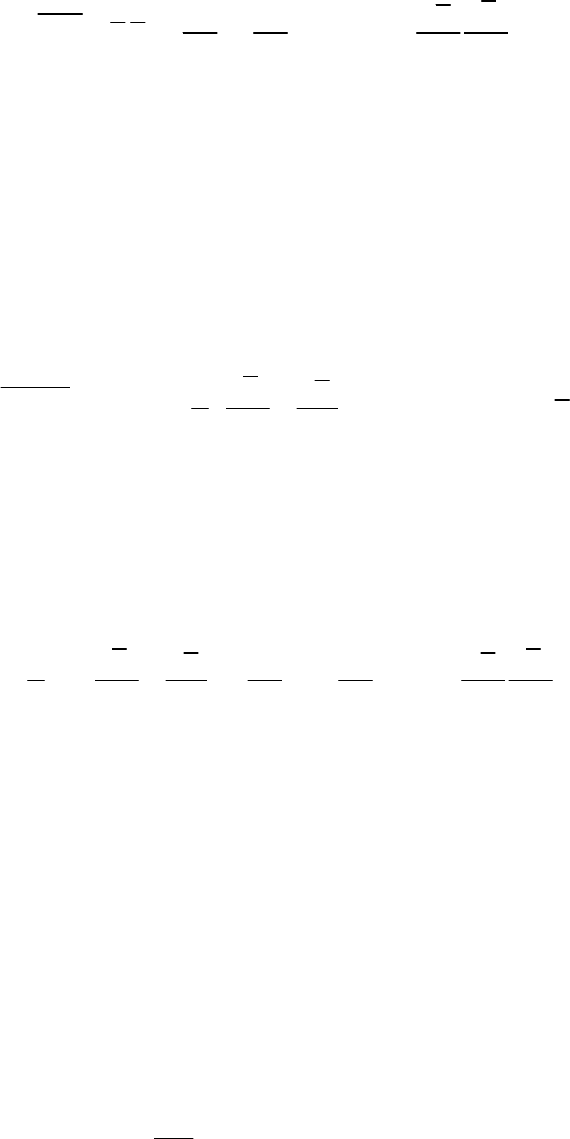
114
где
2
- оператор Лапласа.
Подстановка в SFS тензор и последующее применение обратного
преобразования Фурье приводит к замыканию
1
2 2
2 4
2 4
j
i
i j i j
u
u
u,u u u u u I O
x x
.
Данная модель опускает все члены порядка
4
O
, поэтому вклад от
тензора Рейнольдса также отсутствует. Однако учет дивергенции
рейнольдсова тензора считается важным, и поэтому он добавляется
через внедрение в модель вихревой вязкости
1
2
j
i
T
i j
u
u
u ,u
x x
, где
T T
u ,
Смешанная RLES на основе добавления модели вихревой
вязкости
T
принимает вид [80,81]
1
2 2
2 4
1
2 2 4
j j
i i
T
i j
u u
u u
u ,u I O
x x x x
Возможность моделирования обратного рассеяния в RLES модели
обсуждается в [79].
Подфильтровая модель повышенного порядка HOSFS
В RLES модели разложение по волновым числам приводит к
аппроксимации порядка
2
O
для членов, составляющих тензор SFS
напряжений. При выводе RLES модели опущены все члены порядка
4
O
и по этой причине RLES модель замыкания также не содержит
вклада от корреляции
i
j
u u
. В [19] (см также [18]) предложена
подфильтровая модель повышенного порядка по радиусу фильтра
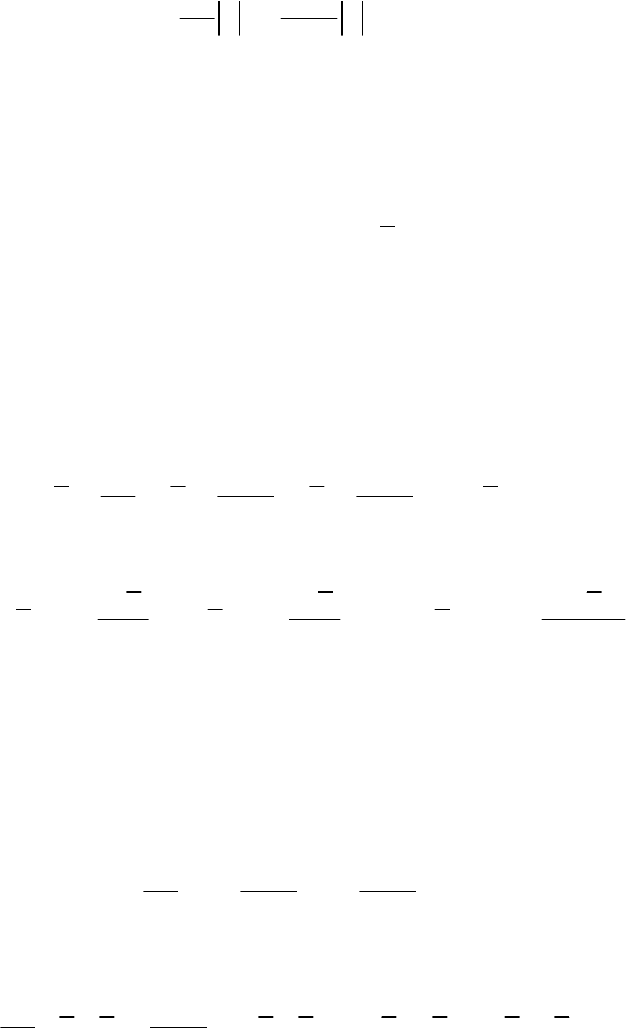
115
(HOSFS), которая использует асимптотическое разложение в
волновом пространстве более высокого порядка, чем RLES, а именно,
рациональную аппроксимацию Паде второго порядка
1
2 2 3
1 0 5
x
e x . x O x
.
Воздействие преобразования Фурье на ядро фильтра дает
аппроксимацию
1
2 4
2 4
6 6
1
24 1152
G k k O k
Поэтому связь актуальной и фильтрованной величин в спектральном
пространстве приводит к
1
i i
u k G k u k
В итоге после обратного преобразования Фурье в физическом
пространстве получаем соответствующую связь фильтрованных и
нефильтрованных полей
2 4 4
2 4 2 2 6
24 1152 1152
l m
i i i i i
u u u u u O
Здесь
2 4 4
3 3 3
2 4 2 2
2 4 2 2
1 1 1
i i i
i i l m i
m, l ;
l m
m l
u u u
u , u , u
x x x x
Подстановка этого выражения в тензор SFS напряжений после весьма
громоздких преобразований [19] приводит к окончательному виду
SFS модели для замыкания
1
2 4 4
2 4 2 2
24 1152 1152
l m
ij
I
2 4
3 2 2 3
4
12 1152
︵
︶
i j i j i j i j
u u u u u u u u

116
4
2 2 2 2
4
2 2 2
1152
︵
︶
m l i m j l i m j m l i m l j l i m l j
u u u u u u u u
Применение модели в реальных вычислениях выглядит
чрезвычайно затратным. В [18] высказывается предположение о
возможности локального применении модели вследствие быстрого
затухания волновой асимптотики с целью повышении экономичности
общего алгоритма. Проблемой является также реализация условий
для модели на твердых границах. В [18] также приводятся результаты
тестирования GLES, RLES, HOSFS моделей для частного случая
монохроматической волны при использовании пространственных
периодических граничных условий. Сопоставление на выбранных
волновых числах указывает на превосходство модели HOSFS .
4.7 Моделирование обратного энергетического каскадного
процесса
В среднем в турбулентности энергия передается от больших
масштабов к малым масштабам и в конце диссипирует в тепло.
Однако в определенные моменты времени в течении локально
возникает обратный процесс рассеяния энергии от малых вихрей к
большим вихрям. Явление обратного рассеяния энергии не
противоречит общей концепции энергетического каскада. Обратный
процесс является существенно менее интенсивным в сравнении с
прямым процессом, и его роль в динамике турбулентности еще не
вполне понятна [141,153].
Рассмотренные выше модели подсеточных напряжений в
основном отражают основной каскадный процесс – процесс прямого
рассеяния энергии от больших к малым вихрям. Моделирование
обратного процесса является деликатной процедурой в связи с низкой
интенсивностью потока энергии, и требует добавления специального
энергетического источникового члена в интегрируемые уравнения.

117
Обычно используются два подхода к построению моделей
обратного процесса рассеяния [68,69,106,153]:
- добавление стохастического члена на основе случайных переменных
и информации содержащейся в разрешаемых масштабах;
- модификация турбулентной вязкости, которая ассоциируется с
прямым каскадным процессом рассеяния; в этом случае обратный
каскадный процесс моделируется вкладом эффективной
отрицательной турбулентной вязкости, которая должна быть
добавлена к эффективной турбулентной вязкости, участвующей в
общем каскадном процессе.
Существуют оценки Kerr и др.[88], выполненные на основе
анализа взаимодействия тензоров скорости и завихренности
фильтрованных и неразрешаемых полей, которые указывают на
определяющую роль вклада от произведения
u
в обратный
процесс рассеяния.
Piomelli и др. [136] выполнили DNS анализ переходных и
турбулентных сжимаемых течений в каналах, а также изотропной
турбулентности. Во всех рассмотренных течениях обнаружилось до
50% ячеек, в которых в определенные моменты регистрировалась передача
энергии по обратному каскаду при использовании фурье-фильтра, и
несколько менее при использовании гауссового или коробчатого
фильтров. Таким образом, в настоящее время принята концепция
LES, которая должна включать обратный каскадный процесс
рассеяния энергии.
Простые модели вихревой вязкости в стандартной форме
являются чисто диссипативными и поэтому не могут включать
передачу энергии по обратному каскаду. Примером является модель
Смагоринского. Ее неспособность включить обратное рассеяние
является одним из источников относительно низкой точности во
многих практических течениях. Для включения обратного рассеяния
часто используется ее динамическая версия, предложенная Germano
[129]. Однако ввиду неустойчивости динамическая версия модели
Смагоринского обычно используется с ограничителем коэффициента
S
C
. Кроме того, ряд авторов высказывают сомнения относительно
содержания механизма обратного рассеяния в динамической модели.
118
В целом реализация механизма обратного рассеяния возможна,
если анализ указывает на наличие недиссипативных добавочных
членов в модели. Такие модели относятся к классу детерминистских
статистических моделей, и могут быть реализованы как в
спектральном (например, [27]), так и в физическом пространствах
(например, упомянутая версия Germano, или Ghosal [62])
Существуют модели LES, которые включают в неразрешаемые
напряжения механизм обратного рассеяния естественным путем.
Такие модели должны содержать механизм случайного процесса в
моделировании неразрешаемых напряжений. При этом случайный
процесс моделируется на основе функции плотности вероятности
(PDF) или функции плотности фильтра (FDF) [68,69].
В качестве промежуточного подхода между детерминистским
статистическим подходом и стохастическим подходом существуют
модели, которые содержат добавочные члены для имитации
случайного процесса, в частности применяется модель случайного
процесса Ланжевена. Одной из первых здесь разработана модель
замыкания Magagnato-Gabi [113,114] (см. гл.6).

119
5. ПРОБЛЕМА ГРАНИЧНЫХ УСЛОВИЙ В LES.
СЛУЧАЙ АНИЗОТРОПНОЙ ТУРБУЛЕНТНОСТИ
Хорошая обусловленность задачи для осредненных уравнений
Навье-Стокса опирается на локализацию граничных условий, которые
учитывали бы непроницаемость границ и некоторое проскальзывание
вдоль границ с потерей энергии на преодоление сопротивления при
скольжении:
0
u n
и
ˆ
0
i i
u n
на границе
Здесь
, , 1,2
i
n i
- орты-векторы нормали и касательной в
соприкасающейся плоскости;
- коэффициент скольжения;
ˆ
-
тензор напряжений.
Если для заданного числа Рейнольдса коэффициент
при
0
, то эти условия соответствуют прилипанию, при
0
и
Re
для фиксированного радиуса фильтра
условие
эквивалентно скольжению без трения.
По оценкам Максвелла (см.[18]) характерные значения для
коэффициента скольжения составляют
Re
O L , однако
u
зависит от скорости вблизи границы, и поэтому предположение о
постоянстве
является ограничением.
Способы вычисления
с позиций аппроксимации пограничного
слоя на основе фильтрованных величин обсуждаются также в [47,
83,154]. Данный подход позволяет учесть нестационарные пульсации
u
вблизи стенки. Суть формулировки граничных условий для LES
состоит в определении такого коэффициента трения, который
допускал бы флуктуации на стенке.
По замечанию [18], трудности моделирования LES отмечаются в
пристенной турбулентности, еще большие трудности возникают при
моделировании взаимодействия течения и стенки. Например, если для
уравнения переноса завихренности
rot
u
(гл.2)

120
2
, , 1,2,3
i i i i
j j
j j j j
u
u i j
t x x x x
задать нулевые начальные и граничные условия, то решение будет
тождественно равным нулю. Это подтверждает известные
классические результаты о том, что завихренность в турбулентном
течении исходит от границ. В практических случаях задание значения
завихренности на стенке является проблемой, и поэтому уравнение в
форме переноса завихренности не используется в расчетах.
5.1 Законы пристенной турбулентности в традиционных
RANS моделях и их применение к LES
Как было замечено в предыдущем разделе, в общем случае
пристеночная LES модель должна сводиться к DNS модели на стенке.
Однако подобная модель чрезвычайно затратна, и поэтому
используются упрощенные подходы, в частности, заимствованные из
RANS моделей.
Классический подход, берущий начало в модели
K
, состоит в
уничтожении части пограничного слоя (см.[97]). Граничные условия,
аналогичные по структуре приведенным выше, ставятся на
искусственной границе, расположенной внутри области вблизи
стенки
u n f x
,
2
ˆ
0, 1,2
i i
u u u n i
.
Здесь
u
- скорость скольжения, которая входит в осредненный
профиль скорости пограничного слоя и называется законом стенки.
Тензор напряжений представляется в виде
ˆ
ˆ
T
p I S
В статистическом описании пограничного слоя выделяются
характерные области. Пусть
- толщина пограничного слоя;
