Солодов В.Г. Моделирование турбулентных течений. Расчет больших вихрей
Подождите немного. Документ загружается.

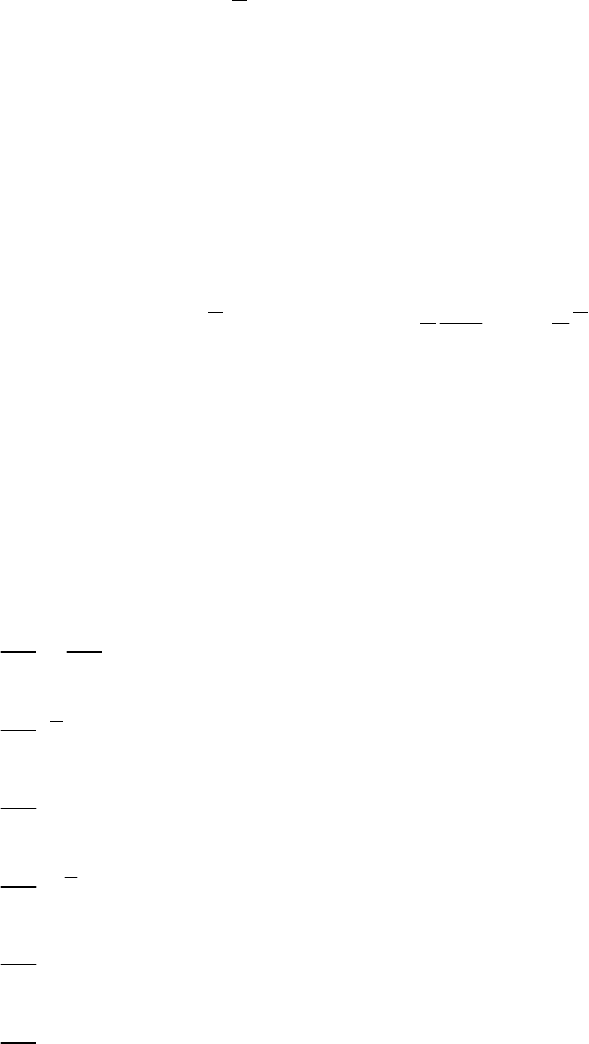
61
Величина
F
ij i
j
u u
аналогично рейнольдсовому аналогу
также является симметричным тензором турбулентных напряжений и
требует способа определения. Причина появления тензора – в
нелинейности конвективного оператора уравнений Навье-Стокса. В
соответствии с гипотезой Буссинеска о вихревой вязкости можно
записать
1 2
2
3 3
F
k
ij i T ij ij ij
j
k
u
u u S K
x
Сравнивая осреднение по Рейнольдсу и осреднение по Фавру,
можно отметить более краткую форму записи осредненного
уравнения неразрывности. Дополнительные члены уравнения энергии
имеют следующий физический смысл
j j
T
x x
- молекулярная диффузия тепла;
j
j
u h
x
- турбулентный перенос тепла;
ji i
j
u
x
- молекулярная диффузия кинетической энергии;
j
j
u K
x
- турбулентный перенос кинетической энергии;
i ji
j
u
x
- работа молекулярных сил трения;
F
i ij
j
u
x
- работа рейнольдсовых напряжений, осредненных по
Фавру
В целом, осреднение по Фавру приводит к более компактному
виду полных осредненных уравнений NS. Для уравнений динамики
несжимаемой жидкости осреднение по Фавру превращается в
осреднение по Рейнольдсу. Следует подчеркнуть, что
принципиальным недостатком данного подхода, так же как и
осреднения по Рейнольдсу, является действие осреднения сразу на все
масштабы турбулентных структур за время осреднения.

62
3.4 Осреднение уравнений Навье-Стокса с использованием
фильтра
Концепция фильтрования решений уравнений Навье-Стокса
основана на специальном ограничении решений уравнений NS,
связанном с выделением (разрешением) вихревых структур до
определенного масштаба малости. Концепция фильтрования в
конечном счете определяется размером сеточного разрешения, либо
интервалом времени. Не выделенные фильтром свойства решения
должны моделироваться некоторой специальной дополнительной
приближенной моделью.
Простейшая дискретная операция фильтрования вытекает из
представления центральной конечной разности в виде
1 1
i
i
x
i i
x
i
d
x x d
x dx
Последняя запись может быть интерпретирована как
фильтрующий оператор, ограничивающий разрешение вихревых
структур в уравнениях NS сеточным масштабом
.
Применение фильтрующего оператора к уравнениям NS
приводит к уравнениям, которые в дальнейшем называются
фильтрованными уравнениями Навье-Стокса (FNS).
Концепция фильтрующего оператора была известна до
разработки технологии LES в связи с применением к турбулентным
решениям уравнений Навье-Стокса теоретико-вероятностного
подхода [219].
Пропущенная через фильтр величина
(к которой применяется
фильтрующий оператор) будет называться отфильтрованной и
обозначаться чертой
1
i i
i i
x x
x x
x d G x, d

63
В простейшем случае весовая функция
1
G x,
называется
функцией фильтра, и
- есть размер ячейки фильтра, который в
дальнейшем будем называть отсекающим масштабом фильтра, а
c
k
- соответствующим волновым числом.
Функция фильтрования
G x,
отлична от 0, если
x
и
близки.
Таким образом, параметр, входящий в уравнения NS, может быть
представлен в виде
,
,
Рассматривается также обобщенный оператор фильтра,
действующий в пространстве и времени
3
x , G x ,t d d
где ядро
G
ассоциируется с масштабами отсечения в пространстве
и времени.
Важнейшие свойства фильтрующих операторов [18].
1. Ограниченность
3
, 1
G x t d d
2. Линейность
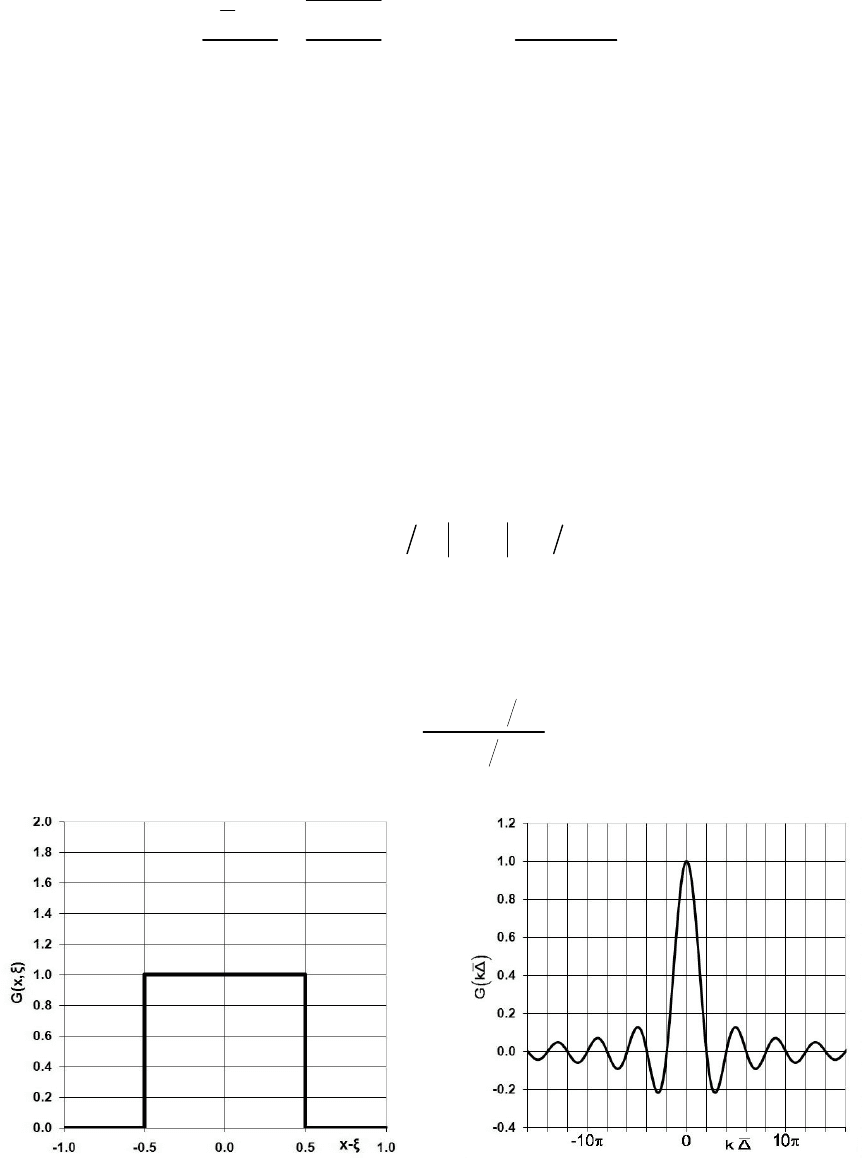
2. Коммутативность относительно оператора производной
i i
x x
64
Последнее свойство выполняется не для всех фильтров [141]. При
дифференцировании соотношения, определяющего операцию
фильтрования для пространственной координаты
x
, получается
x x G x
,t d
x x x
,
поэтому операции фильтрования и дифференцирования коммутируют
только для однородных по пространству фильтров (см. обсуждение
ниже).
Другие свойства операторов фильтрования можно встретить,
например в [141,18].
Существуют три наиболее употребительных фильтрующих
функции (см. например [18]):
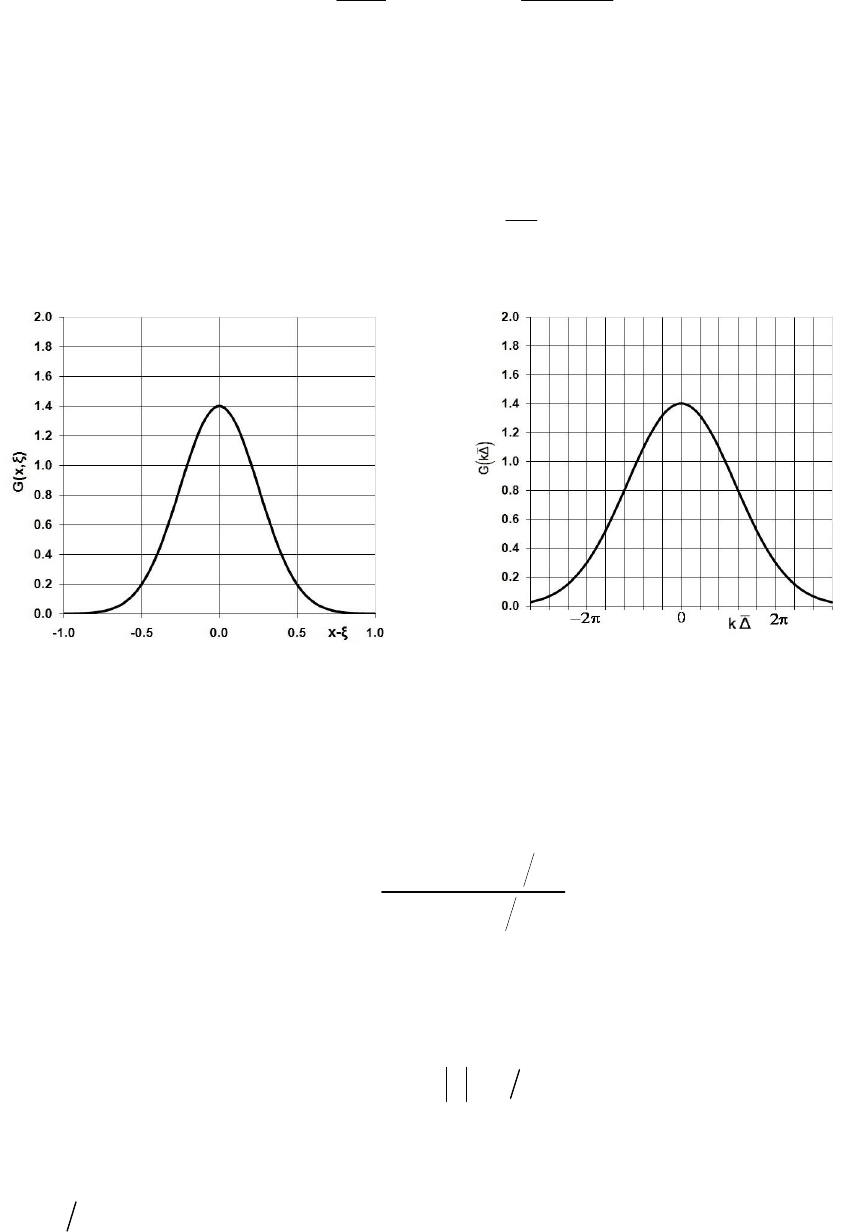
а) прямоугольный или «коробчатый» фильтр в физическом
пространстве (рис. 3.3а)
1 2
0
, x
G x,
,
в спектральном пространстве (рис. 3.3б)
2
2
sin k
G k
k
Рис.3.3 Прямоугольный или «коробчатый» фильтр
а) в физическом пространстве; б) в спектральном пространстве
65
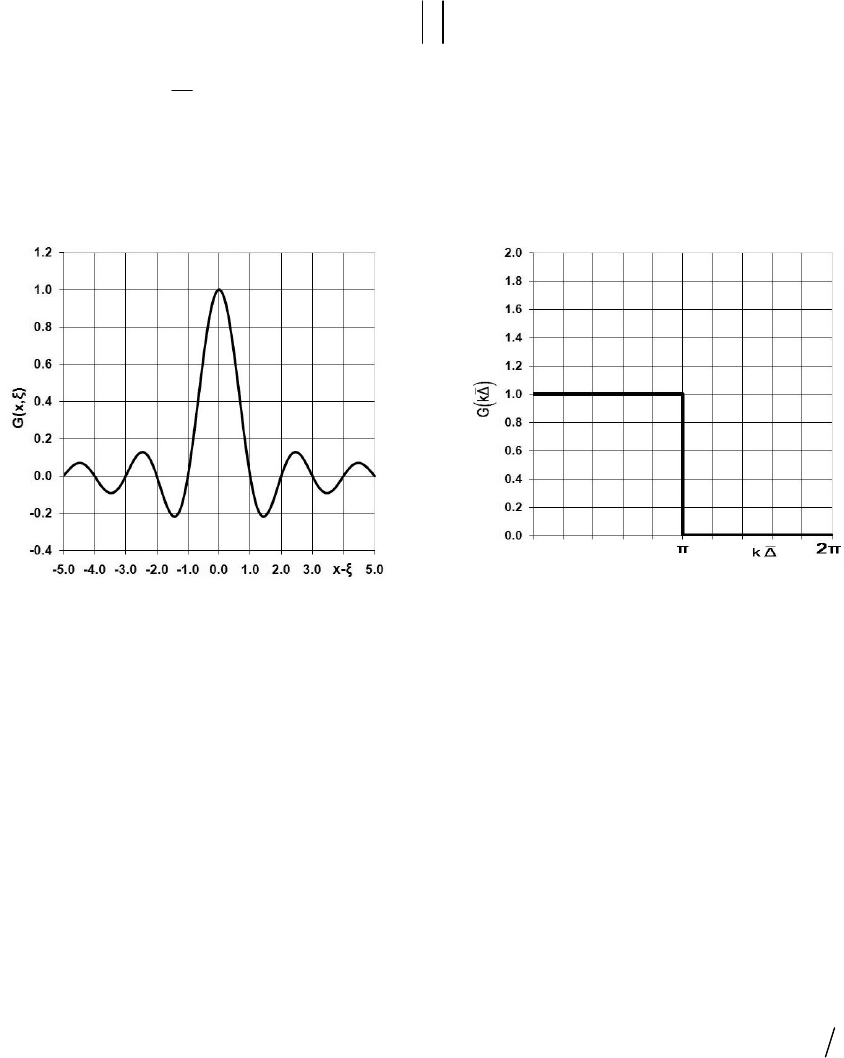
б) гауссов фильтр в физическом пространстве (рис. 3.4а)
2
3 2
2 2
6
6
/
x
G x, exp
.
в спектральном пространстве (рис. 3.4б)
2
2
24
k
G k exp
Рис.3.4 Гауссов фильтр
а) в физическом пространстве; б) в спектральном пространстве
в) спектральный или отрезающий фильтр (рис. 3.5а)
sin x
G x,
x
.
в спектральном пространстве(рис. 3.5б)
1
0
, k
G k
Здесь
c
k
является отсекающим волновым числом.
66
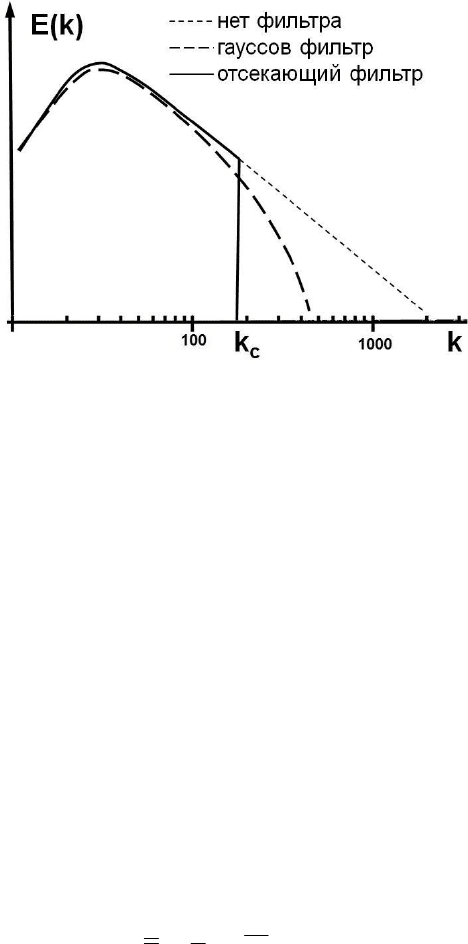
Пульсационная составляющая для разных фильтров, вообще
говоря, различна. Это отчетливо демонстрирует рис.3.6, на котором
представлен энергетический спектр фильтрованных зависимостей
кинетической энергии.
Таким образом, спектральный фильтр уничтожает все Фурье
моды данного волнового числа
k
большие, чем волновое число
отсечения
c
k
, но не воздействует на низкие моды волнового
числа, поэтому иногда говорят об отсечении больших волновых чисел.
Однако данный фильтр не локален в физическом пространстве.
Рис.3.5 Спектральный фильтр
а) в физическом пространстве; б) в спектральном пространстве
«Коробчатый» фильтр по свойствам противоположен
спектральному фильтру. Только гауссов фильтр компактен, локален
как в физическом, так и в спектральном пространствах.
Примеры и обсуждение свойств фильтров, отфильтрованных
случайных величин, и остаточных членов можно также найти у Роре
[141] для разных случаев фильтров (см. также по этому поводу [18]).
Фильтры, введенные в одномерной области, могут быть легко
обобщены на однородные и изотропные трехмерные фильтры,
например, «коробчатый» фильтр превращается в сферу радиуса
2
в
физическом пространстве.
Случай неоднородных и анизотропных фильтров
рассматривается в [153] в связи с проблемой моделирования
граничных условий на твердых стенках.
67
Рис.3.6 Энергетический спектр фильтрованных и нефильтрованных
решений для отсекающего и гауссовского фильтров с одинаковым
отрезающим волновым числом
c
k
(по [153])
Основная теорема теории аппроксимации фильтрования
(Н.Nyquist) связывает точность отсечения с качеством фильтрования.
Частота Найквиста равна половине частоты дискретизации. Таким
образом, при дискретизации возмущения полезную информацию о
разрешении будут нести только частоты ниже частоты Найквиста.
Разница между осреднением по Рейнольдсу и операцией
фильтрования заключается в том, что применяемые операторы не
удовлетворяют правилам Рейнольдса
, 0
.
Среди фильтров различают [153]:
-аналитические представления для фильтров, которые собственно
используются для фильтрования уравнений Навье-Стокса;
-фильтры, ассоциирующиеся с размерами вычислительной сетки; в
этом случае частота Найквиста ассоциируется с частотой отсечения;
-подходы к фильтрованию (например [161,162,112], Shih),
основанные на применении времениподобных фильтров;
Наличие и размер фильтра определяются также и порядком
применяемой аппроксимации дифференциальных операторов,

68
которая модифицирует в основном пульсационные моды высоких
частот.
Качество фильтрования также связано с качеством модели
подсеточных напряжений; именно, конкретный вид оператора
фильтра используется при моделировании подсеточных напряжений.
Реальное фильтрование в LES вычислениях определяется рядом
факторов [141,18,153 и др.], которые доминируют в практических
вычислениях.
Выбор вычислительного разбиения с сеточным размером
x
определяет максимальное разрешение в вычислениях согласно
теореме Найквиста (см. выше).
Идеальный (теоретический) фильтр, который, будучи применен
к точному решению уравнений Навье-Стокса, сглаживает решение и
выделяет пульсации, проходящие через этот фильтр, с характерной
отсекающей длиной
.
Численный фильтр определяется порядком аппроксимации
применяемого численного метода для интегрирования NSE. Именно,
численные методы неравномерно выделяют частоты
аппроксимируемого решения, так что большая погрешность
воздействует на более высокие волновые числа. Поэтому методы
очень высокого порядка точности, разрешающие соответственно
высокие волновые числа, не нуждаются в специальных моделях
подсеточных напряжений. В этой связи существует направление в
теории и практике LES, именуемое ILES – или неявное LES, и
основанное на применении схем очень высокого порядка
аппроксимации.
Кроме того, численный фильтр опирается на размер и
возможную анизотропию сеточного представления расчетной
области. В литературе, посвященной LES методологии,
применительно к неразрешающим напряжениям различаются понятия
подфильтрового (SFS) и подсеточного (SGS) масштабов. При этом
предполагается, что эти масштабы (радиус фильтра, либо сеточный
размер) различаются, хотя на практике чаще всего совпадают. В
дальнейшем, где это не принципиально, используется SGS
терминология.

69
3.5 Фильтрованные уравнения Навье-Стокса (FNS)
Пространственное фильтрование применяется к уравнениям
Навье-Стокса для отсечения малых турбулентных масштабов в
решениях.
Применение операции фильтрования к уравнениям Навье-
Стокса для случая декартовой системы координат и несжимаемой
среды независимо от выбора фильтра приводит к фильтрованным
уравнениям вида
0
i
i
u
x
,
2
1 1 2 1
2
3
i
i j ij kk ij i
j i j i
u p p
u u S S u
t x x x x
.
Данные FNS уравнения описывают пространственное и
временное поведение больших энергосодержащих масштабов
движения. Нелинейный конвективный член вызывает появление
тензора подсеточных напряжений
SGS
ij i j i j
u u u u
,
конкретный вид которого определяется видом выбранного фильтра.
Тензор подсеточных напряжений в корректно отфильтрованных
NS уравнениях является единственным членом, который несет в себе
информацию о свойствах ядра фильтра, однако будучи
приближенным (в силу своей модельности) по отношению к
идеальному, содержит погрешность моделирования, которая является
погрешностью фильтра.
3.6 Фильтрованные уравнения Навье-Стокса с осреднением
по Фавру
Консервативные переменные уравнений NS представляют собой
набор
i
, u , E
. Непосредственное фильтрование уравнений ведет к

70
фильтрованному набору
i
, u , E
. В соответствии с правилами
фильтрования по Фавру
i i
u u
, причем оператор, применяемый к
скорости, не является, вообще говоря, оператором используемого
фильтра.
В силу нелинейности уравнений NS значения полей давления и
температуры могут быть определены различным образом [153,74,75].
Обсуждение представлений можно также найти в работах [190,189].
Из наиболее распространенных представлений используется
синтетические давление
p
и температура
T
, которые выражаются
через фильтрованные величины
1 3p p
,
2
V
T C
.
В этом случае также модифицируется и уравнение состояния.
Употребляется также вариант набора переменных
i
ˆ
, u E
,
который дополняется фильтрованным давлением
p
и осредненной по
Фавру температурой
T
. В этом случае синтетическая полная энергия
определяется как
2
ˆ
E u
.
Фильтрованные по пространству уравнения FNS в декартовой
системе с осреднением по Фавру записываются в виде
i
i
u
t x
v
ij
v v
i i j ij ij
j i j j
ˆ
p
ˆ
u u u
t x x x x
2
2
3
ij kk ij
j
S S
x
,
