Солодов В.Г. Моделирование турбулентных течений. Расчет больших вихрей
Подождите немного. Документ загружается.


41
3
1
( ) ( )
8
i k r
u k u r e d r
Учет несжимаемости после преобразования Фурье уравнения
неразрывности приводит к ортогональности векторов
0
j j
k u
.
Уравнения Навье-Стокса для несжимаемой среды в
спектральном пространстве волновых векторов
1 2 3
, ,
k k k k
записываются в виде [219]
2
( , ) ( , )
i i
k u k t T k t
t
Нелинейный член
( , )
i
T k t
может быть представлен в форме
( , ) ( ) ( , ) ( , ) ( )
i ijm j m
T k t M k u p t u q t k p q dpdq
,
где
1
( ) ( ) ( )
2
ijm m ij j im
M k k P k k P k
;
2
( )
i j
ij ij
k k
P k
k
- оператор, проектирующий в плоскость,
ортогональную вектору
k
.
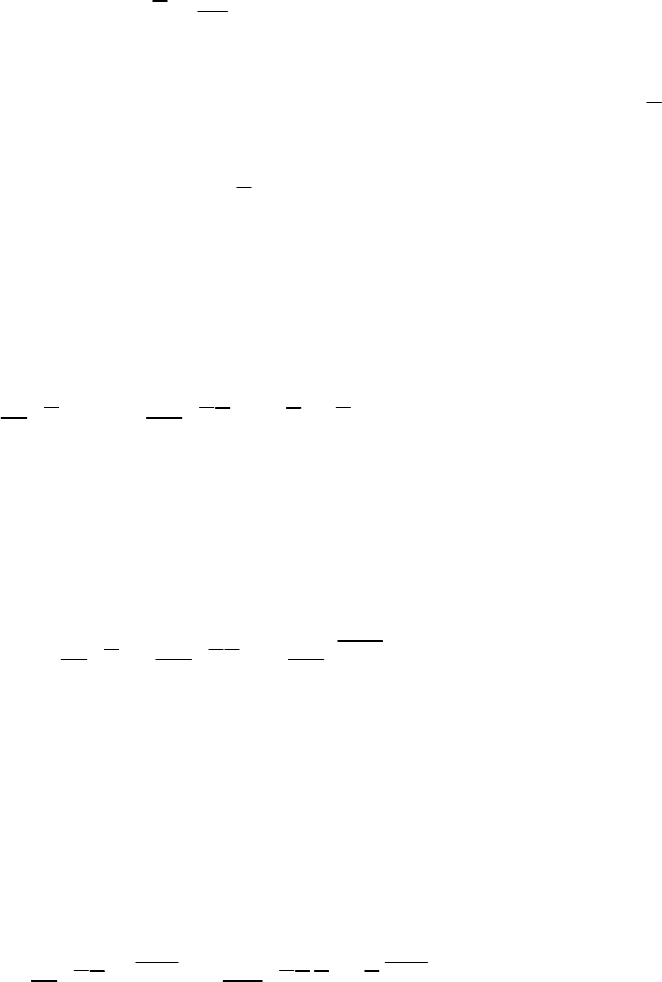
42
3. ОСРЕДНЕНИЕ УРАВНЕНИЙ НАВЬЕ-СТОКСА
3.1. Осреднение уравнений NS по Рейнольдсу и их способы
замыкания
Среднее от случайной величины, следуя Рейнольдсу, имеет вид
(гл.1):
1
o
o
t t
t
dt
t
.
Учитывая представление величин в виде суммы среднего
и
флуктуации
,
,
а также свойства операции осреднения (гл.1), получим уравнение
неразрывности с участием средних по Рейнольдсу
( ) ( ) 0
i i i i
i
u u u u
t x
.
После применения к уравнению неразрывности операции осреднения
по Рейнольдсу, получаем окончательно
( ) ( ) ( ) 0
i i i
i i
u u
t x x
.
При таком осреднении в уравнении неразрывности появляется
ненулевая дивергенция корреляционного момента пульсаций
плотности и скорости. Уравнения движения и энергии выглядят более
сложно [219]
( ) ( )
i ji i j i
j
u u u u u u
t x

43
,
, 1,2,3
i
ij i j i
j j
i j
p
u u u u u u
x x
i j
Для простейшего уравнения состояния
R
p T
уравнение энергии
представляется в виде
t t
t t i i
i
j j ji ji i i
i
e e
e e p p u u
t x
u u q q
x
или с учетом
0.5 , 0.5
t i i t t i i
e e u u h e p h u u
0.5 0.5 0.5 0.5
0.5 0.5 0.5 0.5
j j j j j j j j
j j j j j j j j i i
i
j j ji ji i i
i
e e u u u u u u u u
t
h h u u u u u u u u u u
x
u u q q
x
После применения к уравнению операции осреднения по
Рейнольдсу из вторых, третьих и четвертых моментов выносятся
средние. Средние пульсаций принимаются равными нулю. В итоге
осредненное по Рейнольдсу уравнение энергии принимает вид
0.5 0.5 0.5 0.5
0.5 0.5 0.5 0.5
j j j j j j j j
j j j j j j j j
e e u u u u u u u u
t
e e u u u u u u u u
t
0.5 0.5 0.5 0.5
0.5 0.5 0.5 0.5
i i j j i j j i j j i j j i
i
i i j j i j j i j j i j j i
i
hu h u u u u u u u u u u u u u
x
hu h u u u u u u u u u u u u u
x
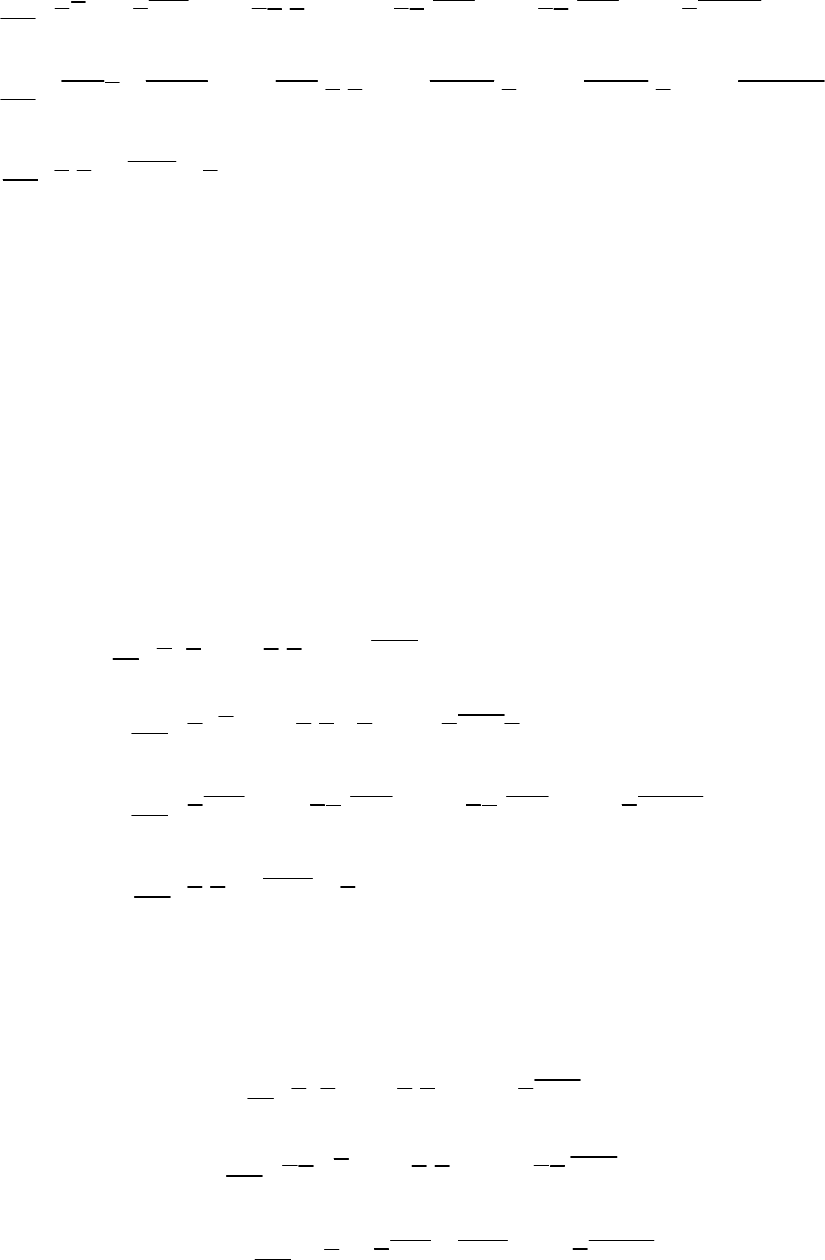
44
0.5 0.5 0.5 0.5
0.5 0.5 0.5 0.5
i i j j i j j i j j i j j
i
i
i i
i j j j j j j j j
i i i
i
j ji j ji i
i
hu h u u u u u u u u u u u u u
x
u h h u u u u u u u u u u u u u
x
u u q
x
Экспериментальные данные указывают на малость
турбулентных пульсаций плотности, и их влияние на структуру
пограничного слоя принято считать слабым (это положение известно
как гипотеза Морковина [131]). Эта гипотеза подтверждается
экспериментально для внутренних течений газов вплоть до чисел
M 5
. Исключение составляют течения со значительным
теплопереносом, свободные сдвиговые течения. В этой связи
пульсациями плотности в дальнейшем пренебрегаем
0.5 0.5
0.5 0.5
0.5 0.5 0.5
j j j j
j j i j j i
i
i j j j j j j
i i i
i
j ji j ji i
i
e u u u u
t
h u u u u u u
x
h u u u u u u u u u u
x
u u q
x
После преобразований окончательно получаем
0.5 0.5
j j j j
e u u u u
t
0.5 0.5
i j j i j j
i
u h u u u u u
x
0.5
i i j ji j j
i
i
q h u u u u u
x
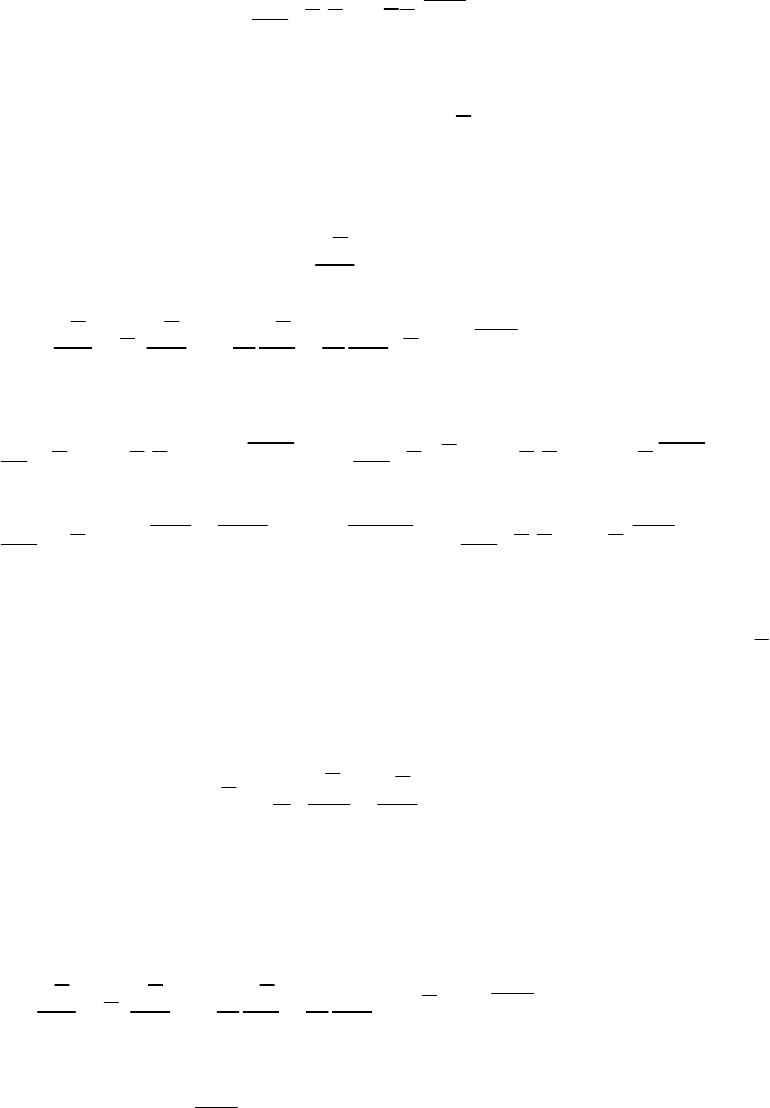
45
j ji j j
i
i
u u u u
x
Для случая несжимаемой жидкости
const
осреднение по
Рейнольдсу более естественно, и осредненные уравнения можно
записать в виде
0
i
i
u
x
,
1 1
, , 1,2,3
i i
j ji j i
j i j
u u p
u u u i j
t x x x
0.5 0.5 0.5 0.5
0.5
j j j j i j j i j j
i
i L i j ji j j j ji j j
i i
i i
e u u u u u h u u u u u
t x
q h u u u u u u u u u
x x
При применении закона вязкого трения Ньютона величина
ij
заменяется с использованием среднего значения тензора скоростей
деформаций
1
2
j
i
ij
i j
u
u
S
x x
и уравнение движения для несжимаемой среды приобретает вид
1 1
2 , , 1,2,3
i i
j ij i j
j i j
u u p
u S u u i j
t x x x
Величина
ij j i
u u
является симметричным тензором
рейнольдсовых (кажущихся или турбулентных) напряжений и
требует способа определения, т.е. замыкания системы уравнений. Его
появление – результат нелинейности конвективного оператора
уравнений Навье-Стокса.
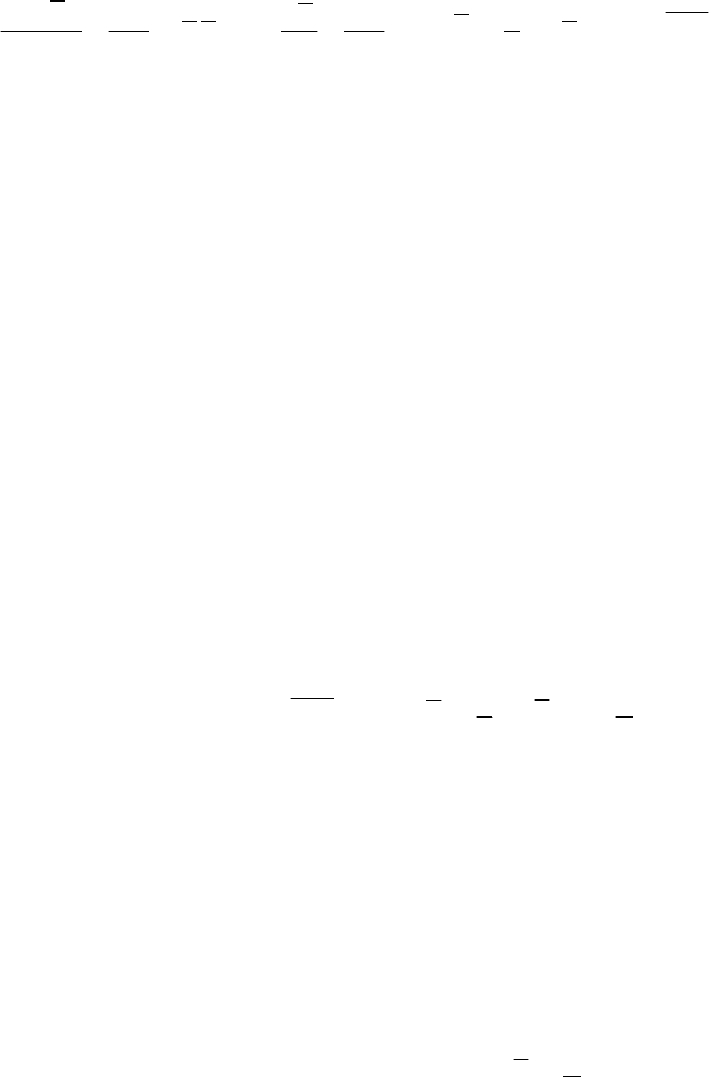
46
Дивергентная форма уравнения движения в случае сжимаемой
среды и выполнения гипотезы Морковина может быть представлена в
виде
1
2 , , 1,2,3
3
i
i j ij ij i j
j i j
u
p
u u S divu u u i j
t x x x
Следует заметить, что уравнения, осредненные по Рейнольдсу,
являются локальными, т.е. используют одноточечную статистику.
Тензор рейнольдсовых напряжений содержит шесть
неизвестных величин. Необходимость их определения порождает
обширный класс стандартных моделей. Среди них существуют как
модели прямого определения компонент тензора - так называемые
модели рейнольдсовых напряжений [48, 169,172,174], так и модели
вихревой вязкости, основанные на аналогии с гипотезой Буссинеска
[21] - на пропорциональности компонент тензора рейнольдсовых
напряжений и компонент тензора скоростей деформаций. Данная
гипотеза предполагает, что турбулентные сдвиговые напряжения
выражаются линейно через средний поток скоростей деформаций
аналогично ламинарному случаю
1 2
2
3 3
R
ij
турб i j T ij ij ij
u u S divu K
Гипотеза утверждает, что след тензора турбулентных напряжений
должен быть равен
2
K
. Это эквивалентно выполнению условия
равенства нулю второй вязкости. При этом подходе суммарный
тензор напряжений в уравнениях Навье-Стокса, осредненных по
Рейнольдсу, при условии несжимаемости примет вид
2
2
3
R
ij
лам ij турб L T ij ij
S K
.
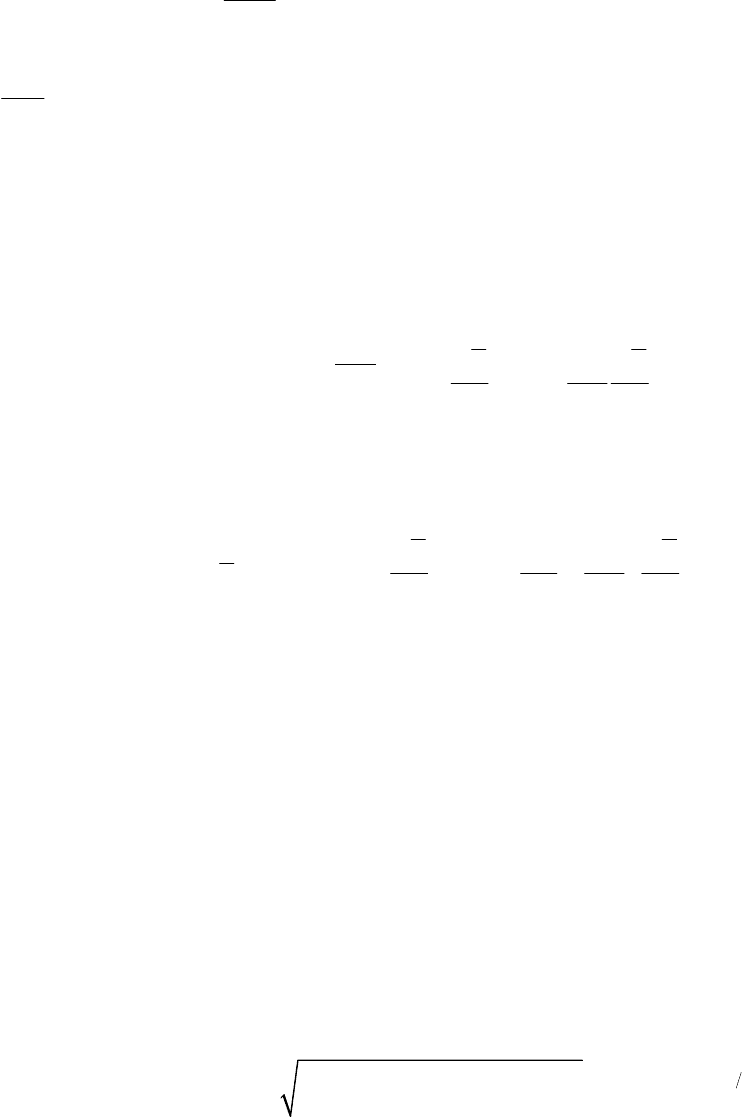
47
Величина
2
2 2
1 2 3
0.5 0.5K u u u u u
- кинетическая энергия
турбулентных флуктуаций скорости (иначе, половина свертки тензора
i j
u u
).
Аналогичное предположение делается относительно замыкания
диффузионного члена уравнения энергии. Величина корреляции
пульсаций скорости и энтальпии характеризует турбулентный
перенос теплоты и является турбулентным потоком теплоты
Pr
R
T
i T i T P
i T i
T T
h u C
x x
Поэтому суммарный тепловой поток представляется в виде
Pr Pr
T
i L T p
i T i
T T
q C
x x
,
где
Pr ,
T T
- соответственно турбулентные число Прандтля и
коэффициент теплопроводности.
3.2 Модели замыкания на основе коэффициента
турбулентной вязкости
Коэффициент турбулентной кинематической вязкости
T
определяется эмпирически, либо на основании анализа размерностей
через соотношение Прандтля-Колмогорова
2
2 2
1 2
1 2 3
0.5
T
const l u u u const l K
,
где
l
- масштаб турбулентных флуктуаций. В этом классе моделей
центральным вопросом является определение величин
,
l K
.
Семейство алгебраических моделей [192], основанных на
алгебраических соотношениях для
,
l K
, определяет эти величины из
достаточно простых соображений. Здесь наиболее плодотворной
оказывается гипотеза длины смешения Прандтля, на основе которой
48
были сделаны средние оценки эффектов поперечного градиента
скорости в сдвиговых течениях. Именно Прандтлю [143]
принадлежит определение скорости смешения через кинетическую
энергию пульсаций.
В дальнейшем, модель, основанная на гипотезе длины
смешения, подвергалась модификациям van Driest [187], Klauser [192]
и Klebanoff [91].
Следующим шагом в развитии идеи смешения стала
алгебраическая модель Cebeci-Smith [26], основная идея которой
заключается в двухслойном определении коэффициента
турбулентной вязкости на основе успешного объединения идеи пути
смешения во внутреннем слое и функции перемежаемости Клебанова
во внешнем слое.
Наконец, в 1978 в развитие заложенных идей была предложена
двухслойная модель Baldwin-Lomax [8] для случаев, когда толщину
вязкого подслоя и слоя смешения трудно определить. Несмотря на то,
что модель осталась по сути двумерной, как, впрочем, и все
предыдущие модели, здесь впервые была введена функция модуля
вектора завихренности.
В дальнейшем рассматривались также «неравновесные» версии
алгебраических моделей [192]. В целом алгебраические модели
удовлетворительно отражают весьма узкие классы течений, для
которых и были разработаны.
В отличие от алгебраических моделей вихревой вязкости более
сложные и поздние модели опирались на понятия
автокорреляционных моментов второго порядка для турбулентных
полей в рамках одноточечной статистики – кинетической энергии
турбулентных пульсаций
K
и скорости диссипации энергии
турбулентных пульсаций
.
Величины
,
K
и их производная – частота турбулентных
пульсаций
, вытекали из составленных при определенных
допущениях дифференциальных уравнений, из которых следовало
определять локальную величину вихревой вязкости.
Авторы [192,118] получают уравнение для кинетической
энергии турбулентных пульсаций
K
на основе свертки уравнения для
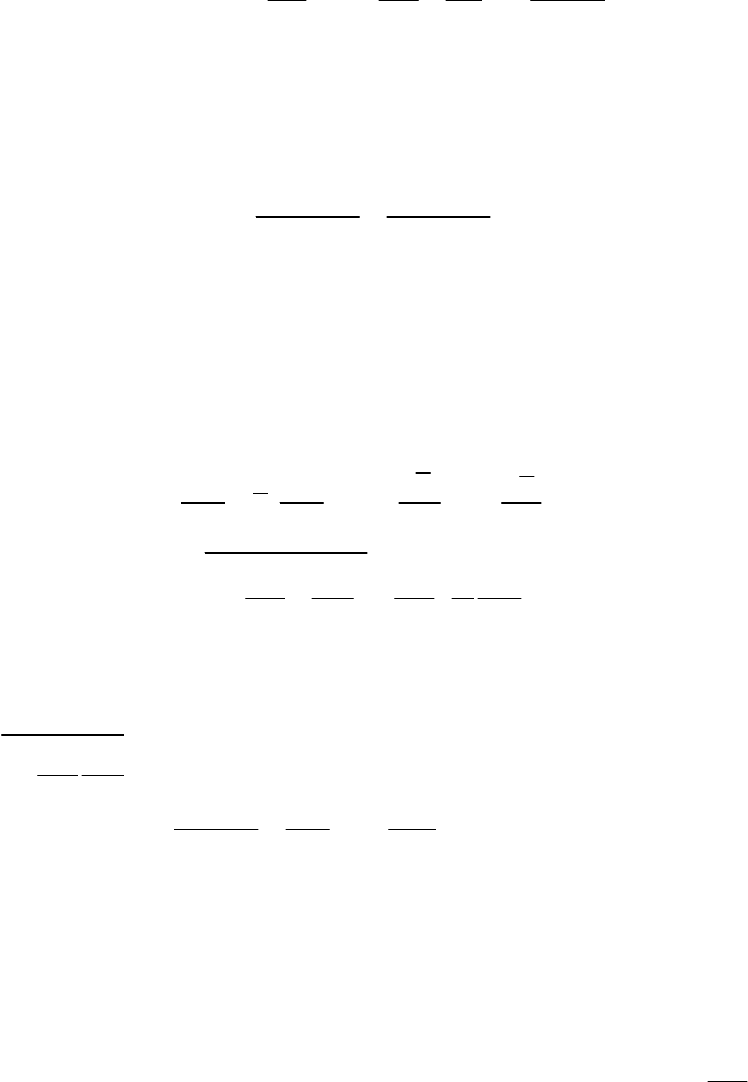
49
рейнольдсовых напряжений. Уравнение для рейнольдсовых
напряжений выводится из уравнений Навье-Стокса.
Для случая несжимаемого течения оператор Навье-Стокса
представляется в виде
2
( ) 0
i i i
i j
j i j j
u u p u
NS u u
t x x x x
.
Уравнение для рейнольдсовых напряжений вытекает из
преобразования временного среднего от выражения
( ) ( ) 0
j i i j
u NS u u NS u
.
После ряда предположений и громоздких преобразований
[192,118,219] получается дифференциальное уравнение переноса
рейнольдсовых напряжений
ij ij j
i
k ik jk ij
k k k
u
u
u
t x x x
j ij
i
ijk
j i k k
u
u
p C
x x x x
.
Здесь
2
j
i
ij
k k
u
u
x x
- скорость диссипации энергии турбулентных
пульсаций;
ijk i j k i jk j ik
C u u u p u p u
- момент пульсаций третьего
порядка.
В итоге, вследствие нелинейности уравнений Навье-Стокса
получается шесть уравнений для компонент тензора рейнольдсовых
напряжений и ряд дополнительных неизвестных.
Уравнение для кинетической энергии
K
вследствие
несжимаемости среды и гипотезы Буссинеска [21]:
2
ii i i
u u K
получается сверткой уравнения для тензора рейнольдсовых
напряжений

50
1
2
ij
i
k ik i i k k
k k k k
K u K
u u u u p u
t x x x x
.
На основании анализа экспериментальных данных и DNS
результатов приближенно считают [115], что
1
2
T
i i k k
K k
K
u u u p u
x
.
В результате получается окончательная форма уравнения для
турбулентной кинетической энергии
i
j ij T k
j j j j
K K u K
u
t x x x x
,
где вид величины
2
2
3
ij T ij ij
S K
записывается на основе
гипотезы Буссинеска.
В уравнении для кинетической энергии
K
стоковый член
представляет собой скорость диссипации турбулентной кинетической
энергии. Скорость диссипации по Тейлору следует из соображений
размерности [141]
3 2
ii
K l
.
Предположение
3 2
D
C K l
приводит к модели турбулентности
на основе уравнения для турбулентной кинетической энергии.
Константы модели
, ,
K D
C l
широко представлены для разных версий
модели [141,192]. Вихревая динамическая вязкость получается из
соотношения
1 2
T
K l
.
В последнее время появились модели, основанные на одном
уравнении, которые показывают хорошие результаты в предсказании
для частных классов течений – модель Baldwin-Barth, [7], и, особенно,
модель Spalart-Allmaras (SА)[167].
Модель SА имеет широкое применение в прямом и гибридном
моделировании больших вихрей, поэтому остановимся на ней
