Сметанина Р.Н. и другие. Теоретические основы электротехники

Подождите немного. Документ загружается.

Теоретические основы электротехники. Ч. 1. Постоянный и синусоидаль-

ный токи в линейных цепях: учебное пособие / Р.Н. Сметанина, Г.В. Но-

сов, Ю.Н. Исаев. – 3-е изд., испр. – Томск: Изд-во ТПУ, 2009. – 118 с.

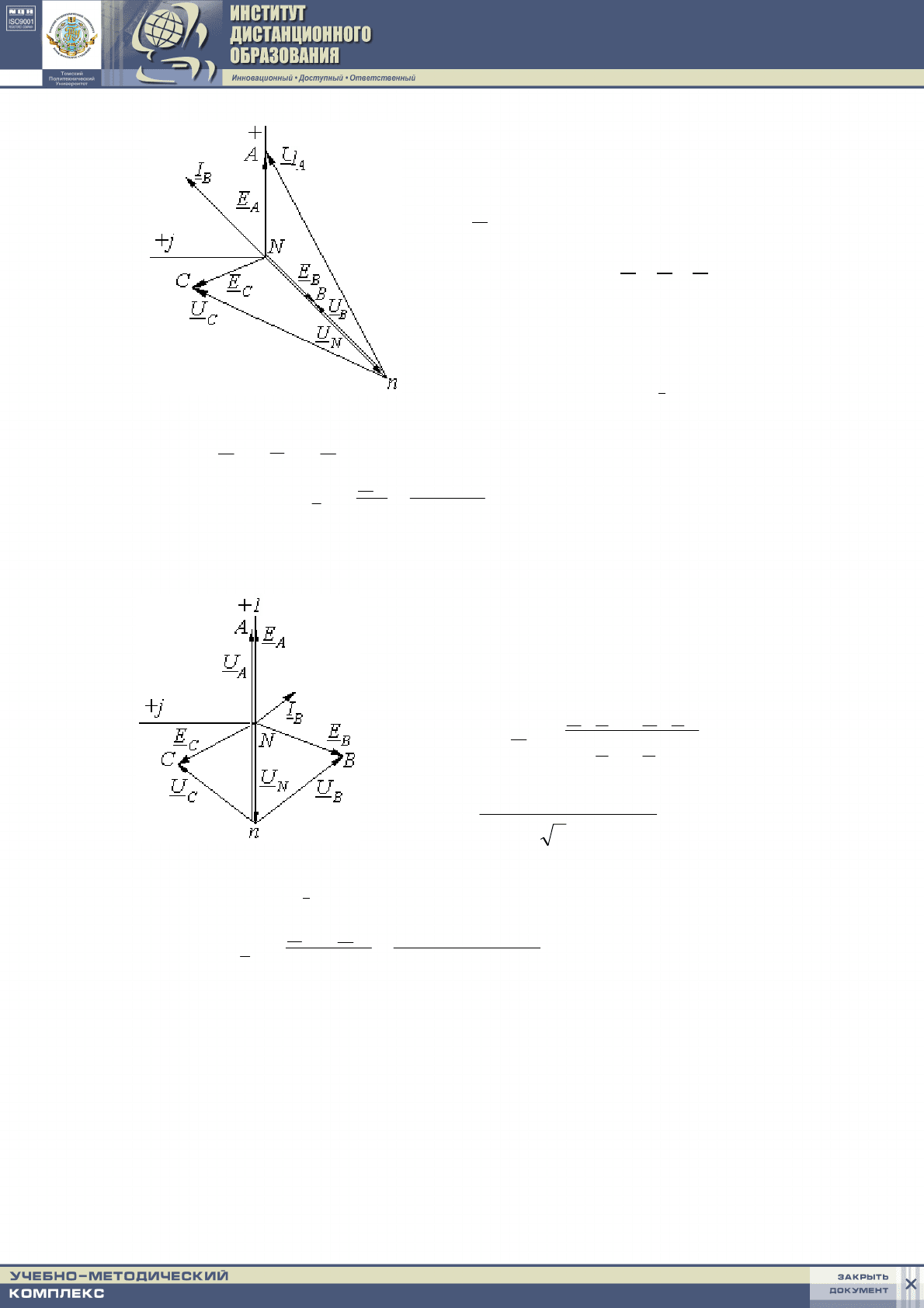
Построим диаграмму фазных ЭДС

генератора и найдем положение точки

n, отложив из точки N в масштабе век-

тор U

. Соединив точку n с точками A,

B, C, получим диаграмму фазных на-

пряжений нагрузки U

, U

Так как вольтметр включен между

точками N и n, он покажет 273 В:

= 273 B.

Определим ток I

, используя

обобщенный закон Ома (§ 3.4):

B173273100

60120120

ooo

jjj

eeeUEU =−=−=

−−

;

46,3

173

=== .

Показание амперметра равно 3,46 А.

2. Расчет при обрыве провода в

точке М.

Так как произошел обрыв фазы А,

сопротивление этой фазы стало равным

∞, следовательно, Y

= 0, тогда

B.6,136

210240

CCBB

−=

⎟

⎠

⎞

⎜

⎝

⎛

eeEY

YEYE

Показание вольтметра – 136 В.

Определим ток I

A45,2

136100

120

−

= .

Показание амперметра равно 2,45 А.

Результаты расчета наглядно продемонстрированы векторной диа-

граммой.

Теоретические основы электротехники. Ч. 1. Постоянный и синусоидаль-

ный токи в линейных цепях: учебное пособие / Р.Н. Сметанина, Г.В. Но-

сов, Ю.Н. Исаев. – 3-е изд., испр. – Томск: Изд-во ТПУ, 2009. – 118 с.

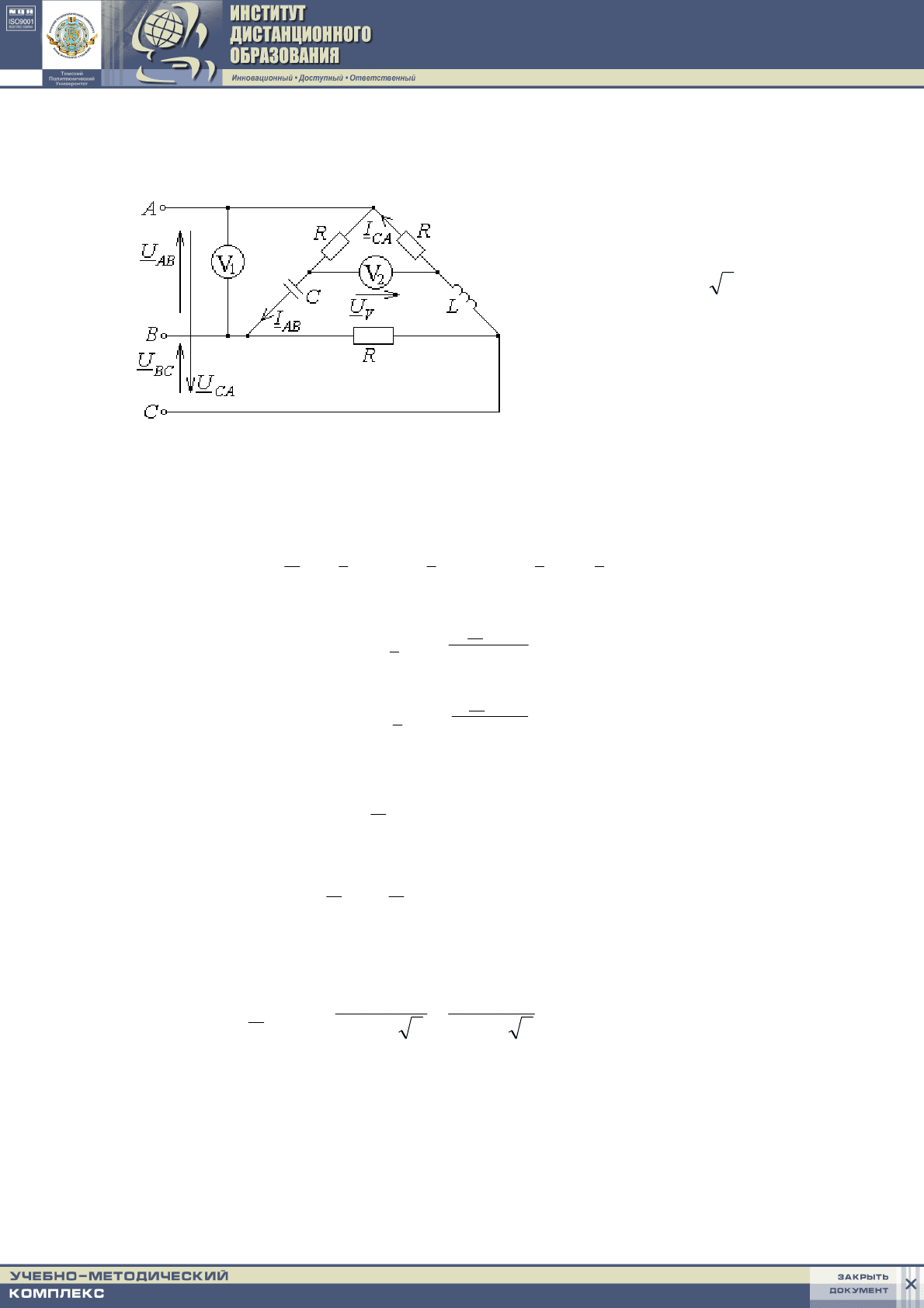
Пример 4

В заданной схеме система

линейных напряжений сим-

метрична и

3RXX

Определить показание

вольтметра V

, если известно

показание вольтметра

= 100 В (приборы элек-

тромагнитной системы).

Решение

Показание V

, т. е. напряжение U

можно определить по II закону

Кирхгофа:

(

)

ABCAABCA

IIRRIRIU

⋅

⋅= .

Учитывая соотношение (*), определим токи

;

jXR

−

СA

jXR

Приняв

UeUU

=⋅=

тогда

120

ABСA

eUeUU ⋅=⋅= ,

где

– линейное напряжение, соответствующее показанию V

отсюда

()

B.10043.025.045.025.0100

100

120

ejj

jRRjRR

⋅=+++⋅=

⎟

⎠

⎞

⎜

⎝

⎛

−

⋅

⋅=

Показание вольтметра V

равно 100 B.

Теоретические основы электротехники. Ч. 1. Постоянный и синусоидаль-

ный токи в линейных цепях: учебное пособие / Р.Н. Сметанина, Г.В. Но-

сов, Ю.Н. Исаев. – 3-е изд., испр. – Томск: Изд-во ТПУ, 2009. – 118 с.

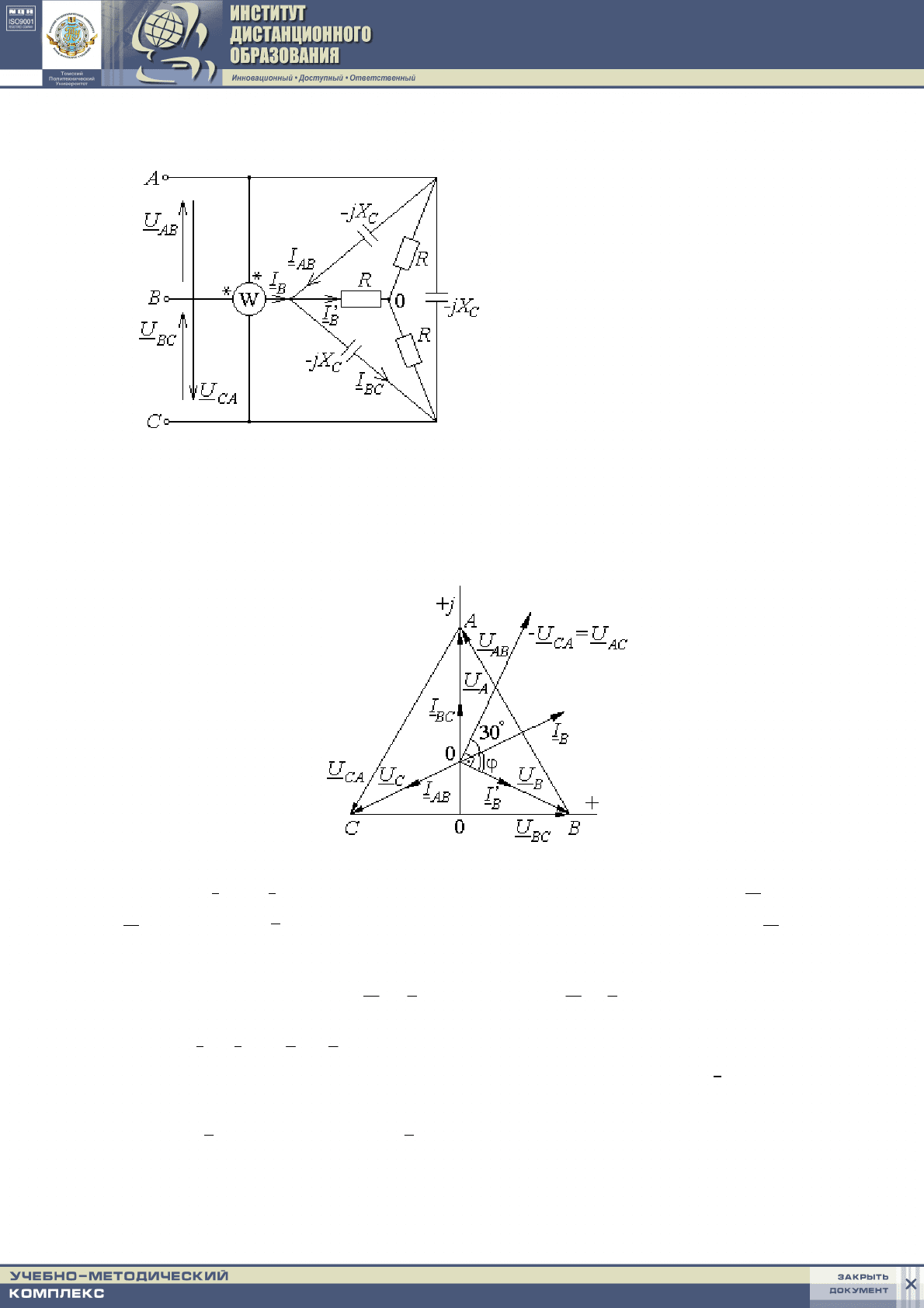
Пример 5

В заданной цепи система

линейных напряжений генера-

тора симметрична.

Все фазные токи одинако-

вые – по 1 А; X

= 100 Ом.

Определить реактивную

мощность трехфазной цепи.

Решение

Это симметричная трехфазная цепь, в ней емкости соединены «тре-

угольником», а резисторы «звездой».

Для расчета построим топографическую диаграмму напряжений, со-

вмещенную с лучевой диаграммой токов, только для узла В.

Токи I

и I

емкостные, они опережают свои напряжения U

на 90

. Ток

– активный, он совпадает по фазе с напряжением U

Показание ваттметра определится как

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

∧

BAC

cosRe IUIUIUP

Ток I

= I

II − .

Выбираем положительное направление осей. Ток I

мож-

но определить из векторной диаграммы, учитывая, что

60'

eII

−

⋅=+ ; А211

6012060

ooo

jjj

eeeI

−−

⋅=⋅−⋅= .

Теоретические основы электротехники. Ч. 1. Постоянный и синусоидаль-

ный токи в линейных цепях: учебное пособие / Р.Н. Сметанина, Г.В. Но-

сов, Ю.Н. Исаев. – 3-е изд., испр. – Томск: Изд-во ТПУ, 2009. – 118 с.

Ток I

– линейный, можно обозначить I

Построим на диаграмме U

= – U

Угол между векторами I

и U

равен 30

Линейное напряжение U

= U

= I

⋅X

= 100 B.

Тогда показание W: P

= 100⋅2 cos 30° = 3100 = 173 Вт.

Из векторной диаграммы видно, что

(

)

()

,sin

sin90sincos90cos

90cos30cos

лл

ллBAC

ϕ⋅⋅=

=ϕ⋅+ϕ⋅⋅=

=ϕ−⋅⋅=⋅⋅=

IUIUP

где угол ϕ – угол между фазным напряжением U

и током I

Для симметричной трехфазной цепи реактивная мощность

ϕ⋅= sin3

лл

IUQ , следовательно, чтобы определить реактивную мощ-

ность нашей цепи, а она симметричная, нужно показание ваттметра уве-

личить в

3 раза:

вар300331003 =⋅==

PQ .

Пример 6

В заданной трехфазной цепи система

линейных напряжений симметрична,

= 100 В , причем

XR 3= ; Ом10=

Определить токи в схеме, если:

1) произошел обрыв фазы в точке М;

2) оборвался линейный провод в

точке N.

Решение

1. Так как оборвался фазный провод в точке М, то I

= 0, тогда

A84,5

3,17

100

120

CAA

−

⋅=

⋅−

=−=−= ;

A84,5

120

eI ⋅=

;

A10

100

120

BCB

−

⋅=

⋅

−

== .

По первому закону Кирхгофа определим ток I

Теоретические основы электротехники. Ч. 1. Постоянный и синусоидаль-

ный токи в линейных цепях: учебное пособие / Р.Н. Сметанина, Г.В. Но-

сов, Ю.Н. Исаев. – 3-е изд., испр. – Томск: Изд-во ТПУ, 2009. – 118 с.

A3,151084,5

2,13930120

BCCAC

ooo

jjj

eeeIII ⋅=⋅−⋅=−=

−

Таким образом, линейные токи

A84,5

−

⋅= ; A10

−

⋅= ; A3,15

2,139

eI ⋅= .

При расчете приняли

лAB

UUU

= .

На основании I закона Кирхгофа I

+ I

= 0, подставим получен-

ные значения токов, убедимся в правильности расчета токов:

03,151084,5

2,1393060

=⋅+⋅+⋅

−−

ooo

jjj

eee .

Фазные токи

A;10

−

⋅= A.84,5

120

⋅=

2. В случае обрыва линейного провода в точке N I

= 0, тогда R и С

окажутся соединены последовательно, а с индуктивностью – параллель-

но, напряжение в фазе АВ не изменилось.

Определим токи по закону Ома:

A10

100

−=

⋅

;

103,17

100

СABС

jjXR

II ⋅=

−

== ;

A8,14510

1,10730

BCABBA

eejIIII

−

⋅=⋅−−=−=−= ;

A8,14

9,72

eI ⋅= .

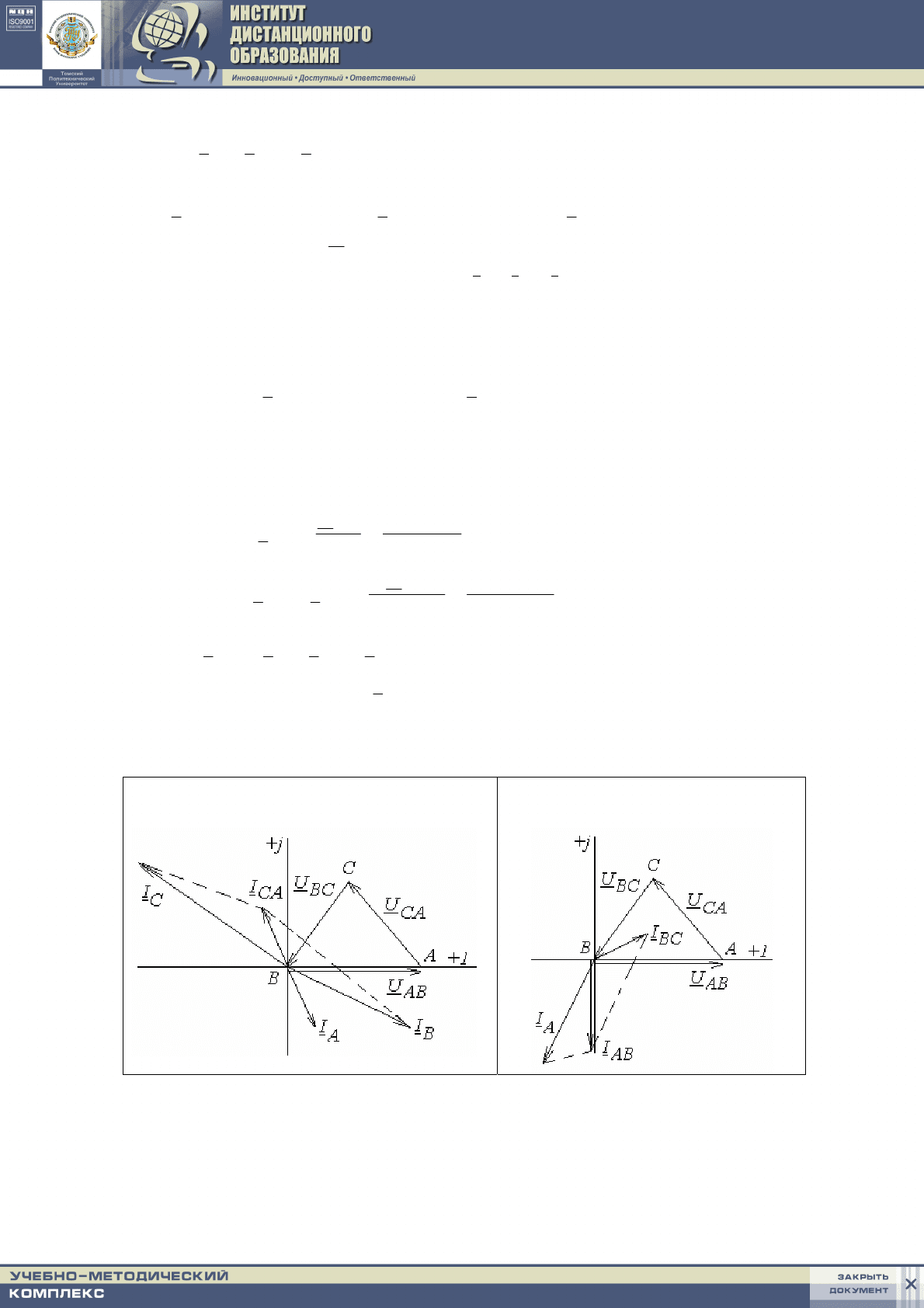
Расчеты проиллюстрированы векторными диаграммами.

Обрыв в точке М

Обрыв в точке N

Теоретические основы электротехники. Ч. 1. Постоянный и синусоидаль-

ный токи в линейных цепях: учебное пособие / Р.Н. Сметанина, Г.В. Но-

сов, Ю.Н. Исаев. – 3-е изд., испр. – Томск: Изд-во ТПУ, 2009. – 118 с.

Тема 7

ПЕРИОДИЧЕСКИЕ НЕСИНУСОИДАЛЬНЫЕ ТОКИ

И ЭДС В ЛИНЕЙНЫХ ЦЕПЯХ

На практике ЭДС, напряжения и токи обычно в большей или мень-

шей степени отличаются от постоянных или синусоидальных функций.

В машинных генераторах переменного тока, вследствие отличия кривой

распределения магнитной индукции вдоль зазора от синусоиды, кривые

наводимых в обмотках ЭДС отличаются от синусоидальных. В цепях,

содержащих элементы с нелинейными сопротивлениями, индуктивно-

стями или емкостями, даже при синусоидальных ЭДС возникают неси-

нусоидальные токи и напряжения.

Несинусоидальными токами и напряжениями называют токи и на-

пряжения, изменяющиеся во времени периодически по несинусоидаль-

ному закону.

7.1. Изображение несинусоидальных функций рядами Фурье

Явления, происходящие в линейных цепях при периодических, но

несинусоидальных ЭДС, напряжениях и токах, проще всего поддаются

исследованию, если кривые ЭДС, напряжений и токов разложить в три-

гонометрические ряды Фурье.

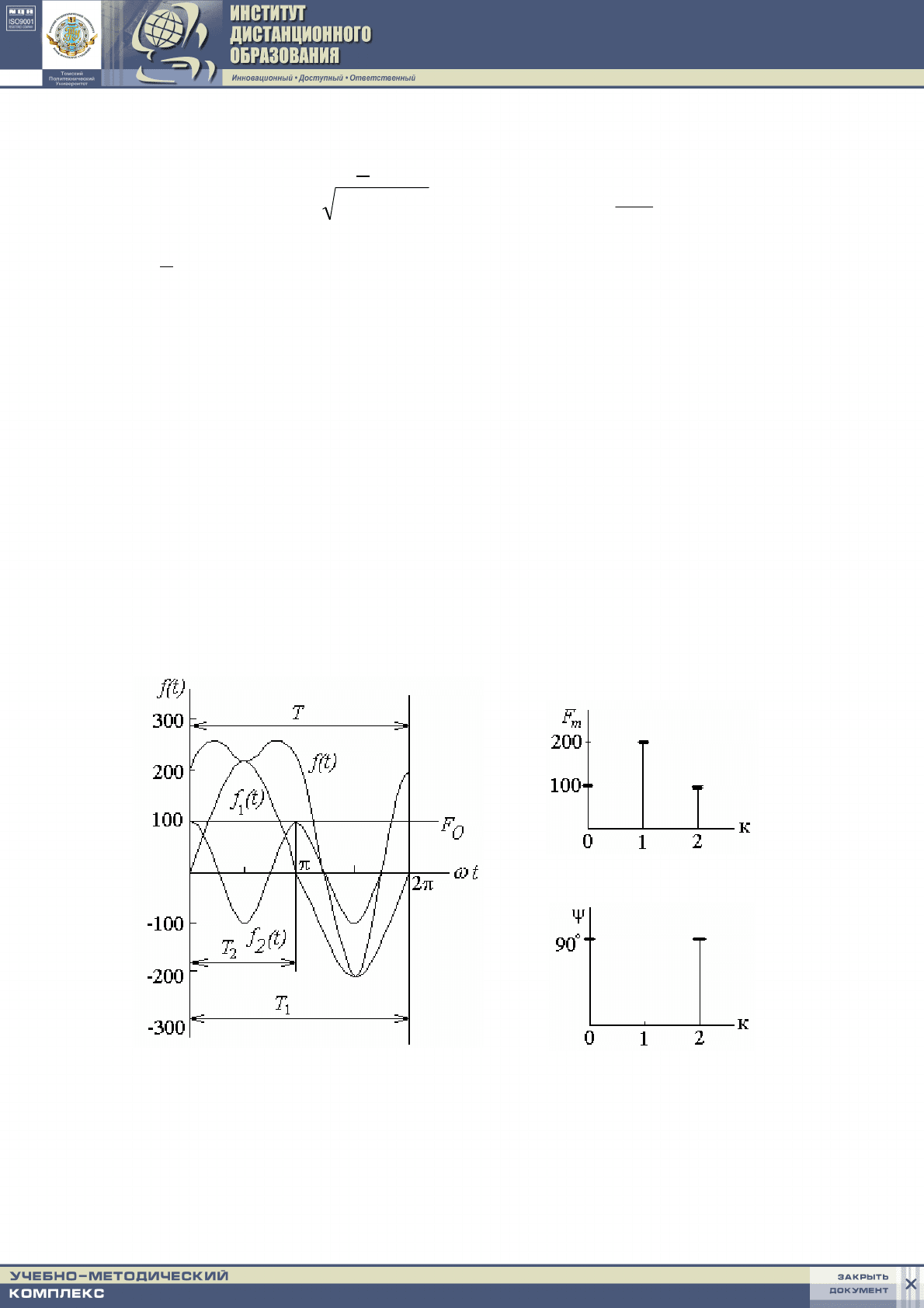
Любая периодическая функция f(t),

удовлетворяющая условиям Дирихле,

может быть разложена в тригонометри-

ческий ряд Фурье двумя формами:

1. f(ωt) = А

+ А

sin(ωt + ψ

) + А

sin(2ωt + ψ

) +... =

()

∑

∞

ψ+ω+

sin

kkm

tkAA

где k – номер гармоники; А

– постоянная составляющая или нулевая

гармоника; А

sin(ωt + ψ

) – первая или основная гармоника, Т

= Т;

sin(2ωt + ψ

) и т. д., т. е. при k > 1 – гармоники высшего порядка;

ω – основная частота; Т – период несинусоидальной функции.

2. f(ωt) =

∑

∞

ω+ω+

)cossin(

kmkm

tkCtkBA

Теоретические основы электротехники. Ч. 1. Постоянный и синусоидаль-

ный токи в линейных цепях: учебное пособие / Р.Н. Сметанина, Г.В. Но-

сов, Ю.Н. Исаев. – 3-е изд., испр. – Томск: Изд-во ТПУ, 2009. – 118 с.

Первая и вторая формы связаны соотношениями

= B

+ jC

= А

jψ

;

kmkmkm

CBA += ,arctg)180(

+=ψ

где А

– комплексная амплитуда “k” гармоники, причем

180 при рас-

чете

ψ учитывается при B

<0.

7.2. Понятие о дискретных (линейчатых) спектрах

Совокупность гармонических составляющих несинусоидальной пе-

риодической функции называют ее

дискретным частотным спек-

тром

Спектр можно характеризовать зависимостью А

(амплитудный

спектр) и ψ

(фазовый спектр) от частоты kω, причем фаза постоянной

составляющей условно принята равной 90° .

Пример

f(t) = 100 + 200sinωt + 100cos2ωt;

= 100; F

= 200; F

= 100; ψ

= 0; ψ

= 90°.

Линейчатые спектры

амплитудно-частотный

фазо-частотный

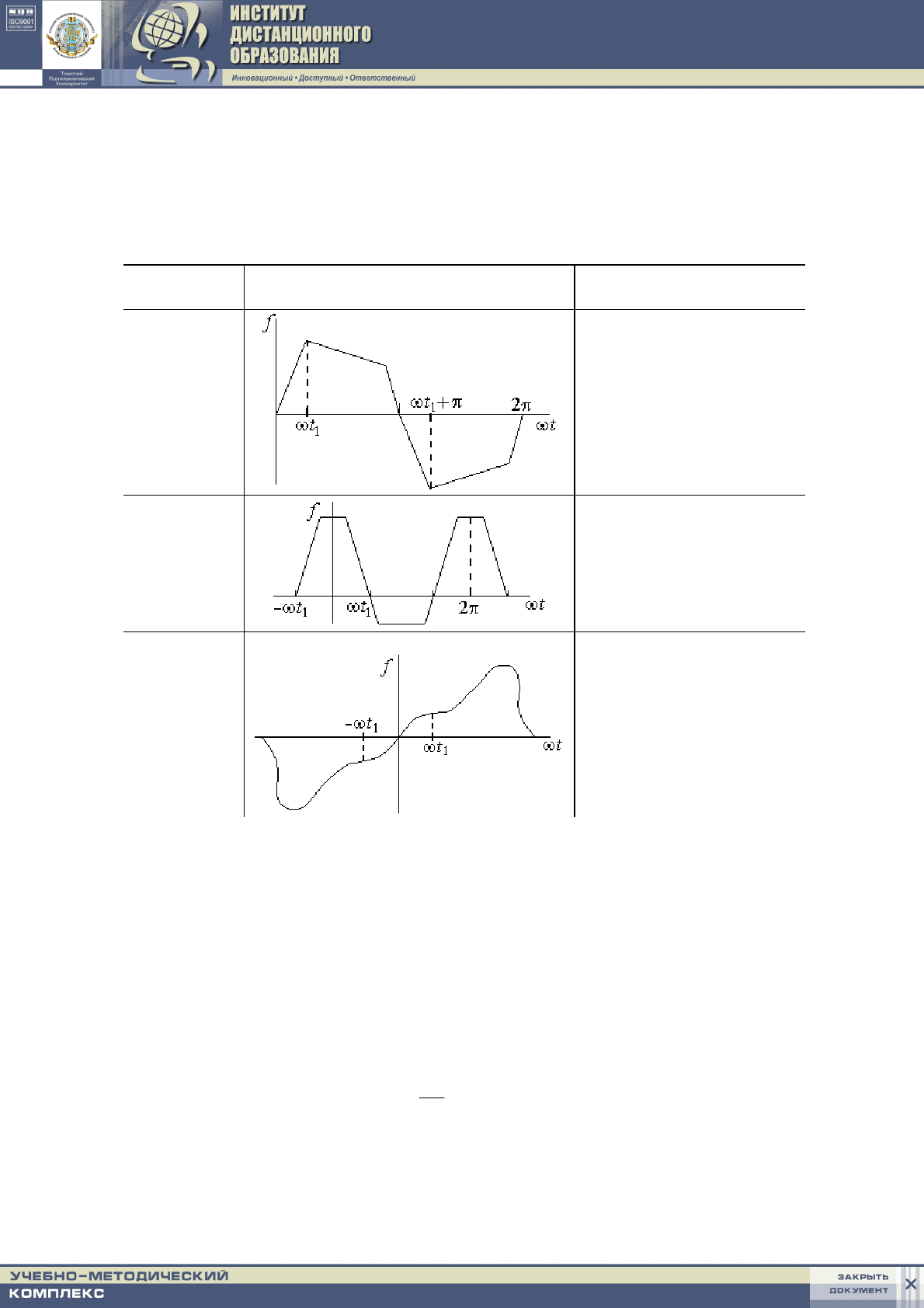
Теоретические основы электротехники. Ч. 1. Постоянный и синусоидаль-

ный токи в линейных цепях: учебное пособие / Р.Н. Сметанина, Г.В. Но-

сов, Ю.Н. Исаев. – 3-е изд., испр. – Томск: Изд-во ТПУ, 2009. – 118 с.

7.3. Частные случаи разложения в ряд Фурье

Значительное число несинусоидальных функций, с которыми при-

ходится встречаться в электротехнике, обладают различными видами

симметрии, поэтому их ряд Фурье не содержит тех или иных состав-

ляющих.

Вид

симметрии

График

f(ωt)

Ряд Фурье

(ωt)=f(ωt+π)

относительно

оси абсцисс

f(ωt) = А

sin(ωt

+ψ

)

sin(3ωt + ψ

) +

sin(5ωt + ψ

) +...

не содержит постоянной

составляющей и четных

гармоник

f(ωt) = f(–ωt)

относительно

оси ординат

f(ωt) = А

+ А

cosωt +

cos2ωt +

cos3ωt +...

не содержит синусных со-

ставляющих

f(ωt) = f(–ωt)

относительно

начала

координат

f(ωt) = А

sinωt +

sin2ωt +

sin3ωt +...

не содержит косинусных

составляющих и постоян-

ной составляющей

В приложении приведены примеры разложения периодических

функций (напряжений) в ряд Фурье.

7.4. Методы разложения периодических функций в ряд Фурье

7.4.1. Аналитический метод

Если несинусоидальная функция f (ωt) описана аналитически, то ко-

эффициенты ряда Фурье определяются как

()

;

∫

π−

ωω

= tdtfA

Теоретические основы электротехники. Ч. 1. Постоянный и синусоидаль-

ный токи в линейных цепях: учебное пособие / Р.Н. Сметанина, Г.В. Но-

сов, Ю.Н. Исаев. – 3-е изд., испр. – Томск: Изд-во ТПУ, 2009. – 118 с.

()

;sin

∫

π−

ωωω

= tdtktfB

()

.cos

∫

π−

ωωω

= tdtktfC

7.4.2. Приближенные методы разложения

Они основаны на приближенной замене интеграла конечной суммой.

Метод Перри

Период разбивается на четное число частей “n”, через точки деления

проводятся ординаты y

, и кривая заменяется ломаной, что позволяет

заменить интеграл суммой. Тогда коэффициенты определяются как

;

∑

;

sin

∑

mkm

cos

∑

mkm

По этому методу можно составить ряд не более чем из n/2 гармоник.

Существующее программное обеспечение ЭВМ позволяет быстро

произвести гармонический анализ любого периодического сигнала.

Кроме того, разложение в ряд Фурье некоторых простейших, но

наиболее часто встречающихся в электротехнике кривых приведены

в [1, Прил. 3].

7.5. Максимальные, средние и действующие значения

несинусоидальных функций

– это максимальное, т. е. наибольшее по модулю значение функ-

ции за период. F

ср

– это среднее значение функции за период, которое

равно F

– постоянной составляющей:

()

0ср

dttf

∫

Если кривая симметрична относительно оси абсцисс, то среднее по

модулю значение равно среднему значению за половину периода:

()

ср

∫

ω=

dttf

Теоретические основы электротехники. Ч. 1. Постоянный и синусоидаль-

ный токи в линейных цепях: учебное пособие / Р.Н. Сметанина, Г.В. Но-

сов, Ю.Н. Исаев. – 3-е изд., испр. – Томск: Изд-во ТПУ, 2009. – 118 с.

F – действующее значение – это среднеквадратическое значение функ-

ции за период:

()

[]

∑∑

∫

∞

+=+==

FFFFdttf

Действующее значение несинусоидальной функции равно корню

квадратному из суммы квадратов постоянной составляющей и дейст-

вующих значений всех гармоник.

Мгновенные значения Действующее значения

()

;sin

∑

∞

ψ+ω+=

kikm

tkIIi

u = U

+ ∑ U

sin(kωt + ψ

)

;

=+++=

IIII

=+++=

UUUU

Аналогично можно записать и для ЭДС.

7.6. Коэффициенты, характеризующие форму

несинусоидальных функций

При оценке несинусоидальных периодических кривых в электро-

энергетике, где кривые преимущественно симметричны относительно

оси абсцисс и не содержат постоянных составляющих, пользуются ко-

эффициентом формы кривой k

, коэффициентом амплитуды k

, коэффи-

циентом искажения k

, коэффициентом гармоник k

Коэффициент Определение

формы

ср

k =

отношение действующего значения к среднему по модулю

амплитуды

отношение максимального значения к действующему

искажения

отношение действующего значения первой гармоники

к действующему значению функции

гармоник

...

отношение действующего значения высших гармоник

к действующему значению первой гармоники