Сметанина Р.Н. и другие. Теоретические основы электротехники
Подождите немного. Документ загружается.

Теоретические основы электротехники. Ч. 1. Постоянный и синусоидаль-
ный токи в линейных цепях: учебное пособие / Р.Н. Сметанина, Г.В. Но-
сов, Ю.Н. Исаев. – 3-е изд., испр. – Томск: Изд-во ТПУ, 2009. – 118 с.
91
Между коэффициентами искажения и гармоник при отсутствии по-
стоянной составляющей существует следующая взаимосвязь:
2
и
и
Г
1
1
k
k
k −⋅= .
Сравнительная таблица коэффициентов
для постоянного и синусоидального тока
Коэффициент Постоянный ток Синусоидальный ток
k
ф
1
11,1
2
2
=
π
mm
FF
k
а
1
41,12
2
==
m
m
F
F
k
и
0 F
1
/ F = 1
k
Г
∞
0
7.7. Мощность в цепях с несинусоидальными источниками
Мгновенная
мощность p
p = ui = [U
0
+ ∑ U
km
sin(kωt + ψ
ku
)] [I
0
+ ∑ I
km
sin(kωt + ψ
ki
)];
P
0
= U
0
I
0
; p
k
= u
k
i
k
;
p ≠ P
0
+ ∑ p
k
;
для мгновенной мощности принцип наложения не применим
Активная
мощность Р
;cos
1
0
00
∑∑
∫
∞
=
=ϕ+==
k
kkkk
PIUIUdtui
T
P
;
0
∑
∞
=
=
k
k
PP
принцип наложения применим
Реактивная
мощность Q
∑∑
∞
=
∞
=
=ϕ=
11
sin
k
k
k
kkk
QIUQ
Полная
мощность S
;
2
2
2
1
2
0
2
2
2
1
2
0
IIIUUUUIS ++×++==
в общем случае S
2
≠ P
2
+ Q
2
Мощность
искажения T
()
;
222
QPST +−=
T – характеризует степень различия в форме кривых напря-
жения и тока
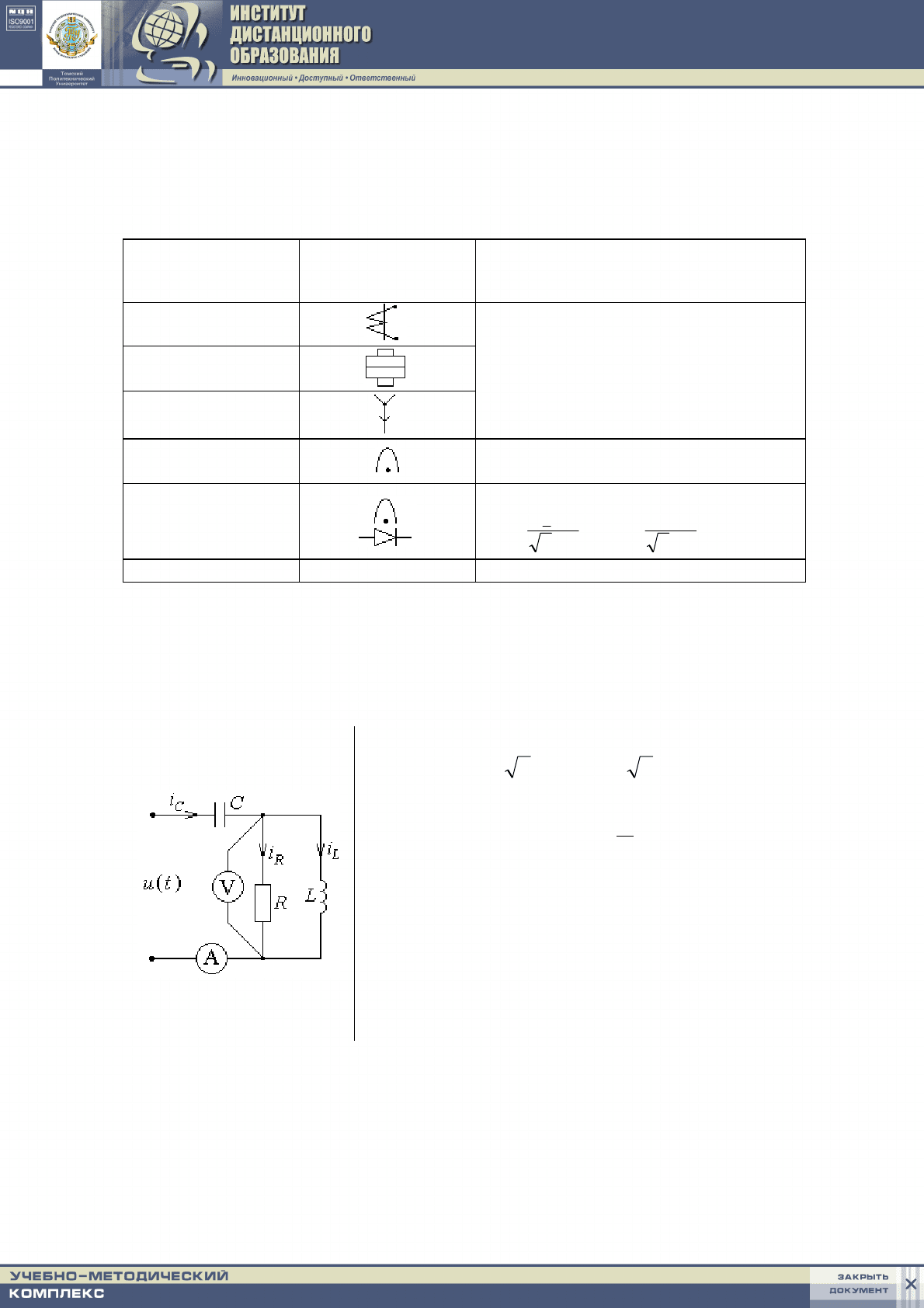
Теоретические основы электротехники. Ч. 1. Постоянный и синусоидаль-
ный токи в линейных цепях: учебное пособие / Р.Н. Сметанина, Г.В. Но-
сов, Ю.Н. Исаев. – 3-е изд., испр. – Томск: Изд-во ТПУ, 2009. – 118 с.
92
7.8. Особенности измерения несинусоидальных величин
В цепи с несинусоидальными источниками показания приборов,
включенных в цепь, зависят от типа прибора.
Тип
прибора
Условное
обозначение
Показание
электромагнитный
электро-
динамический
Действующее значение
несинусоидальной функции U, I
тепловой
магнито-
электрический
Постоянная составляющая U
0
; I
0
магнито-
электрический
с выпрямителем
Среднее по модулю значение
1,12
M
ср
⋅
=
m
I
I
;
1,12
M
ср
⋅
=
m
U
U
осциллограф Мгновенные значения u(t), i(t)
7.9. Расчет линейной цепи с несинусоидальными
источниками тока и ЭДС
Известно:
(
)
(
)
B903sin260sin27236
o
+ω+ω+= tttu ;
ω = 333,3 с
–1
; R = 30 Ом;
L = 0,03 Гн; С = 66,67 мкФ
_____________________________________
Рассчитать:
1. Мгновенные значения токов.
2. Действующие значения токов.
3. Активную мощность цепи (P).
4. Показания приборов:
а) электромагнитной системы;
б) магнитоэлектрической.
Теоретические основы электротехники. Ч. 1. Постоянный и синусоидаль-
ный токи в линейных цепях: учебное пособие / Р.Н. Сметанина, Г.В. Но-
сов, Ю.Н. Исаев. – 3-е изд., испр. – Томск: Изд-во ТПУ, 2009. – 118 с.
93
Порядок расчета Расчет цепи
1.
Представить заданные u(t)
или J(t) в ряд Фурье (ограни-
чиваясь “n” числом гармоник)
1.
u(t) = 36 + 72
,2 sinωt + 60 ,2 sin(3ωt + 90°) В;
Так как цепь линейная, то к расчету можно приме-
нять метод наложения, т. е. рассчитать цепь отдель-
но для каждой гармоники; n = 3
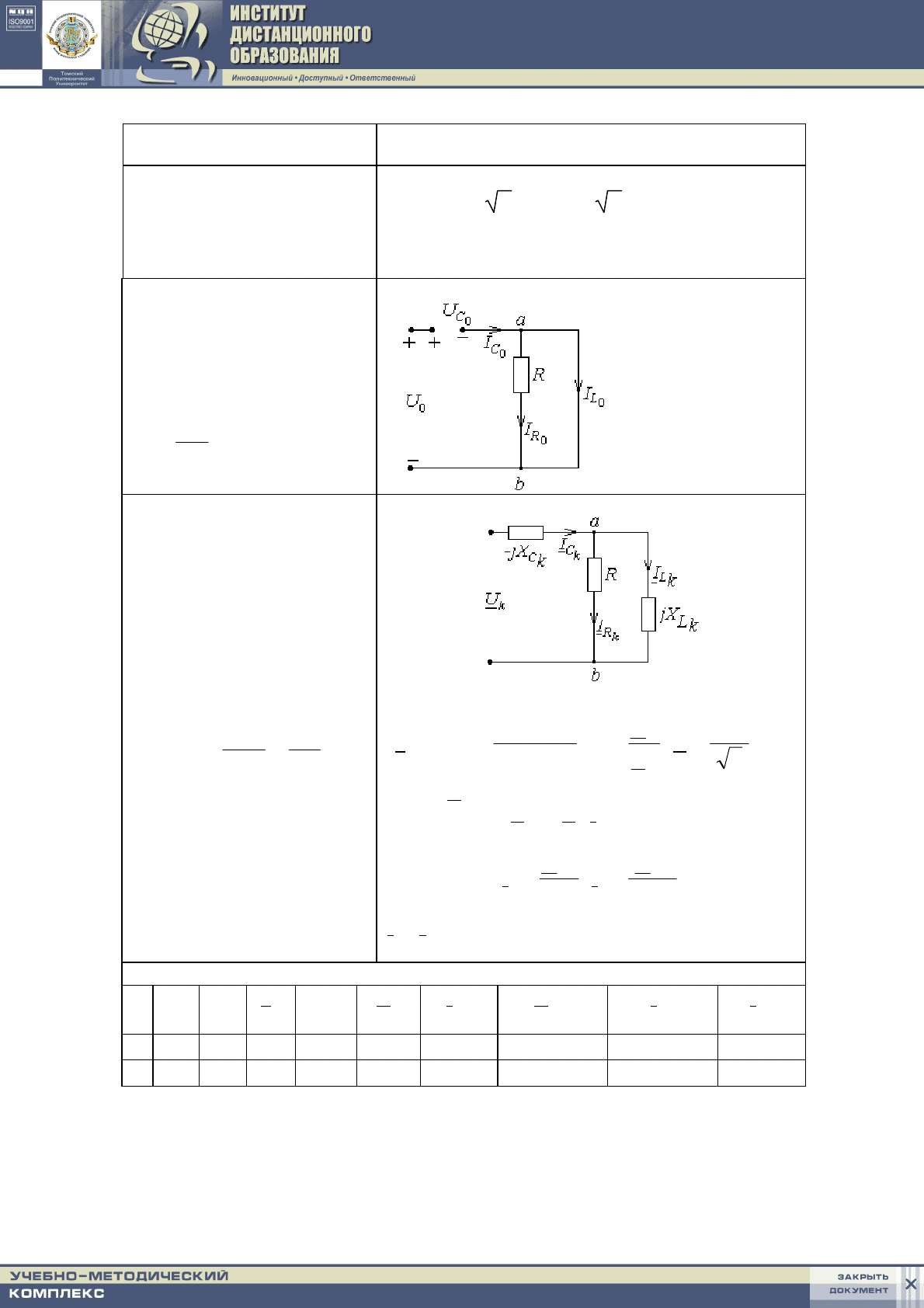
2.
Начертить схему замещения
для расчета постоянной со-
ставляющей с учетом того,
что ω = 0, X
L
0
= ωL = 0 (зако-
ротка);
X
C
0
=
Сω
1
= ∞ (разрыв)
2.
I
R
0
= I
C
0
= I
L
0
= 0;
U
C
0
= U
0
= 36;
U
ab
0
= 0
3.
Начертить комплексную схе-
му замещения для расчета
гармонических составляющих
и составить расчетные ком-
плексные уравнения любым
методом. Рассчитать сопро-
тивления (индуктивные и ем-
костные) для “k” гармоники:
X
L
k
= kωL = kX
L
1
;
X
C
k
=
k
x
Ck
C
1
1
=
ω
3.
Рассчитаем I
С
k
по закону Ома:
Z
k
= –jX
C
k
+
k
k
L
L
jXR
RjX
+
; I
С
k
=
k
k
Z
U
; U
k
=
2
km
U
е
jψ
k
.
Найдем U
ab
по второму закону Кирхгофа:
U
ab
k
= U
k
–I
C
k
(–jX
C
k
).
Найдем токи в ветвях по закону Ома:
I
R
k
=
R
U
ab
; I
L
k
=
k
L
ab
jX
U
(I
R
k
, I
L
k
можно найти по правилу токов параллель-
ных ветвей)
4. Результаты расчетов представим в виде таблицы
k
X
L
k
,
Ом
X
C
k
,
Ом
Z
k
,
Ом
ϕ
k
,
град
U
k
,
В
I
С
k
,
А
U
ab
k
,
В
I
R
k
,
А
I
L
k
,
А
1 10 45 36 –85,2 72
2 е
j85,2°
18,45 е
j156,8°
0,615 е
j156,8°
1,9 е
j66,8°
3 30 15 15 0
60 е
j90°
4 е
j90°
84,9 е
j135°
2,83 е
j135°
2,8 е
j45°
Теоретические основы электротехники. Ч. 1. Постоянный и синусоидаль-
ный токи в линейных цепях: учебное пособие / Р.Н. Сметанина, Г.В. Но-
сов, Ю.Н. Исаев. – 3-е изд., испр. – Томск: Изд-во ТПУ, 2009. – 118 с.
94
5.
Для контроля правильности
расчета составить баланс мощ-
ности для каждой гармоники,
справедливы также векторные
диаграммы
P
u
k
= P
п
k
,
U
k
I
k
cosϕ
k
=
∑
RI
k
2
5.
1) k = 0:
P
в
0
= U
0
I
0
= I
R
0
,
2
R = 0.
2) k = 1:
P
u
1
= U
1
I
С
1
cosϕ
1
= 72⋅2cos(–85,2°) = 11,3 Вт;
P
п
1
= (I
R1
)
2
R = 0,615
2
⋅30 = 11,35 Вт.
3) k = 3:
P
u
3
= 60⋅4cos(0°) = 240 Вт;
P
п
3
= 2,83
2
⋅30 = 240,2 Вт
6.
Записать мгновенные значения
токов ветвей, используя прин-
цип наложения
6.
i
C
= 2 2 sin(ωt + 85,2°) + 4 2 sin(3ωt + 90°) A;
i
R
= 0,615
2
sin(ωt + 156,8°) +
+ 2,83
2 sin(3ωt + 135°) A;
i
L
= 1,9 2 sin(ωt + 66,8°) +
+ 2,83
2 sin(3ωt + 45°) A
7.
Определить действующие зна-
чения токов ветвей и напряже-
ние U
ab
:
I =
∑
=
n
k
k
I
0
2
;
U =
∑
=
n
k
k
U
0
2
7.
I
C
=
22
42
+
= 4,47 А;
I
R
=
22
83,2615,0 + = 2,89 А;
I
L
=
22
83,29,1 + = 3,4 А;
U
ab
=
22
9,8445,18 +
= 86,88 B
8.
Рассчитать активную
мощность цепи:
Р
в
= Р
0
+
∑
=
n
k
k
Р
1
;
Р
п
=
∑
RI
2
8.
P
u
= P
u
0
+ P
u
1
+ P
u
2
= 11,3 + 240 = 251,3 Вт;
Р
п
= I
R
,
2
R = 2,89
2
⋅30 = 250,7 Вт.
Погрешность
δ =
п
п
P
PP
u
−
100 % = 0,29 %
9.
Определить показания
приборов
9.
I
A
= I
C
= 4,47 A;U
V
= U
ab
= 86,88 B;
I
A
= 0 A; U
V
= U
ab
= 0 B

Теоретические основы электротехники. Ч. 1. Постоянный и синусоидаль-
ный токи в линейных цепях: учебное пособие / Р.Н. Сметанина, Г.В. Но-
сов, Ю.Н. Исаев. – 3-е изд., испр. – Томск: Изд-во ТПУ, 2009. – 118 с.
95
Примечание. При наличии в цепи с несинусоидальными источниками
индуктивностей и емкостей может возникнуть резонанс для одной из
гармоник.
Условия резонанса прежние.
Резонанс напряжений Резонанс токов
X
эк
= 0;
0
1
=
ω
−ω
Ck
Lk
;
B
эк
= 0;
0
1
=ω−
ω
Ck
Lk
;
k
2
ω
2
LC = 1 .
В рассмотренном выше примере наблюдается резонанс напряжений
на третьей гармонике, когда ϕ
3
= 0.
Пример 1
Известно: R=4 Ом; 12
1
1
=
ω
=
C
X
C
Ом;
tttu ω+ω+= 2sin2,28sin2408)(
В;
цепь настроена на резонанс токов второй
гармоники.
Определить: а) полную мощность; б) ак-
тивную мощность; в) показания приборов
электродинамической системы.
Решение
1. Расчет постоянной составляющей (нулевой гармо-
ники):
2
4
8
0
0
===
R
U
I А; 0
0
=
V
U .
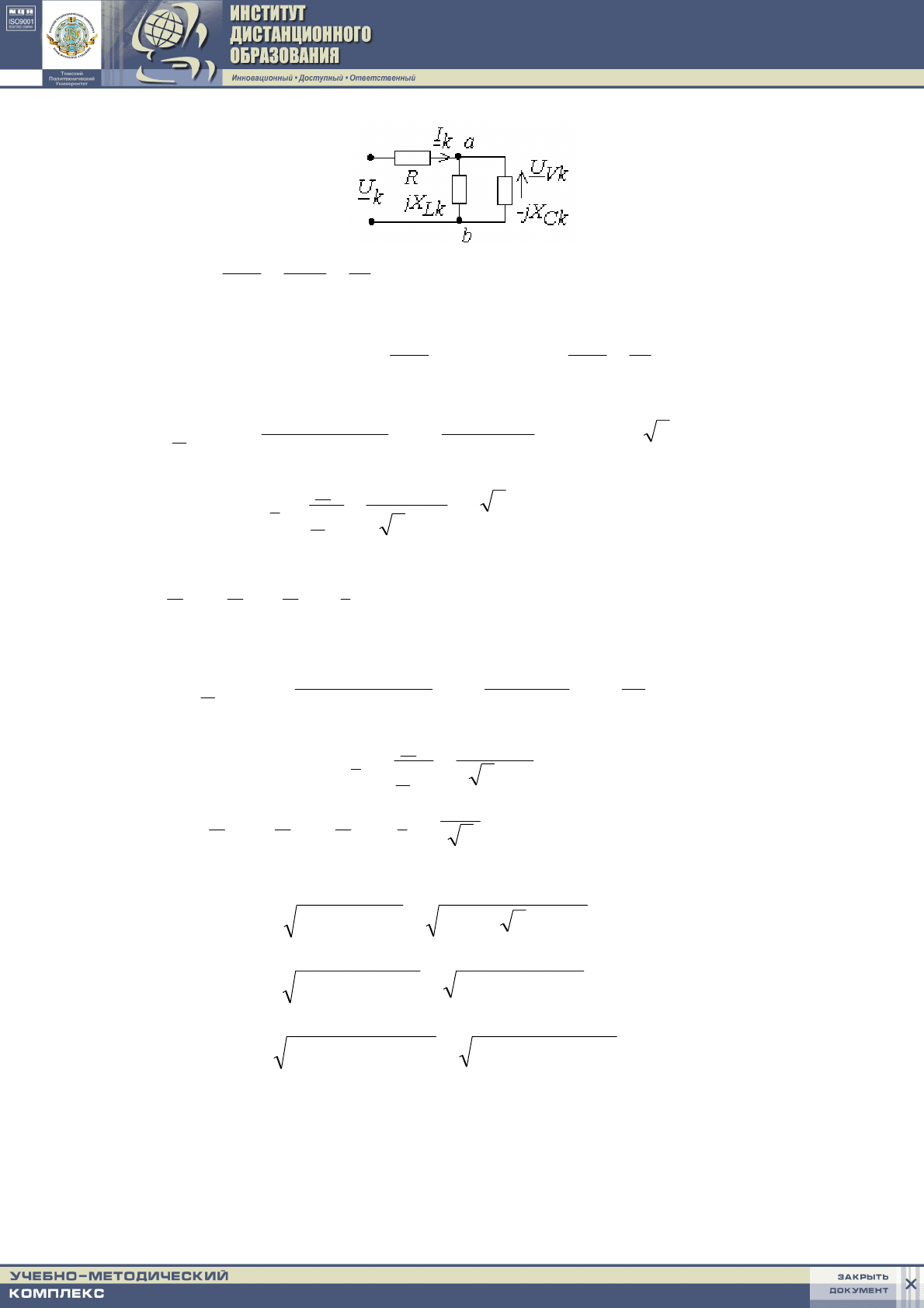
2. Изобразим комплексную схему для расчета гармо-
ник тока и напряжения:
Теоретические основы электротехники. Ч. 1. Постоянный и синусоидаль-
ный токи в линейных цепях: учебное пособие / Р.Н. Сметанина, Г.В. Но-
сов, Ю.Н. Исаев. – 3-е изд., испр. – Томск: Изд-во ТПУ, 2009. – 118 с.
96
где
kCkk
X
X
C
Ck
121
1
=
ω
== Ом;
LkkXX
LLk
ω
=
=
1
Ом, причем при резо-
нансе токов второй гармоники имеем
2
2
1
212
C
CLL
X
XXX
===
, тогда
3
4
12
4
1
1
===
C
L
X
X
Ом.
3. Рассчитаем первые гармоники (k=1):
Ом;2444
123
)12(3
4
)(
45
11
11
1
o
j
CL
CL
Э
ej
jj
jj
jXjX
jXjX
RZ =+=
−
−
⋅
+=
−
−⋅
+=
5525
24
40
45
45
0
1
1
1
je
e
e
Z
U
I
j
j
j
Э
−====
−
o
o
o
А.
Напряжение на участке ab найдем по второму закону Кирхгофа:
oo
450
1
111
2,282020)55(440
jj
Vab
ejjeIRUUU =+=−⋅−=−== В.
4. Рассчитываем вторые гармоники (k=2) при резонансе токов:
6
22
=
=
CL
XX Ом;
∞=+=
−
−
⋅
+=
−
−⋅
+=
0
36
4
66
)6(6
4
)(
22
22
2
jj
jj
jXjX
jXjX
RZ
CL
CL
Э
Ом;
0
2
2,28
0
2
2
2
=
∞⋅
==
o
j
Э
e
Z
U
I
;
oo
00
2
222
202004
2
2,28
jj
Vab
eeIRUUU ==⋅−=−== В.
5. Рассчитываем действующие значения:
а) входного тока
33,70)25(2
2222
2
2
1
2
0
=++=++= IIII А;
б) входного напряжения
43,4520408
2222
2
2
1
2
0
=++=++= UUUU В;
в) напряжения на вольтметре
6,34202,280
2222
2
2
1
2
0
=++=++=
VVVV
UUUU В.
6. Рассчитываем:
а) полную мощность цепи
33433,743,45
=
⋅
=
⋅=
I
U
S
ВА;
Теоретические основы электротехники. Ч. 1. Постоянный и синусоидаль-
ный токи в линейных цепях: учебное пособие / Р.Н. Сметанина, Г.В. Но-
сов, Ю.Н. Исаев. – 3-е изд., испр. – Томск: Изд-во ТПУ, 2009. – 118 с.
97
б) активную потребляемую в цепи мощность
215433,7
22
=⋅== RIP Вт.
7. Запишем показания приборов электродинамической системы, ко-
торые измеряют действующие значения периодических напряжений и
токов:
а) показание амперметра
IA=I=7,33 A;
б) показание вольтметра
UV=34,6 В.
Ответ:
S = 334 ВА; P = 215 Вт;
IA=7,33 A ; UV = 34,6 В.
Пример 2
Известно: R=30 Ом; L
1
=0,15 Гн; L
2
=0,1 Гн;
ttte 200sin60100sin29060)( ++= В;
в параллельной ветви резонанс напряжений
на первой гармонике.
Рассчитать:
а) действующие значения токов всех вет-
вей;
б) показания приборов магнитоэлектри-
ческой и электромагнитной систем.
Решение
1. Расчет постоянной составляющей (ну-
левой гармоники):
1
302
60
2
0
2010
=
⋅
===
R
E
II
А; 0
30
=I ;
30130
100
=
⋅
=
⋅
=
IRU
V
В.
2. Изобразим схему для расчета напря-
жения и токов, где
1111 LkL
kXLkX
=
ω
=
;
2122 LkL
kXLkX
=
ω
=
;
k
X
Ck
X
C
Ck
1
1
=
ω
= ;
1515,0100
111
=
⋅
=
ω
=
LX
L
Ом;
101,0100
221
=
⋅
=
ω
=
LX
L
Ом;
причем при резонансе напряжений первой гармоники имеем
10
211
==
LC
XX
Ом.
3. Рассчитываем первые гармоники (
k=1) при резонансе напряжений
в параллельной ветви:

Теоретические основы электротехники. Ч. 1. Постоянный и синусоидаль-
ный токи в линейных цепях: учебное пособие / Р.Н. Сметанина, Г.В. Но-
сов, Ю.Н. Исаев. – 3-е изд., испр. – Томск: Изд-во ТПУ, 2009. – 118 с.
98
=
−+
−
⋅
++=
)(
)(
121
121
11
1
CL
CL
L
Э
jXjXR
jXjXR
jXRZ
o
6,26
54,331530
)1010(30
)1010(30
1530
j
ej
jj
jj
j
=+=
−+
−⋅
++=
Ом;
o
o
o
6,26
6,26
0
1
1
11
7,2
54,33
90
j
j
j
Э
e
e
e
Z
E
I
−
=== А;
0
)1010(30
1010
7,2
)(
6,26
121
121
1121
=
−+
−
⋅=
−+
−
⋅=
−
jj
jj
e
jXjXR
jXjX
II
j
CL
CL
o
;
oo
6,266,26
121
1131
7,2
)1010(30
30
7,2
)(
jj
CL
e
jj
e
jXjXR
R
II
−−
=
−+
⋅=
−+
⋅= А;
=+⋅=+⋅=
−
)1530(7,2)(
6,26
11
11
1
jejXRIU
j
LV
o
ooo
06,266,26
6,9054,337,2
jjj
eee =⋅=
−
В.
4. Рассчитываем вторые гармоники (k=2):
=
−+
−
⋅
++=
)5,02(
)5,02(
2
121
121
11
2
CL
CL
L
Э
XjXjR
XjXjR
XjRZ
o
4,49
3,554236
)520(30
)520(30
3030
j
ej
jj
jj
j =+=
−+
−⋅
++=
Ом;
o
o
o
4,49
4,49
0
2
2
12
77,0
3,552
60
j
j
j
Э
e
e
e
Z
E
I
−
=
⋅
== А;
A;34,0
)520(30
520
77,0
)5,02(
5,02
144,49
121
121
1222
oo
jj
CL
CL
e
jj
jj
e
XjXjR
XjXj
II
=
−+
−
⋅=
=
−+
−
⋅=
−
;A7,0
)520(30
30
77,0
)5,02(
764,49
121
1232
oo
jj
CL
e
jj
e
XjXjR
R
II
−−
=
−+
⋅=
=
−+
⋅=
oo
4,44,49
11
12
2
6,32)3030(77,0)2(
jj
L
V
ejeXjRIU
−−
=+⋅=+⋅= В.
5. Рассчитываем действующие значения:
98,277,07,21
2222
12
2
11
2
101
=++=++= IIII А;
06,134,001
2222
22
2
21
2
202
=++=++= IIII А;
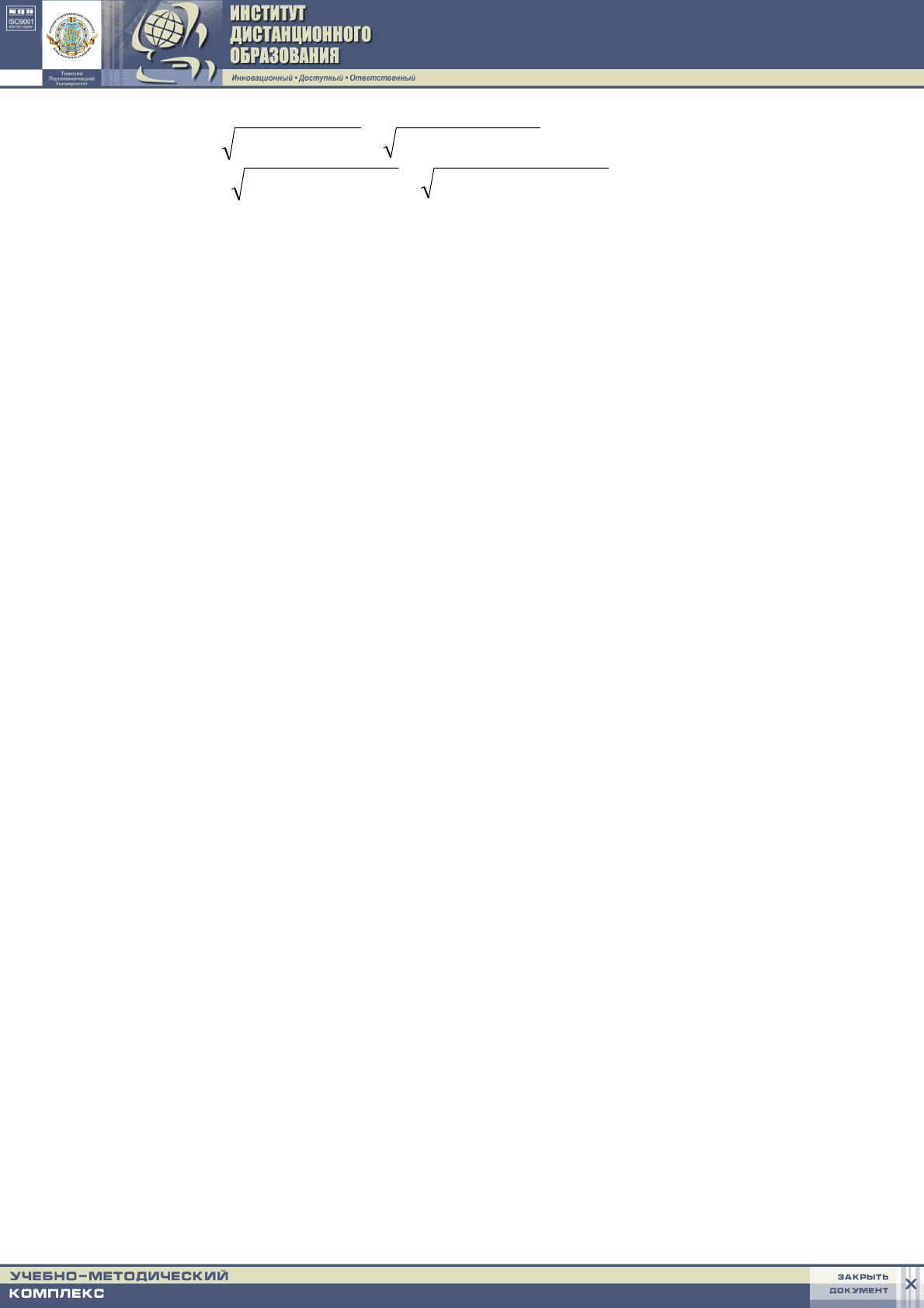
Теоретические основы электротехники. Ч. 1. Постоянный и синусоидаль-
ный токи в линейных цепях: учебное пособие / Р.Н. Сметанина, Г.В. Но-
сов, Ю.Н. Исаев. – 3-е изд., испр. – Томск: Изд-во ТПУ, 2009. – 118 с.
99
79,27,07,20
2222
32
2
31
2
303
=++=++= IIII
А;
9,1006,326,9030
2222
2
2
1
2
0
=++=++=
VVVV
UUUU В.
6. Определяем показания приборов:
а) магнитоэлектрической системы, которые измеряют постоянные
составляющие
U
V
= U
V0
= 30 B;
I
A
= I
20
= 1 A.
б) электромагнитной системы, которые измеряют действующие зна-
чения
U
V
= 100,9 B;
I
A
= I
2
= 1,06 A.
Теоретические основы электротехники. Ч. 1. Постоянный и синусоидаль-
ный токи в линейных цепях: учебное пособие / Р.Н. Сметанина, Г.В. Но-
сов, Ю.Н. Исаев. – 3-е изд., испр. – Томск: Изд-во ТПУ, 2009. – 118 с.
100
Тема 8
ЧЕТЫРЕХПОЛЮСНИКИ
В различных областях электротехники особенно часто применяются
устройства с двумя парами выводов, при помощи которых они соеди-
няются с другими участками электрической цепи, – это четырехполюс-
ники.
Четырехполюсник – электрическая схема, имеющая два входных и
два выходных зажима.
⎩
⎨
⎧
−
−
′
−
величины;входные
1
1
зажимы;первичные11
I,U
⎩
⎨
⎧
−
−
′
−
величины.выходные
2
2
зажимы;вторичные22
I,U
8.1. Классификация четырехполюсников
8.1.1. По схемам соединения
Г-образная Т-образная
П-образная Мостовая
