Сметанина Р.Н. и другие. Теоретические основы электротехники
Подождите немного. Документ загружается.


41
Топографическая диаграмма
– из конца одного вектора напряжения
следует другой. Диаграмма напряжений строится для контура на осно-
вании II закона Кирхгофа относительно векторов токов с учетом харак-
тера элементов (§ 2.5). Расположение векторов соответствует располо-
жению элементов в схеме.
Активный Индуктивный Емкостной
При построении диаграммы напряжений потенциал одной точки
принимается за ноль и эта точка помещается в начало координат. По
диаграмме напряжений можно определить напряжение между любыми
точками схемы, соединив эти точки и поставив стрелку.
Например:
Первая буква в обозначении указывает на точку высшего потенциа-
ла, т. е. точку, куда направлен вектор напряжения.
Пример построения диаграммы
Схема электрической цепи
Комплексная схема замещения
42
Уравнения по законам Кирхгофа
в комплексной форме
:
1.
I
1
=
I
2
+
I
3
.
2.
U
L
1
+
U
R
2
+
U
C
2
+
U
C
1
=
E
.
3.
U
R
2
+
U
C
2
–
U
R
3
= 0.
Векторная диаграмма токов
и напряжений
Пример
Комплексная схема замещения
Рассчитать цепь, комплексная схема
замещения представлена на рисунке.
Дано:
E=
75
o
6,15j
e
−
= (72,24 –
j
20,17) B;
J
=
o
60
1
j
e
−
= (0,5 –
j
0,866) A;
Z
1
= –
j
22,7 Ом;
Z
2
= (14,4 –
j
25) Ом;
Z
3
= 28,8 Ом;
Z
4
=
j
33,3 Ом;
Z
5
= (14,4 –
j
25) Ом;
Рассчитать:
I
1
,
I
2
,
I
3
,
I
4
,
I
5
,
U
J
.
Составить баланс мощностей; построить векторные диаграммы токов
и напряжений.
Решение
Так как в схеме к
1
= 4 – 1 = 3, к
2
= 6 – 4+1 = 3, но в третьем контуре
находится источник тока, то контурный ток этого контура равен току
источника, тогда количество неизвестных контурных токов равно двум,
поэтому выбираем метод контурных токов. Направим контурные токи
против часовой стрелки, и составим систему трех уравнений
I
33
=
J
( )
⎪
⎩
⎪
⎨
⎧
+−=−−−
=+++−
+=−++
)3(.)(
)2(,)(
)1(,
3353223115
33322432114
33522411541
IZZuIZIZ
IZIZZZIZ
IZEIZIZZZ
J

Теоретические основы электротехники. Ч. 1. Постоянный и синусоидаль-
ный токи в линейных цепях: учебное пособие / Р.Н. Сметанина, Г.В. Но-
сов, Ю.Н. Исаев. – 3-е изд., испр. – Томск: Изд-во ТПУ, 2009. – 118 с.
43
Решая полученную систему с помощью определителей или с помощью
стандартной программы ЭВМ, получим
I
11
=2 A;
I
22
=1
o
60j
e
=0,5+
j
0,866 A;
U
J
= – 43,19 –
j
24,83 = 49,82
o
150j
e
−
B.
Примечание
. Можно сначала совместно решить
(
1
)
и
(
2
)
урав-
нение, т.к. в них не входит U
J
, а затем из
(
3
)
рассчитать U
J
.
Теперь по контурным токам рассчитаем токи ветвей:
I
1
=
I
11
= 2 A;
I
2
=
I
22
=
o
60
1
j
e
A;
I
3
=
I
22
–
I
33
=
j
1,73=
o
90
73,1
j
e
A;
I
4
=
I
11
–
I
22
= 1,73
o
30j
e
−
A;
I
5
=
I
11
–
I
33
= 1,73
o
30j
e
A.
Составим баланс мощностей.
Комплексная мощность источников
S
u
=
*
1
*
JUIE
J
⋅+
= (72,24 –
j
20,17)
⋅
2 +
+ (–43,19 –
j
24,83)(0,5 +
j
0,866) = (144,3 –
j
90,5) BA;
P
u
= 144,3 Вт;
Q
u
= –90,5 вар.
Мощность потребителей
R
k
= Re
Z
k
;
X
Lk
=
Im
Z
k
;
P
п
=
1444,1473,18,2873,14,141
222
2
2
53
2
32
2
2
=⋅+⋅+⋅=++ RIRIRI
Вт;
Q
п
=
()( ) ( )
=−++−+−
5
2
54
2
42
2
21
2
1
XIXIXIXI
=
()() ( )
2,902573,13,3373,12517,222
2222
−=−+⋅+−+−
ВАр.
Погрешность вычислений
100
п
⋅
−
=δ
u
u
P
P
PP
%
100
3,144
1443,144
⋅
−
=
%
= 0,2
%
< 1
%
;
100
п
⋅
−
=δ
u
u
Q
Q
QQ
%
100
5,90
2,905,90
⋅
−
=
%
= 0,33
%
< 1
%
.
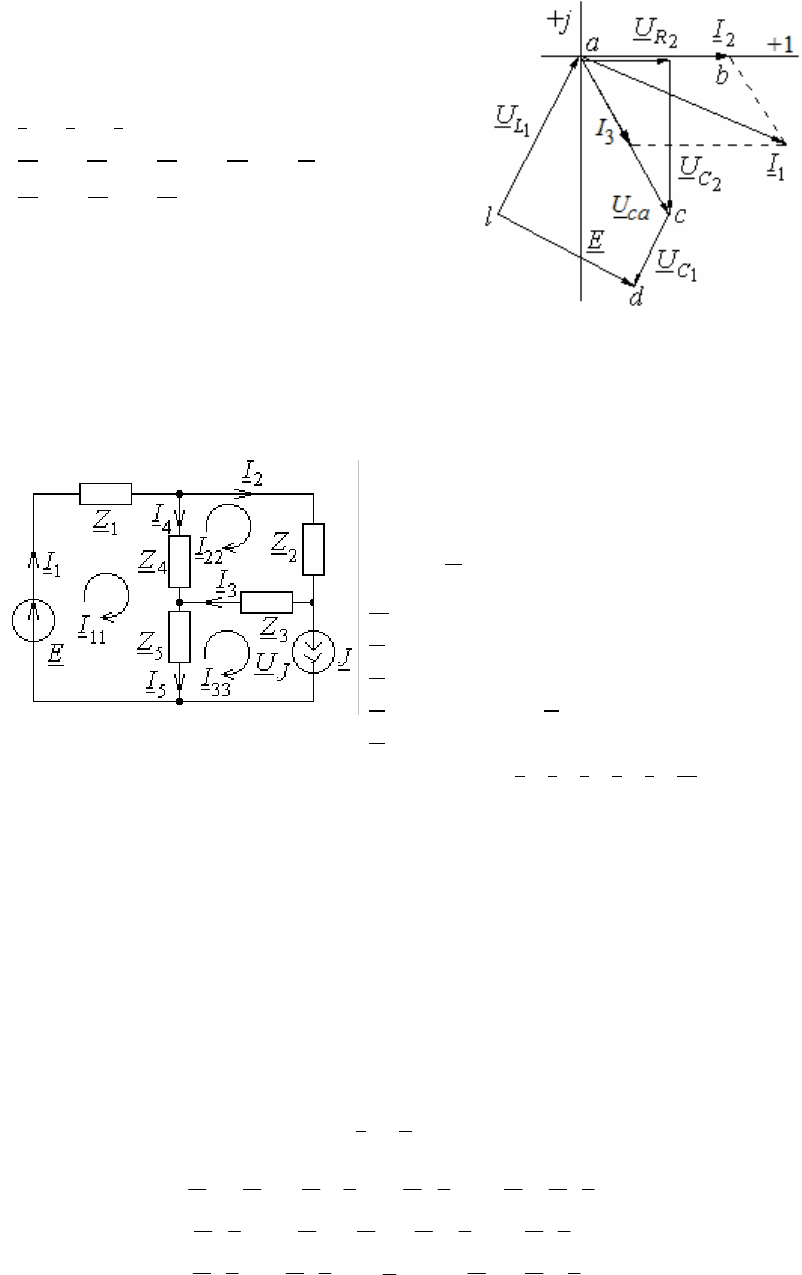
Построим лучевую диаграмму токов и топографическую диаграмму
напряжений. Для этого изобразим комплексную схему замещения,
представив заданные сопротивления
Z
в виде активных и реактивных
элементов. Вычислим падения напряжения на каждом элементе в ком-
плексной форме.
Масштаб:

Теоретические основы электротехники. Ч. 1. Постоянный и синусоидаль-
ный токи в линейных цепях: учебное пособие / Р.Н. Сметанина, Г.В. Но-
сов, Ю.Н. Исаев. – 3-е изд., испр. – Томск: Изд-во ТПУ, 2009. – 118 с.
44
;A2
1
=I
A1
60
2
o
j
eI =
;
;, A731
3
jI =
A731
30
4
o
j
eI
−
=
,
;
A731
30
5
o
j
eI ,=
;
o
150
82,49
j
J
eU
−
=
B;
B75
615
o
,
j
eE
−
=
; A1
60
o
j
eJ
−
=
;
m
I
= 0,5 А/см;
m
U
= 10 В/см.
()( )
B;4,457,222
1
1
1
jjjXIU
X
−=−=−=
B;4,144,141
6060
2
2
2
oo
jj
R
eeRIU =⋅==
() ()
B;25251
3060
2
2
2
oo
jj
X
ejejXIU
−
=−=−=
B;82,498,2873,1
3
3
3
jjRIU
R
=⋅==
B;6,573,3373,1
6030
4
4
4
oo
jj
X
ejejXIU =⋅==
−
B;91,244,1473,1
3030
5
5
5
oo
jj
R
eeRIU =⋅==
() ()
B25,432573,1
6030
5
5
5
oo
jj
X
ejejXIU
−
=−=−=
.
Сначала строим лучевую диаграмму токов по комплексным значе-
ниям токов, по которой можно проверить выполнение I закона Кирхго-
фа для каждого узла.
Для построения топографической диаграммы напряжений примем
ϕ
d
= 0 и поместим точку d в начало координат. От точки d строим векто-

45
ры напряжений в той последовательности, как они нарисованы на схеме,
ориентируя их относительно своих токов согласно характеру элемента
(см. § 3.7) и проверяя соответствие углов напряжений относительно по-
ложительной действительной оси.
По топографической диаграмме напряжений проверяем выполнение
второго закона Кирхгофа для каждого контура, следовательно, убежда-
емся в правильности расчетов.
Тема 4
РЕЗОНАНСНЫЕ ЯВЛЕНИЯ
И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
Резонансом
называют такой режим пассивной цепи, содержащей L и
С, при котором входное реактивное сопротивление или входная реак-
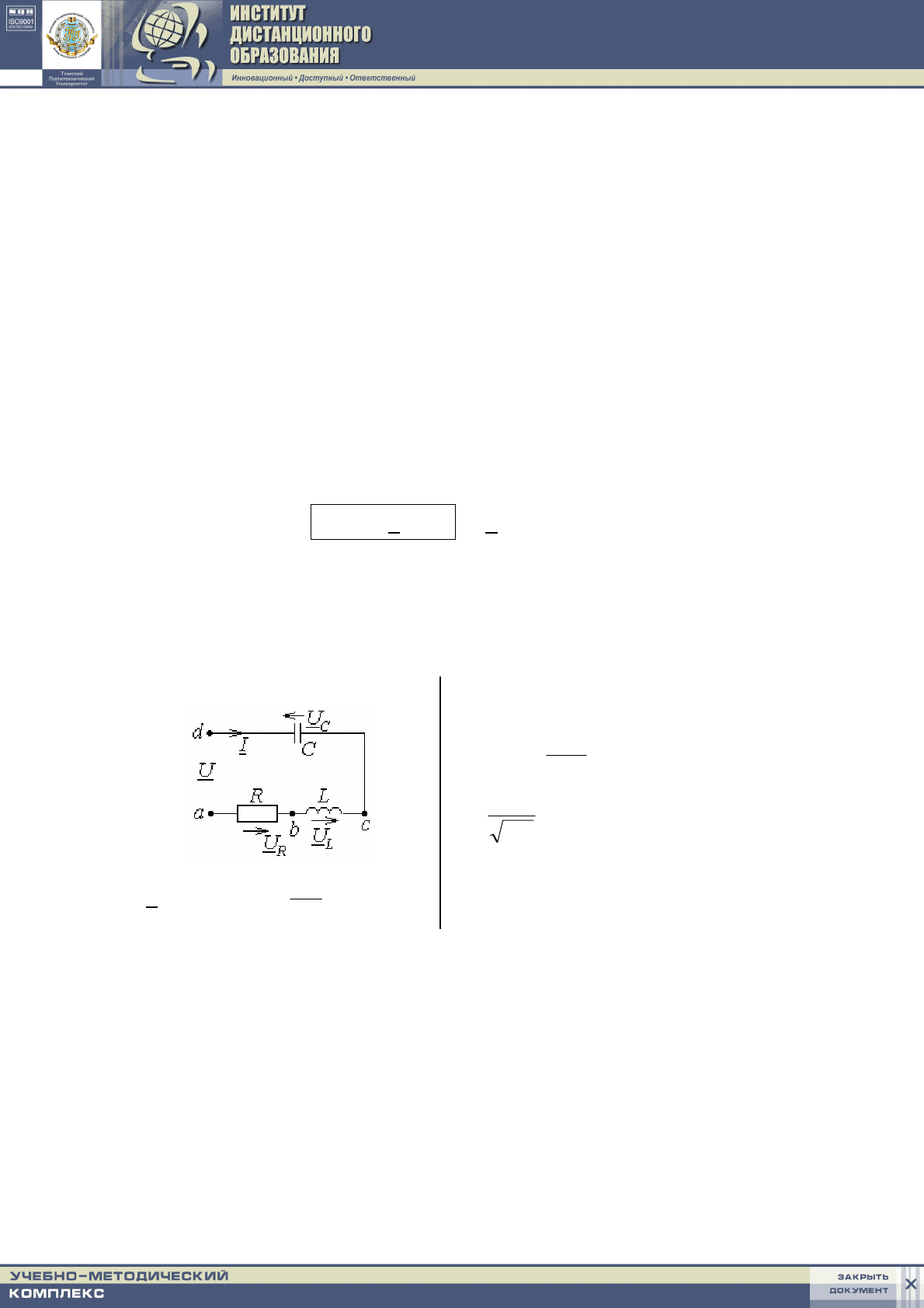
Теоретические основы электротехники. Ч. 1. Постоянный и синусоидаль-
ный токи в линейных цепях: учебное пособие / Р.Н. Сметанина, Г.В. Но-
сов, Ю.Н. Исаев. – 3-е изд., испр. – Томск: Изд-во ТПУ, 2009. – 118 с.
46
тивная проводимость равны нулю, при этом входной ток и напряжение
совпадают по фазе.
Различают
резонанс напряжений и резонанс токов.
4.1. Резонанс напряжений
1. Условие резонанса напряжений в сложной цепи.
Резонанс напряжений наблюдается в электрической цепи с последо-
вательным соединением участков, содержащих индуктивности и емко-
сти. При резонансе напряжений индуктивное сопротивление одной час-
ти цепи компенсируется емкостным сопротивлением другой части цепи,
последовательно соединенной с первой. В результате реактивное сопро-
тивление и реактивная мощность на зажимах цепи равны нулю.
Тогда можно записать условие резонанса напряжений в сложной це-
пи:
X = Jm(Z
) = 0. Z = R + jX.
2. Резонанс в последовательном контуре R, L, C.
Неразветвленная цепь, состоящая из последовательно соединенных
элементов R, L, C, представляет один из простейших случаев резонанс-
ной цепи.
Схема
Z = R + j
⎟
⎠
⎞
⎜
⎝
⎛
−
C
L
ω
1
ω = R + jX
Условие резонанса:
X = ω
0
L –
C
0
ω
1
= 0;
ω
0
=
LC
1
– резонансная угловая
частота
Теоретические основы электротехники. Ч. 1. Постоянный и синусоидаль-
ный токи в линейных цепях: учебное пособие / Р.Н. Сметанина, Г.В. Но-
сов, Ю.Н. Исаев. – 3-е изд., испр. – Томск: Изд-во ТПУ, 2009. – 118 с.
47
Основные соотношения
при резонансе:
Z
min
= R; I
max
=
R
U
;
ϕ = arctg
R
X
= 0;
U
L
= jω
0
L I ; U
C
= –j
C
0
ω
1
I
;
L
U =
C
U (по модулю);
U =
R
U , P=UI (Вт), Q=0 (вар).
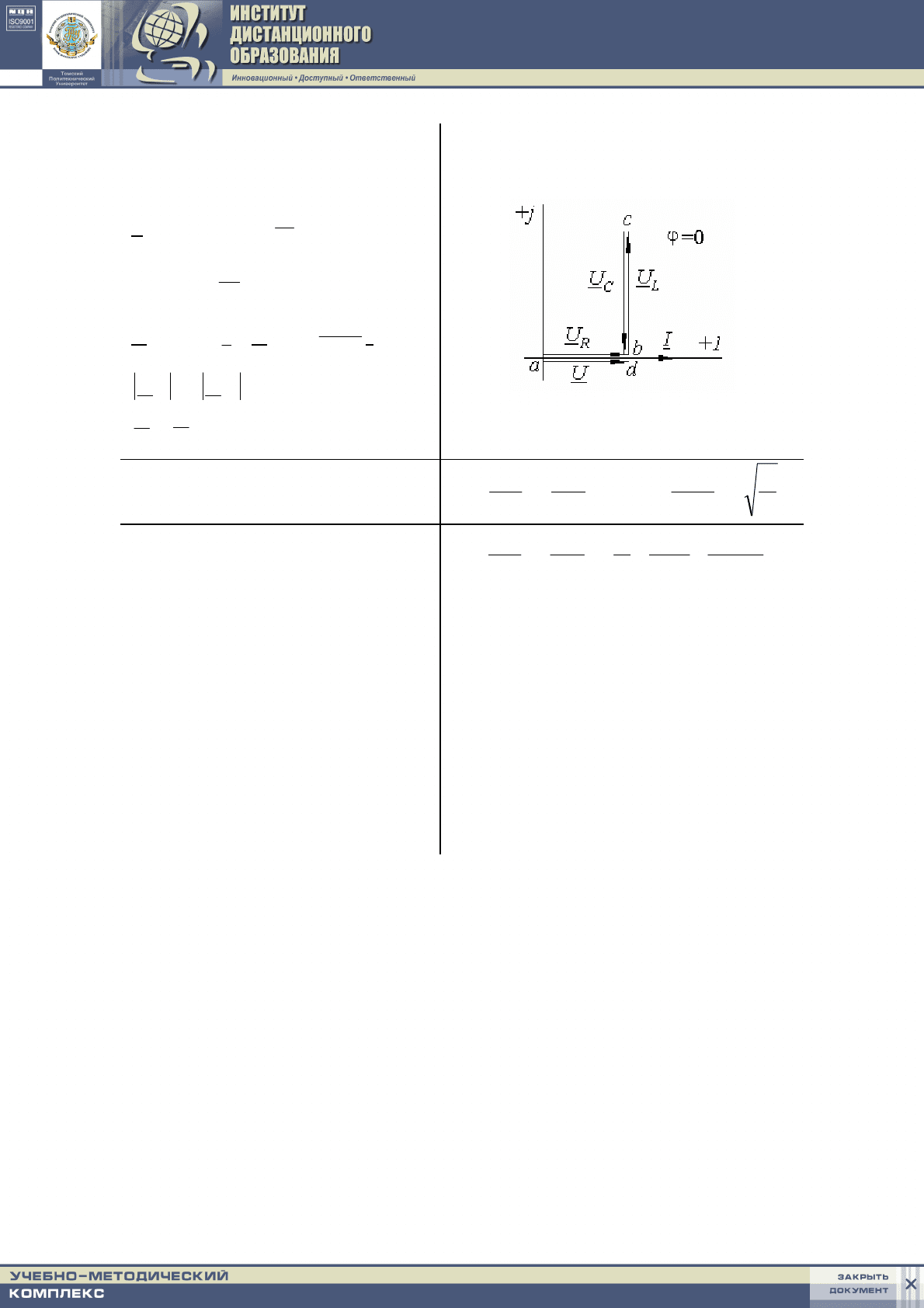
Векторная диаграмма
Характеристическое сопро-
тивление контура
ρ =
I
U
L
=
I
U
C
= ω
0
L =
C
0
ω
1
=
C
L
Так как в режиме резонанс
а
напряжений ток достигает мак-
симального значения, то напря-
жение на индуктивности и емко-
сти при резонансе может значи-
тельно превышать напряжение н
а
входных клеммах цепи.
Добротность контура q пока-
зывает, во сколько раз напряже-
ние на каждом из реактивных
элементов превосходит входное
напряжение в режиме резонанса.
q =
U
U
L
=
U
U
C
=
R
ρ
=
R
L
0
ω
=
CR
0
ω
1
;
q >> 1 , если ρ >> R.
4.2. Частотные и резонансные характеристики
Если к последовательному резонансному контуру приложено сину-
соидальное напряжение u = U
m
sinωt, амплитуда которого неизменна,
а частота может изменяться в пределах от 0 до ∞, – это приведет к изме-
нению его реактивного и полного сопротивления, угла ϕ.
Зависимости от частоты параметров цепи называют частотными
характеристиками, зависимости действующих или амплитудных зна-
чений тока и напряжения от частоты – резонансными кривыми.

Теоретические основы электротехники. Ч. 1. Постоянный и синусоидаль-
ный токи в линейных цепях: учебное пособие / Р.Н. Сметанина, Г.В. Но-
сов, Ю.Н. Исаев. – 3-е изд., испр. – Томск: Изд-во ТПУ, 2009. – 118 с.
48
Зависимости реактивных
сопротивлений от частоты:
X
L
= ωL;
X
C
=
С
ω
1
;
X = X
L
–X
C
.
Зависимость тока
от частоты (АЧХ):
I =
2
2
ω
1
ω
⎟
⎠
⎞
⎜
⎝
⎛
−+
C
LR
U
;
при ω = ω
0
I
m
=
R
U
π
ω
−
ω
2
12
= П
f
– полоса пропускания
Зависимость фазы
от частоты (ФЧХ):
ϕ = arctg
R
X
; X = ωL –
C
ω
1
при ω = ω
0
ϕ = 0
Зависимость U
L
и U
С
от частоты:
U
L
= ωLI; U
C
=
C
ω
1
I
ω
C
< ω
0
< ω
L
; при ω = ω
0
U
L
= U
С
Теоретические основы электротехники. Ч. 1. Постоянный и синусоидаль-
ный токи в линейных цепях: учебное пособие / Р.Н. Сметанина, Г.В. Но-
сов, Ю.Н. Исаев. – 3-е изд., испр. – Томск: Изд-во ТПУ, 2009. – 118 с.
49
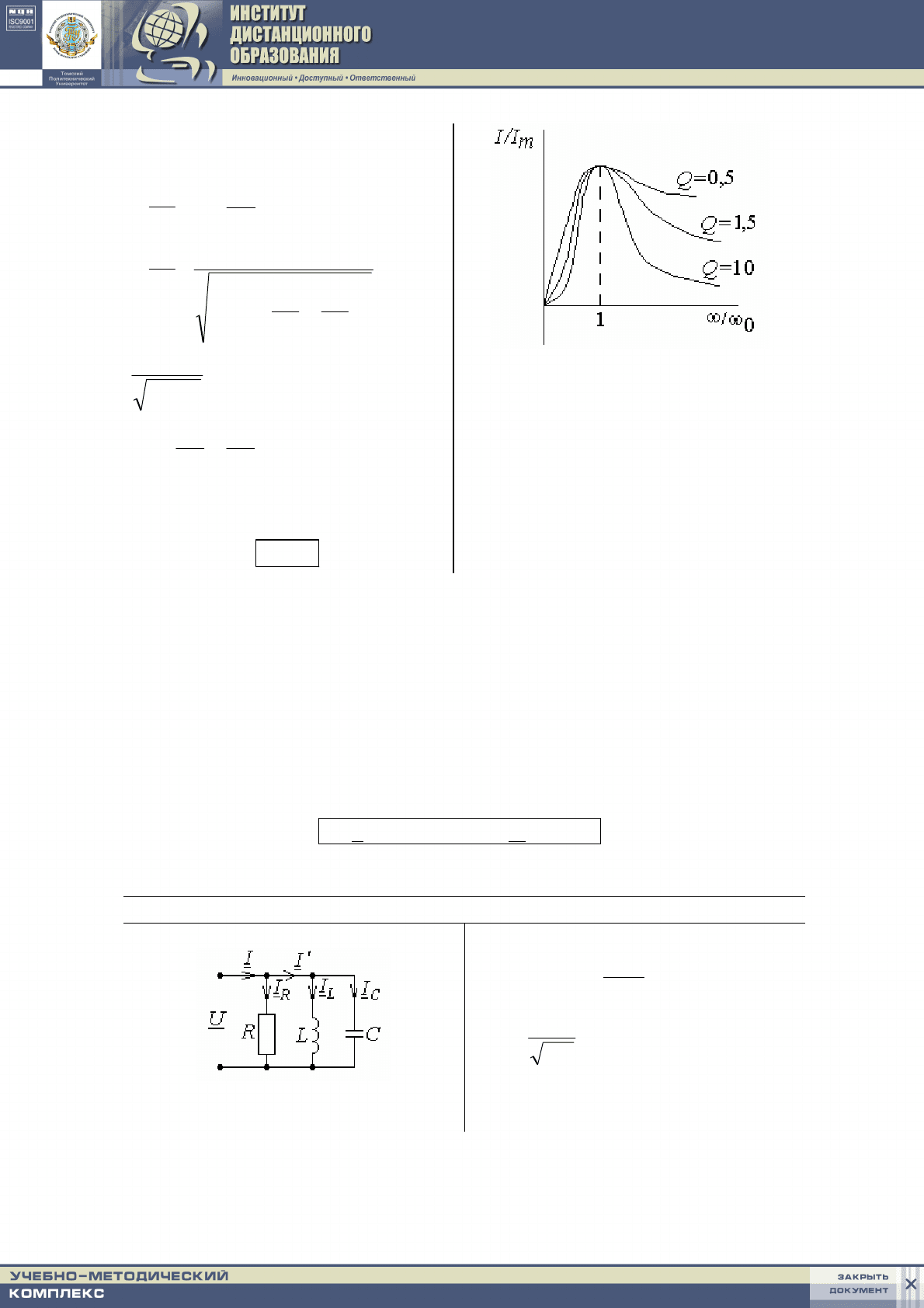
Влияние добротности контура
на ход резонансной кривой:
m
I
I
= f
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
ω
ω
0
;
m
I
I
=
2
0
0
2
q1
1
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
ω
ω
−
ω
ω
+
=
2
1
1
ξ+
;
q
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
ω
ω
−
ω
ω
0
0
= ξ;
ξ – обобщенная расстройка кон-
тура, при резонансе
ξ = 0
чем больше
q, тем уже полоса
пропускания контура
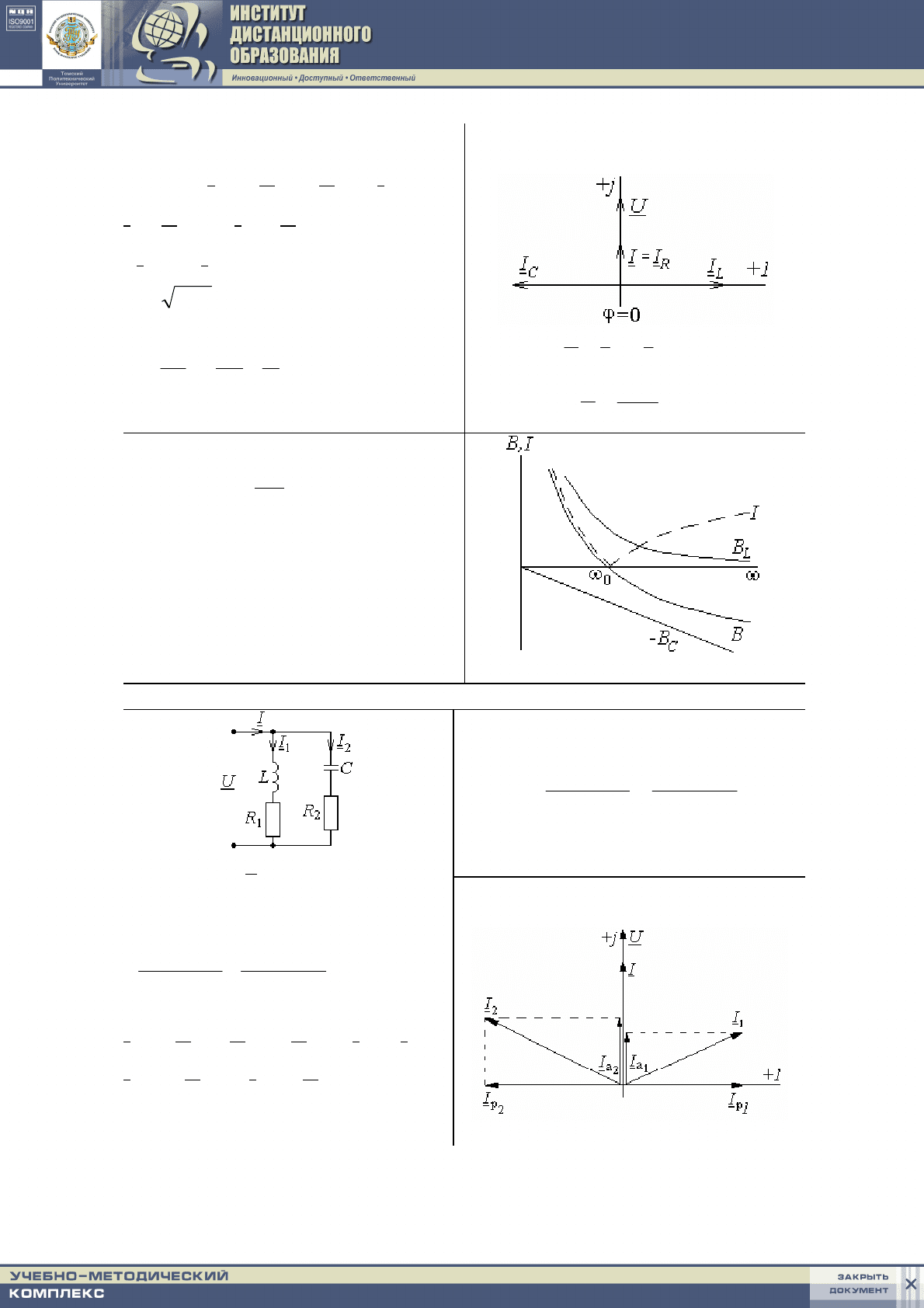
4.3. Резонанс токов в параллельном контуре R, L, C
Резонанс токов наблюдается в электрической цепи с параллельным
соединением участков, содержащих индуктивности и емкости.
При резонансе токов индуктивная проводимость одной части цепи
компенсируется емкостной проводимостью другой части цепи, парал-
лельно соединенной с первой. В результате реактивная проводимость и
реактивная мощность на зажимах цепи равны нулю.
Условие резонанса токов:
Jm(Y) = 0, B = 0, где Y = G – jB.
Резонансный контур без потерь
Y = G – j(B
L
– B
C
) = G – jB
Условие резонанса:
B = B
L
– B
C
=
L
0
1
ω
– ω
0
C = 0;
ω
0
=
LC
1
– резонансная частота
Теоретические основы электротехники. Ч. 1. Постоянный и синусоидаль-
ный токи в линейных цепях: учебное пособие / Р.Н. Сметанина, Г.В. Но-
сов, Ю.Н. Исаев. – 3-е изд., испр. – Томск: Изд-во ТПУ, 2009. – 118 с.
50
Основные соотношения:
Y
min
= G; I
min
= U⋅G = U/R = I
R
;
I
L
= U/jω
0
L; I
C
= jUω
0
C;
⏐
I
L
⏐ = ⏐I
C
⏐ (по модулю);
ρ =
L/C – характеристическое
сопротивление;
q =
I
I
L
=
I
I
C
=
R
ρ
– добротность
контура
Векторная диаграмма
0=
+
=
′
CL
III ,
или
0=
⋅
=
′
BUI
Частотные характеристики:
B
L
=
L
ω
1
;
B
C
= ωC;
B = B
L
– B
C
; I = UY
Резонансный контур с потерями
Y = G –jB
Условие резонанса:
B = 0;
B =
22
1
L
L
XR
X
+
–
22
2
C
C
XR
X
+
=
=
B
L
–B
C
= 0
Основные соотношения:
Y
min
= G = G
1
+ G
2
=
=
22
1
1
L
XR
R
+
+
22
2
2
C
XR
R
+
;
I
min
= UG = UG
1
+ UG
2
= Ia
1
+ Ia
2
;
I
р
1
= –jUB
L
; I
р
2
= jUB
C
;
I
р
2
= I
р
1
(по модулю).
Векторная диаграмма
