Шинкарик М.І. Вища математика

Подождите немного. Документ загружается.

331

кутника -

iii

x)(fs Δ⋅

, а площа східчастої фігури даного розбит-

тя

∑

Δ⋅ξ=

iin

x)(fS

, де )(f

значення функції f в точці

, а

.xxx

1iii −

−=Δ

Якщо ж тепер кількість точок розбиття збільшувати,

одночасно зменшуючи

1iii

xxx

−

−=Δ , то площу S трапеції можна

записати, як

∑

=Δ

Δξ=

0xmax

x)(flimS

Доведено, що вибір точок розбиття на площу

S не впливає.

◙ Задача про об'єм виробництва із змінною продуктивністю

праці

Аналізуючи будь-яке виробництво видно, що продуктивність

є величина змінна і в різні моменти різна. Нехай продуктивність за

період від

0 до t (певний період часу) описується функцією f(t).

Розіб'ємо проміжок [

0;t] на n проміжків тривалістю

tΔ і вважаючи

продуктивність за час

tΔ сталою і рівною )t(f

визначимо, приб-

лизно, об’єм продукції виробленої за проміжок часу

; t

) як

∑

Δ=

t)t(f)l,k(K

. Тоді, збільшуючи кількість проміжків роз-

биття, одержуємо все точніші формули для обчислення об’єму ви-

робленої продукції. Якщо ж

∞→

→Δ

то

∑

Δ=

∞→

t)t(flimK

2.2. Визначений інтеграл, як границя інтегральних сум

Проведемо міркування аналогічно до міркувань попереднього

пункту. Для неперервної функції

f(x) визначеної на

[]

b,a

, і для роз-

биття (

bx...xxхa

n210

=<<<<= ) (мал.2.) запишемо суму

.x)(fx)(f...x)(fx)(fx)(f

iinn332211

∑

Δξ=Δξ++Δξ+Δξ+Δξ

(6.27)

Суму (6.27) називають інтегральною сумою. Введемо ще одну

величину maxΔx

- це довжина найбільшого з відрізків Δx

-x

i-1

Означення 3. Функція f(x) називається інтегровною на

[]

b,a ,

якщо існує скінчена границя

∑

→Δ

Δξ

0xmax

,x)(flim

яка не залежить

332

від того, яким чином проміжок

[]

b,a поділений на часткові

проміжки і яким чином вибираються точки

на цих часткових

проміжках, тільки б довжина максимального з них прямувала до

нуля. ( 0xmax

→Δ ).

Означення 4. Число I називається границею інтегральної суми

∑

Δξ

x)(f , якщо для будь-якого довільного 0>ε знайдеться таке

,0>δ

що як тільки δ<Δ

xmax , то виконується нерівність

ε<−Δξ

∑

Ix)(f ,незалежно від вибору часткових проміжків

n321

x...x,x,x ΔΔΔΔ

і точок

на цих проміжках.

Означення 5. Визначеним інтегралом від функції f(x) на

проміжку

[]

b,a

називається границя

∑

→Δ

Δξ

0xmax

.x)(flim

Позначається

∑

∫

→Δ

Δξ=

0xmax

.x)(flimdx)x(f

Числа a i b називаються, відповідно, нижньою і верхнею межами

інтегрування, а

[]

b,a

– проміжок інтегрування.

На основі цих означень можна записати, що

∫

dx)x(fS - формула для знаходження площі фігури (мал. 2.) і

∫

dt)t(fK - формула для знаходженння об’єму виробництва. (6.2.1)

Для границь інтегральних сум зберігаються багато властивостей

границь послідовностей або функцій. Проте, з означення визначеного

інтеграла не випливає, що будь-яка функція є інтегровна на будь-якому

інтервалі. Є такі функції для яких не існує визначений інтеграл .

Відповідь на питання про існування визначеного інтеграла дає така

теорема:

ТЕОРЕМА 9. Якщо функція f(x) неперервна на замкненому

проміжку

[]

b,a

, то вона інтегровна на цьому проміжку, тобто для

неї існує визначений інтеграл

.dx)x(f

∫

Теорема доводиться в ширших курсах вищої математики.

333

ТЕОРЕМА 10. Якщо, на

[]

b,a

функція обмежена і має лише

скінчене число точок розривів, то вона інтегровна на

[]

b,a

Ця

теорема дає можливість інтегрувати розривні функції.

Інтеграл

∫

dx)x(f

був означений для випадку .ba <

Доповнимо означення. Якщо ba > , то

∫∫

−=

dx)x(fdx)x(f

(6.28)

а якщо ,ba = то .0dx)x(f

∫

= (6.29)

2.3. Основні властивості визначеного інтеграла

З означення

∑

∫

→Δ

Δξ=

0xmax

x)(flimdx)x(f

одержуємо:

Властивість

.0dx)x(f

∫

(6.30)

Властивість

.dx)x(fdx)x(f

∫∫

−=

(6.31)

Доведемо ще декілька інших властивостей.

ТЕОРЕМА 11. (Властивість

3) Нехай c – проміжна точка

проміжку

[]

b,a

(

)bca <<

. Тоді виконується рівність

,dx)x(fdx)x(fdx)x(f

∫∫∫

якщо всі три інтеграли

,dx)x(f

∫∫

dx)x(f

∫

dx)x(f

існують.

Доведення. За умовою bca << і всі три інтеграли, про які

йде мова, існують. Розіб’ємо проміжок

[]

b,a

на n часткових

проміжків:

[][ ][ ][ ]

b,x...x,x,x,x,x,a

1n32211 −

з довжинами, відповідно

,,...,

ΔΔ

так щоб точка с була точкою поділу. (Наприклад

)).nm(cx

Тоді інтегральна сума

)x)(f(

∑

Δξ

, що

відповідає проміжку

[]

b,a

розіб’ється на два доданки:

.x)(fx)(fx)(f

∑∑∑

===

Δξ+Δξ=Δξ

334

Перейшовши до границі при

0xmax

→Δ

одержимо

.dx)x(fdx)x(fdx)x(f

∫∫∫

(6.32)

ТЕОРЕМА 12. ( Властивість

4) Сталий множник можна

виносити за знак визначеного інтеграла.

.dx)x(fkdx)x(kf

∫∫

(k=const) (6.33)

Доведення. За означенням

∫

dx)x(kf

[]

=Δα+++Δα+Δα=

→Δ

in2211

0xmax

x)(kf...x)(kfx)(kflim

∑

→Δ

Δα=

0xmax

x)(kflim

На основі властивості границь, про те, що константу можна виноси-

ти за знак границі та означення інтеграла, одержуємо:

.dx)x(fkx)(flimkdx)x(kf

0xmax

∑

∫∫

→Δ

=Δα=

ТЕОРЕМА 13. (Властивість

5) Визначений інтеграл від

алгебраїчної суми декількох неперервних функцій дорівнює

алгебраїчній сумі визначених інтегралів від цих функцій.

Доведення. В загальному випадку все можна звести до

розгляду такого виразу

[]

.dx)x(f)x(f)x(f

321

∫

−+

(6.34)

За означенням інтеграла, і врахувавши властивість границь (пункт

3.4.1.), одержуємо

[][ ]

=Δξ−ξ+ξ=−+

∑

∫

→Δ

332211

0xmax

321

x)(f)(f)(flimdx)x(f)x(f)x(f

.dx)x(fdx)x(fdx)x(f

x)(flimx)(flimx)(flim

ii3

0xmax

0xmaz

0xmax

1ii

∫∫∫

∑∑∑

−+=

=Δξ−Δξ+Δξ=

→Δ

335

2.4. Теорема про середнє значення визначеного інтеграла.

ТЕОРЕМА 14.

( про середнє значення визначеного інтеграла).

Якщо функція f(x) неперервна на проміжку

[]

b,a , то

всередині нього знайдеться така точка

с, що

∫

−=

)c(f)ab(dx)x(f

. (6.35)

Доведення. Якщо функція

f(x) неперервна на проміжку

[]

b,a

то вона досягає своїх найбільшого і найменшого значення

М і m на

проміжку

[]

b,a

. (пункт 3.6.2.) Розіб’ємо проміжок

[]

b,a

на n част-

кових проміжків довжиною

).n,...,3,2,1i(xxx

1iii

=−=Δ

−

Оскільки

m)(f

≥

для будь-якого

з проміжку

[]

і1і

х,х

−

, то

.xmx)(f

iii

Δ≥Δ

Врахувавши,що

.abx...xxx

n21

−=Δ++Δ+Δ=Δ

∑

Одержимо

)ab(mx)(f

−≥Δξ

∑

(6.36)

Аналогічно,

,M)(f

≤

а тому )ab(Mx)(f

−≤Δξ

∑

(6.37)

Об’єднавши ці дві нерівності (6.36) і (6.37), одержимо

∑

−≤Δξ≤−

)ab(Mx)(f)ab(m

Якщо

0xmax

→Δ

то

∫

−≤≤−

)ab(Mdx)x(f)ab(m .

або

dx)x(f

≤

−

≤

∫

(b>a)

Врахуємо теорему про те, що функція

f(x), неперервна на

проміжку

[]

b,a

набуває на ньому всі проміжні значення між своїм

найбільшим і найменшим значеннями, відповідно

. Нехай в

точці

с : M)c(fm ≤≤ де )bса( ≤≤ .

336

Тоді )c(f

dx)x(f

−

∫

, значить ).c(f)ab(dx)x(f

−=

∫

(6.38)

А це й треба було довести.

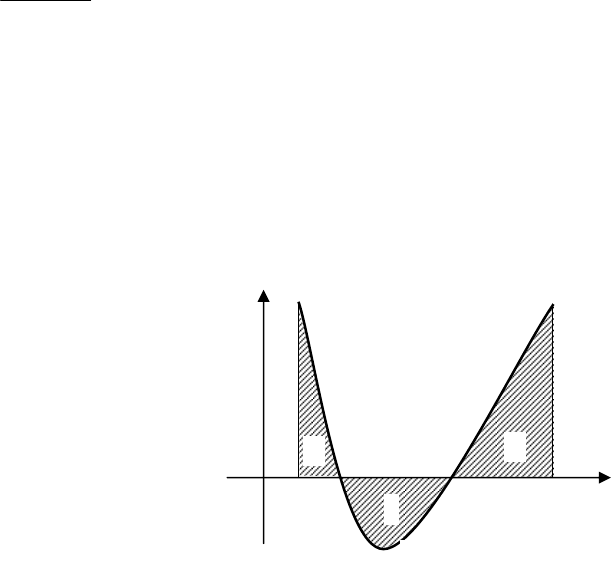
2.5. Геометричний зміст визначеного інтеграла.

Раніше ми вияснили, що площа криволінійної трапеції, яка

обмежена зверху кривою

),x(fy =

знизу – проміжком

[]

b,a

осі Ох

(

)bxa ≤≤ і з бічних сторін – прямими

ах =

вх =

, дорівнює:

.x)(flimS

0xmax

∑

→Δ

Δξ=

Це значить, що

.dx)x(fS

∫

Якщо ж функція на

(а;b)

змінює знак. На

(а;с) і (d;b)

– додатна, а на (c;d) –

від'ємна, то і відповідні

значення інтегралів будуть

додатними і від'ємним.

(мал.3). Тому площу

криволінійної трапеції,

зображеної на малюнку ,

обчислюють за формулою:

∫∫∫

−+=++=

dx)x(fdx)x(fdx)x(fCED.плDbB.плaAC.плS .

Це потрібно враховувати при знаходженні площ за допомогою ви-

значеного інтеграла і при обчисленні визначеного інтеграла. В ви-

падку, якщо

)x(fy = - непарна функція то,

0dx)x(f

∫

−

, якщо ж

– парна, то

∫∫

−

dx)x(f2dx)x(f

Мал.3

337

2.6. Зв'язок невизначеного і визначеного інтегралів.

Формула Ньютона-Лейбніца.

Одним з важливих моментів цього розділу є знаходження

зв’язку між визначеним і невизначеним інтегралами.

Невизначений інтеграл

∫

dx)x(f

- це функція, а визначений інте-

грал

∫

dx)x(f

- число. Який між ними зв’язок? Якщо величину b –

замінити змінною

і розглянути )х(Фdt)t(f

∫

, як функцію ,

то для цього інтеграла виконується теорема, про властивість визна

ченого інтеграла із змінною верхньою межею.

ТЕОРЕМА

15. Якщо функція )x(f неперервна на

[]

b,a ,

то похідна визначеного інтеграла

∫

dt)t(f з змінною верхньою

межею

х по цій межі дорівнює значенню підінтегральної

функції при

= , тобто

).x(f'dt)t(f

∫

)(

(6.39)

Доведення. Розглянмо

функцію

dt)t(f)х(Ф

∫

= ,

де f(t) –неперервна на [a,b]

функція. Доведемо, що Ф(х) має

похідну

()

).x(fхФ =

′

Задамо

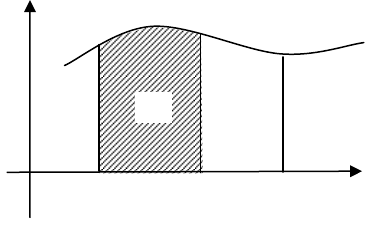
змінній х приріст Δх. Тоді Ф(х)

буде мати приріст

)х(Ф)хх(ФФ −Δ+=Δ ,

який на малюнку 4 зображається

площею криволінійної трапеції

СВВ

. Але

∫

Δ+

=Δ+

dt)t(f)хх(Ф

()

∫

=Φ

dt)t(fх .

Тому

∫∫

−=ΔΦ

Δ+ x

dt)t(fdt)t(f .

Мал. 4

х+

y=f(x)

ΔФ

338

На основі теореми (11) одержимо

()

∫∫∫

Δ+Δ+

хх

dt)t(fdt)t(fdttf

Значить

∫

Δ+

=ΔΦ

dt)t(f

. Застосовуючи теорему (14), знаходимо

),c(fx)c(fx)xx(dt)t(f

⋅Δ=⋅−Δ+==ΔΦ

∫

Δ+

][

де

< c < x+ xΔ . Звідси випливає що )c(f

ΔΦ

. (6.40)

Спрямуємо

хΔ до нуля. Тоді )хх( Δ+ буде прямувати до х, а зна-

чить і

с прямуватиме до х. Внаслідок неперервності f(x), одержимо

)x(f)c(flim)c(flim

xc0x

→→Δ

Переходячи до границі в рівності (6.40), одержимо

)x(f)c(flim

lim

0x0x

ΔΦ

→Δ→Δ

. Тобто ).x(f)x(Ф =

′

Але

,dt)t(f)х(Ф

∫

= а тому ).x(f

dt)t(fd

dФ

∫

][

Проте, базовою при обчисленні визначеного інтеграла, є на-

ступна теорема.

ТЕОРЕМА

16. (Ньютона-Лейбніца). Визначений інтеграл

від неперервної функції

)x(f

дорівнює різниці значень її перві-

сної

)x(F при

bx =

і ,

де

-нижня і верхня межі інте-

грування, тобто має місце формула

∫

−=

)a(F)b(Fdt)х(f . (6.41)

Доведення. Розглянемо функцію

∫

.dt)t(f)x(Ф

За теоремою 15 функція

Ф(х) є первісною для )x(f на проміжку

[]

b,a

. Значить .C)x(Fdt)t(f

∫

+= Але дві первісних для

однієї й тієї ж функції відрізняються лише на константу.

339

Тобто Ф(х) =

C)x(F +

Якщо ж

= , одержимо

C)a(Fdt)t(f

∫

Оскільки

0dt)t(f

∫

та

,C)a(F0 +=

то

,C)a(F −=

).a(FC −=

А отже

∫

−=

).a(F)x(Fdt)t(f

При

bx =

одержимо

∫

−=

)a(F)b(Fdt)t(f .

Ця формула називається формулою Ньютона-Лейбніца і дає

найпростіший метод для знаходження визначеного інтеграла.

Її прийнято записувати так:

).a(F)b(F

)x(F

dx)x(f

−==

∫

2.7. Методи обчислення визначеного інтеграла

В більшості випадків обчислення визначеного інтеграла зво-

диться до знаходження первісної для відповідного невизначеного

інтеграла, а потім використовується формула Ньютона-Лейбніца.

Тому всі методи, які використовуються для знаходження невизначе-

ного інтеграла використовуються для знаходження визначеного

інтеграла.

◙ Заміна змінної в визначеному інтегралі

Нехай дано

∫

dx)x(f ,

)x(f

- неперервна на [a;b]. Заміна

змінної для визначеного інтеграла полягає в тому, що вводиться но-

ва змінна, зв’язана з попередньою співвідношенням

)t(x

= така,

що

)t(

- неперервно диференційована на [a;b]. Якщо при зміні t

від

α до β, х змінюється від a до b, )(a α

= , )(b

= і складна

функція

))t((f

визначена і неперервна на відрізку [α;β],

то правильна формула

∫∫

′

ϕ= dt)t())t((fdx)x(f

. (6.42)

340

Приклад 22. Обчислити

∫

−

dxx4 .

Розв

’язування. Вводимо нову змінну за формулою tsin2x = . Ви-

значимо нові межі інтегрування. Якщо

х = 0, то 0tsin2 = і t = 0 –

нижня межа інтегрування. Якщо

х = 2, то 2tsin2 = і

= - верхня

межа інтегрування. Отже

t буде змінюватись від 0 до

. Тоді

==−=−

∫∫∫

ππ

tdtcos4tdtcos2tsin44dxx4

π=+=+=

∫

)

t2sin

t(2dt)t2cos1(2

◙ Метод інтегрування за частинами

Полягає в застосуванні формули:

[]

.vduuvudv

∫∫

−= (6.43)

Приклад 23. Обчислити

.dxxe

∫

−

Розв

’язування. Використаємо формулу інтегрування за частинами.

Нехай

= .dxedv

x−

= Одержимо dxdu = ,

−

−= .

)exe(

dxe

dxxe

−=

−−

−

∫∫

2.8. Наближене обчислення визначених інтегралів

Знаходженню інтеграла, присвячені всі попередні викладки

цього розділу. Проте, як ми вже знаємо, є ряд функцій для яких пер-

вісну неможливо виразити в елементарних функціях. З іншого боку,

в застосуванні визначеного інтеграла, не обов’язково мати йому ві-

дповідний невизначений інтеграл. Достатньо мати його значення

або

знайти його певне чисельне наближення. Розглянемо деякі ме-

тоди наближеного обчислення визначених інтегралів.

◙ Розклад підінтегрального виразу

При знаходженні визначеного інтеграла розкладають підінтег-