Шинкарик М.І. Вища математика
Подождите немного. Документ загружается.


341
ральну функцію за формулами Тейлора або Маклорена і інтегруван-
ням розкладу знаходять відповідний інтеграла .
Приклад 24. Обчислити
∫
−
+
+
−
0
1
1x
dx
1x
1e
.
=
+
−+
+
+
+
+
+
+
=
+
−
∫∫
−−
+
dx
1x
1...
!3
)1x(
!2
)1x(
!1
1x
1
dx
1x
1e
0
1
32
0
1
1x
32,1...
!33
1
!22
1
!1
1
dx...
!3
)1x(
!2
1x
!1
1
0
1
2
≈+
⋅
+
⋅
+=+
+
+
+
+=
∫
−
)( .
◙ Інтегрування з допомогою таблиць
Ряд інтегралів є добре вивчені і для них складені таблиці. Це
так звані табульовані неелементарні “спеціальні” функції. Напри-
клад інтеграли Френеля:
dt
2
t
cos)х(С
x
0
2
∫
π
=
і dt
2
t
sin)х(S
x
0
2
∫
π
=
,
інтегральна показникова функція, інтегральні синус і косинус, фун-
кція Лапласа
dte
2
1
)x(
x
0
2
t
2
∫
−
π
=Φ
, і ін..
◙ Інтеграли, для яких знайдено точне значення визначеного
інтеграла, не знаходячи невизначеного інтеграла
Наприклад
1
2
0
p
)
2
p
(cos
2
xdxtg
−
π
ππ
=
∫
якщо )1p1( <<− ,
2lnxdxsinln
0
π−=
∫
π
, і ін.
◘
◘
◘
Чисельне інтегрування
Методи чисельного інтегрування дають наближене чисельне
значення визначеного інтеграла, якщо можливо обчислити
значення підінтегральної функції в деяких точках проміжку
інтегрування.
Нехай треба знайти
∫
b
a
dx)x(f . Проміжок інтегрування [a;b]
розбивають на
2n проміжків однакової довжини
Δ
і знаходять зна-
чення функції
)x(fy
ii
= в точках розбиття y
0
,
y
1
,
y
2
,
,
y
3
,...
y
2n .
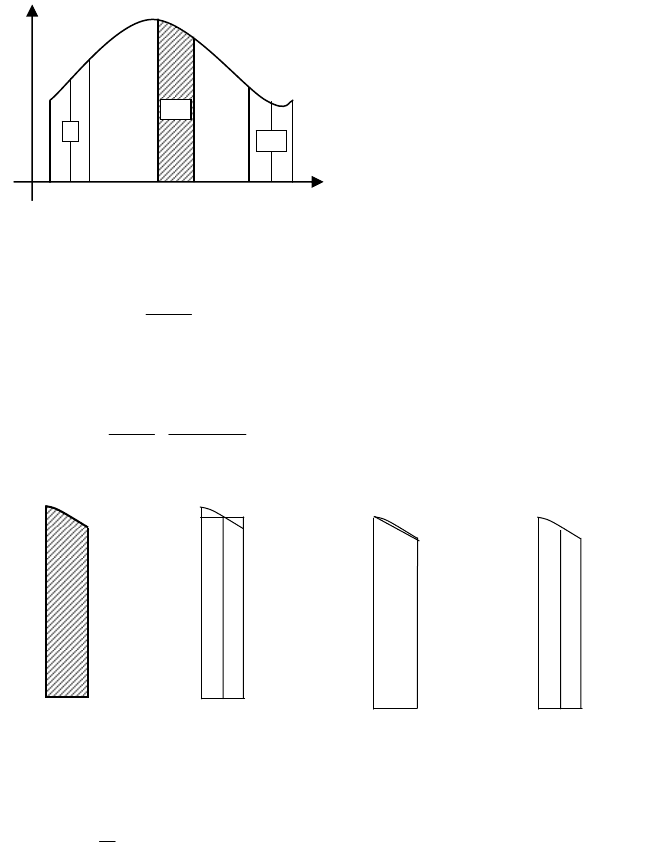
Тоді
342
1n21i2531
b
a
S...S...SSSSdx)x(f
−−
++++++=≈
∫
,
де
S
i
площа криволінійної тра-
пеції
(х
2і-2
,A
2і-2
,
A
2і
,
х
2і
)
. Виок-
ремимо криволінійну трапе-
цію
(х
2і-2
,A
2і-2
,
A
2і
,
х
2і
) (мал.6) і
будемо шукати її площу. Як-
що площу фігури (мал.7) (х
2і-2
,A
2і-2
,
A
2і
,х
2і
)
замінити площею
прямокутника з основою (х
2і-2
х
2і
)
то одержимо формулу
прямокутників наближеного
обчислення визначеного інте-
грала.
)y...y...yyy(
n
аb
Sdx)x(f
1n21i2531
b
a
−−
++++++
−
=≈
∫
(6.44)
Якщо ж дугу
A
2і-2
,
A
2і
замінити відрізком A
2і-2
,
A
2і
(мал.8) то фігура
(х
2і-2
,A
2і-2
,
A
2і
,
х
2і
) – трапеція, і одержуємо формулу трапецій
)y...yy
2
yy
(
n
аb
dx)x(f
1n231
n20
b
a
−
++++
+−
=
∫
(6.45)
Замінивши дугу
A
2і-2
,
A
2і-1
,
A
2і
частиною параболи, яка проходить
через точки
A
2і-2
,
A
2і-1
, A
2і
(мал.9) і знову обчисливши відповідну су-
му одержимо формулу Сімпсона (парабол). (6.46)
))y...yy(4)y...yy(2)yy((
3
dx)x(f
1n2312n242n20
b
a
−−
+++++++++
Δ
=
∫
х
2
і
А
2
і
х
2
і
-
2
А
2і-2
х
2
і
А
2
і
х
2
і
-
2
А
2і-2
А
2і-1
х
2
і
-
1
х
2
і
А
2
і
х
2
і
-
2
А
2і-2
А
2і-1
х
2
і
-
1
х
2
і
А
2
і
х
2
і
-
2
А
2і-2
мал.8
мал.6
мал.7
мал.9
Мал
. 5
х
2
n
-
2
A
2
n
-
2
х
2
n
-
1
A
2
n
-
1
A
1
х
2
і
-
2
х
1
х
2
х
2
і
A
2
і
-
2
A
2
і
A
0
A
2n
A
2
а
b
y
x
S
2i-1
S
1
S
2i-1
S
2n-1
343
Приклад 25. Обчислити
∫
+
1
0
2
dx
х1
1
.
Розв
’язування. Використаємо формулу Сімпсона. Запишемо
.5,0y;8,0y;1y;1x;5,0x;0x;5,0;2n
210210
=======Δ=
783,0)8,045,01(
3
5,0
dx
х1
1
1
0
2
≈⋅++≈
+
∫
. Збільшуючи кількість
точок розбиття, досягають необхідної точності обчислень.
§3. Невласні інтеграли та їх знаходження
При означенні
∫
b
a
dx)x(f
передбачалось виконання умов:
1. проміжок інтегрування
[]
b,а
- скінчений.
2. підінтегральна функція
f(x) визначена і неперервна на
[]
b,а .
В випадку коли хоча б одна з умов не виконується, інтеграл
називається невласним. Розглянемо два найпростіші випадки.
3.1. Інтеграл з нескінченними межами інтегрування
Означення 6. Нехай f(x) визначена на
[
)
∞,а і інтегровна на
[]
Z,а
, де
[]
Z,а
-будь- який скінчений проміжок. Тоді
∫∫
Ζ
∞→Ζ
∞
=
aa
dx)x(flimdx)x(f
, (6.47)
невласний інтеграл з нескінченними межами інтегрування.
За формулою Ньютона-Лейбніца
)a(F)Z(Fdx)x(f
Z
a
−=
∫
.
Якщо, при
∞→Z (
))a(F)Z(F −
має скінчену границю, то ця
границя буде визначена, і інтеграл даної функції на
(
a
,
∞
)
дорівнює )).a(F)z(F(limdx)x(flimdx)x(f
Z
Z
a
Z
a
−==
∞→∞→
∞
∫∫
Аналогічно розглядається і інтеграл виду
∫
∞−
в
dx)x(f
344
У випадку, коли потрібно обчислити інтеграл
∫
∞
∞−
dx)x(f його роз-
бивають на суму двох
∫∫∫
∞
∞−
∞
∞−
+=
c
c
dx)x(fdx)x(fdx)x(f і обчис-
люють кожен інтеграл окремо.
3.2. Інтеграл від розривної функції
Нехай
)x(f
визначена на
[
)
b,a і має точку розриву при
bx =
.
Отже
∫∫
ε−
→ε
=
b
a
0
b
a
dx)x(flimdx)x(f - відповідний невласний інтеграл
від розривної функції. Якщо
f(x) визначена на (a,b] і x=a точка роз-
риву, то
∫∫
ε+
→ε
=
b
a
0
b
a
dx)x(flimdx)x(f . Якщо ж )x(f має точку розри-
ву
()
b,aс ∈
, то
∫∫∫
ε+
→ε
ε−
→ε
+=
в
с
0
с
a
0
b
a
dx)x(flimdx)x(flimdx)x(f
.
Якщо для інтегралів пунктів (6.3.1) і (6.3.2) відповідні їм границі
існують, то інтеграли називаються збіжними. Якщо границі не іс-
нують або нескінченні, то інтеграли називаються розбіжними.
Приклад 26.
∞→
∞→∞→
∞
==
∫∫
1
Z
Z
1
Z
1
Z
xlnlimdx
x
1
limdx
x
1
. Це є розбіжний інтеграл.
Приклад 27. Обчислити
∫
∞
1
p
dx
x
1
Розв
’язування.
∫∫
∞→
∞
=
Z
1
p
Z
1
p
dx
x
1
limdx
x
1
. Досліджуємо цю границю:
якщо
р<1, ∞→
−
==
+−
∞→∞→
∞
∫∫
1
1
p
Z
Z
1
p
Z
1
p
Z
p1
x
limdx
x
1
limdx
x
1
;
p>1,
p1
1
0
p1
x
limdx
x
1
limdx
x
1
1
1
p
Z
Z
1
p
Z
1
p
Z
−
−=
−
==
+−
∞→∞→
∞
∫∫
;
p=1, ∞→
∞→∞→
∞
==
∫∫
1
Z
Z
1
Z
1
Z
xlnlimdx
x
1
limdx
x
1
.
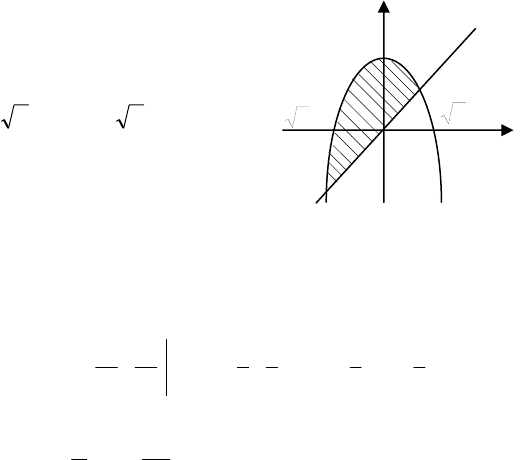
345
Значить, даний інтеграл розбіжний при p
≤
1 і збіжний при p>1. Його
часто використовують при дослідженні рядів на збіжність.
§ 4. Застосування визначених інтегралів
4.1. Обчислення площ
Площа фігури, яка обмежена графіком функції y=f(x) прямими
x=a і x=b, а також віссю Ox, визначається за формулою
∫
=
b
a
dx)x(fS . Площа ж фігури, яка обмежена графіками функцій
)x(fy
в
= та )x(fy
н
= ( )x(f)x(f
нв
≥ ), прямими
a
x
=
і bx =
визначається за формулою
∫
−=
b
a
нв
dx))x(f)x(f(S . (6.48)
Приклад 28. Знайти площу фігури, обмеженої лініями
у=2-х
2
,
у=х. (мал. 10).
Розв
’язування. а) Будуємо ескіз
графіків функцій:
у=2-х
2
,
( парабола, яка перетинає вісь Ох
в точках
А
1
(
2
;0)
і А
2
(-
2
;0
),
вершина параболи знаходиться в
точці
В(0;2)), у=х - пряма,
бісектриса 1- го і 3-го координат-
них кутів.
б) Знайдемо точки перетину графіків даних функцій (межі
інтегрування). Розв’яжемо рівняння: 2-х
2
=х; -х
2
-х+2=0.
Одержуємо розв’язки: х
1
= 1, х
2
= -2.
в) далі, за формулою (6.46) обчислюємо площу фігури:
2
9
)2
3
8
4()
2
1
3
1
2()
2
x
3
x
x2(dx)xx2(S
1
2
2
3
2
2
1
=−+−−−−=−−=−−=
∫
−
−
(кв. од.).
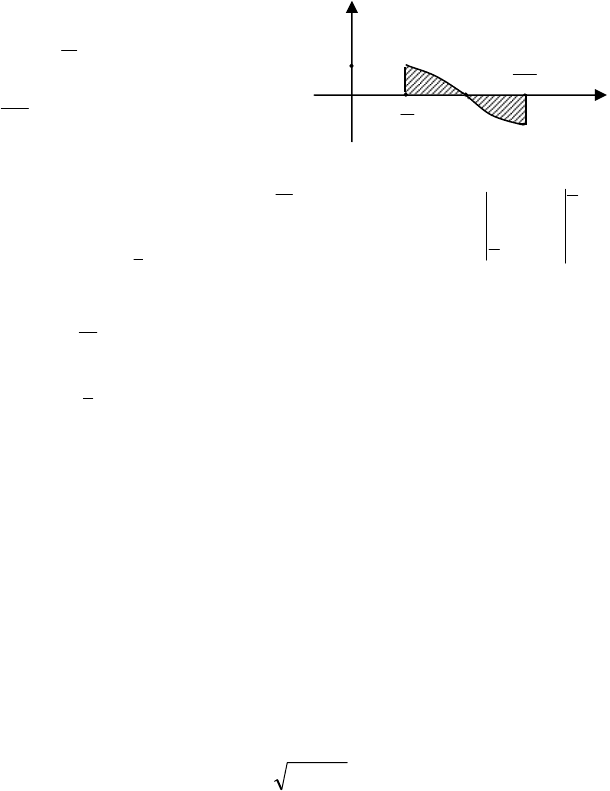
Приклад 29. Обчислити площу фігури, обмеженої лініями,
,xsiny =
у=0,
2
x
π
=
,
2
3
x
π
=
.
Розв’язування. Будуємо графіки функцій (мал.11). Записуємо фор-
)0;2(А
2
−
)2;0(В
)0;2(А
1
Мал. 10
346
мулу для знаходження площі
∫
−=
b
a
нв
dx))x(f)x(f(S . Бачимо, що
)x(f
в
записати одним виразом неможливо. Верхня межа даної площі,
складається з двох:
xsiny =
( на
інтервалі
);
2
( π
π
) та у=0 (на інтервалі
)
2
3
;(
π
π
).
π=
y
є нулем функції
xsiny =
. Тому
=+−=−+−=+=
π
π
π
π
π
π
π
π
∫∫
2
2
2
3
2
CDEABC
xcosxcosdx)xsin0(dx)0x(sinSSS
.)од.кв(2)10()01( =+++−−=
.
Інтеграл же
0dx)0x(sin
2
3
2
=−
∫
π
π
. Тому, при застосуванні визначеного
інтеграла, для знаходження площ, необхідно враховувати нулі функцій, які
обмежують площу (мал.3). Проміжок інтегрування, врахувавши нулі функцій,
розбивають, і тоді шукана площа дорівнює сумі абсолютних величин
відповідних визначених інтегралів.
4.2. Задача про розподіл доходів населення держави
Рівень розвитку держави характеризується тим, як вона забезпечує
рівень життя своїх громадян. Одним з таких показників є матеріальний
добробут. Легко і досить точно проводити такий порівняльний аналіз маю-
чи певні кількісні характеристики. Доброю характеристикою для цього є
коефіцієнт Джіні, який показує нерівність в розподілі
доходів населення.
Він безпосередньо зв’язаний з кривою Лоренца, яка відображає залежність
відсотка доходів населення від відсотка тих, які ці доходи мають. Розгля-
немо це на прикладі.
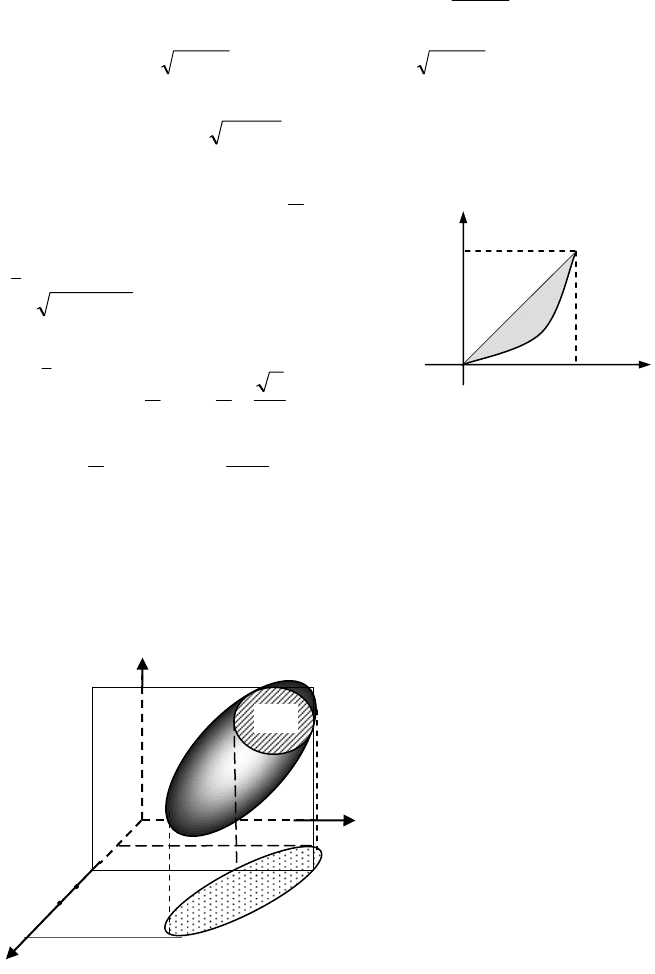
Приклад 30. Нехай
2
x42y −−=
, крива Лоренца, визначена за
дослідженнями розподілу доходів в якійсь країні, де
х-відсоток населення,
у – відсоток доходів населення. Обчислити ко-
ефіцієнт Джіні. (
0<k<1).
D
E
С
В
А
Мал.11
π
2
3
π
2
π
О
у
х
347
Розв’язування. З малюнка видно, що
OAB
OAm
S
S
k
Δ
=
,
∫∫∫∫
=−+−=−+−=
1
0
2
1
0
1
0
1
0
2
OAm
dxx4dx2xdxdx)x42x(S
Для знаходження
∫
−
1
0
2
dxx4 введемо заміну tsin2x = , тоді
нижня межа
t=0, а верхня
6
t
π
= .
Обчислюємо
41,0
2
3
3
2
2
1
dttcos4
dttcos2tsin12
6
0
2
6
0
2
≈+
π
+−==
=−
∫
∫
π
π
2
1
S
OAB
=
Δ
. Тому 82,0
5,0
41,0
k == . Великий коефіцієнт k показує
нерівномірність розподілу доходів серед населення даної країни.
4.3. Обчислення об’ємів
◘
◘
◘
Визначення і обчислення об’єму тіл за площами паралельних
перерізів
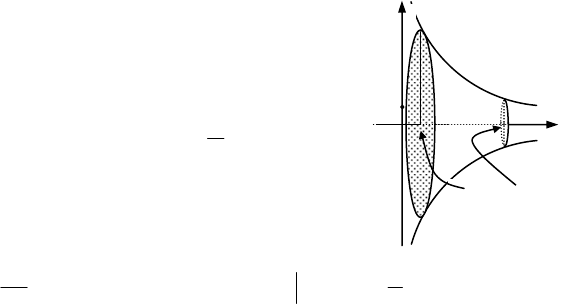
Нехай в просторі дано тіло, що знаходиться між двома пло-
щинами
a
x
=
і bx = , і
відомо, що всяка площина
паралельна до площини
zOy
і яка знаходиться від неї на
відстані
,
x
перетинає тіло по
плоскій фігурі, площа якої є
функція
)x(S
(мал. 12).
Спроектуємо тіло на площи-
ну
.xOy Одержимо плоску
фігуру, яку знову
спроектуємо на вісь
Ох (а<b).
Мал. 12
σ
1
О
a
b
x
n
-
1
x
2
x
1
y
z
x
S(x
1
)
100(1)%
Ч
астка
населення
Ч
астка
доходів
m
А
В
у
х
О
100(1)%
348
Розіб’ємо проміжок
[]
b,a
точками
1n21
x,...x,x
−
. Через точки поділу
проведемо перпендикулярні площини
1n321
,...,,
−
σσσσ до площини
xOy і позначимо )x(S),...x(S),x(S
1n21 −
- площі відповідних пара-
лельних один одному перерізів. Побудуємо на кожному перерізі, як на
основі, циліндр висотою, відповідно,
1
xΔ ,
2
xΔ , .xxx
1iii −
−=Δ Таким
чином одержимо
n
циліндрів. Запишемо суму, яка є інтегральною:
.x)x(Sx)x(S...x)x(Sx)x(Sx)x(S
n
1i
iinn332211
∑
=
Δ=Δ++Δ+Δ+Δ
Перейдемо до границі при
.0xmax
i
→Δ
Одержимо
[]
∫
=Δ++Δ+Δ+Δ=
→Δ
b
a
nn332211
0xmax
dx)x(Sx)x(S...x)x(Sx)x(Sx)x(SlimV
i
Якщо така границя існує, то кажуть, що дане тіло має об’єм.
◘
◘
◘
Обчислення об’єму тіла обертання
Нехай криволінійна трапеція утворена лінією
)x(fy =
, прямими
х=а та х=b та віссю Ох, обертається в просторі навколо осі Ох. Знайти
об’єм фігури обертання, яка утворилась.
Враховуючи те, що для об’єму тіла обертання площа поперечного перерізу
)x(f)x(S
2
π=
одержимо
∫∫
π=π=
b
a
2
b
a
2
.dx)x(fdx)x(fV (6.49)
Якщо ж криволінійна трапеція утворена лінією
)y(x
ϕ
= , прямими
у=с та у=d та віссю Оу, обертається в просторі навколо осі Оу то
∫∫
ϕπ=πϕ=
d
c
2
d
с
2
.dy)y(dy)y(V
Приклад 31. Знайти об’єм тіла
утвореного обертанням навколо осі абсцис
фігури, обмеженої лініями
x
4
y =
, х=1, х=4.
Розв’язування. Об’єм тіла обертання
обчислюємо за формулою
∫
π=
b
a
2
dxyV .
.)од.куб(12)1
4
1
(16)x(16dxx16dx
x
16
V
1
4
4
1
12
4
1
2
π=−π−=π−=π=π=
∫∫
−−
х
Мал. 13
0
у
1
1
4
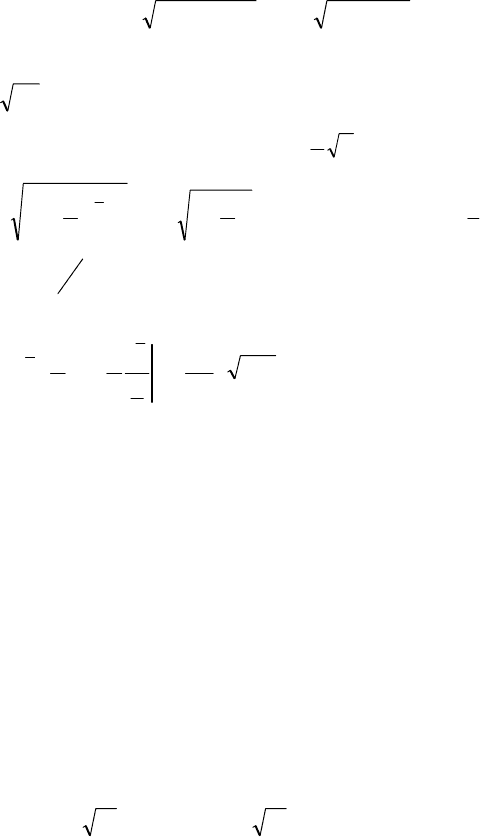
349
4.4. Обчислення довжини дуги плоскої кривої
Запишемо, без виведення, формулу для знаходження дуги
плоскої кривої, заданої рівнянням
y=f(x), при умові неперервності
на
[]
b,a
функцій
)x(f
і
)x(f
′
.
∫∫
′
+=
′
+=
b
a
2
b
a
2
.dx)y(1dx)x(f1L
(6.50)
Приклад 32. Знайти довжину дуги плоскої кривої лінії
3
xy = від точки О(0;0) до точки М(4;8).
Розв’язування. В задачі а=0, b=4, x
2
3
y =
′
. Тоді
dxx
4
9
1dx)x
2
3
(1L
4
0
4
0
2
2
1
∫∫
+=+= . Введемо заміну
tx
4
9
1 =+
.
Тоді
dt
9
4
dx =
. Змінимо межі інтегрування. Якщо 1t = , то 0x = ;
якщо t=10, то x=4. Обчисливши інтеграл, одержуємо довжину дуги:
.)довж.од(2,9)110(
27
8t
9
4
dt
9
4
tL
3
2
3
10
1
2
1
2
3
≈−==⋅=
∫
4.5. Задача про максимізацію прибутку за часом
Метою всякого виробництва є досягнення максимального
прибутку. Тобто, досягнення максимальної різниці між доходами і
видатками. Позначимо
P(t), D(t), V(t) – відповідно функції прибутку,
доходу та видатків від часу. Тоді
P(t)=D(t)-V(t). Функція досягає
свого екстремуму, якщо її похідна рівна 0. Тобто
0)t(V)t(D)t(P =
′
−
′
=
′
. Тобто
)t(V)t(D
′
=
′
. Визначимо момент
t
k
в який
швидкість зміни доходу та видатків зрівнюються. Загаль-
ний прибуток за час
t
k
можна знайти за формулою
∫∫
′
−
′
=
′
=
kk
t
0
t
0
k
dt))t(V)t(D(dt)t(P)t(P .
Приклад 33. Швидкості зміни витрат і доходу підприємства,
після початку його діяльності визначались формулами:
4
3
4
3
t29)t(D,t25)t(V −=
′
+=
′
, V і
D
вимірювали у мільйонах
1
10
350
гривень, а
t
у роках. Визначити тривалість прибуткового існування
підприємства і знайти загальний прибуток, одержаний за цей час.
Розв
’язування. Оптимальний час
1
t
для прибутку
підприємства одержимо з умови
)t(V)t(D
′
=
′
. З рівняння
4
3
4
3
t29t25 −=+ визначаємо
1t,1t,4t
1
4
3
4
3
=== 4
.
Отже, підприємство було прибутковим 1 рік. За цей час одержано
прибутку:
()
=−−−=
′
−
′
=
∫∫
dtt25t29dt)t(V)t(DP
1
0
4
3
4
3
1
0
][
).(
7
3
3
7
4
4
t
t4dtt44
0
1
4
7
4
7
1
0
4
3
грн.млн.=−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅−=
⎟
⎠
⎞
⎜
⎝
⎛
−
∫
4.6. Задача про витрати, дохід і прибуток
Нехай тепер V(х) – функція загальних видатків на виробниц-
тво
х одиниць продукції, )х(V
′
- функція маржинальних видатків.
)х(D),х(P
′′
- функції, відповідно, маржинальних прибутку та до-
ходу. Тоді при зростанні кількості одиниць продукції від
a до b,
зміна загальних видатків обчислюється за формулою
)a(V)b(V)x(Vdx)x(V
a
b
b
a
−==
′
∫
.
При зростанні реалізації продукції зміни прибутку і доходу
визначимо за формулами:
)a(P)b(P)x(Pdx)x(P
a
b
b
a
−==
′
∫
,
)a(D)b(D)x(Ddx)x(D
a
b
b
a
−==
′
∫
.
§ 5. Поняття про подвійний інтеграл. Зведення
подвійного інтегралу до повторного
5.1. Поняття про подвійний інтеграл
При введені поняття визначеного інтеграла ми розв’язували задачу про
знаходження площі криволінійної трапеції. Проте, часто необхідно знайти об’єм
деякої просторової фігури. Розв'яжемо задачу: знайти об’єм тіла обмеженого
