Шинкарик М.І. Вища математика
Подождите немного. Документ загружается.

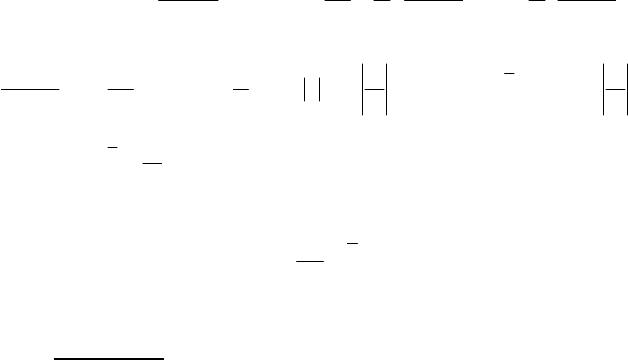
361
Розв’язування. Заміною
xu
y
=
зведемо задане рівняння до рі-
вняння
u21
uu
uxu
2
−
−
=
′
+
або
u21
u
x
1
)u
u21
uu
(
x
1
dx
du
22
−
⋅=−
−
−
=
.
Відокремлюючи змінні , знайдемо
x
dx
du
u
u21
2
=
−
, звідки
x
C
lnuln2
u
1
=+
або
x
C
lnueln
2
u
1
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅ ,
тобто
x
C
eu
u
1
2
=⋅
.
Повертаючись до змінної
y
, одержимо загальний розв’язок:
Ce
x
y
y
x
2
=⋅ .
2.4.Лінійні диференціальні рівняння
Означення. Лінійним диференціальним рівнянням першого
порядку називається рівняння , яке містить шукану функцію і її
похідну у першому степені без їх добутку:
y′+P(x)y=Q(x). (7.13)
Тут P(x), Q(x)- відомі функції незалежної змінної x. Напри-
клад,
.xxy2y
2
=+
′
Якщо Q(x)=0, то рівняння (7.13) називається лінійним одно-
рідним і є рівнянням з відокремлюваними змінними.
Якщо Q(x)≠0 , то рівняння (7.13) називається лінійним неод-
норідним, яке можна розв’язати декількома способами.
Розглянемо метод Бернуллі за допомогою якого рівняння
(7.13) можна звести до інтегрування двох диференціальних рівнянь
першого порядку з відокремлюваними змінними.
Розв’язок диференціального рівняння
(7.13) шукаємо у ви-
гляді y=u(x) v(x) або y=uv, (7.14)
де u(x), v(x) невідомі функції. Одну з цих функцій можна взяти до-
вільну, а інша визначається із рівняння (7.13).
Із рівності y=uv знайдемо похідну y′:
vuvuy
′
⋅+⋅
′
=
′
.
Підставимо
у
та y
′
в рівняння (7.13):
)x(Qvu)x(Pvuvu =⋅⋅+
′
+
′
або ).x(Q)v)x(Pv(uvu =⋅+
′
+
′
Виберемо функцію
v
такою, щоб
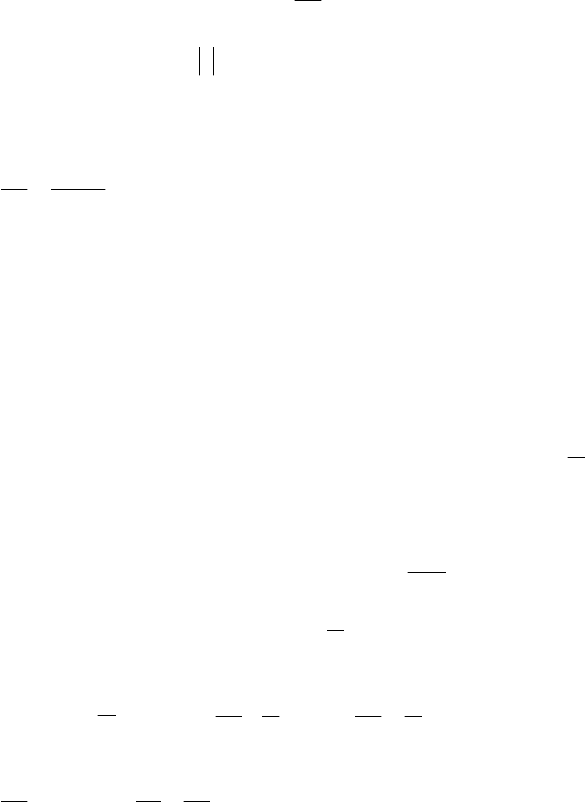
362
0v)x(Pv =+
′
. (7.15)
Тоді для відшукання функції
u одержимо рівняння
)x(Qvu =
′
. (7.16)
Спочатку знайдемо
v із рівняння (7.15).
Відокремлюючи змінні, маємо
dx)x(P
v
dv
−=
, звідки
∫
−= dx)x(Pvln або
∫
=
− dx)x(P
ev
.
Під невизначеним інтегралом тут будемо розуміти якусь одну
первісну від функції P(x), тобто v буде визначеною функцією від x.
Знаючи v, знаходимо u із рівняння (7.16):
∫
⋅==
dx)x(P
e)x(Q
v
)x(Q
dx
du
; dxe)x(Qdu
dx)x(P
⋅=
∫
,
звідки
∫
+=
∫
.Cdxe)x(Qu
dx)x(P
Тут ми вже беремо для u всі первісні.
Знайдені функції u та v підставляємо в (7.14) і одержуємо
загальний розв’язок лінійного диференціального рівняння:
∫
+=⋅=
∫∫
−
)Cdxe)x(Q(evuy
dx)x(Pdx)x(P
. (7.17)
При розв’язуванні конкретних прикладів простіше виконувати
ці викладки, ніж застосовувати громіздку формулу (7.17).
Приклад 1. Розв’язати диференціальне рівняння .x
x
y
у =−
′
Розв
’язування. Розв’язок шукаємо у вигляді y=uv, тоді
vuvuy
′
⋅+⋅
′
=
′
.
Підставимо
у
та
y
′
в рівняння:
x
x
vu
vuvu =
⋅
−
′
+
′
або
x)
x
v
v(uvu =−
′
+
′
. (7.18)
Вираз, що стоїть у дужках прирівнюємо до нуля, маємо
0
x
v
v =−
′
або 0
x
v
dx
dv
=−
; .
x
v
dx
dv
=
.
Відокремимо змінні, домноживши обидві частини рівняння на
,
v
dx
тоді
x
dx
v
dv
=
.
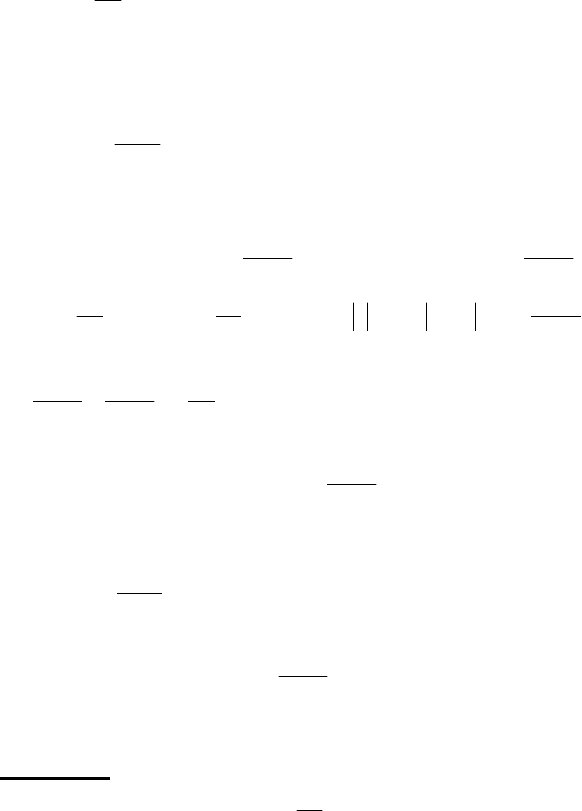
363
Після інтегрування , одержимо
ln
|
v
|
=ln
|
x
|
( тут обмежимось
однією первісною), звідки v=x.
Підставимо v=x в рівняння (7.18):
;xvu =
′
;xx
dx
du
=⋅ dxdu =
; .Cxu +=
Загальний розв’язок запишеться:
.Cxx)Cx(xy
2
+=+=
Приклад
2. Знайти частинний розв’язок диференціального рі-
вняння
xcos
1
ytgxy =−
′
, який задовольняє початковій умові y(0)=0.
Розв
’язування. Задане рівняння – це лінійне неоднорідне рів-
няння першого порядку, розв’язок якого шукаємо у вигляді
v
u
y
⋅=
.
Тоді
;
xcos
1
uvtgxvuvu =−
′
+
′
;
xcos
1
)vtgxv(uvu =−
′
+
′
;0vtgxv =−
′
;0vtgx
dx
dv
=−
tgxdx
v
dv
=
; xcoslnvln −= ;
xcos
1
v =
.
Підставимо
v
в рівняння і знайдемо
u
:
;
xcos
1
xcos
1
u =⋅
′
;1
dx
du
=
dxdu =
;
Cxu +=
.
Загальний розв’язок диференціального рівняння буде :
.
xcos
1
)Cx(y ⋅+=
Підставляємо початкові умови в знайдений розв’язок
і знаходимо С:
;
0
сos
1
)
С0(0 ⋅+=
.0C =
Із загального розв’язку одержуємо частинний розв’язок
.
x
cos
x
y =
2.5. Диференціальне рівняння Бернуллі
Означення. Рівняння вигляду
)x(Qyy)x(Py
n
=+
′
(або
)y(Qxx)y(P
dy
dx
n
=+
)
називається диференціальним рівнянням Бернуллі.
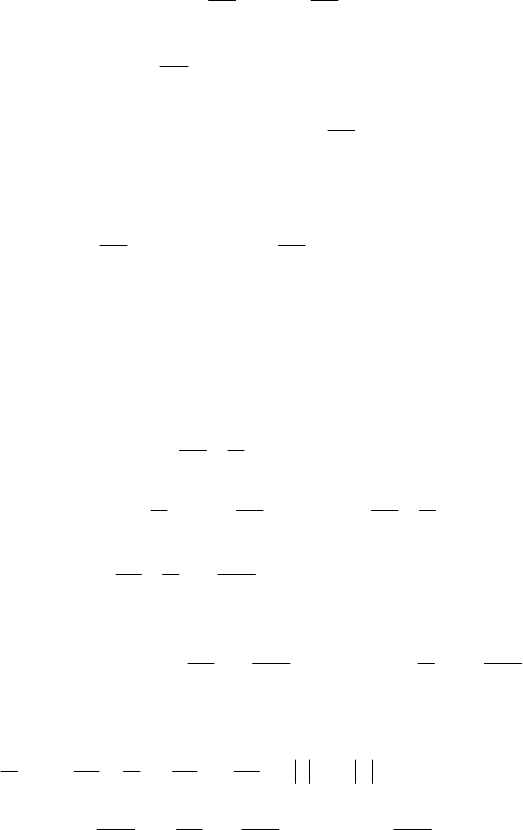
364
Дане рівняння відрізняється від рівняння (7.13) лише множ-
ником
y″ (або x″) в правій його частині. Для того, щоб права части-
на даного рівняння була такою як в (7.13), поділимо його ліву і пра-
ву частину на
y″:
)x(Q
y
y
)x(P
y
y
nn
=+
′
.
Зробимо заміну:
1n
n
y
y
y
z
+−
== ; ;yy)n1(z
n
′
⋅−=
′
−
n
y
y
)1n(z
′
+−=
′
.
Домножимо ліву і праву частини одержаного рівняння на
(n+1) і, використовуючи заміну, матимемо:
)x(Q)1n(
y
y
)x(P)1n(
y
y
)1n(
nn
+−=+−+
′
+−
;
).x(Q)1n(z)x(P)1n(z +−=+−+
′
Ми одержали лінійне диференціальне рівняння відносно нової
змінної
z=y
-n+1
.
Приклад 1.
Знайти загальний розв’язок диференціального рів-
няння
xlnyyyx
2
=+
′
.
Розв’язування.
xln
y
1
y
y
x
2
=+
′
Зробимо заміну
,
y
1
z =
2
y
y
z
′
−=
′
. Тоді
;xln
y
1
y
y
x
2
=+
′
⋅−
;xlnzzx −=−
′
x
xln
x
z
dx
dz
−=−
.
Дане рівняння розв’яжемо, зробивши заміну
)x(v)x(uz ⋅= .
;uvvuz
′
+
′
=
′
;
x
xln
x
uv
uvvu −=−
′
+
′
.
x
xln
)
x
v
v(uvu −=−
′
+
′
Вибираємо функцію
v(x) так, щоб вираз в дужках дорівнював
нулю і ця функція була б частинним розв’язком рівняння
;0
x
v
v =−
′
;
x
v
dx
dv
=
;
x
dx
v
dv
∫∫
= ;xlnvln =
.
x
v
=
Тоді,
;
x
xln
xu −=⋅
′
;
x
xln
dx
du
2
−= Cdx
x
xln
du
2
+−=
∫∫
.
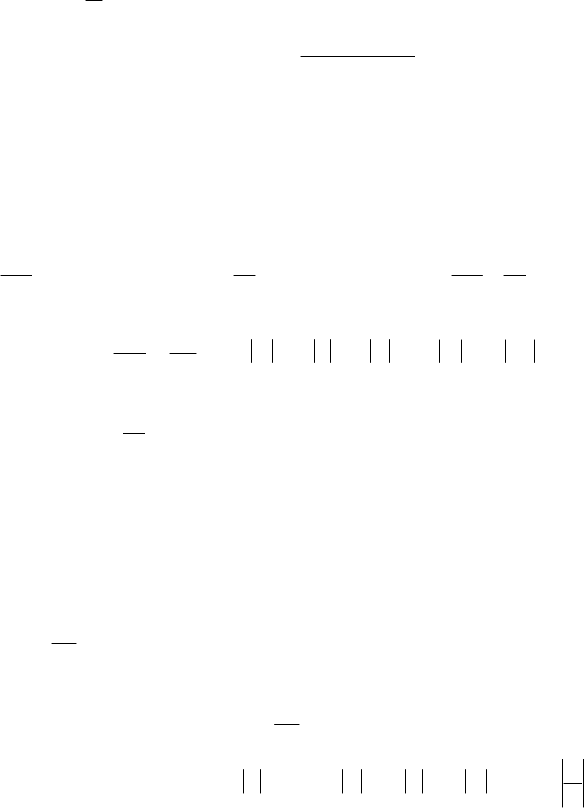
365
Проінтегрувавши праву частину цього рівняння за частинами, одер-
жимо
C)1x(ln
x
1
u ++=
, а при uvzy
1
==
−
, маємо
.
1
x
ln
Cx
1
y
++
=
2.6. Економічні задачі, що приводять до диференціальних
рівнянь першого порядку
Задача 1. Повні затрати К є функцією об’єму виробництва x.
Знайти функцію К затрат, якщо відомо, що швидкість росту затрат
для всіх значень x дорівнює середнім затратам.
Розв
’язування. Швидкість росту затрат є похідна:
dx
dK
, а середні затрати
.
x
K
За умовою задачі
dx
dK
=
x
K
, а це рів-
няння з відокремлюваними змінними.
Отже,
x
dx
K
dK
=
;
ClnxlnKln +=
;
;CxlnKln =
K=Cx - шукана функція затрат.
Звідси,
C
x
K
=
- середні затрати постійні.
Задача
2. Кількість населення у є функцією часу t, тобто з ча-
сом кількість населення змінюється. Швидкість зміни приросту на-
селення пропорційна кількості населення. Треба знайти формулу
для визначення кількості населення у будь-який момент часу t.
Розв
’язування. За умовою задачі швидкість зміни приросту
населення пропорційна кількості населення. Це можна записати так:
)t(yk
dt
dy
⋅=
, де k - коефіцієнт пропорційності.
В одержаному диференціальному рівнянні відокремимо змінні:
.kdt
y
dy
=
Далі будемо мати:
;Clnktyln +=
ktClnyln =−
;
;kt
C
y
ln =
.Cey
kt
=
(7.19)
Одержано формулу для визначення кількості населення як
функції часу. Вона містить довільну сталу, яка може приймати будь-
які числові значення.
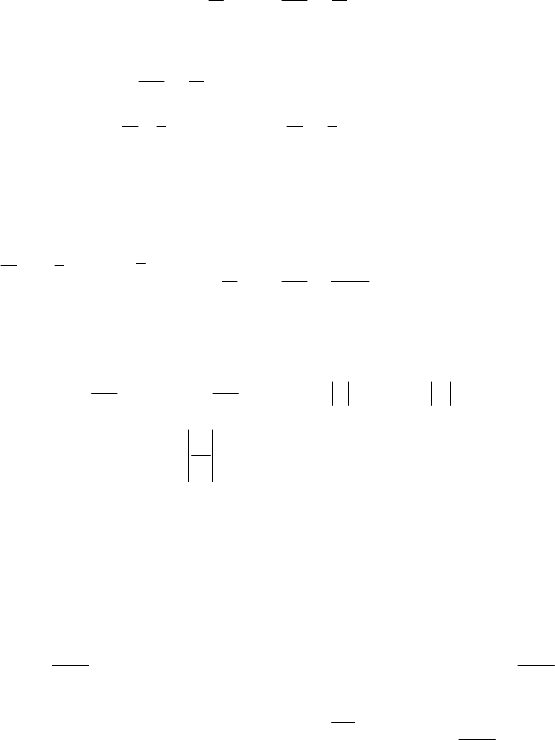
366
Покажемо на прикладі як за формулою (7.19) можна прогно-
зувати ріст населення. Для зручності візьмемо наближені дані.
Нехай за переписом 1980 року населення на Землі було, на-
приклад, 5 млрд. Почнемо звідси відлік, тобто
t
0
=0. А в 1990 році
населення на Землі стало 6 млрд. , тобто
t=10 (років). Тоді, викорис-
тавши ці початкові умови, одержимо:
5=С·е
k·0
; C=5.
Підставимо знайдене
C=5 у формулу y=Ce
kt
, маємо
;e56
k10⋅
⋅=
;
5
6
lnk10 ==
5
6
ln
10
1
k =
.
Ми знайшли коефіцієнт пропорційності.
Враховуючи, що
5
6
ln
10
1
k
=
, формулу
kt
Cey = запишемо у вигляді
t
5
6
ln
10
1
e5y
⋅⋅
=
або
⋅⋅
=
5
6
lnt
10
1
e5y
. (7.20)
Формула (7.20) дає можливість знайти кількість населення у
будь-який момент часу
t
, наприклад, знайдемо кількість населення
у 2010 році (
t
=30 ):
.)млрд(6,8
25
216
5
6
5
6
5e5e5y
2
3
3
3
5
6
5
6
ln30
10
1
≈==
⎟
⎠
⎞
⎜
⎝
⎛
⋅=⋅==
⎟
⎠
⎞
⎜
⎝
⎛
⋅⋅⋅
Задача
3. Нехай в момент часу t величина вкладу в банк
g=g(t)
. Очевидно, що збільшення (зміна) вкладу пропорційне його
величині:
);t(kg
dt
dg
=
;kdt
g
dg
=
Clnktgln += ;
;kt
C
g
ln =
kt
eCg ⋅= . (7.21)
Нехай при
t=0 початковий вклад в банк був g
0
, тоді
0
0
Ceg =
і
формула (7.21) запишеться:
kt
0
egg = . (7.22)
Нехай величина вкладу змінюється неперервно з часом і за мі-
сяць зростає на
N %:
(egg
100
N
g
1k
000
⋅
=⋅+
t
=1 місяць ) , звідки
.
100
N
1lnk
⎟
⎠
⎞
⎜
⎝
⎛
+=
Підставимо
k у (7.22): ;
100
N
1gegg
t
0
100
n
1ln
0
t
⎟
⎠
⎞
⎜
⎝
⎛
+=⋅=
⎟
⎠
⎞
⎜
⎝
⎛
+

367
Остання формула дає можливість визначити величину вкладу
в банк в будь- який момент часу
t.
Задача
4. Зростання інвестицій.
Економісти встановили, що швидкість зростання інвестовано-
го капіталу у будь-який момент часу t пропорційна величині капіта-
лу із коефіцієнтом пропорційності ,що дорівнює узгодженому відсо-
тку R неперервного зростання капіталу. Треба знайти закон зрос-
тання інвестованого капіталу, враховуючи величину початкової
(при
t
=0 ) інвестиції K
0
.
Розв
’язування. Позначимо K(t) - величина інвестованого капі-
талу у момент часу
t
(шукана функція).
Тоді
dt
)t(dK
- швидкість зміни величини інвестицій,
100
R
r =
.
За умовою задачі маємо:
)t(Kr
dt
)t(dK
⋅=
;
0
0t
K)t(K =
=
.
Одержали задачу Коші для диференціального рівняння пер-
шого порядку. Загальним розв’язком диференціального рівняння
буде функція
rtCCrt
eee)t(K ⋅==
+
.
Згідно з початковою умовою при
t
=0 маємо
C
0
eK =
.
Отже, розв’язком задачі буде функція
rt
0
eK)t(K ⋅=
.Це озна-
чає, що за даними умовами задачі інвестиції з часом зростають за
експоненціальним законом.
Задача
5. Відомо, що еластичність попиту
η
визначається за
формулою
dp
dx
x
р
⋅=η
, де
x
- кількість одиниць деякого товару вар-
тістю
p за кожну одиницю. Знайти функцію попиту на цей товар,
якщо еластичність попиту постійна і дорівнює
-1.
Розв
’язування. За умовою задачі: 1
dp
dx
x
р
−=⋅ ;
;
p
dp
x
dx
−=
Clnplnxln +−=
;
p
C
lnxln =
;
;
p
C
x =
.
x
C
p =
Знайшли залежність між кількістю товару та його вартістю,
тобто функцію попиту.

368
§ 3. Диференціальні рівняння другого порядку
Означення. Диференціальним рівнянням другого порядку
називається рівняння, яке зв’язує незалежну змінну
x
, невідому
функцію
y
та першу і другу похідні від цієї функції:
0)y,y,y,x(F =
′′′
. (7.23)
Означення. Загальним розв’язком диференціального рівняння
другого порядку називається функція y=φ(x,C
1
,C
2
) яка задовольняє
диференціальне рівняння при довільних значеннях C
1
та C
2
.
Будь-який частинний розв’язок диференціального рівняння
одержується із загального розв’язку при певних значеннях
C
1
та C
2
і
задовольняє певним початковим умовам. Початковими умовами для
диференціального рівняння другого порядку є задання значень функ-
ції та її першої похідної в деякій точці
x
0
:
0xx
yy
0
=
=
і
0xx
yy
0
′
=
′
=
.
Задача Коші для диференціального рівняння другого порядку
формулюється так:
знайти
частинний розв’язок диференціального рівняння
(7.23),
який задовольняє початковим умовам .
Геометричний зміст частинного розв’язку – це інтегральна
крива, яка проходить через точку
(x
0
,y
0
) в даному напрямку, тобто
заданий кутовий коефіцієнт дотичної до інтегральної кривої.
Розглянемо задачу, яка приводить до диференціального рів-
няння другого порядку.
Згідно теорії Дж. Хікса, із стабільним ростом затрат праці при
незмінних інших факторах виробництва вартість випуску продукції
також зростає . Швидкість її зростання є постійною додатною вели-
чиною
V
0
. Однак, додаткове залучення фактору затрат праці веде до
зниження граничного значення випуску продукції, причому темпи
такого зниження можна вважати постійною від’ємною величиною
a
0
.
Нехай початковий випуск продукції характеризується вартіс-
тю
C
0
при затратах праці L
0
. Треба знайти величину вартості випус-
ку продукції при затратах праці рівних
L
1
.
).55L;50L;01,0a;5,0V;100C(
10000
==−===
Позначимо
U(L) - вартість випуску продукції при затратах
праці рівних
L
. Тоді
dL
dU
- швидкість зростання вартості продукції
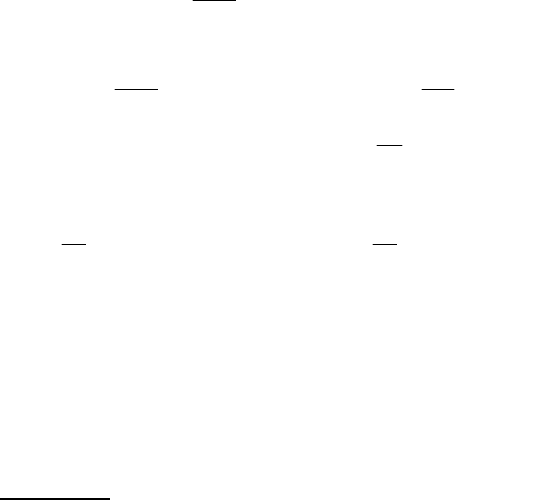
369
.aLa
2
L
aU
21
2
0
++=
відносно затрат праці L;
2
2
dL
Ud
- темпи зміни швидкості зростання
вартості продукції відносно затрат праці
L.
За умовою задачі
0
2
2
a
dL
Ud
=
, проінтегруємо по :L
10
aLa
dL
dU
+= ,
ще раз проінтегруємо по
L
, маємо:
Визначимо сталі
1
a та :a
2
⎪
⎩
⎪
⎨
⎧
−=
−+=
⇔
⎪
⎩
⎪
⎨
⎧
+=
++⋅=
.LaVa
,LVL
2
a
Ca
.aLaV
,aLaL
2
a
C
0001
00
2
0
0
02
1000
201
2
0
0
0
У нашому випадку одержимо
.1a;5,62a
12
==
Отже,
5,62LL005,0U
2
++−= , звідки
375,1025,625555005,0)L(U
2
1
=++⋅−=
3.1
Лінійні однорідні диференціальні рівняння другого по-
рядку
Означення. Лінійним однорідним диференціальним рівнян-
ням другого порядку називається рівняння
0y)x(g'y)x(p''y =++ . (7.24)
Очевидно, що
y
≡
0 є розв’язком рівняння (7.24). Цей розв’язок
називають нульовим або тривіальним. Надалі ми будемо шукати
тільки нетривіальні розв’язки диференціального рівняння (7.24).
Встановимо деякі властивості його розв’язків.
1. Якщо
y(x) є розв’язком рівняння (7.24), то Cy(x) також є
розв’язком цього рівняння.
2. Якщо
y
1
(x) та y
2
(x) - частинні розв’язки рівняння (7.24), , то
)x(y)x(y
21
+ є також розв’язком цього рівняння.
ТЕОРЕМА
. Якщо y
1
(x) та y
2
(x) - частинні розв’язки рівня-
ння (7.24), то розв’язком цього рівняння є також функція
)x(yC)x(yCy
2211
+= (7.25)
Доведення. Підставимо функцію (7.25) в рівняння(7.24), має-
мо:
+
′
+
′
+
′′
+
′′
))x(yC)x(yC)(x(p)x(yC)x(yС
22121
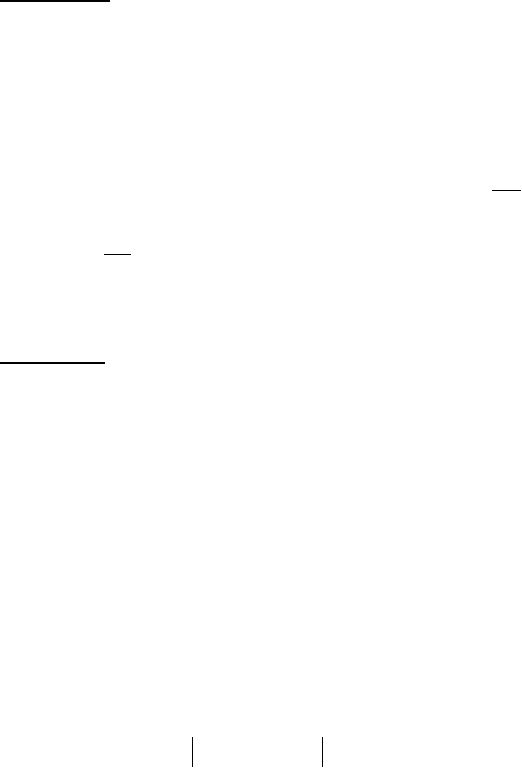
370
)).x(y)x(g)x(y)x(p)x(y(C
))x(y)x(g)x(y)x(p)x(y(C))x(yC)x(yC)(x(g
2222
1111221
+
′
+
′′
+
++
′
+
′′
=
′
+
′
+
Вирази в дужках тотожно рівні нулю, бо )x(y
1
та )x(y
2
- роз-
в’язки рівняння (7.24), а це означає, що права частина рівняння до-
рівнює нулю. Отже, функція (7.25) є розв’язком рівняння (7.24).
Означення. Система функцій )x(y
1
та )x(y
2
називаєть-
ся лінійно незалежною на відрізку
[]
b,a , якщо рівність
0yCyС
2211
≡+ (7.26)
виконується для всіх
x
тоді і тільки тоді, коли .0CC
21
==
Якщо рівність (7.26) виконується, коли хоча б один із 0C
i
≠ ,
то система
називається лінійно залежною.
Нехай
0yCyС
2211
≡+ ; якщо 0С
1
≠ , тоді
2
1
2
1
y
C
C
y −=
або
21
yy λ= , звідки
λ=
2
1
y
y
, де λ - стале число.
Іншими словами, дві функції лінійно залежні тоді і тільки то-
ді, коли вони пропорційні.
Означення. Лінійно незалежна система розв’язків лінійного
однорідного диференціального рівняння називається фундамен-
тальною системою розв’язків.
ТЕОРЕМА (про структуру розв’язку однорідного дифере-
нціального рівняння). Якщо )x(y
1
та )x(y
2
утворюють фун-
даментальну систему розв’язків рівняння (7.24), то
)x(yC)x(yСy
2211
+= , де
21
C,C - довільні сталі, є загальним
розв’язком рівняння (7.24).
Доведення. Відомо, що розв’язок називається загальним, якщо
з нього при певних числових значеннях сталих можна отримати
будь-який частинний розв’язок. А за теоремою про існування і єди-
ність будь-який частинний розв’язок однозначно визначається поча-
тковими умовами.
Покажемо, що можна знайти
C
1
і C
2
такі, щоб задовольнялись
початкові умови:
0xx
yy
0
=
=
,
0xx
yy
0
′
=
′
=
.
Нехай, коли
0
xx = , маємо:
