Шинкарик М.І. Вища математика

351

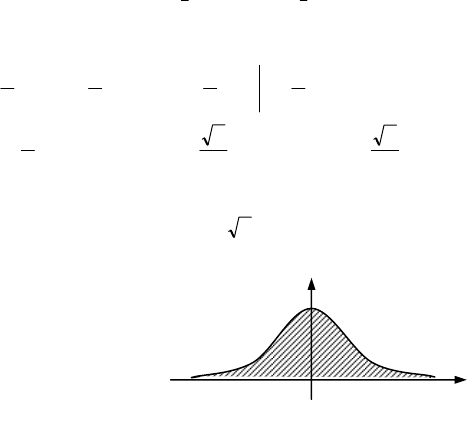
зверху неперервною поверхнею

)y,x(fz =

(

0)y,x(f ≥

), знизу скін-

ченою замкненою областю S площини

xOy, з боків прямою циліндричною

поверхнею побудованою на межі облас-

ті S, перпендикулярно до площини xOy.

Знайдемо об’єм V тіла зображеного на

малюнку 14. Розіб’ємо область S дея-

кими лініями на n частин з площами

відповідно S

1

, S

2

... S

n

.В кожній з частин

виберемо по одній точці P

1

(x

1

,y

1

),

P

2

(x

2

,y

2

)…P

n

(x

n

,y

n

) і побудуємо

циліндри з основами S

i

і висотами P

i-

Q

i

=f(x

i

,y

i

). Тоді об’єм V

222111i

n

1i

ii

...S)y,x(fS)y,x(fS)y,x(fV

+

++=⋅=

∑

=

. (6.51)

Ця сума називається двомірною інтегральною сумою для функції )y,x(fz = по

області S. Для цієї суми виконується теорема існування подвійного інтеграла:

Якщо функція,

)y,x(fz =

неперервна в обмеженій замкнутій області S і якщо

число частинок n, на які розбита область S, необмежено зростає, а найбільша

відстань між двома точками кожної частинки, які лежать на границі (

i

diamS

) ,

прямує до 0, то існує границя двомірної інтегральної суми (6.50), вели-

чина якої не залежить ні від способу розбиття S ні від вибору точки P

i

всередині частинки з площею S

i

.

Ця границя називається подвійним інтегралом від функції )y,x(fz =

поширеним на область S і позначається

∫∫

S

dxdy)y,x(f

. Тобто

∑

∫∫

=

→

∞→

=

n

1i

iii

0diamS

n

S

S)y,x(flimdxdy)y,x(f

i

.

Треба зазначити, що якщо

0diamS

i

→

, то автоматично ∞→

n

. Тому можна запи-

сати

∑

∫∫

=

→

=

n

1i

iii

0diamS

S

S)y,x(flimdxdy)y,x(f

i

(6.52)

5.2. Повторний інтеграл. Перехід від подвійного інтеграла

до повторного

Підійдемо до задачі про знаходження об’єму V поверхні )y,x(fz = по ін-

шому. Врахуємо, що область S в площині xOy обмежена зверху і знизу певними

лініями

)x(y

1

ϕ=

і )x(y

2

ϕ= .Разом з тим, функції

)x(

1

ϕ

і )x(

2

ϕ неперервні на

[

аb]. Проведемо переріз нашого тіла площиною х= х

і

, паралельно до координатної

площини zOy так, що a<x<b. (мал..15) Площа перерізувизначається як деяка функ-

ція від х , тобто S=F(x).

P

i

Q

i

=

f

(

x

i

,

y

i

)

)y,x(fz =

О

y

z

S

i

Q

i

P

i

Мал

. 14

)x(

2

ϕ

)x(

1

ϕ

b

а

x

i

)y,x(fz =

О

y

z

x

S

і

=F(x

і

)

S

Мал

. 15

352

В такому випадку об’єм тіла

∫

=

b

a

dx)x(FV . (6.53)

Визначимо тепер функцію F(x). Так

dy)y,x(fS

)x(

ii

i2

i1

∫

ϕ

=

. А це значить, що

dy)y,x(fS)x(F

)x(

2

1

∫

ϕ

==

(6.54)

Об'єднавши формули (6.53) і (6.54) одержуємо

∫∫

ϕ

=

b

a

)x(

dxdy)y,x(fV

2

1

][

. (6.55)

Інтеграл (6.55) називається повторним інтегралом, поширеним на довільну

область S. Зауважимо, що якщо б область була обмежена кривими )y(x

1

ψ= і

)y(x

2

ψ= ( неперервними на (c,d)) то отримали б, що

∫∫

ψ

=

d

c

)y(

dydx)y,x(fV

2

1

][

, та-

кож повторний інтеграл.

Отже, обчислення подвійного інтеграла можна звести до обчислення повто-

рного.

5.3. Інтеграл Ейлера-Пуассона

В теорії ймовірності і математичній статистиці велику роль відіграє інтеграл

Ейлера-Пуассона: dxe

0

x

2

∫

∞

−

(6.56)

Він належить до інтегралів, які не виражаються в елементарних функціях.

Обчислимо його з допомогою подвійного інтеграла. Застосуємо формули зв’язку

між декартовими і полярними координатами

⎩

⎨

⎧

ϕ=

.sinry

.cosrx

Врахуємо те, що визначений інтеграл не залежить від позначення змінної

(інваріантність визначеного інтеграла відносно змінної).

Тому

можемо записати dye

0

y

2

∫

∞

−

(6.57)

Перемноживши формули (6.56) і (6.57) , одержимо

∫∫

∞∞

+−

=

00

)yx(2

dxdyeI

22

.

Врахувавши,що

2222222

rsinrcosryx =ϕ+ϕ=+ і

x

y

cosr

sinr

tg

=

ϕ

=ϕ ,

353

Одержимо:

=ϕ=ϕ=

−

π

∞∞

π

−

∞∞

+−

∫∫∫∫∫∫

rdreddrdredxdye

2222

r

2

000

2

0

r

00

)yx(

][

4

e

4

dre

4

rdre

2

0

r

0

2r

0

r

222

π

=

π

−=

π

=

π

=

∞

−

∞

−

∞

−

∫∫

][ .

З

одержаної рівності

4

I

2

π

=

визначаємо, що

2

I

π

=

. Тобто

2

dxe

0

x

2

π

=

∫

∞

−

.

А тепер визначимо інтеграл Ейлера-Пуасона

π==

∫∫

∞

−

∞

∞−

−

dxe2dxe

0

xx

22

(6.58)

Геометрично, інтеграл Пуассона виражає

собою площу фігури (мал.16.), обмеженої

графіком функції

2

x

ey

−

=

(крива Гаусса) і

віссю Ох.

х

у

О

Мал.16

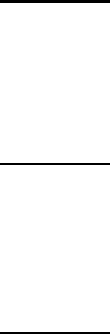
354

Розділ 7. ЗВИЧАЙНІ ДИФЕРЕНЦІАЛЬНІ РІВНЯННЯ

При розв’язанні багатьох задач математики, техніки, економі-

ки та інших галузей науки буває важко встановити закон, який

зв’язує шукані і відомі змінні величини. Але вдається встановити

зв’язок між похідними або диференціалами цих змінних, який ви-

ражається рівняннями або системами рівнянь. Такі рівняння нази-

вають диференціальними рівняннями. Термін “диференціальне

рів-

няння” введений у 1676 році Г.В.Лейбніцем.

Ми розглянемо тільки рівняння з функціями однієї змінної і

звичайними похідними, які називають звичайними диференціаль-

ними рівняннями

.

§ 1. Основні поняття про диференціальні рівняння

Означення. Диференціальним рівнянням називається рів-

няння, яке зв’язує незалежну змінну x, шукану функцію y=f(x) і її

похідні або диференціали різних порядків, тобто рівняння

0)y'...,'y,'y,y,x(F

)n(

= . (7.1)

Важливо зрозуміти, що шукана функція у диференціальному

рівнянні входить під знак диференціала або під знак похідної.

Означення. Порядком диференціального рівняння назива-

ється найвищий порядок похідної від невідомої функції, яка вхо-

дить у диференціальне рівняння.

Так, рівняння

05xy2y

2

=+−

′

є диференціальним рівнянням

першого порядку, а рівняння

0xsinyy2y =−−

′

+

′′

- диференціаль-

ним рівнянням другого порядку.

Означення. Розв’язком диференціального рівняння (7.1) на-

зивається така функція )x(y

ϕ

= , яка при підстановці у рів-

няння (7.1) перетворює його в тотожність.

Наприклад, для диференціального рівняння

0x2y =−

′

(7.2)

розв’язком є функція

2

xy = . Знайдемо похідну x2y =

′

і підстави-

мо у рівняння, одержимо:

.00;0x2x2 ≡=−

Слід зауважити, що y=x

2

не єдиний розв’язок рівняння. Це

рівняння має нескінчену множину розв’язків, які можна записати

так: y=x

2

+C.

355

§ 2. Диференціальні рівняння першого порядку

Означення. Диференціальним рівнянням першого порядку

називається рівняння, яке зв’язує незалежну змінну x , шукану

функцію y=f(x) і її першу похідну:

F(x,y,y′)=0. (7.3)

Оскільки похідну можна записати у вигляді відношення ди-

ференціалів, то в рівняння похідна може не входити, а будуть вхо-

дити диференціали невідомої функції і незалежної змінної.

Якщо рівняння (7.2) розв’язати відносно у′, то воно матиме

вигляд :

)y,x(fy =

′

або

)y,x(f

dx

dy

=

. (7.4)

Прості приклади показують, що диференціальне рівняння

може мати нескінчену множину розв’язків. Це ми бачимо на прик-

ладі рівняння (7.2). Легко переконатись також , що диференціальне

рівняння

x

y

y =

′

має розв’язками функції Cxy = , а диференціальне

рівняння

x

y

y −=

′

функції

x

C

y =

, де C - довільне число.

Як бачимо, в розв’язок наведених диференціальних рівнянь

входить довільне число

C . Надаючи сталій C різних значень, бу-

демо одержувати різні розв’язки диференціального рівняння.

Означення. Загальним розв’язком диференціального рівнян-

ня (7.3) називається функція

у=φ(х,С), (7.5)

яка залежить від однієї довільної сталої і задовольняє диферен-

ціальне рівняння при довільному значенні C .

Якщо функція (7.5) виражається неявно, тобто у вигляді

Ф(х,у,С)=0, (7.6)

то (7.6) називається загальним інтегралом диференціального

рівняння.

Означення. Частинним розв’язком диференціального рів-

няння (7.3) називається такий розв’язок , який одержується із

загального розв’язку (7.5) при деякому конкретному значенні

сталої C.

Ф(х,у,С

0

) називається частинним інтегралом диференціа-

льного рівняння.

356

На практиці при розв’язанні конкретних задач часто дово-

диться знаходити не всі розв’язки, а розв’язок, який задовольняє

певним початковим умовам. Однією із таких задач є задача Коші,

яка для диференціального рівняння першого порядку формулюєть-

ся так : серед усіх розв’язків диференціального рівняння (7.3)

знайти такий розв’язок

y

, який при заданому значенні незалежної

змінної

0

xx = дорівнює заданому значенню

0

y , тобто

00

y)x(y = або

0

xx

yy

0

=

. (7.7)

Умова (7.7) називається початковою умовою розв’язку.

Покажемо на прикладі, як знайти частинний розв’язок дифе-

ренціального рівняння, коли відомий загальний розв’язок і задана

початкова умова.

Ми бачимо, що диференціальне рівняння

x

y

y =

′

має загаль-

ний розв’язок

Cxy =

. Задамо початкову умову 6y

2x

=

. Підста-

вимо ці значення в загальний розв’язок, одержимо

С26 = , звідки

3С = . Отже, функція x3y = задовольняє і диференціальне рів-

няння і початкову умову.

Відповідь на питання про те, за яких умов рівняння (7.4) має

розв’язок, дає теорема Коші.

ТЕОРЕМА

( про існування та єдиність розв’язку). Якщо

функція

)y,x(f

і її частинна похідна )y,x(f

y

′

визначені і не-

перервні в області G , яка містить точку )y;x(M

000

, то існує

єдиний розв’язок )x(y

ϕ

= рівняння (7.4), який задовольняє

початковій умові :

00

y)x(y = .

Теорема Коші дає достатні умови існування єдиного

розв’язку диференціального рівняння (7.4). Зауважимо, що в умові

теореми не вимагається існування частинної похідної

)y,x(f

x

′

.

Графік довільного частинного розв’язку диференціального

рівняння називається інтегральною кривою. Загальному розв’язку

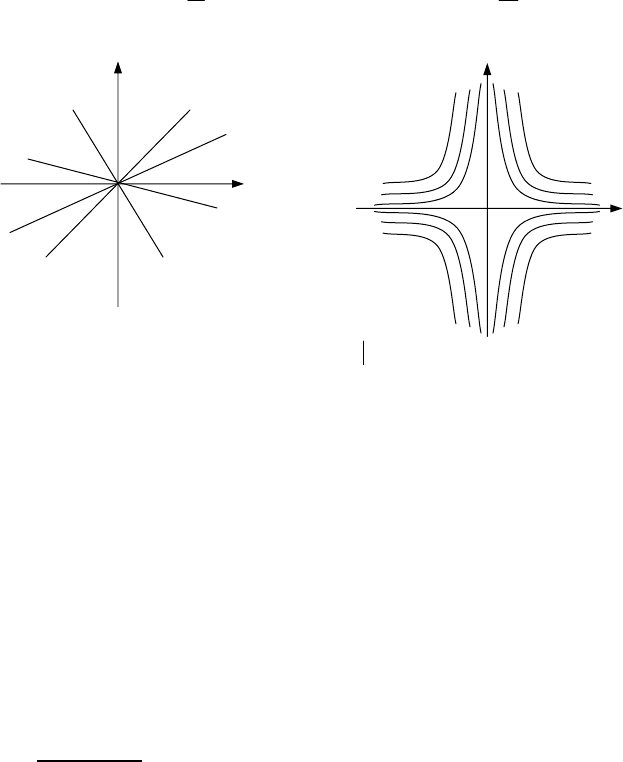
відповідає сім’я кривих. Так ми перевірили, що рівняння

x

y

y =

′

має загальний розв’язок

Cxy = , то йому відповідає сім’я прямих,

які проходять через початок координат (мал. 1).

357

Рівняння

x

y

y −=

′

має загальний розв’язок

x

C

y =

. Йому від-

повідає сім’я рівносторонніх гіпербол (мал.2).

Якщо задана початкова умова

0

xx

yy

0

=

, то це означає, що

задана точка

)y;x(M

000

через яку повинна проходити інтегральна

крива, яка відповідає шуканому частинному розв’язку. Таким чи-

ном, відшукання частинного розв’язку диференціального рівняння

за заданою початковою умовою геометрично означає, що із сім’ї

інтегральних кривих ми вибираємо ту, що проходить через точку

)y;x(M

000

.

Треба зауважити, що знаходження розв’язку диференціально-

го рівняння часто називають інтегруванням рівняння. При цьому

операцію інтегрування функцій називають квадратурою.

Загального методу розв’язування диференціальних рівнянь

першого порядку не існує. Розглянемо деякі методи розв’язування

окремих типів диференціальних рівнянь.

2.1. Диференціальні рівняння з відокремленими змінними

Означення. Рівняння вигляду

f

1

(y)dy=f

2

(x)dx, (7.8)

де f

1

(y) і f

2

(x) - задані функції, називається диференціальним рі-

внянням з відокремленими змінними.

В цьому рівнянні кожна із змінних знаходиться тільки в тій

частині рівняння, де знаходиться її диференціал. Рівняння

dx)x(fdy = є частинним випадком рівняння (7.8). Щоб розв’язати

рівняння (7.8), треба проінтегрувати обидві його частини:

x

y

0

Мал

.2

0

Мал

.1

x

y

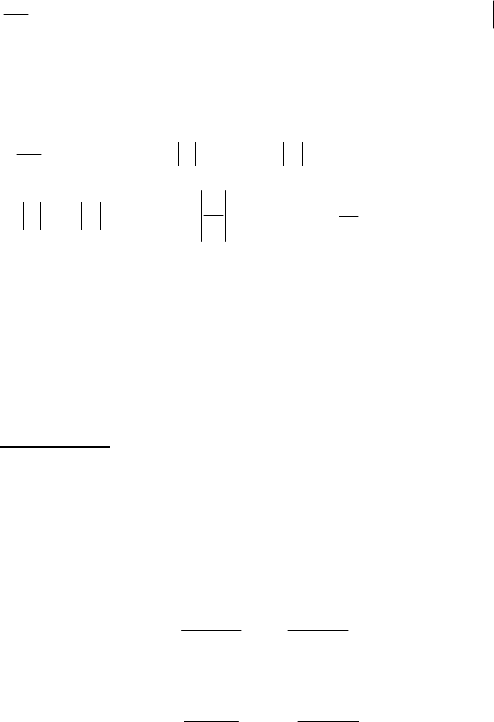
358

∫∫

+= Cdx)x(fdy)y(f

21

.

Зрозуміло, що довільну сталу С можна записувати в будь-якій

частині рівності.

Приклад

1. Розв’язати диференціальне рівняння:

dxx3

y

dy

2

=

, яке задовольняє початковій умові

.2y

0x

=

Розв’язування. Проінтегруємо ліву і праву частину рівняння,

причому для зручності потенціювання довільну сталу запишемо у

вигляді ln

|C| одержимо:

∫∫

= dxx3

y

dy

2

; Clnxyln

3

+= ;

3

xClnyln =− ;

3

x

C

y

ln =

;

3

x

e

С

y

=

;

3

x

Cey = - це загальний розв’язок диференціального рівняння.

Підставляючи в загальний розв’язок початкову умову, знай-

демо С

: С2 = .

Отже,

3

x

e2y = є частинним розв’язком даного рівняння.

2.2.

Диференціальні рівняння з відокремлюваними змінними

Означення. Рівняння вигляду

f

1

(x) f

2

(y)+g

1

(x) g

2

(y)=0 (7.9)

називається диференціальним рівнянням з відокремлюваними

змінними.

В цьому рівнянні змінні ще не відокремлені, але, поділивши

обидві частини рівняння на добуток f

2

(y)g

1

(x) , одержимо

рівняння з відокремленими змінними:

0dy

)y(f

)y(g

dx

)x(g

)x(f

2

1

=+

.

Інтегруючи це рівняння, запишемо

Cdy

)y(f

)y(g

2

dx

)x(

1

g

)x(

1

f

=+

∫

.

Одержали загальний інтеграл даного рівняння.

Приклад

2. Розв’язати диференціальне рівняння

x(y+1)dx-(x

2

+1)ydy=0.

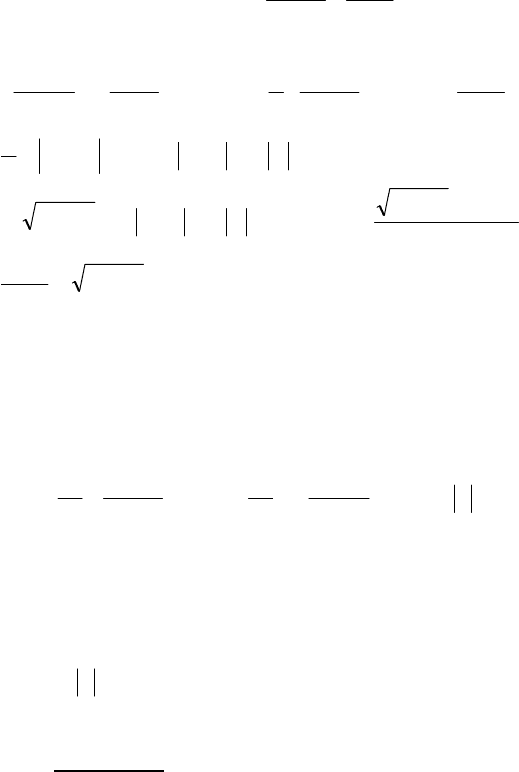
359

Розв’язування. Поділимо обидві частини цього рівняння на

)1x)(1y(

2

++ , після чого одержимо

0

1y

ydy

1x

xdx

2

=

+

−

+

.

Інтегруючи, будемо мати

;

1y

ydy

1x

xdx

2

∫∫

+

=

+

;dy

1y

1

1dx

1x

x2

2

1

2

∫∫

⎟

⎠

⎞

⎜

⎝

⎛

+

−=

+

;Cln1ylny1xln

2

1

2

++−=+

;yCln1yln1xln

2

=−+++

()

;

C

1y1x

lny

2

+⋅+

=

1x

1y

Ce

2

y

+=

+

- загальний інтеграл диференціального рівняння.

Приклад 2. Знайти частинний розв’язок диференціального рі-

вняння

()

0ydxdyx1

2

=++ , який задовольняє початкову умову

.1)0(y =

Розв’язування. Відокремимо змінні, поділивши рівняння на

)x1(y

2

+⋅ , і проінтегруємо дане рівняння:

;0

x1

dx

y

dy

2

=

+

∫∫

=

+

+ ;C

x1

dx

y

dy

2

Carctgxyln =+

.

Одержали загальний інтеграл диференціального рівняння.

Використовуючи початкову умову, знайдемо довільну сталу С:

,C0arctg1ln =+ звідки

0C =

.

Знайдену сталу підставимо у загальний інтеграл і відшукаємо

частинний розв’язок:

;0arctgxyln =+ звідки .ey

arctgx−

=

2.3.Однорідні диференціальні рівняння

Означення. Функція двох змінних f(x,y) називається одно-

рідною

n

- го виміру, якщо виконується умова

)y,x(ft)ty,tx(f)y,x(f

n

== .

Наприклад,

22

yx)y,x(f += , )yx(ft)ty,tx(f

222

+= - од-

норідна функція другого виміру.

360

Означення. Диференціальне рівняння

)y,x(fy =

′

(7.10)

називається однорідним, якщо функція f(x,y) однорідна нульового

виміру.

Покажемо, що це рівняння можна звести до рівняння з відо-

кремленими змінними.

Розглянемо функцію

).ty,tx(f Зробимо заміну

x

1

t =

, будемо

мати:

.

x

y

x

y

,1f)ty,tx(f

⎟

⎠

⎞

⎜

⎝

⎛

ϕ=

⎟

⎠

⎞

⎜

⎝

⎛

= Тоді рівняння (7.10) запишеться у

вигляді

⎟

⎠

⎞

⎜

⎝

⎛

ϕ=

′

x

y

. (7.11)

В загальному випадку змінні в однорідному рівнянні не відо-

кремлюються зразу. Але, якщо ввести допоміжну невідому функ-

цію u=u(x) за формулою

u

x

y

= або

xu

y

= , (7.12)

то ми зможемо перетворити однорідне рівняння в рівняння з відо-

кремлюваними змінними.

З формули (7.12) знайдемо

uxuy

′

+=

′

і рівняння

⎟

⎠

⎞

⎜

⎝

⎛

ϕ=

′

x

у

y набуде вигляду: u+xu′=φ(u),

тобто

u)u(

dx

du

x −ϕ=⋅

, звідки

x

dx

u)u(

du

=

−ϕ

.

Після інтегрування одержимо Cxln

u)u(

du

+=

−ϕ

∫

.

Звідси знаходимо вираз для функції u, вертаємось до змінної

y=xu і одержимо розв’язок однорідного рівняння.

Найчастіше не вдається знайти функцію u явно вираженою,

тоді, після інтегрування, в ліву частину слід підставити

x

y

замість u .

В результаті отримаємо розв’язок рівняння в неявному вигляді.

Приклад

1. Знайти розв’язок однорідного рівняння

xy2x

yxy

y

2

−

=

′

.

Шинкарик М.І. Вища математика

Подождите немного. Документ загружается.