Шинкарик М.І. Вища математика
Подождите немного. Документ загружается.


11
.0
a...aa
............
a...aa
............
a...aa
............
a...aa
a...aa
nn2n1n
in2i1i
in2i1i
n22221
n11211
=
λλλ
48)91636184(8
431
312
321
42
431
1248
642
−=−−+−+=
−
−
−
⋅⋅=
−
−
−
елементів, в т.ч. з розглянутого i -го рядка, то λ можна винести з
цієї суми за дужки. Якщо записати вираз в дужках у вигляді визнач-
ника, то одержимо попередню рівність.
Наслідок. Якщо довільний рядок (або стовпець) визначника
помножити на число λ, то величина визначника зміниться в λ раз.
Зокрема, якщо елементи, наприклад, першого рядка визначни-
ка другого порядку мають спільний
множник “
λ
”, то
.
aa
aa
)aaaa(aaaa
aa
aa
2221
1211
2112221121122211
2221
1211
λ=−λ=λ−λ=
λλ
Приклад
4. У визначнику третього порядку
4872128244814432
431
1248
642
−=−−+−+=
−
−
−
елементи першого і другого рядків мають спільні множники “2” і
“4”, тому їх можна винести за знак визначника
Властивість 6. Якщо у визначнику елементи одного рядка
(або стовпця) пропорційні відповідним елементам іншого рядка (або
стовпця), то визначник дорівнює нулю:
Доведення. Нехай елементи
i -го і k -го рядків пропорційні. За
властивістю 5 постійний множник пропорційності λ можна винести
за знак визначника. При цьому одержимо добуток числа λ на ви-
значник з двома однаковими рядками, який дорівнює нулю (за
властивістю 4).
12
Приклад 5. Визначник третього порядку
,03630003630
540
963
321
=−++−+−=−
−
тому що перший і другий рядки пропорційні.
Властивість 7. Якщо у визначнику всі елементи довільного
рядка ( або стовпця) є сумою двох доданків, то визначник можна
представити у вигляді суми двох визначників. При цьому елементи
розглянутого рядка ( або стовпця ) в першому визначнику є перши-
ми доданками, а елементи відповідного рядка ( або стовпця)
другого
визначника - другими доданками:
+=
+++
nn2n1n
in2i1i
n22221
n11211
nn2n1n
inin2i2i1i1i
n22221
n11211
a...aa
............
a...aa
............
a...aa
a...aa
a...aa
............
ba...baba
............
a...aa
a...aa
.
a...aa
............
b...bb
............
a...aa
a...aa
nn2n1n
in2i1i
n22221
n11211
Доведення. Доведемо справедливість цієї властивості на
прикладі визначника другого порядку:
.
aa
bb
aa
aa
)abab()aaaa(
a)ba(a)ba(
aa
baba
2221
1211
2221
1211
2112221121122211
211212221111
2221
12121111
+=−+−=
=+−+=
++
Приклад 6
. Обчислити визначник:
.5191600430
210
354
123
−=−−+++−=
−
−
−
Елементи, наприклад, другого рядка можна представити у ви-
гляді суми двох доданків:
=
−
−
−
+
−
−
−
=
−
++−−
−
=
−
−
−
210
122
123
210
232
123
210
122322
123
210
354
123
13
.512130)3800212()6800218( −=−−=−−+++−+−−+++−=
Властивість 8. Величина визначника не зміниться, якщо до
елементів довільного рядка (або стовпця) додати відповідні елемен-
ти іншого рядка (або стовпця), помножені на одне і те ж число λ:
.
a...aa
............
а...аа
............
aa...aaaa
............
a...aa
a...aa
a...aa
............
a...aa
............
a...aa
............
a...aa
a...aa
nn2n1n
кn2к1к
knin2k2i1k1i
n22221
n11211
nn2n1n
kn2k1k
in2i1i
n22221
n11211
λ+λ+λ+
=
Доведення. Для доведення представимо визначник правої час-
тини згідно з властивістю 7 у вигляді суми двох визначників:
.
a...aa
............
a...aa
............
a...aa
............
a...aa
a...aa
a...aa
............
a...aa
............
a...aa
............
a...aa
a...aa
a...aa
............
a...aa
............
aa...aaaa
............
a...aa
a...aa
nn2n1n
kn2k1k
kn2k1k
n222
n11211
nn2n1n
kn2k1k
іn2i1i
n22221
n11211
nn2n1n
kn2k1k
kn1i2k1i1k1i
n22221
n11211
21
λλλ
+
+=
λ+λ+λ+
В другому визначнику правої частини елементи і-го рядка пропор-
ційні відповідним елементам
k-го рядка, тому за властивістю 6 та-
кий визначник дорівнює нулю. Отже, має місце властивість 8.
14
Приклад 7
. Обчислити визначник
.11
170
140
231
)3(25)3)(3(2)3(13
140
231
523
140
231
−=
−
−
=
=
−+−−+−−⋅+
−
=
−
−
Тут ми до елементів третього рядка додали відповідні елемен-
ти першого рядка, помножені на число “-3”.
Надалі, властивість 8 використовується для обчислення ви-
значників вищих порядків. При цьому в довільному рядку ( або сто-
впці) утворюємо всі нулі, крім одного елемента.
Нехай маємо визначник −
n
го порядку (
)3n >
;
nnnj2n1n
inij2i1i
n2j22221
n1j11211
a...a...aa
..................
a...a...aa
..................
a...a...aa
a...a...aa
=Δ
.
Означення
1. Мінором
ij
M
елемента
ij
a
визначника
−
n
го
порядку називається визначник −− )1n( го порядку, одержаний
із попереднього після викреслювання −i го рядка і
−j
го стовпця,
на перетині яких знаходиться даний елемент.
Означення 2. Алгебраїчним доповненням
ij
A елемента
ij
a
визначника −
n
го порядку називається мінор для цього елемента,
взятий із знаком “+”, якщо число
)ji( +
- парне та із знаком “-”,
якщо воно непарне. Тобто
ij
ji
ij
M)1(A
+
−= .
Приклад 8. Знайти алгебраїчні доповнення до елементів
13
a
та
32
a визначника
215
306
124
−
−
.
Алгебраїчні доповнення
A
13
і A
32
знайдемо за попередньою
формулою:
1313
31
13
МM)1(A =−=
+
; .MM)1(A
3232
23
32
−=−=
+

15
Згідно з означенням 1 маємо:
,65016
15
06
215
306
124
M
13
=⋅−⋅==
−
−
=
.186126)1(34
36
14
215
306
124
M
32
=+=⋅−−⋅=
−
=
−
−
=
Шукані алгебраїчні доповнення будуть
.18A;6A
3213
−==
Властивість 9. (Теорема Лапласа).
Визначник дорівнює сумі добутків елементів довільного
рядка (або стовпця) на відповідні алгебраїчні доповнення:
);n,...,2,1i(AaAa...AaAa
n
1j
ijijinin2i2i1i1i
==+++=Δ
∑
=
).n,...,2,1j(AaAa...AaAa
n
1i
ijijnjnjj2j2j1j1
==+++=Δ
∑
=
Ця теорема називається ще теоремою розкладу. При цьому
перша формула є розкладом визначника за елементами його рядка, а
друга - розкладом визначника за елементами його стовпця.
Доведення. Доведемо цю властивість для визначника третього
порядку:
).aaaa(a
)aaaa(a)aaaa(aaaaaaa
aaaaaaaaaaaa
aaa
aaa
aaa
3122322113
33213123123223332211113223332112
312213133221312312332211
333231
232221
131211
−+
+−+−=−−
−−++==Δ
Однак,
,A
aa
aa
aaaa
11
3332
2322
32233322
==−
,A
aa
aa
)aaaa(aaaa
12
3332
2321
3123332133213123
=−=−−=−
.A
aa
aa
aaaa
13
3231
2221
31223221
==−
Таким чином,
.AaAaAa
131312121111
++=Δ
(1.1)
16
Це формула розкладу визначника за елементами першого ряд-
ка. Аналогічно можна знайти розклад визначника за елементами
іншого рядка або довільного стовпця.
З допомогою цієї властивості, обчислення визначника
−
n
го
порядку зводиться до обчислення визначників
)1n( −
- го порядку.
Тому при обчисленні таких визначників найкраще вибирати для ро-
зкладу рядок або стовпець, в якому є нулі. При цьому будемо обчи-
слювати не
n
визначників
)1n( −
- го порядку, а менше.
Приклад 9. Обчислити визначник 3-го порядку , розклавши
його за елементами першого рядка:
.53694024)518()1(3)200()1(2)240()1(1
65
13
)1()3(
05
43
)1(2
06
41
)1(1
065
413
321
432
312111
−=−+−=+−⋅−−−⋅+−−⋅
=
−
−⋅−+−⋅+
−
−⋅=−
−
+++
Зауваження. Даний визначник простіше було б обчислювати,
розклавши його за елементами третього рядка (або третього сто-
впця), оскільки один із доданків не потрібно обчислювати (елемент
0a
33
=
).
.531669
)106(4)518(3
65
21
)1(4
65
13
)1(3
065
413
321
54
−=+−=
=−−+−=−⋅+
−
−⋅−=−
−
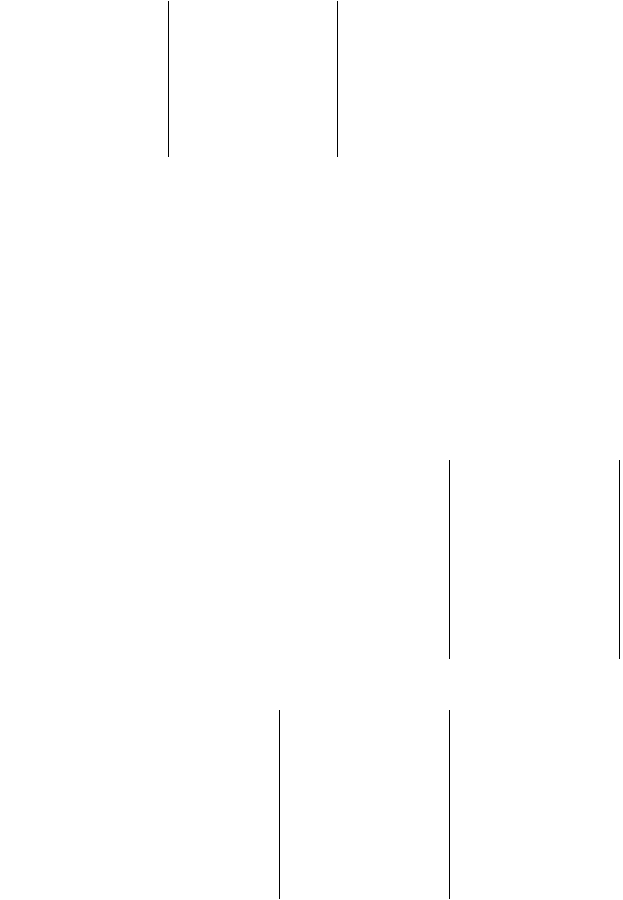
Наслідок 1 (Теорема заміщення).
Нехай
in2i1i
A,...,A,A - алгебраїчні доповнення елементів i -го
рядка визначника
−
n
го порядку .
a...aa
............
a...aa
............
a...aa
a...aa
nn2n1n
in2i1i
n22221
n11211
=Δ
Тоді сума добутків алгебраїчних доповнень елементів і-го
рядка на довільні числа
b
1
, b
2
,…, b
n
дорівнює такому визначнику
−
n
го порядку Δ
′
, в якого елементами
i
-го рядка є числа b
1
,
b
2
,…, b
n
, а інші - співпадають з відповідними елементами визна-
чника
Δ.
17
=+++
kn
in
2
k
2
i
1
k
1
i
Aa...AaAa
Доведення. За теоремою маємо, що
Δ
′
=+++
inn2i21i1
Ab...AbAb .
Тут
,Ab...AbAb
a...aa
............
b...bb
............
a...aa
a...aa
inn2i21i1
nn2n1n
n21
n22221
n11211
+++==Δ
′
де права частина одержалась після розкладу визначника
−
n
го по-
рядку за елементами
i -го рядка. Це і доводить теорему.
Аналогічно, сума добутків алгебраїчних доповнень елементів
−j
го стовпця на довільні числа
n21
b,...,b,b
, тобто
,Ab...AbAb
njnj22j11
+++ дорівнює визначнику
Δ
′
, елементами
−j го стовпця якого є числа
n21
b,...,b,b , а інші елементи
співпадають з відповідними елементами визначника
Δ .
Наслідок 2
(Теорема анулювання).
Сума добутків елементів довільного рядка (або стовпця)
на алгебраїчні доповнення паралельного іншого рядка (або сто-
впця) дорівнює нулю.
Доведення. У визначнику
Δ
виділимо два рядки
i -ий і k -ий.
Знайдемо суму добутків елементів
i -го рядка на алгебраїчні доповнення
елементів
k
-го рядка:
.Aa...AaAa
knin2k2i1k1i
+++
За теоремою заміщення цю суму мо-
жна замінити визначником з двома однако-
вими рядками
.
a...aa
............
a...aa
............
a...aa
............
a...aa
a...aa
nn2n1n
in2i1i
in2i1i
n22221
n11211
nn2n1n
kn2k1k
in2i1i
n22221
n11211
a...aa
............
a...aa
............
a...aa
............
a...aa
a...aa
=Δ

18
Одержаний визначник має два однакові рядки, а тому
дорівнює нулю.
Приклад 10. Користуючись властивостями визначників, об-
числити
.
235
123
211
−−
−
=Δ
Розв’язування. Додамо елементи першого і другого стовпців, а
від елементів третього стовпця віднімемо подвоєні елементи першо-
го. Одержимо:
.50)16(10
61
11
251
122
55
)1(1
1225
553
001
2
−=+−=
−
−
⋅⋅=
−
−
−⋅=
−
−=Δ
Приклад 11. Обчислити визначник, використавши його вла-
стивості:
.
71140
282156
5416
−=Δ
Розв’язування. Винесемо за знак визначника спільний множ-
ник “8” першого стовпця і спільний множник “7” другого рядка
.
7115
431
542
78 −⋅⋅=Δ
Віднімемо від елементів першого рядка подвоєні відповідні
елементи другого рядка. До елементів третього рядка додамо відпо-
відні елементи другого рядка, помножені на число “-5”
.
2740
431
1320
78
−
−
−
⋅⋅=Δ
Такий визначник легко обчислити, розклавши його за елемен-
тами першого стовпця:
.112)5254(56
274
132
)1(178
3
=+−−=
−
−
−⋅⋅⋅=Δ
§ 3. Обчислення визначників довільного порядку
Визначником
n
-го порядку називається число, яке дорівнює
сумі добутків елементів довільного рядка або стовпця, на відповідні
алгебраїчні доповнення.
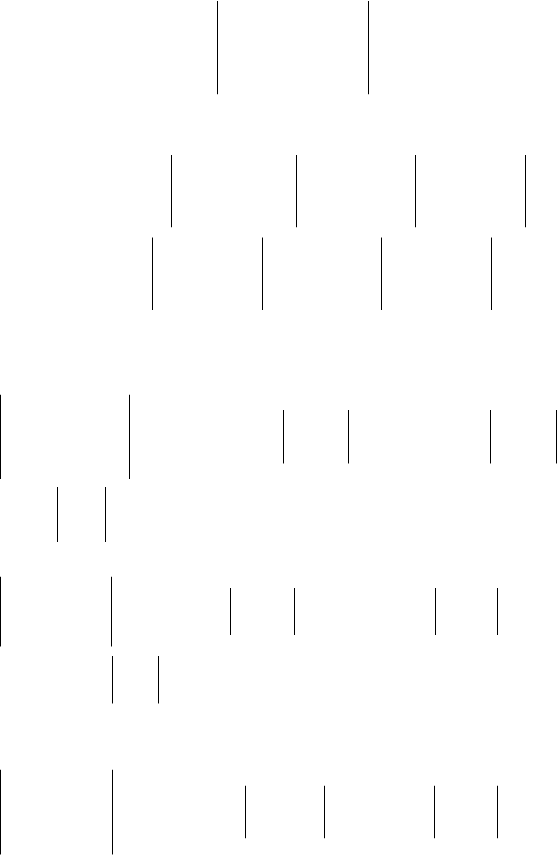
19
При цьому мають місце формули розкладу визначника за еле-
ментами його довільного рядка (або стовпця) (1.1).
Означення визначника
n
-го порядку взято за метод його об-
числення.
Приклад 1. Обчислити визначник 4-го порядку:
.
5021
0113
2101
4321
−
−−
Розв’язування.Розкладемо визначник за елементами другого
рядка:
.
021
113
321
)1(2
521
013
421
)1(1
501
013
431
)1(0
502
011
432
)1(1
4232
2212
−−−⋅+
−
−−⋅+
+
−
−−⋅+
−
−−−⋅=Δ
++
++
Кожен із цих визначників обчислимо, ще раз використавши
формулу Лапласа. Перший та третій визначники розкладемо за еле-
ментами другого рядка:
+
−
−−+
−
−⋅−=
−
−−
++
52
42
)1)(1(
50
43
)1()1(
502
011
432
2212
+−−⋅−⋅−−−⋅−⋅−=−⋅+
+
)810()1(1)015()1()1(
02
32
)1(0
4332
;318150 =+−=+
.63)9(1)18(30
)45()1(1)810()1(3
21
21
)1(0
51
41
)1)(1(
52
42
)1(3
521
013
421
4332
2212
=−−−−=+
+−−⋅−⋅−−−⋅−⋅=−⋅+
+
−
−−+
−
−⋅=
−
−
+
++
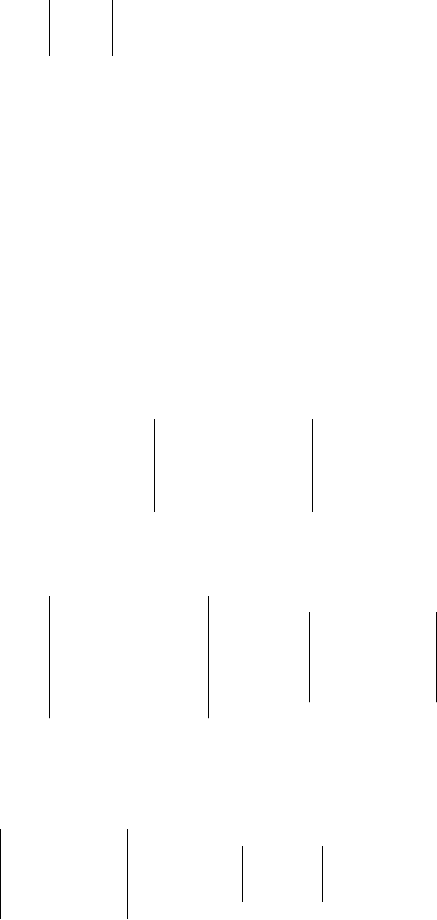
Четвертий визначник розкладемо за елементами третього рядка:
+
−
−+
−−
⋅−⋅=−−
++
13
31
)1(2
11
32
)1(1
021
113
321
2313
20
.21)10(210
)91()1(2)32()1(1
13
21
)1(0
5433
=−⋅−=+
+−−⋅−++−⋅−⋅=
−
−⋅+
+
Отже,
.244263321)1(263)1(13)1(1
653
−=+−−=⋅−⋅+⋅−⋅+⋅−⋅=Δ
Як бачимо, обчислення визначника 4-го порядку зводиться до
обчислення чотирьох визначників 3-го порядку, а обчислення ви-
значника 5-го порядку - до обчислення п’яти визначників 4-го по-
рядку або двадцяти визначників 3-го порядку. Тому доцільно споча-
тку перетворити визначник так, щоб в одному з рядків (або стовп-
ців) всі елементи, крім
одного, стали нульовими. Цього можна дося-
гти, використавши властивості визначників.
Таким чином, обчислення визначника
−
n
го порядку зводить-
ся до обчислення лише одного визначника
)1n( − -го порядку.
Приклад 2. Обчислити визначник, використавши його влас-
тивості:
.
5021
0113
2101
4321
−
−−
=Δ
Розв’язування
. Від елементів третього стовпця віднімемо від-
повідні елементи першого стовпця, а до елементів четвертого стовп-
ця додамо відповідні елементи першого стовпця, помножені на “-2”.
.
712
641
222
)1(1
7121
6413
0001
2221
3
−−
−−−−⋅=
−−
−−−
=Δ
Одержаний визначник 3-го порядку можна обчислити, на-
приклад, за правилом Саррюса, або звести до визначника 2-го по-
рядку, віднявши від елементів другого і третього стовпців
відповідні елементи першого стовпця
.24122))5()3(
)9()3((2
93
53
)1(2
932
531
002
2
−=⋅−=−⋅−−
−−⋅−⋅−=
−−
−−
−⋅−=
−−
−−−−=Δ
Одержали значно легшим шляхом той же результат визначника.
