Шинкарик М.І. Вища математика
Подождите немного. Документ загружается.

71
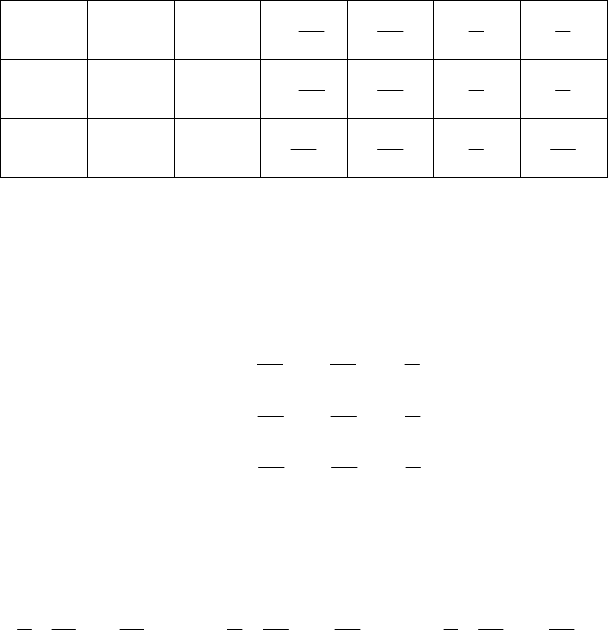
Таблиця
3. Помножимо елементи третього рядка на “-5” і “-2”
і додамо до відповідних елементів другого і першого рядків табл.2.
За ключовий елемент візьмемо число “-30” і поділимо на нього всі
елементи другого рядка і запишемо другим рядком таблиці 4.
Таблиця
4. Інші клітинки заповнимо аналогічно. Помножимо
елементи другого рядка на “-7” і “11” і додамо до відповідних
елементів третього і перших рядків таблиці 3.
Такі перетворення показано справа біля кожної з таблиць
(числа вказують, що даний рядок на нього треба перемножити, а
стрілки – до якого рядка потрібно додати відповідні елементи).
Якщо перші два рядки
табл.4 поміняти місцями, то по
головній діагоналі одержаної матриці-таблиці є три ненульові еле-
менти:
1 0 0
10
7
−
15
2
5
2
6
5
0 1 0
10
7
−
15
7
5
2
6
7
0 0 1
10
9
15
1
5
1
6
13
Це означає, що ранги основної і розширеної матриць однакові
і дорівнюють 3. Тобто вихідна система 3 лінійних рівнянь з 5 неві-
домими сумісна і має безліч розв’язків (ранг менший за кількість
невідомих).
Запишемо отриману систему базисних рівнянь, виходячи із
таблиці 4.
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
=++
=+−
=+−
.
5
1
x
15
1
x
10
9
x
,
5
2
x
15
7
x
10
7
x
,
5
2
x
15
2
x
10
7
x
543
542
541
Маємо три базисні невідомі
(х
1
, х
2
, х
3
) і дві вільні (х
4
, х
5
). Дру-
га таблиця виділяє базисну невідому
х
2
третя таблиця - х
3
і четверта
таблиця -
х
1
.
Звідси загальний розв’язок вихідної системи запишеться так:
,x
15
2
x
10
7
5
2
x
541
−+= ,x
15
7
x
10
7
5
2
x
542
−+=
543
x
15
1
x
10
9
5
1
x −−=
.

72
Для перевірки правильності знайдених розв’язків, достатньо
підставити ці значення
х
1
, х
2
, х
3
у задану систему лінійних рівнянь і
отримати тотожності.
Для одержання частинних розв’язків системи, надамо вільним
невідомим
х
4
, х
5
довільних значень. Наприклад, якщо х
4
=0, х
5
=0,
то:
.0x,0x,
5
1
x,
5
2
x,
5
2
x
54321
=====
Якщо
х
4
=1, х
5
= −1, то розв’язок буде такий:
1x,1x,
30
29
x,
30
47
x,
30
37
x
54321
−==−=== , і т.д.
Таких частинних розв’язків можна знайти безліч.
§14. Системи лінійних однорідних алгебраїчних рівнянь
Система
m лінійних алгебраїчних рівнянь з n невідомими на-
зивається однорідною, якщо вона має вигляд
⎪
⎪
⎩
⎪
⎪
⎨
⎧
=+++
=+++
=+++
.0xa...xaxa
..................................................
,0xa...xaxa
,0xa...xaxa
nmn22m11m
nn2222121
nn1212111
(1.8)
Вона одержується із системи лінійних алгебраїчних рівнянь
(1.3), якщо
.0b...bb
m21
==== Розширена матриця Ã цієї системи
одержується із основної матриці
А, якщо приєднати нульовий стов-
пець. Значить ранг матриці
А рівний рангу розширеної матриці Ã.
При цьому за теоремою Кронекера-Капеллі вихідна система завжди
сумісна.
Якщо ранг матриці
A
системи лінійних однорідних рівнянь
дорівнює кількості невідомих
)nr( =
, то система має єдиний нуль-
овий (тривіальний) розв’язок:
.0x...xx
n21
==== Це випливає з
теореми Крамера, оскільки всі визначники
j
Δ одержуються із ви-
значника
nn2n1n
n22221
n11211
a...aa
............
a...aa
a...aa
=Δ
(1.9)

73
заміною
j
-го стовпця стовпцем із вільних членів
,...,0b,0b
21
==
0b
n
= , а тому
.0
0
x...xx
n21
=
Δ
====
Значить, система
n
лінійних однорідних алгебраїчних рівнянь
з
n
невідомими має нульові розв’язки тільки тоді, коли визначник
системи , складеної із коефіцієнтів, які стоять біля невідомих від-
мінний від нуля.
Система
n
лінійних однорідних алгебраїчних рівнянь з
n
не-
відомими має ненульові розв’язки тільки тоді, коли визначник сис-
теми, складеної із коефіцієнтів, які стоять біля невідомих дорівнює
нулю
).0( =Δ Тобто , система має ненульові розв’язки тільки тоді,
коли
n
r
<
, де
r
- ранг матриці
А
, а
n
- число невідомих.
Приклад 1. Розв’язати систему лінійних однорідних рівнянь.
⎪
⎩
⎪
⎨
⎧
=++
=+−
=−+
.0xx2x3
,0x2x3x2
,0xxx
321
321
321
Розв
’язування. Так як кількість рівнянь )3m( = співпадає з
кількістю невідомих
)3n( = , а визначник
16249643
123
232
111
−=−−−+−=−
−
=Δ
системи відмінний від нуля, то задана система лінійних однорідних
рівнянь має тільки нульовий розв’язок:
.0xxx
321
===
Приклад 2. Розв’язати систему лінійних однорідних рівнянь
⎪
⎪
⎩
⎪
⎪
⎨
⎧
=++−+
=+−+
=++−+
=−+−+
.0xxx3x9x3
,0xx2x6x2
,0xxxx3x
,0xx4xx3x
54321
4321
54321
54321
Розв
’язування. Знайдемо ранг матриці, складеної з коефіціє-
нтів при невідомих. Для цього зведемо її до діагонального вигляду з
допомогою елементарних перетворень:

74
.
400
010
001
000
400
010
001
700
400
010
001
700
400
310
001
1110
710
310
001
211000
27000
23000
00001
411000
27000
23000
14131
113
93
01262
11131
14131
A
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
⇔
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
⇔
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
−
⇔
⇔
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
−
−
⇔
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
−
−
⇔
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
−
−
⇔
⇔
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
−
−
−−
⇔
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
−
−
−
=
Ранг останньої матриці, а значить, і еквівалентної їй матриці
A
дорівнює 3 ( )3r = і менший, ніж число невідомих, а тому
вихідна система має ненульові розв’язки. Візьмемо ті рівняння за-
даної системи, в яких коефіцієнти при невідомих утворюють базис-
ний мінор, наприклад:
,81281
012
111
141
М =−++−=
−
=
який відмінний від нуля.
Задана система лінійних рівнянь еквівалентна такій:
⎪
⎩
⎪
⎨
⎧
+−=+
+−=++
+−=−+
.x2x6xx2
,xx3xxx
,xx3xx4x
3241
32541
32541
Розв’яжемо її, відносно невідомих
541
x,x,x , методом Гаусса.
Виключимо
1
x в другому і третьому рівняннях
⎪
⎩
⎪
⎨
⎧
=+−
=+
+−=−+
.0x2x7
,0x2x3
,xx3xx4x
54
54
32541
Виключимо
4
x в третьому рівнянні

75
⎪
⎪
⎩
⎪
⎪
⎨
⎧
=−
=+
+−=−+
.0x
3
8
,0x2x3
,xx3xx4x
5
54
32541
Із останнього рівняння знаходимо, що
0x
5
=
, а значить, і
0x
4
=
(із
другого рівняння). З першого рівняння одержимо
.xx3x
321
+−=
Таким чином,
;xx3x
321
+−= .0xx
54
==
При довільних значеннях вільних невідомих
2
x та
3
x одер-
жимо відповідні значення базисних невідомих. Наприклад, один із
часткових розв’язків такий:
.0x;0x;1x;1x;2x
54321
====−=
ТЕОРЕМА. Якщо визначник
Δ
(1.9) системи
n
лінійних
однорідних алгебраїчних рівнянь з
n
невідомими дорівнює ну-
лю, а серед алгебраїчних доповнень
А
ij
(
;n,...,2,1і =
)n,...,2,1j=
елементів
−i
го рядка є ненульові, то ця система має ненульо-
вий розв’язок:
x
j
=А
ij
·t. (1.10)
Тут
t- деякий параметр.
Доведення
. Підставивши розв’язок (1.10) в систему рівнянь
(1.8) при
n
m
=
, одержимо:
,0t0t)Aa...AaAa(xa...xaxa
inkn2i2k1i1knkn22k11k
=⋅=+++=+++
при
ik ≠ (за теоремою анулювання);
,0tt)Aa...AaAa(xa...xaxa
inin2i2i1i1inkn22k11k
=⋅Δ=+++=+++
при
ik = (за умовою теореми).
Приклад 3. Розв’язати систему лінійних однорідних рівнянь
⎪
⎩
⎪
⎨
⎧
=++
=++
=++
.0x3x4x
,0x5x6x3
,0xxx
321
321
321
Розв
'язування. Визначник
.0209651218
341
563
111
=−−−++==Δ
Знайдемо алгебраїчні доповнення до елементів, наприклад,
першого рядка:
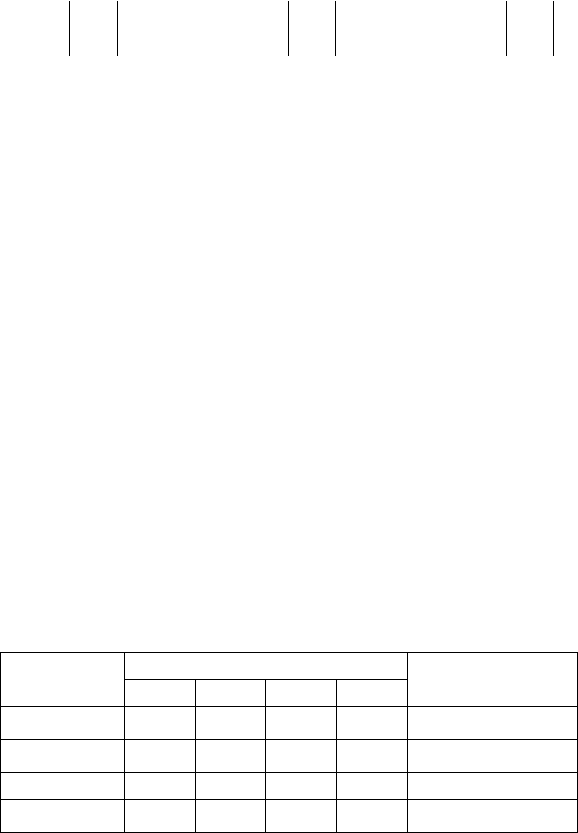
76
,2
34
56
)1(A
2
11
−=−= ,4
31
53
)1(A
3
12
−=−= .6
41
63
)1(A
4
13
=−=
Задана система лінійних однорідних алгебраїчних рівнянь має
розв’язок
,t6x;t4x;t2x
321
=−=−= який залежить від параметра
.
t
§15. Деякі економічні задачі
◙ Задача міжгалузевого балансу
В деяких задачах макроекономіки ставиться питання про ефе-
ктивне ведення багатогалузевого господарства. Тут кожна галузь є і
виробником , і споживачем деякої продукції (як своєї, так і продук-
ції, виробленої іншими галузями).
Однак, з економічної точки зору, міжгалузевий баланс є більш
ефективним у вартісному виразі. При цьому об’єднання
окремих
галузей у підгрупи полегшує складання балансів продукції.
Введемо такі позначення:
x
i
- загальна вартість продукції, виробленої в і-ій галузі (план вало-
вого випуску продукції)
(i=1,2,…,n);
ij
x
- вартість продукції
−i
ої галузі, необхідної для випуску
продукції
−j го підрозділу ( )n,...,2,1j = ;
i
y
- вартість продукції −i ої галузі, призначеної для реалізації (кін-
цевий продукт).
Прямі витрати одиниць
−i ої галузі, які використовуються
для випуску одиниці виробу продукції
−j
ої галузі, а також кінце-
вий продукт задані таблицею:
Вартість
продукції
Прямі витрати Кінцевий
продукт
1 2 …
n
1
x
11
x
12
x
… X
1n
1
y
2
x
21
x
22
x
…
X
2n
2
y
… … … … … …
n
x
x
n1
x
n2
… x
nn
n
y
Зв’язок між цими величинами запишемо у вигляді системи рі-
внянь:
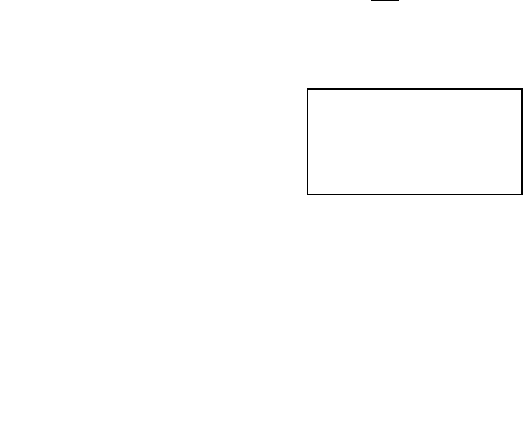
77
⎪
⎪
⎩
⎪
⎪
⎨
⎧
++++=
++++=
++++=
.yx...xxx
.............................................
,yx...xxx
,yx...xxx
nnn2n1nn
2n222212
1n112111
Рівняння цієї системи називаються балансовими.
Позначимо
ij
a - вартість продукції −i ої галузі , необхідної
для випуску одиниці продукції
−j ої галузі:
j
ij
ij
x
x
a =
.
Матриця, складена із величин
ij
a
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
nn2n1n
n22221
n11211
a...aa
............
a...aa
a...aa
A
а її елементи – коефіцієнтами прямих витрат.
Враховуючи, що
jijij
xax =
, вихідна система запишеться так:
⎪
⎪
⎩
⎪
⎪
⎨
⎧
++++=
++++=
++++=
,yxa...xaxax
........................................................
,yxa...xaxax
,yxa...xaxax
nnnn22n11nn
2nn22221212
1nn22121111
⎪
⎪
⎩
⎪
⎪
⎨
⎧
=+++−
=+++−
=+++−
.y)xa...xaxa(x
........................................................
,y)xa...xaxa(x
,y)xa...xaxa(x
nnnn22n11nn
2nn22221212
1nn22121111
Позначимо через
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
n
2
1
x
...
x
x
X
і назвемо вектор-планом
,X
а
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
n
2
1
y
...
y
y
Y
і назвемо
вектором кінцевих продуктів
Y
.
називається
матрицею прямих
витрат,
або

78
Попередня система запишеться у вигляді матричного рівняння
Y
AX
X
=− , або
Y
AX
EX
=− , звідси YX)AE( =− ,
де
E
- одинична матриця.
Позначимо
B
A
E
=− , тоді система лінійних алгебраїчних
рівнянь запишеться так
.YBX =
Помножимо з лівого боку обидві частини рівняння на
1
B
−
:
Y
B
BX
B
11 −−
= . Звідси
Y
B
X
1−
= .
Тобто вектор-план
X
можна знайти, помноживши
1
B
−
на
вектор кінцевих продуктів.
Матриця
1
B
−
називається матрицею повних витрат. Елемен-
ти цієї матриці включають прямі і непрямі витрати.
Задача 1. Прямі витрати трьох галузей виробництва, а також
обсяги кінцевих продуктів ( у грошових одиницях) задані у таблиці:
Продукція цехів Прямі витрати Кінцевий продукт
1 2 3
1 0,2 0,3 0,1 50
2 0,4 0,2 0,5 80
3 0,1 0,3 0,6 100
Потрібно знайти:
1) матрицю повних витрат;
2) план кожної галузі;
3) виробничу програму галузей;
4) коефіцієнти непрямих витрат.
Розв
’язування. Із таблиці видно, що матриця прямих витрат
буде:
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
6,03,01,0
5,02,04,0
1,03,02,0
A
.
Позначимо через
Х - вектор - план галузей виробництва, Y - ве
ктор кінцевих продуктів:
,
x
x
x
X
3
2
1
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
.
100
80
50
Y
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
Зв’язок між величинами, записаних в таблиці представимо у
вигляді системи лінійних рівнянь:
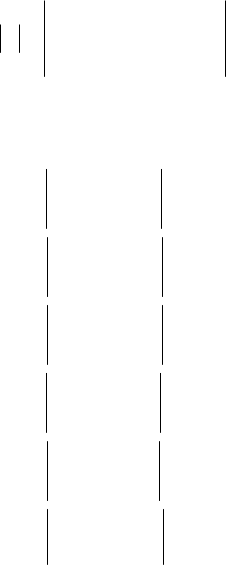
79
⎪
⎩
⎪
⎨
⎧
=++−
=++−
=++−
.100)x6,0x3,0x1,0(x
,80)x5,0x2,0x4,0(x
,50)x1,0x3,0x2,0(x
3213
3212
3211
В матричній формі маємо :
Х −AХ=Y , або (E−A)Х=Y.
Позначимо
E−A=B. Система лінійних алгебраїчних рівнянь
запишеться в матричній формі:
BX=Y. Звідси X= B
-1
Y.
В нашій задачі
.B
4,03,01,0
5,08,04,0
1,03,08,0
6,03,01,0
5,02,04,0
1,03,02,0
100
010
001
AE =
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−−
−−
−−
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=−
Для знаходження оберненої
В
-1
до матриці В, обчислимо ви-
значник:
.053,012,0048,0
008,0012,0015,0256,0
4,03,01,0
5,08,04,0
1,03,08,0
B
=−−
−−−−=
−
−−
−−
=
Тому для матриці
В існує обернена В
-1
. Знайдемо
алгебраїчні доповнення до елементів матриці
В :
;17,015,032,0
4,03,0
5,08,0
)1(b
2
11
=−=
−
−
−=
;11,0)05,016,0(
4,01,0
5,04,0
)1(b
3
12
=−−−=
−
−−
−=
;2,008,012,0
3,01,0
8,04,0
)1(b
4
13
=+=
−−
−
−=
;15,0)03,012,0(
4,03,0
1,03,0
)1(b
3
21
=−−−=
−
−−
−=
;31,001,032,0
4,01,0
1,08,0
)1(b
4
22
=−=
−
−
−=
;27,0)03,024,0(
3,01,0
3,08,0
)1(b
5
23
=−−−=
−
−
−=

80
;23,008,015,0
5,08,0
1,03,0
)1(b
4
31
=+=
−
−−
−=
;44,0)04,04,0(
5,04,0
1,08,0
)1(b
5
32
=−−−=
−−
−
−=
.52,012,064,0
8,04,0
3,08,0
)1(b
6
33
=−=
−
−
−=
Матриця з цих алгебраїчних доповнень буде:
,
52,044,023,0
27,031,015,0
2,011,017,0
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
а приєднана
.
52,027,02,0
44,031,011,0
23,015,017,0
B
П
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
=
Обернена матриця має вигляд :
.
81,909,577,3
3,885,508,2
34,483,221,3
52,027,02,0
44,031,011,0
23,015,017,0
053,0
1
B
1
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
≈
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
−
Елементи цієї матриці
B
-1
- це коефіцієнти повних витрат, а
сама матриця є матрицею коефіцієнтів повних витрат.
2) Для знаходження плану кожної галузі, помножимо
1
B
−
на
вектор кінцевих продуктів
:Y
.
x
x
x
1577
1402
821
100
80
50
81,909,577,3
3,885,508,2
34,483,221,3
YBX
3
2
1
1
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
≈
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
==
−
Значить:
.1577x;1402x;821x
321
===
Отже, якщо відомо обсяг кінцевої продукції (у грошових оди-
ницях)
,100y;80y;50y
321
=== то потрібно запланувати такі об-
сяги виробництва для першої галузі - 821, для другої - 1402 і для
третьої - 1577.
3) Для знаходження виробничої програми кожної галузі, знай-
демо добуток коефіцієнтів прямих витрат і валового випуску проду-
кції:
;2,1648212,0xax
11111
=⋅== ;6,42014023,0xax
21212
=⋅==
