Шинкарик М.І. Вища математика
Подождите немного. Документ загружается.


321
.Cx1ln
2
1
xarctgxdx
x1
x
xarctgxxdxarctg
2
2
++−=
+
−=
∫∫
в)
∫
β
α
dx)xsin(e
x
,
∫
α
α
dx)xcos(e
x
.
В цьому випадку вибір u і v несуттєвий.
Приклад 11. Знайти
∫
.xdxsine
x3
Розв
'язування. Виберемо u=
x3
e , а dv= xdxsin . Тоді
dxe3du
x3
= ,
.
x
cos
v
−= Отже
∫∫
+−= xdxcose3xcosexdxsine
x3x3x3
,
∫
xdxcose
x3
- інтегруємо за частинами. Знову виберемо u=
x3
e .
Тоді xdxcosdv = , xsinv = . Одержуємо
∫∫
−+−=
xdx
sine9xsine3соsxexdxsine
x3x3x3x3
.
Шуканий інтеграл є в правій і в лівій частинах рівності. Ви-
значимо його:
∫
+−= xsine3xcosexdxsine10
x3x3x3
.
Отже
∫
+
+−
= .C
10
xsine3xcose
xdxsine
x3x3
x3
Такі інтеграли інколи називають циклічними або коловими.
При їх інтегруванні обов'язково за
u двічі вибирати ту ж саму
функцію.
Зауваження: В випадку, якщо підінтегральний вираз є добут-
ком многочлена на одну з розглянутих функцій, можна інтеграл
розкласти на суму декількох інтегралів. Наприклад,
∫∫∫∫
+−=+− dxе2dxхе3dxех2dxе)2х3х2(
х2х2х22х22
.
1.5. Інтегрування раціональних дробів
Функціями, які завжди інтегруються, є раціональні дроби. Не-
хай
n
n
2
210
xa...xaxaa)x(P ++++=
і
m
m
2
210
xb...xbxbb)x(Q ++++=
два многочлени з дійсними
коефіцієнтами. Вираз
)x(Q
)x(P
називається раціональним дробом.
Якщо степінь чисельника менша за степінь знаменника, то
дріб називається правильним. Якщо ж степінь чисельника більша

322
або дорівнює степеневі знаменника то дріб називається неправиль-
ним. Так, наприклад,
25
3
x6x2
7x4x5
−
+−
- правильний дріб, а дріб
4x8x6
9x3x5x7
2
35
−+
−+−
- неправильний.
Теорема Вейєрштраса про наближення
. Будь-яку функцію
f(x), неперервну на (а,b), можна з наперед заданою довільною
похибкою замінити многочленом
n
n
2
210
xa...xaxaa)x(P ++++= .
Тобто, практично, багато інтегралів можна звести до
інтегрування раціональних функцій. З алгебри відомо, що всякий
многочлен можна розкласти на добуток множників виду (
bx −
) та
(
qpxx
2
++ ), так званих незвідних многочленів, де ( qpxx
2
++ ) –
квадратний тричлен, який немає дійсних коренів. І всякий правиль-
ний дріб можна розкласти на суму простих:
b
x
А
−
,
k
)bx(
В
−
,
qpxx
NМx
2
++
+
,
r2
)qpxx(
NMx
++
+
. (6.20)
Це роблять методом невизначених коефіцієнтів.
◙ Метод невизначених коефіцієнтів
Метод невизначених коефіцієнтів дає алгоритм для знаход-
ження коефіцієнтів розкладу правильного раціонального дробу на
суму простих.
Нехай
=
++++β−α−
++++
=
t2l2nm
k
k
2
210
)srxx...()qpxx...()x...()x(
xa...xaxaa
)x(Q
)x(P
++
β−
+
β−
++
α−
++
α−
+
α−
= ...
)x(
B
x
B
...
)x(
A
...
)x(
A
x
A
2
21
m
m
2
21
.
)srxx(
FxE
...
)srxx(
FxE
srxx
FxE
...
)qpxx(
NxM
...
)qpxx(
NxM
qpxx
NxM
...
)x(
B
t2
ll
22
22
2
11
l2
ll
22
22
2
11
n
n
++
+
++
++
+
+
++
+
+
+
++
+
++
++
+
+
++
+
++
β−
+
Зводимо праву частину рівності до спільного знаменника.
Прирівнюємо відповідні коефіцієнти чисельника лівої частини з
коефіцієнтами чисельника правої. Отримуємо систему лінійних
алгебраїчних рівнянь. Розв’язки її є коефіцієнтами розкладу.
(6.21)

323
Приклад 12.
+
+
+
−
+
−
=
+++−
−+
)4x(
B
)6x(
A
6x
A
)11x3x)(4x()6x(
9x3x5
2
21
322
3
32
33
22
22
2
11
)11x3x(
NxM
)11x3x(
NxM
11x3x
NxM
++
+
+
++
+
+
++
+
+
.
Це приклад розкладу правильного раціонального дробу на су-
му простих, де
А
1
, А
2
, В, М
і
, N
і
-невизначені коефіцієнти.
Приклад 13. Знайти інтеграл
dx
10
хх
8х9
3
∫
−+
+
.
Розв
’язування.
10хх
8х9
3
−+
+
- правильний дріб. Розкладаємо
знаменник на добуток незвідних множників:
)5х2х)(2х(10хх
23
++−=−+ . Для рівняння 05х2х
2
=++ ,
D=4-20<0. Тому рівняння немає дійсних коренів.
Отже
5х2х
NМх
2х
А
)5х2х)(2х(
8
х9
10
хх
8х9
223
++
+
+
−
=
++−
+
=
−+
+
.
Звівши до спільного знаменника і прирівнявши чисельники
одержимо:
N2A5x)NМ2А2(х)МА(8х9
2
−++−++=+ .
Прирівнюючи відповідні коефіцієнти отримуємо:
⎪
⎩
⎪
⎨
⎧
=−
=+−
=+
.8N2А5
,9NМ2А2
,0МА
⇒
⎪
⎩
⎪
⎨
⎧
=−−
=+−
−=
.8N2M5
,9NМ4
,МА
;M49N += ;818M13 =−− ;26M13 =− ;2M −= ;1N =
2
A
= .
Ми одержали інтеграли від дробів (6.20). Отже:
∫∫∫∫
++
+−
+
−
=
++
+−
+
−
=
−+
+
dx
5
х2х
1х2
dx
2
х
2
dx)
5
х2х
1х2
2
х
2
(dx
10
хх
8х9
223
Знайдемо, відповідні простим дробам (6.20) інтеграли, а потім за-
вершимо приклад, використавши одержані результати.
◙ Інтеграли від найпростіших раціональних дробів
а)
∫
+−=
−
CbxlnА
b
x
Аdx
. (6.21)
При розв’язуванні використано формулу (6.7) та табличний
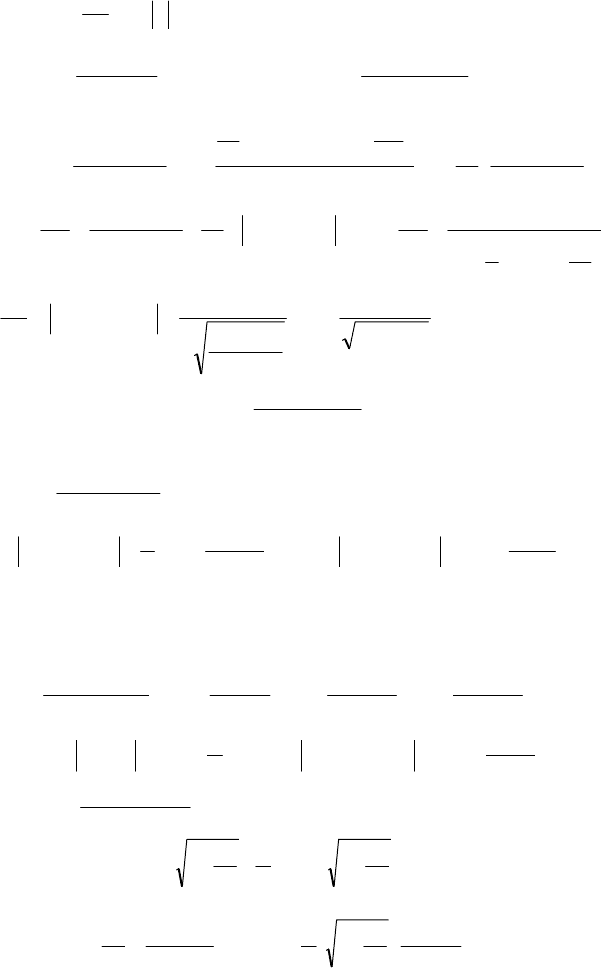
324
інтеграл
∫
+= Culn
u
du
.
б)
∫∫
+
+−
−
=−=
−
+−
−
C
1k
)bx(
Вdx)bx(В
)bx(
Вdx
1k
k
k
. (6.22)
в)
∫∫∫
+
++
+
=
++
−++
=
++
+
dx
gpxx
px2
2
M
dx
gpxx
)
2
Mp
N()px2(
2
M
dx
gpxx
NMх
222
∫∫
=−+++=
++
−+
−++ )
4
p
g()
2
p
x(
2
2
dx
)
2
Mp
N(gpxxln
2
M
gpxx
dx
)
2
Mp
N(
2
2
.C
pg4
px2
arctg
4
pg4
2
MpN2
gpxxln
2
M
22
2
+
−
+
−
−
−++=
(6.23)
Приклад 14. Знайти
∫
+−
−
dx
8x4x
2x2
2
.
Використовуючи формулу (6.23) запишемо
=
+−
−
∫
dx
8x4x
2x2
2
C
2
2х
arctg8x4xlnC
2
4x2
arctg
4
4
8x4xln
22
+
−
−+−=+
−
−+−=
.
Проте, на практиці, цю громіздку формулу застосовують рідко
а інтеграл шукають, виділивши в знаменнику повний квадрат.
2222
2)2x(44x4x8x4x +−=++−=+−
. Зробимо заміну (х-2)=u.
Тоді
∫∫∫∫
=
+
+
+
=
+
+
=
+−
−
du
2u
2
du
2u
u2
du
4u
2u2
dx
8x4x
2x2
222222
C
2
2x
arctg4)2x(lnC
2
u
arctg4uln
22
+
−
++−=+++=
.
г)
∫
++
+
dx
)gpxx(
NMх
k2
. Виділивши в знаменнику повний квадрат,
визначаємо заміну:
2
p
4
p
qtx
2
−−=
,
dt
4
p
qdx
2
−=
.Ввівши її, одержуємо суму
двох
виразів:
∫∫
+
−⋅−+
+
−
k2
2
k2
2
)1t(
dt
4
p
q)
2
p
MN(
)1t(
tdt
)
4
p
q(M
.
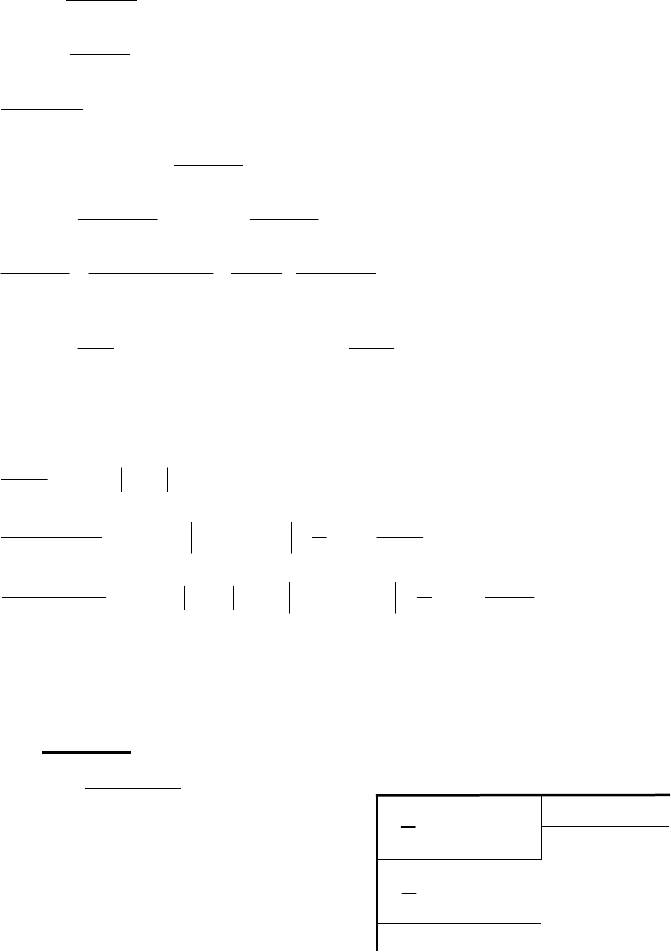
325
Інтеграл
∫
+
k2
)1t(
tdt
знаходимо, наприклад, новою заміною
u1t
2
=+
,
dutdt =
.
Інтеграл
∫
+
k2
)1t(
dt
знайдемо, вивівши рекурентну формулу.
=+−+=+=
+
∫∫∫
+−+−+−
−
1k21k21k2
1k2
)1t(td)1t(tdt)1t(
)1t(
dt
++=
+
−++=
+−+−
∫
1k2
k2
2
1k2
)1t(t
)1t(
dtt2
)1k()1t(t
і далі
.
)1t(
dt
)1k(2
)1t(
dt
)1k(2
k21k2
∫∫
+
−−
+
−+
−
∫∫
−
+−
−
+
+−
=
+
1k22k2
)1t(
dt
2k2
3k2
)1t)(1k(2
t
)1t(
dt
. Це є рекурентна формула, якою
понижується порядок знаменника. Використавши її (к-1) раз приходимо до
інтеграла
∫
+1t
dt
2
, який є табличним.
∫
+=
+
Carctgt
1t
dt
2
.
Ми розглянули чотири випадки до яких зводиться
інтегрування правильних раціональних дробів.Завершимо
розв’язування прикладу 13, використовуючи виведені формули:
C2xln2dx
2х
2
+−=
−
∫
.
C
2
2x
arctg
2
3
5x2xln2dx
5
х2х
1х2
2
2
+
+
−++−=
++
+−
∫
. Отже:
C
2
2x
arctg
2
3
5x2xln22xln2dx
10
хх
8х9
2
3
+
+
−++−−=
−+
+
∫
.
◙ Інтегрування неправильних раціональних дробів
Інтегрування неправильних раціональних дробів зводиться
(після виділення цілої частини дробу) до інтегрування многочлена
та інтегрування правильного раціонального дробу.
Приклад
. 15 . Обчислити
інтеграл
dx
2xx
1x
2
3
∫
−−
−
.
Розв
’язування. Раціональний дріб не-
правильний. Виділяємо цілу частину і
записуємо його в вигляді суми цілої і
дробової частин.
1x
3
−
2xx
2
−−
x2xx
23
−−
x+1
1x2x
2
−+
2xx
2
−−
3x+1
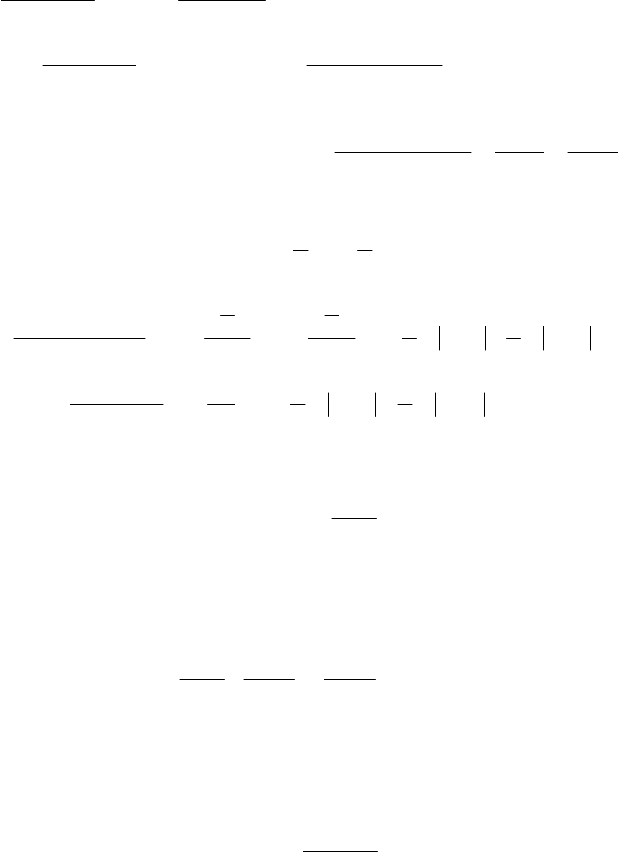
326
2xx
13x
1x
2
−−
+
++=
−−
−
2xx
1x
2
3
. Тоді
()
∫∫∫
−+
+
++=
−−
−
dx
)2x)(1x(
1x3
dx1xdx
2xx
1x
2
3
.
Використовуючи метод невизначених коефіцієнтів
розкладаємо дріб на суму простих:
2x
B
1x
A
)2x)(1x(
1x3
−
+
+
=
−+
+
;
;BBxA2Ax1x3 ++−=+
)BA2(x)BA(1x3 +−++=+ ;
⎩
⎨
⎧
=+−
=+
.1BA2
,3BA
3А=2; А=
3
2
; В=
3
7
. Одержимо:
∫∫∫
+−++=
−
+
+
=
−+
+
.C2xln
3
7
1xln
3
2
dx
2x
3
7
dx
1x
3
2
dx
)2x)(1x(
1x3
Отже
C2xln
3
7
1xln
3
2
x
2
x
dx
2xx
1x
2
2
3
+−++++=
−−
−
∫
.
◙ Метод Остроградського інтегрування раціональних функцій.
Це метод виділення алгебраїчної частини в невизначених інтегралах від
раціональних функцій. Нехай Р(х) і Q(x)- многочлени з дійсними коефіцієнтами.
Степінь Р(х) менша за степінь Q(x). Тобто
)x(Q
)x(P
- правильний раціональний дріб і
t2l2nm
)srxx...()qpxx...()x...()x()x(Q ++++β−α−= .
Нехай, також
1t21l21n1m
1
)srxx...()qpxx...()x...()x()x(Q
−−−−
++++β−α−=
і
)srxx)...(qpxx)...(x)...(x()x(Q
22
2
++++β−α−=
-многочлени. То існують
многочлени Р
1
(х), Р
2
(х), степені яких менші за степені Q
1
(x), Q
2
(x) відповідно, такі
що
∫∫
+= dx
)x(Q
)x(P
)x(Q
)x(P
)x(Q
)x(P
2
2
1
1
. (6.25)
Коефіцієнти многочленів Р
1
(х) і Р
2
(х) можна знайти методом невизначених
коефіцієнтів продифиренціювавши (6.25). Q
1
(x) є найбільшим спільним дільником
Q(x) і його похідної Q
΄
(x) і можна визначити за допомогою метода Евкліда.
Q
2
(x) = Q(x)/Q
1
(x). Формула зводить інтегрування правильного раціонального дро-
бу до інтегрування правильного раціонального дробу, знаменник якого має прості
корені.
Приклад 16 . Знайти інтеграл
dx
)1x(
1
23
∫
+
.
Розв’язування. Розкладемо многочлен
)1x(
3
+
на прості множники
)1xx)(1x()1x(
23
+−+=+
. Тоді, за методом Остроградського, запишемо
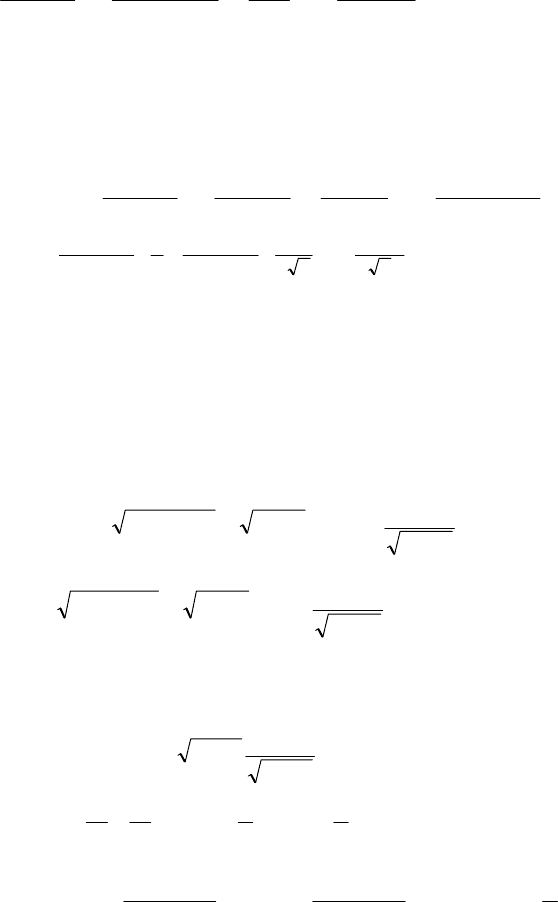
327
dx
1xx
NMx
dx
1x
D
1x
CBxAx
dx
)1x(
1
23
2
23
∫∫∫
+−
+
+
+
+
+
++
=
+
.
Диференціюємо цей вираз і зводимо до спільного знаменника.
Прирівнюємо чисельники:
++−++−+++−−−= )1xxxxx(DBAx2Cx3Bx2Ax1
2345234
)1xxx)(NMx(
24
+++++ . Прирівнюючи відповідні коефіцієнти, одержуємо
0=D+N; 0= −A−D+M+N; 0= −2B+D+N; 0= −3C+D+M; 0=2A−D+M+N; 1=B+D+N.
Розв’язком цієї системи рівнянь є: A=C=0; B=1/3; D=2/9; M= −2/9; N=4/9.
Отже
=
+−
−
+
+
+
+
=
+
∫∫∫
dx
)1xx(9
)2x(2
dx
)1x(9
2
)1x(3
x
dx
)1x(
1
2323
)1x(.C
3
1x2
arctg
33
2
1xx
)1x(
ln
9
1
)1x(3
x
2
2
3
−≠+
−
+
+−
+
+
+
=
.
1.6. Інтегрування тригонометричних функцій
При інтегруванні тригонометричних функцій важливо вміти використовува-
ти тригонометричні формули, вдало підібраною заміною або підстановкою, звести
інтеграл до простішого (дробово-раціонального виразу), а в результаті і до таблич-
ного. Є деякі види інтегралів (проте не всі) для яких є правила їх знаходження.
а) Інтеграли виду
∫
⋅ .xdxcosxsin
nm
Якщо хоча б одне із чисел m або n додатне ціле непарне число, наприклад
m, то вводимо заміну cosx=t. Тоді
22
t1xcos1xsin −=−= ,
2
t1
dt
dx
−
−=
.
Якщо ж n – додатне непарне, то sinx= t,
22
t1xsin1xcos −=−=
,
2
t1
dt
dx
−
=
.
Приклад 17. Знайти
∫
⋅ xdxcosxsin
23
Розв’язування.
∫∫
=⋅=⋅ xdxsinxcosxsinxdxcosxsin
2223
∫∫
=−−=
−
−−−= dt)tt(
t1
dt
t1t)t1(
42
2
222
.Cxcos
5
1
xcos
3
1
C)
5
t
3
t
(
53
53
++−=+−−=
Якщо m та n парні невід’ємні числа, то понижають степені за формулами:
;
2
x2cos1
xcos
2
+
=
;
2
x2cos1
xsin
2
−
=
x2sin
2
1
xcosxsin =
.
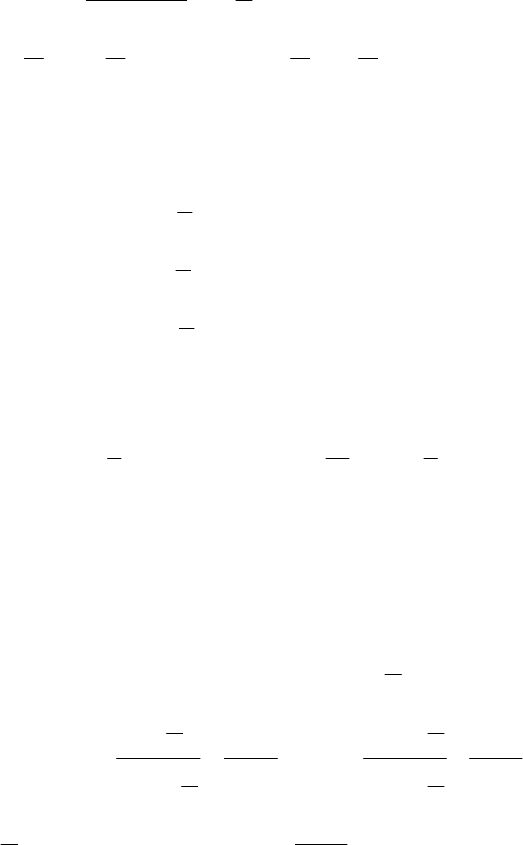
328
Приклад 18. Знайти
∫
xdxcos
2
Розв
’язування.
()
=+=
+
=
∫∫∫
dxx2cos1
2
1
dx
2
x2cos1
xdxcos
2
.Cx2sin
4
1
x
2
1
C)x2sin
2
1
x(
2
1
++=++=
б)Інтеграли виду
∫
nxdxcosmxsin
,
∫
nxdxsinmxsin
,
∫
nxdx
cosmxcos
.
Ці інтеграли спрощуються застосуванням формул перетворення до-
бутку тригонометричних функцій в суму:
∫∫
−++= dx)x)nmsin(x)nm(sin(
2
1
nxdxcosmxsin
,
∫∫
+−−= dx)x)nmcos(x)nm(cos(
2
1
nxdxsinmxsin
,
∫∫
++−= .dx)x)nmcos(x)nm(cos(
2
1
nxdxcosmxcos
Такі інтеграли мають широке застосування в теорії рядів Фур’є.
Приклад 19. Знайти
∫
xdx3cosx5sin
.
∫∫
+−−=+= .Cx2cos
4
1
x8cos
16
1
dx)x2sinx8(sin
2
1
xdx3cosx5sin
в) Інтеграли виду
∫
,dx)xcos,x(sinR
універсальна тригонометрична підстановка.
Для інтегралів виду
∫
,dx)xcos,x(sinR де )xcos,x(sinR -
раціональна функція відносно
xcos,xsin
, часто застосовують
універсальну підстановку. Це підстановка
.t
2
x
tg =
(6.26)
Тоді:
2
2
t1
t2
2
x
tg1
2
x
tg2
xsin
+
=
+
=
,
2
2
2
2
t1
t1
2
x
tg1
2
x
tg1
xcos
+
−
=
+
−
=
,
arctgt
2
x
=
, arctgt2x = ,
.
t1
dt2
dx
2
+
=
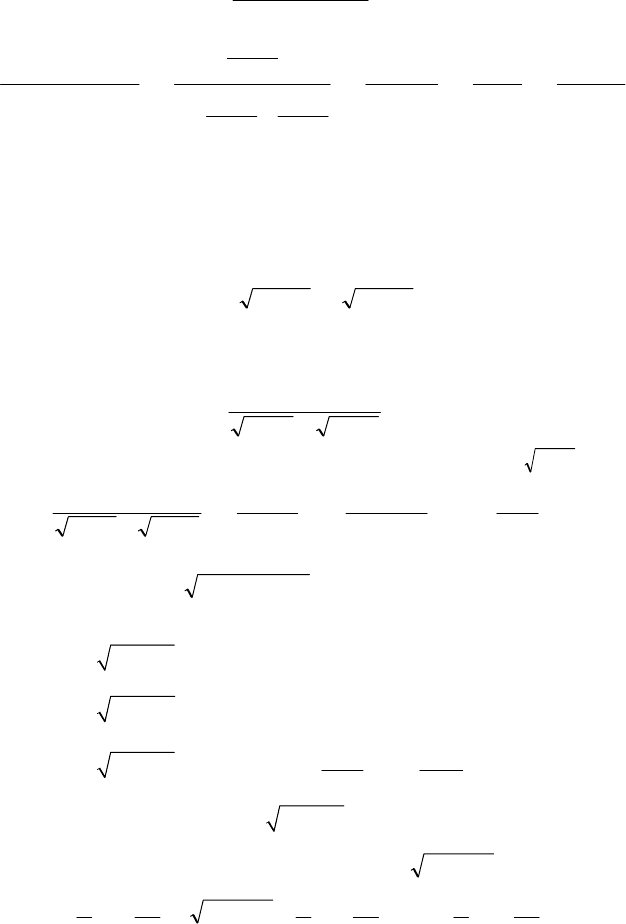
329
Приклад 20. Знайти
∫
−+ xcosxsin1
dx
.
∫∫ ∫∫∫
+
=
+
=
+
=
+
−
−
+
+
+
=
−+ )1t(t
dt
tt
dt
t2t2
dt2
t
1
t1
t
1
t2
1
t1
dt2
xcosxsin1
dx
22
2
2
2
2
і далі інтегруємо як раціональний дріб. (Пункт 6.1.5.)+
Інтегрування тригонометричних функцій та інтегрування
ірраціональних функцій, вдало підібраною заміною, часто зводиться до
інтеграла від раціонального дробу, який завжди інтегрується.
1.7. Інтегрування деяких ірраціональних функцій
Інтеграли виду
,dx)bax,...,bax,x(R
nm
++
∫
зводяться до інтег-
ралів від раціональних функцій за допомогою підстановки
,tbax
k
=+
де
k - найменше спільне кратне чисел m,..., n.
Приклад 21. Знайти
∫
−+− 3x3x
dx
3
.
Розв
’язування. Використано заміну: x-3=t
6
, dtt6dx
5
= ,
6
3xt −=
.
...dt
1t
t
6dt
)1t(t
t
6
tt
dtt6
3x3x
dx
3
2
5
32
5
3
∫∫∫∫
=
+
=
+
=
+
=
−+−
А далі шукаємо інтеграл від раціональної функції.(Пункт 6.1.5.)
Інтеграли
dx)cbxax,x(R
2
∫
++ можна звести, виділивши під
знаком радикала повний квадрат, до трьох таких інтегралів:
(
)
22
,,
Rx a x dx
−
∫
вводимо заміну
tsinax =
(
t
cos
a
x
=
).
(
)
22
,,
R
xa xd
x
+
∫
заміна
atgt
x
=
(
actgt
x
=
).
(
)
22
,,
Rx x a dx
−
∫
заміна
t
sin
a
x =
(
t
cos
a
x =
).
Для інтегралів виду
(
)
22
,,
R
xx ad
x
±
∫
часто використовують
підстановку (підстановка Ейлера)
22
axxt ±+=
,
)
t
a
t(
2
1
x
2
∓=
,
)
t
a
t(
2
1
ax
2
22
±=±
, dt)
t
a
1(
2
1
dx
2
2
±= .
330
На закінчення треба зауважити, що різні способи інтегрування
можуть привести до різних аналітичних виразів первісної. Проте ми
отримуємо вирази, які відрізняються хіба, що на сталу.
1.8. Поняття про невизначений інтеграл, що не має
первісних в елементарних функціях
До цього моменту ми вдало розв’язували задачу знаходження
невизначеного інтеграла для функції. Проте
, ми побачили, що це
завдання не є простим. Більше того, доведено, що є ряд функцій,
первісна для яких не може бути представлена, як вираз утворений
“елементарними” функціями. Наведемо,як приклад, деякі такі інтег-
рали:
dxe
2
x
∫
−
,
∫
dx
x
xsin
,
∫
x
ln
dx
, dxxsink1
22
∫
− (
1k <
).
§ 2. Визначений інтеграл
При розв’язуванні деяких важливих задач необхідно знаходи-
ти нескінченну суму нескінченно малих доданків. Це приводить до
одного з центральних понять математики – визначеного інтеграла.
2.1. Задачі, що приводять до поняття визначеного інтеграла
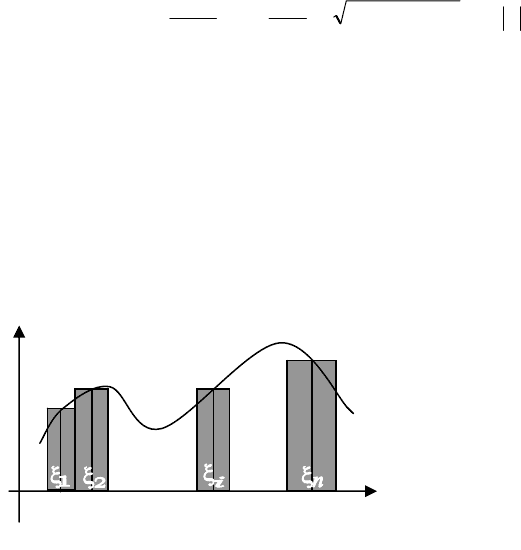
◙ Задача про площу криволінійної трапеції
Знайдемо площу
фігури, яка обмежена
графіком неперервної
функції
)x(fy = на
відрізку
[]
b,a
, віссю абс-
цис, та прямими
a
x
=
та
.bx=
Називатимемо її
криволінійною трапецією
(мал. 2). Для простоти,
розглянемо випадок, коли
0)x(f ≥ на даному відрізку
[]
b,a .
Розіб’ємо проміжок
[]
b,a
на n відрізків
[]
i1i
x,x
−
(i=1,2,3…n),
,ax
0
=
bx
n
=
. На кожному з відрізків
[]
i1i
x,x
−
виберемо по
довільній точці
[]
i1ii
x,x
−
∈
ξ
(i=1,2,3…n). Тоді площа і- го прямо-
х
у
a х
1
х
2
1−i
x
i
x
1−n
x b
0
Мал.2
