Шинкарик М.І. Вища математика

301

⎪

⎩

⎪

⎨

⎧

=−λ=

λ∂

=−λ=

λ∂

=

∂

λ+

∂

=

∂

λ∂

=

∂

λ+

∂

=

∂

λ∂

∑

=

.0b),X(q

),X(L

.........................................................

,0b),X(q

),X(L

,0

x

)X(q

x

)X(u

x

),X(L

.............................................................

,0

x

)X(q

x

)X(u

x

),X(L

m

*

m

*

1

*

1

*

n

1j

n

*

j

n

*

n

*

n

1j

1

*

j

1

*

1

*

(5.15)

Із системи рівнянь знаходимо координати точки

),x,...,x,x(X

*

n

*

2

*

1

*

в якій досягається екстремум. Значення

n1

,...,λλ

при цьому ролі не грають. Характер екстремальності точок

)x,...,x,x(X

*

n

*

2

*

1

*

визначаємо з допомогою достатніх умов, які за-

стосовуються тільки до функції

),x(u

оскільки

,0b)x(q

ii

=−

).m,1i( =

Приклад 1. Знайти екстремум функції

21

2

221

2

1

x4x2xxxx2z −+++= при умові .2xx

21

=+

Розв

’язування. Запишемо обмеження у виді

.02xx

21

=−+

Функція Лагранжа матиме вид:

)2xx(x4x2xxxx2),x,x(L

2121

2

221

2

121

−+λ+−+++=λ .

Знаходимо частинні похідні першого порядку

,2xx4

x

L

21

1

λ+++=

∂

,4x2x

x

L

21

2

λ+−+=

∂

.2xx

L

21

−+=

λ∂

∂

Використовуючи необхідну умову екстремуму, складаємо си-

стему рівнянь:

)1(

0

2xx

4x2x

2xx4

21

−×

⎪

⎩

⎪

⎨

⎧

=

−+

λ+−+

λ+++

.

302

Виключимо λ з перших двох рівнянь. Помножимо друге рів-

няння на число (-1) і додамо до першого рівняння. В результаті

отримаємо систему рівнянь:

.3x;1x

04x4

06xx3

02xx

06xx3

21

1

21

=−=⇒

⎪

⎩

⎪

⎨

⎧

=+

=+−

⇒

⎩

⎨

⎧

=−+

=+−

Отже, точка

)3;1(X

*

−

є точкою підозрілою на екстремум.

Складаємо матрицю Гесса:

;1)xx4(

xxx

L

;4)xx4(

x

L

21

221

2

21

1

2

1

2

=+

∂

=

∂∂

∂

=+

∂

=

∂

;2)x2x(

x

L

21

2

=+

∂

=

∂

.07

21

14

M;04M;

21

14

)X(H

21

*

>==>=

⎥

⎦

⎤

⎢

⎣

⎡

=

Отже, в точці

)3;1(X

*

−

маємо

min

z

:

.634)1(233)1()1(2z

22

min

−=⋅−−⋅++⋅−+−=

З геометричної точки зору

)X(z

*

min

досягається в вершині

параболи, яка отримується в результаті перетину параболоїда

21

2

221

2

1

x4x2xxxx2z −+++= з площиною .02xx

21

=−+

§11. Емпіричні формули. Побудова формули лінійної

залежності методом найменших квадратів

При розв'язуванні практичних задач часто виникає ситуація,

коли аналітичний вигляд функції не заданий, але ця функція задана

таблично, тобто:

x

1

x

2

x

…

i

x

…

n

x

y

1

y

2

y

…

i

y

…

n

y

Такі таблиці отримують в результаті дослідів (експериментів),

тому їх називають емпіричними таблицями. За заданою емпірич-

ною таблицею потрібно знайти аналітичний вид функції. В загаль-

ному випадку це досить складна задача і розв’язується вона неодно-

значно. Одним із найбільш поширених методів знаходження аналі-

303

тичного виду відповідної функції є метод найменших квадратів. Цей

метод часто використовується в статистиці та економічних дослі-

дженнях.

Розглянемо випадок, коли зв’язок між

x

і

y

прямолінійний,

тобто

bkxy += .

Нехай задана емпірична таблиця. Розглянемо на площині

y0x

точки

).y;x(M),...,y;x(M),...,y;x(M);y;x(M

nnniii222111

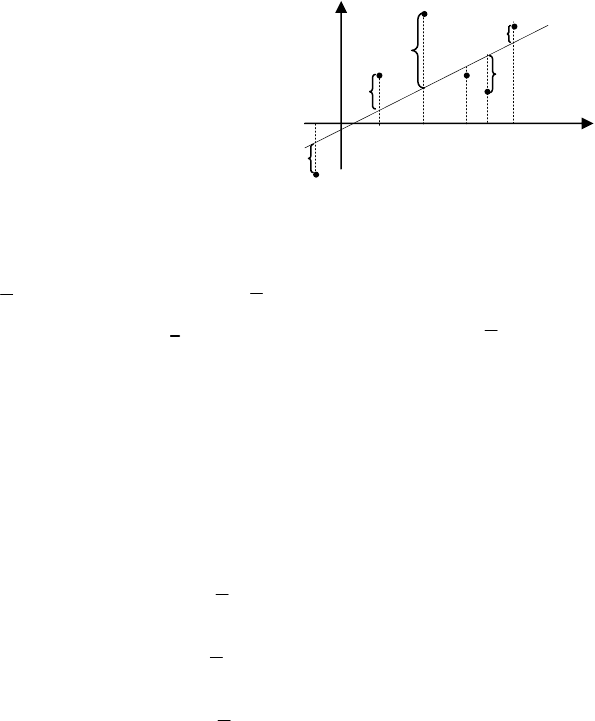
Оскільки між х і у існує прямолі-

нійний зв’язок, то ці точки будуть

розміщені на площині хОу так, що

через них можна наближено про-

вести пряму лінію. Побудуємо від-

повідний малюнок (мал. 12).

Нам відомо, що рівняння цієї

прямої буде

bkxy +=

, де k і b

деякі невідомі параметри. З кожної точки

)n,...,2,1i(M

i

= опусти-

мо перпендикуляри на вісь

x0 і продовжимо їх до перетину з пря-

мою лінією. Ординати точок перетину з прямою

bkxy += позна-

чимо

).n,...,2,1i(y

i

=

Різницю

i

yy − позначимо через

i

δ

і назве-

мо її нев’язкою (похибкою). Очевидно, що числа

i

і

yy −=δ мо-

жуть приймати довільні значення.

Складемо суму квадратів нев’язок, тобто:

∑

=

δ=δ++δ+δ=

n

1i

2

i

2

n

2

1

....)b,k(F

Тепер сформулюємо задачу: потрібно вибрати положення

прямої

bkxy +=

так, щоб величина

F

приймала мінімальне зна-

чення. Аналітично цю задачу розв’язуємо так: припустимо, що фун-

кція

bkxy +=

задана. Знайдемо значення нев’язок:

;ybkxyy

111

1

−+=−=δ

..............................................

;ybkxyy

iii

i

−+=−=δ

.............................................

.ybkxyy

nnn

n

−+=−=δ

δn

х

1

х

i

х

2

х

3

х

n

О

х

у

Мал

.

12

δi

δ

3

δ

2

δ

1

х

4

М

4

М

i

М

1

М

2

М

n

М

3

304

Підставимо ці значення

i

δ

в

:)b,k(F

(

∑

=

−+=

n

1i

2

ii

.)ybkx)b,k(F

Таким чином , задача зводиться до знаходження мінімуму фу-

нкції

)b,k(F

відносно змінних k і .b Запишемо необхідну умову

екстремуму:

⎪

⎩

⎪

⎨

⎧

=

∂

=

∂

.0

b

)b,k(F

,0

k

)b,k(F

Знайдемо частинні похідні і підставимо їх в рівняння:

⎪

⎩

⎪

⎨

⎧

=−+=

∂

=⋅−+=

∂

∑

=

n

1i

ii

n

1i

iii

.0)ybkx(2

b

)b,k(F

,0x)ybkx(2

k

)b,k(F

Виконавши відповідні елементарні перетворення, в кінцевому

результаті отримаємо систему рівнянь:

⎪

⎩

⎪

⎨

⎧

=+

∑∑

∑∑∑

==

===

n

1i

n

1i

ii

n

1i

n

1i

n

1i

iii

2

i

.ynbxk

,y,xxbxk

.

Ця система називається нормальною системою рівнянь

методу найменших квадратів. З неї знаходимо

k і b і підставляє-

мо в формулу

.bkxy += Для практичного розв’язування задач зру-

чно користуватися розширеною емпіричною таблицею, яка одержу-

ється таким чином: до вихідної таблиці додаємо два рядки для

2

x та

xy

і один стовпчик, в якому записуємо відповідні суми, що входять

у нормальну систему. В результаті отримаємо таку таблицю:

x

1

x

2

x

...

n

x

∑

i

x

y

1

y

2

y

...

n

y

∑

i

y

2

x

2

1

x

2

x

...

2

n

x

∑

2

i

x

xy

11

yx

22

yx

...

nn

yx

∑

ii

yx

305

Дані останнього стовпчика таблиці підставляємо в нормальну

систему рівнянь.

Приклад 1. Дано таблицю

x

-1 0 1 3 5

y

-0,9 1,2 2,8 7,1 10,8

Знайти коефіцієнти прямолінійного зв’язку між

x

і

y

.

Розв

’язування. Будуємо розширену таблицю.

x

-1 0 1 3 5 8

y

-0,9 1,2 2,8 7,1 10,8 21

2

x

1 0 1 9 25 36

xy

0,9 0 2,8 21,3 54 79

За таблицею складаємо систему рівнянь при

:5n =

⎩

⎨

⎧

=+

.21b5k8

,79b8k36

Домножимо друге рівняння на (-1,6) і додамо до першого.

Одержимо:

⎩

⎨

⎧

=

⇔

⎩

⎨

⎧

=+

=

.06,1b

96,1k

.21b5k8

4,45k2,23

Відповідь:

.06,1x96,1y +=

§12. Побудова емпіричних формул у випадку нелінійної

залежності

12.1. Параболічна залежність

Нехай залежність між змінними величинами задається форму-

лою

.cbxaxy

2

++= Така

залежність називається па-

раболічною. Скористаємося

методом найменших квад-

ратів для знаходження кое-

фіцієнтів

.c,b,a

Допустимо, що нам

задана емпірична таблиця,

за якою будуємо малюнок

(мал.13).

х

1

х

2

х

3

х

i

х

n

M

δ

n

δ

2

δ

1

δ

і

Мал.13

δ

3

306

За аналогією з лінійною залежністю розглянемо суму квадра-

тів нев’язок:

∑

=

δ=

n

1i

2

i

,)c,b,a(F де

,yy

iii

−=δ

а ,cbxaxy

i

2

i

++= .n,...,2,1i =

Підставивши замість

i

δ їх значення в ),c,b,a(F отримаємо:

∑

=

−++=

n

1i

2

ii

2

i

.)ycbxax()c,b,a(F

Накладемо вимогу, щоб функція

)c,b,a(F досягла мінімуму,

і запишемо необхідну умову існування екстремуму:

⎪

⎩

⎪

⎨

⎧

=

∂

=

∂

=

∂

.0

c

)c,b,a(F

,0

b

)c,b,a(F

,0

a

)c,b,a(F

Розписавши систему рівнянь в розгорнутому вигляді і викона-

вши відповідні елементарні перетворення , одержимо нормальну

систему рівнянь для випадку параболічної залежності:

⎪

⎩

⎪

⎨

⎧

=⋅++

=++

∑∑∑

∑∑∑∑

===

====

n

1i

i

n

1i

i

n

1i

2

i

n

1i

n

1i

ii

n

1i

n

1i

2

i

3

i

n

1i

n

1i

n

1i

n

1i

i

2

i

2

i

3

i

4

i

.yncxbxa

,yxxcxbxa

12.2. Нелінійні залежності, які зводяться до лінійних.

Гіперболічна залежність

Нехай залежність між змінними

x і y, які задані емпіричною

таблицею, задається формулою

.bx1

ax

y

+

=

Така залежність називається гіперболічною. Виконаємо пе-

ретворення змінних:

.

a

b

x

1

a

1

a

b

ax

1

y

1

+⋅=+=

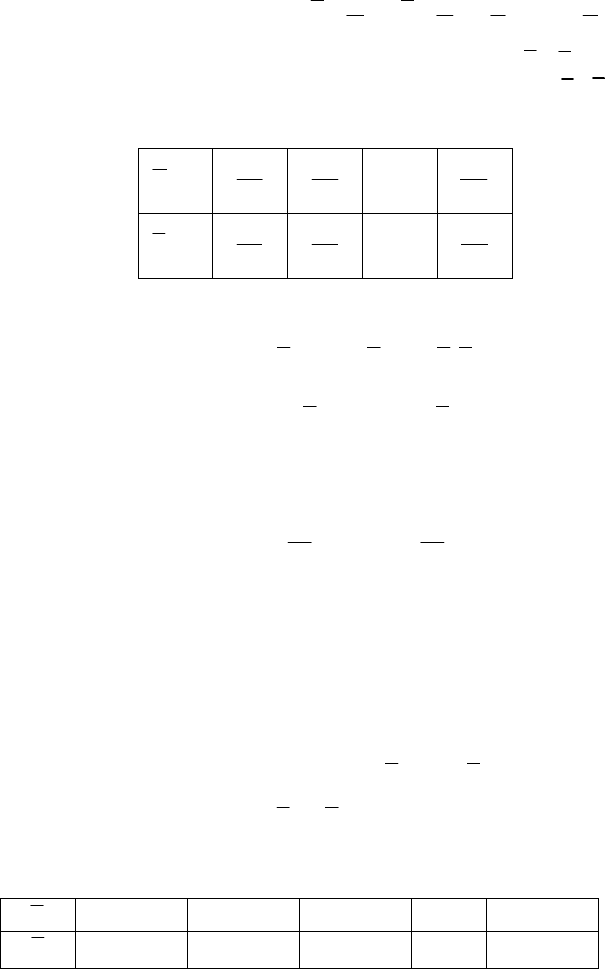
307

Введемо нові позначення:

.b

a

b

;a

a

1

;

y

1

y;

x

1

x

11

====

Тоді вихідне рівняння можна записати у вигляді:

y=ax+b

1

.

Очевидно, що залежність між змінними величинами

x і y є лі-

нійною. Потрібно знайти значення а

1

і b

1

. Для цього складемо нову

емпіричну таблицю.

x

1

x

1

2

x

1

…

n

x

1

y

1

y

1

2

y

1

…

n

y

1

Для цієї емпіричної таблиці складемо нормальну систему рів-

нянь для а

1

і b

1

. Oтримаємо:

⎪

⎩

⎪

⎨

⎧

=⋅+

=+

∑∑

∑∑∑

==

===

n

1i

n

1i

i

1

i

1

n

1i

n

1i

n

1i

i

ii

1

2

i

.ynbxa

,yxxbxa

Знайшовши із цієї системи значення

1

a

і

1

b

, знаходимо від-

повідні значення

a

і b:

;

a

1

a

1

= .

a

b

abb

1

==

12.3.Показникова залежність

Припустимо, що залежність між

x

і

y

задана формулою

,Bey

kx

=

тобто зв’язок заданий за допомогою показникової функ-

ції. Потрібно знайти коефіцієнти

B

і k .

Прологарифмуємо вираз

kx

Bey = при основі

e

, одержимо:

.kxBlnyln +=

Ввівши позначення ,Blnb,ylny,xx ===

отримаємо таку залежність:

.bxky += Для знаходження k і

B

мо-

жна скористатись нормальною системою рівнянь, перейшовши по-

передньо до нової емпіричної таблиці.

x

1

x

2

x

3

x

...

n

x

y

1

yln

2

yln

3

yln

…

n

yln

308

Тоді

B

знаходимо за формулою

b

eB =

, знайдені значення

B

і

k підставимо у вихідну формулу.

12.4. Степенева залежність

Нехай змінні

x

і

y

зв’язані формулою .Bxy

k

= Пролога-

рифмуємо цю функцію (при

0x > ): .xlnkBlnyln += Ввівши нові

позначення

,xlnx =

,ylny =

,Blnb = знову приходимо до лінійної

залежності

.bxky +=

Щоб скористатись нормальною системою рівнянь для знахо-

дження

k і ,b складаємо нову емпіричну таблицю.

x

1

xln

2

xln

3

xln

…

n

xln

y

1

yln

2

yln

3

yln

…

n

yln

Із нормальної системи знаходимо

k

і

b

, потім знаходимо

B

і

одержані значення підставляємо в формулу

.Bxy

k

=

Приклад 2. За даною емпіричною таблицею знайти гіперболі-

чну залежність між

x

і

y

:

x

0,5 1 3 5 6

y

0,72 1,05 1,3 1,36 1,42

Розв’язування. Зробивши відповідні позначення, отримаємо

формулу

.bxay

11

+= Складаємо нову розширену емпіричну таб-

лицю для

x і y.

x

2 1 0,33 0,2 0,17 3,7

y

1,39 0,95 0,77 0,73 0,7 4,64

2

x

4 1 0,109 0,04 0,029 5,198

yx

2,78 0,95 0,254 0,146 0,12 4,25

Для знаходження

1

a

і

1

b

розв’язуємо систему рівнянь:

⇔

⎩

⎨

⎧

+−=

=+

⇔

⎪

⎩

⎪

⎨

⎧

=+

.b92,0a74,0b

,25,4b7,3a198,5

.64,4b5a7,3

,25,4b7,3a198,5

11

⎩

⎨

⎧

≈

⇔

⎩

⎨

⎧

+−=

=

.703,0b

,304,0a

.928,0a74,0b

,816,0a68,2

1

11

1

309

Тоді

.31,2

304,0

703,0

a

b

b;29,3

304,0

1

a

1

a

1

≈==≈==

Таким чином отримуємо:

.

x31,21

x29,3

y

+

=

Приклад 3. Задана емпірична таблиця:

x

-1 0 1 2 3

у 0,75 2 5,3 15 40

Знайти зв’язок між

x

і

y

за формулою .Bey

kx

=

Розв

’язування. Згідно з теорією після введення нових позна-

чень залежність між

x

і y матиме такий вигляд:

.bxky +=

Скла-

даємо розширену емпіричну таблицю для

x і y:

x

-1 0 1 2 3 5

y

-0,218 0,693 1,668 2,708 3,689 8,540

2

x

1 0 1 4 9 15

yx

0,218 0 1,668 5,416 11,067 18,39

При складанні таблиці використовуємо формулу

,10lnpxln)10xln(

p

+=⋅ значення

xln

беремо із відповідних ло-

гарифмічних таблиць, а

.3026,210ln = Записуємо нормальну систе-

му рівнянь для знаходження коефіцієнтів прямолінійної залежності:

⎩

⎨

⎧

⎩

⎨

⎧

=

⇔

=

⇔

⎩

⎨

⎧

=+

.723,0b

,985,0k

.708,1b

,85,9k10

.54,8b5k5

,39,18b5k15

За логарифмічними таблицями маємо

.07,2eB

723,0

≈=

Відповідь:

.e07,2y

x985,0

=

Приклад 4. У таблиці задані витрати пального на 100 км

)y( залежно від пробігу автомобіля )x( тис.км.

x

1 5 15 20 30

y

28,3 27,6 22,3 27,4 32,5

Обрати вигляд залежності між

x

і

y

і визначити параметри

цієї залежності.

Розв

’язування. Аналіз показує, що залежність між величинами

x

і

y

параболічна, тобто .cbxaxy

2

++=

310

Виписуємо розширену таблицю:

x

1 5 15 20 30 71

y

28,3 27,6 22,3 27,4 325 138,1

2

x

1 25 225 400 900 1551

3

x

1 125 3375 8000 27000 38501

4

x

1 625 50625 160000 810000 1021251

xy

28,3 138 334,5 548 975 2023,8

yx

2

28,3 690 5017,5 10960 29250 45945,8

Складаємо систему рівнянь:

⎪

⎩

⎪

⎨

⎧

=

−=

=

⇒

⎪

⎩

⎪

⎨

⎧

=++

.54,31c

,15,1b

,04,0a

.1,138c5b71a1551

,8,2023c71b1551a38501

,8,45945c1551b38501a1021251

Таким чином, отримаємо:

54,31x15,1x04,0y

2

+−= .

Шинкарик М.І. Вища математика

Подождите немного. Документ загружается.