Шинкарик М.І. Вища математика
Подождите немного. Документ загружается.


281
З того, що всі границі рівні і співпадають із значенням функції
в точці
)0;0(O , випливає неперервність функції в цій точці.
Аналогічно вводимо поняття границі та неперервності в точці
для функції
).x,...,x,x(fu
n21
=
§4. Частинні похідні функції багатьох змінних.
Геометричний та економічний зміст частинних похідних
4.1. Частинні похідні першого порядку
Розглянемо функцію двох змінних
).y,x(fz = Нехай вона
задана в точці
)y;x(M
000
і в деякому околі цієї точки. Покладемо
,0
yy =
а значенню
0
x надамо приросту
.xΔ
Тоді частинний при-
ріст по
x
матиме вигляд
).y,x(f)y,xx(fz
0000x
−Δ+=Δ
Складемо тепер відношення частинного приросту функції
z
x
Δ до приросту аргументу
xΔ
і знайдемо границю
x
z
lim
x
0x
Δ
Δ
→Δ
. Як-
що така границя існує, то ми назвемо її частинною похідною першо-
го порядку функції
)y,x(fz =
по
x
і позначимо
x
z
′
або
x
z
∂
∂
:
.
x
z
lim
x
)y,x(f
x
)y,x(z
)y,x(z
x
0x
0000
00x
Δ
Δ
=
∂
∂
=
∂
∂
=
′
→Δ
(5.3)
Аналогічно вводиться поняття частинної похідної першого
порядку по
y
. У цьому випадку фіксуємо значення ,xx
0
= а зна-
ченню
,y
0
надаємо приросту
.yΔ
Тоді
)y,x(f)yy,x(fz
0000y
−Δ+=Δ
і відповідно
.
y
z
lim
y
)y,x(f
y
)y,x(z
)y,x(z
y
0y
0000
00y
Δ
Δ
=
∂
∂
=
∂
∂
=
′
→Δ
(5.4)
Із означення частинних похідних випливає таке правило ди-
ференціювання: щоб знайти частинну похідну функції
)y,x(fz =
по
x
, вважаємо
y
постійною величиною, а
x
- змінною. Щоб
знайти частинну похідну по
,
y
вважаємо
x
постійною величи-
ною, а
y
- змінною.
282
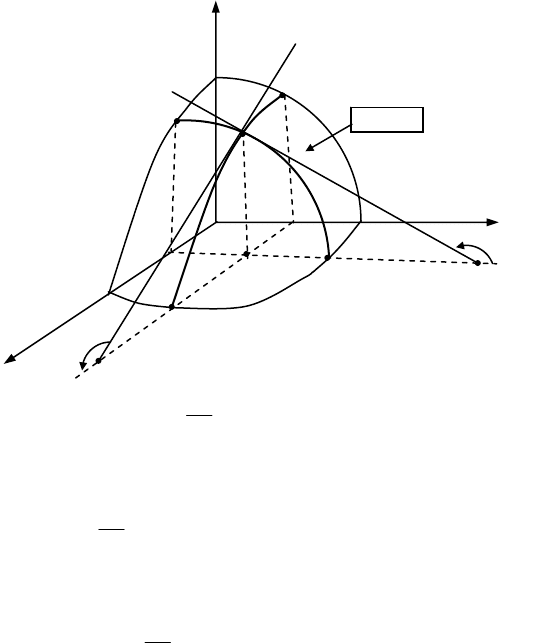
4.2. Геометричний зміст частинних похідних
Частинним похідним першого порядку можна дати гео-
метричну інтерпретацію по аналогії з геометричним змістом
похідної для функції однієї змінної.
Нехай функція )y,x(fz = зображується в просторі де-
якою поверхнею. Спроектуємо точку )z,y,x(M
000
цієї повер-
хні на площину y0x і отримаємо точку )y,x(M
000
(мал.9).
При знаходженні
x
z
∂
∂
покладемо
0
yy = , тоді будемо мати
z=f(x,y
0
). Ця функція однієї змінної має графіком криву AB,
яка розміщена в площині y=y
0
. З геометричної точки зору час-
тинна похідна
x
z
∂
∂
в точці )y,x(M
000
дорівнює
α
tg
(по анало-
гії з функцією однієї змінної), оскільки дотична MS до кривої
AB утворює з віссю Ox кут α.
Таким чином α=
∂
∂
tg)y,x(
x
z
00
Перетнемо тепер поверхню )y,x(fz = площиною
0
xx = . Отримаємо функцію )y,x(fz
0
= , графіком якої є крива
z
O
С
В
D
А
S
x
0
M
0
(x
0
,y
0
)
y
0
T
M(x
0
,y
0
,z
0
)
F
β
α
x
y
Мал
.
9
z=f(x,y)

283
CD
. Тоді дотична
MT
в точці )z,y,x(M
000
до кривої
CD
утворює з віссю y0 кут
β
. Тому
.tg)y,x(
y
z
00
β=
∂
∂
Приклад 1.. Знайти частинні похідні функції .ez
3yx
32
++
=
Розв
’язування. Використовуємо табличну похідну
.ue)e(
uu
′
=
′
.xe2x2e)3yx(ez
3yx3yx
x
323yx
x
323232
++++++
=⋅=
′
++=
′
Аналогічно
.ey3y3e)3yx(ez
3yx223yx
y
323yx
y
222232
++++++
=⋅=
′
++=
′
4.3. Економічний зміст частинних похідних
Відповідним чином можна надати економічного змісту час-
тинним похідним.
Розглянемо в якості прикладу функцію Кобба-Дугласа
βα
⋅= LKAy
Величину
L
y
l =
будемо називати середньою продуктивністю
праці (кількість продукції, виробленої одним робітником).
Величину
K
y
k =
будемо називати середньою фондовіддачею
(кількість продукції, що вироблена одним верстатом).
Величину
L
K
f =
назвемо середньою фондоозброєністю
(фондоозброєність - це вартість фондів, що припадають на одиницю
трудових ресурсів).
Зафіксуємо біжучий стан підприємства, тобто об’єм фондів
K
і число працівників
L
. Їм відповідає випуск продукції
)L,K(yy =
. Якщо найняти ще одного працівника, то приріст випу-
ску продукції
)L,K(y)1L,K(yy −+=Δ
.
А це є частковий приріст функції по
L
і тому L)L,K(yy
L
Δ
′
≈Δ
Оскільки
,1L =Δ
то )L,K(yy
L
′
≈Δ
.

284
Отже, частинна похідна від виробничої функції по об’єму
трудових ресурсів приблизно рівна додатковій вартості продукції,
що вироблена ще одним робітником. Тому похідна
1
L
LKAy
−βα
⋅⋅β=
′
називається граничною продуктивністю праці.
Якщо ж збільшити фонди ще на одиницю – купити ще один
верстат, то додаткова вартість продукції, що вироблена на ньому,
приблизно дорівнює частинній похідній виробничої функції по
об’єму фондів. Тоді
β−α
⋅=
′
LAKLy
1
K
називається граничною фондовіддачею.
І гранична продуктивність праці, і гранична фондовіддача – це
абсолютні величини. Але в економіці надзвичайно цікаво знати на
скільки відсотків зміниться випуск продукції, якщо число робітни-
ків збільшиться на 1%, або якщо фонди зростуть на 1%. Тому розг-
лядаються поняття еластичності випуску продукції по об’єму тру-
дових ресурсів і
еластичності випуску продукції по фондах:
β=β=
′
⋅=
−βα 1
LL
LAK
y
L
y
y
L
)y(E
α=⋅α=
′
⋅=
β−α
LAK
y
K
y
y
K
)y(E
1
kK
Звідси маємо економічний зміст параметрів функції Кобба-
Дугласа.
α
- еластичність випуску по фондах;
β
- еластичність випуску по праці.
Приклад 2. Нехай виробнича функція є функцією Кобба-
Дугласа. Щоб збільшити випуск продукції на 5% треба збільшити
фонди на 10% або чисельність робітників на 15%. В 2001 році один
робітник виготовляв продукцію на 2000 грн., а всього робітників
1000. Основні фонди оцінювались в 4 млн.грн. Записати виробничу
функцію, величину середньої фондовіддачі і середньої
продуктив-
ності праці.
Розв
’язування. Зрозуміло, що еластичність випуску продукції
по праці
3
1
=β
, а по фондах
2
1
=α
. Отже, функція Кобба-Дугласа

285
має вид
3
1
2
1
LKAy ⋅= , 1
6
5
3
1
2
1
<=+
. Підставляючи інші величини,
отримаємо:
3
1
2
1
6
)1000()104(A10002000 ⋅⋅⋅=⋅
, тобто
,10102A10002000
3
⋅⋅⋅=⋅ 100
10
2000
10002000
A =
⋅
⋅
=
.
Отже, виробнича функція
.LK100y
3
1
2
1
⋅= Середня фондовід-
дача рівна
2
1
4000000
10002000
K
y
k =
⋅
==
, а середня продуктивність
.2000
1000
10002000
L
y
l =
⋅
==
4.4. Частинні похідні функції багатьох змінних
Ми розглянули випадок функції двох змінних. Для функції
)x,...,x,x(fu
n21
= означення частинних похідних вводиться ана-
логічно і знаходиться
n
частинних похідних:
.
x
u
,...,
x
u
,
x
u
n21
∂
∂
∂
∂
∂
∂
Очевидно, що для функцій багатьох змінних можна викорис-
товувати відомі правила диференціювання, включаючи таблиці по-
хідних, які отримані для функцій однієї змінної.
§5. Градієнт функції багатьох змінних.
Похідна функції по напрямку
5.1. Градієнт функції багатьох змінних
Означення 5. Градієнтом функції )y,x(fz = називається
вектор
jzizqradz
yx
⋅
′
+⋅
′
= (5,5)
Аналогічно для функції
)z,y,x(fu =
kujuiuqradu
zyx
⋅
′
+⋅
′
+⋅
′
=
(5.6)
Відповідно вводимо градієнт функції
)x,...,x,x(fu
n21
=

286
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
∂
∂
∂
∂
=
n21
x
u
;...;
x
u
;
x
u
qradu
. (5.7)
Скорочено градієнт функції позначимо через
→
q .
5.2. Похідна складної функції
Відомо, що для похідної складної функції однієї змінної
),u(fy =
де
),x(uu =
має місце формула
u)u(fy
u
′
⋅
′
=
′
.
Узагальнимо цю формулу на випадок функції двох змінних
).y,x(fz = Нехай задана диференційовна функція )y,x(fz = , яка
має неперервні частинні похідні
x
z
′
і
y
z
′
. Допустимо , що аргументи
x
і
y
є в свою чергу диференційовними функціями від третьої змін-
ної
:
t
);t(x
ϕ
= ).t(y
ψ
= Ясно, що функція )y,x(fz = є
складною функцією від змінної
t
: )t(F))t(),t((fz =
ψ
ϕ
= .
Знайдемо похідну цієї функції по змінній
t
. Для цього надамо
приросту
tΔ аргументу
t
і знайдемо повний приріст функції zΔ ,
якщо аргументи
x
і
y
набувають відповідно приростів
xΔ
і
yΔ
:
)y,x(f)yy,xx(fz −Δ+Δ+=Δ .
Перепишемо цей приріст в іншому вигляді:
[][]
)y,x(f)yy,x(f)yy,x(f)yy,xx(fz −Δ++Δ+−Δ+Δ+=Δ
.
Застосуємо тепер теорему Лагранжа про скінчені прирости ві-
дповідно до першої і другої квадратних дужок. Тоді отримаємо:
y)yy,x(fx)yy,xx(fz
2y1x
ΔΔθ+
′
+ΔΔ+Δθ+
′
=Δ
.
Допустимо тепер, що частинні похідні неперервні по сукупно-
сті змінних
x
і
y
, тоді:
,)y,x(f)yy,xx(f
1x1x
ε+
′
=Δ+Δθ+
′
.)y,x(f)yy,x(f
2y2y
ε+
′
=Δθ+
′
Таким чином,
yxy)y,x(fx)y,x(fz
21yx
Δε+Δε+Δ
′
+Δ
′
=Δ .
Тепер згідно означення похідної знаходимо:
t
y
t
x
t
y
y
z
t
x
x
z
t
z
21
Δ
Δ
ε+
Δ
Δ
ε+
Δ
Δ
⋅
∂
∂
+
Δ
Δ
⋅
∂
∂
=
Δ
Δ
.

287
Перейшовши до границі при 0t →Δ і враховуючи, що
0limlim
2
0t
1
0t
=ε=ε
→Δ→Δ
, отримаємо формулу:
dt
dy
y
z
dt
dx
x
z
dt
dz
⋅
∂
∂
+⋅
∂
∂
=
.
Ця похідна називається повною похідною функції
)y,x(fz =
по аргументу
t
. Аналогічно вводиться формула повної похідної для
функції
)z,y,x(uu =
t
z
z
u
dt
dy
y
u
dt
dx
x
u
dt
du
∂
∂
⋅
∂
∂
+⋅
∂
∂
+⋅
∂
∂
=
,
де
),t()t(x
1
ϕ
=
),t()t(y
2
ϕ
=
)t()t(z
3
ϕ
=
.
Поняття похідної функції
)y,x(fz = можна узагальнити,
якщо ввести похідну функції по напрямку.
5.3. Похідна функції по напрямку
Нехай функція
)y,x(fz =
задана в деякій замкнутій області
D
площини y0x .
Нехай в цій області задана точка
)y,x(M
000
. Надамо прирос-
ту аргументам відповідно
xΔ і yΔ , тоді отримаємо точку
)yy,xx(M
00
Δ+Δ+ . Розглянемо вектор
→→→
⋅Δ+⋅Δ= jyixMM
0
.
Позначимо через
ϕ
кут, який утворює вектор
→
MM
0
з віссю
x0
, а через
l
- довжину цього вектора. Тоді можна записати:
,coslx
ϕ
=Δ
ϕ
=Δ sinly або ,cosldx
ϕ
= .sinldy
ϕ
=
Таким чином:
.jsinlicoslMM
0
→→→
ϕ+⋅ϕ= Значення функції
)y,x(fz = в точках
0
M і
M
відповідно будуть такі:
)y,x(f
00
і
)sinly,coslx(f
00
ϕ
+
ϕ
+
.
Звідси випливає, що коли зафіксувати точку
0
M і напрямок
вектора
→
MM
0
і міняти тільки l , то функцію
)y,x(fz =
можна за-
писати у вигляді
)l(Fz = , а її значення в точках
0
M і
M
відповідно
)0(F і ).l(F Таким чином
).sinly,coslx(f)l(F
00
ϕ
+
ϕ
+=
288
Згідно означення похідної функції однієї змінної, похідна фу-
нкції
)l(Fz =
по змінній
l
дорівнює
l
z
lim
0
l
)0(F)l(F
lim
dl
dz
0l0l
Δ
Δ
=
−
−
=
→Δ→
.
Цю границю назвемо похідною функції
)y,x(fz =
по дано-
му напрямку. Виходячи із викладеного вище, функцію
)y,x(fz =
можна вважати складною функцією по
l
. Її повна похідна по
l
до-
рівнює
dl
dy
y
z
dl
dx
x
z
dl
dz
⋅
∂
∂
+⋅
∂
∂
=
.
Але
,cosldx
ϕ
=
ϕ
= sinldy
, тому
.sin
y
z
сos
x
z
dl
dz
ϕ
∂
∂
+ϕ
∂
∂
=
Цю формулу можна узагальнити на випадок функції трьох
змінних
)t,y,x(fu =
. В цьому випадку напрямок задається векто-
ром
)cos,cos,(cosn γβα
→
і формула диференціювання по напрямку
відповідно матиме вид
γ
∂
∂
+β
∂
∂
+α
∂
∂
= cos
z
u
cos
y
u
cos
x
u
dl
du
.
Встановимо зв’язок між похідною функції
)y,x(fz =
по на-
прямку і градієнтом цієї функції. Для цього розглянемо вектори
→→→
⋅
∂
∂
+⋅
∂
∂
== j
y
z
i
x
z
qradzq
і
→→→
ϕ+ϕ= jsinicosa .
Помножимо скалярно вектор
→
q на вектор
→
a , отримаємо:
ϕ
∂
∂
+ϕ
∂
∂
=⋅
→→
sin
y
z
cos
x
z
)aq(
. Таким чином ,
)aq()aqradz(
dl
dz
→→→
⋅=⋅= . Згідно з означенням скалярного до-
бутку
α⋅⋅
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=α⋅⋅=
→→
cos1
y
z
x
z
cosaq
dl
dz
2
2
.
Із цієї формули випливає, що у випадку, коли напрямок век-
тора
→
a
співпадає з напрямком вектора )1(cosq =α
→
289
2
2
max
y
z
x
z
q
dl
dz
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
==
⎟
⎠
⎞
⎜
⎝
⎛
→
.
Висновок. Похідна функції
z=f(x,y) має найбільше значення по
напрямку градієнта
→
q і дорівнює модулю градієнта
→
q .
Приклад 3. Обчислити градієнт функції
22
yxz +=
в точці
M
0
(3,4).
Розв
’язування. Знаходимо частинні похідні функції
2222
yx
x
yx2
x2
x
z
+
=
+
=
∂
∂
; .
yx
y
yx2
y2
y
z
2222
+
=
+
=
∂
∂
Обчислимо їх значення в даній точці:
5
3
x
)M(z
0
=
∂
∂
;
5
4
y
)M(z
0
=
∂
∂
.
Таким чином
,j
5
4
i
5
3
qradzq
→→→
⋅+⋅== .1
25
16
25
9
q =+=
→
§ 6. Повний приріст та повний диференціал функції
багатьох змінних
Нехай z=f(x,y) - функція двох змінних. Надамо обом змінним
прирости відповідно Δx і Δy, тоді функція z отримає приріст
),y,x(f)yy;xx(fz −Δ+Δ+=Δ який називається повним приро-
стом функції.
Відомо, що для функції y=φ(x), яка має похідну )x(y
ϕ
′
=
′
,
приріст функції можна зобразити у вигляді
,xx)x(y Δε+Δ⋅
ϕ
′
=Δ
(5.8)
де ε→
0, якщо Δx→0.
Тоді головна лінійна частина приросту функції називаєть-
ся диференціалом функції dy=φ′(x)Δx= φ′(x)dx.
В випадку функції двох або більше змінних наявність ча-
стинних похідних ще не гарантує того, що повний приріст фу-
нкції можна представити в виді, аналогічному (5.8).
Означення 6 .Функція z=f(x,y) називається диференційов-
ною в даній точці ),y;x(M якщо її повний приріст в цій точці
можна представити в виді:

290
,yxyBxAz
21
Δ⋅ε+Δ⋅ε+Δ⋅+Δ⋅=Δ
(5.9)
де
0,0
21
→ε→ε при ,0y,0x →Δ→Δ а
A
і
B
не залежать від
приростів .y,x ΔΔ
Доданки
x
1
Δε і y
2
Δε є, очевидно, нескінченно малими вели-
чинами вищого порядку малості, ніж
xΔ і .yΔ
Означення 7. Повним диференціалом функції
)y;x(fz =
називається головна лінійна частина приросту функції відносно
xΔ і yΔ , тобто: yBxAdz Δ⋅+Δ⋅= або .BdyAdxdz +=
ТЕОРЕМА 1. Якщо функція
)y;x(fz =
диференційовна в
даній точці
)y;x(M , то існують частинні похідні цієї функції і
має місце рівність
,zB;zA
yx
′
=
′
=
тобто
dyzdxzdz
yx
′
+
′
=
. (5.10)
Доведення
. Нехай функція )y,x(fz = диференційовна. Тоді
має місце формула (5.9). Покладемо
:0y =Δ
тоді із (5.9) отримаємо
xxAz
1x
Δε+Δ=Δ
звідки
1
x
A
x
z
ε+=
Δ
Δ
, де
,0
1
→ε
якщо .0x →Δ
Оскільки
A
- стала величина (
x
і
y
фіксовані), то
.Az
x
z
lim
x
x
0x
=
′
=
Δ
Δ
→Δ
Аналогічно доводиться, що
.Bz
y
=
′
Таким чином, формула
(5.10) доведена.
Нехай задана функція
).x,...,x,x(fu
n21
=
Можна довести, по
аналогії з функцією
),y,x(fz = що в випадку диференційовності
функції
)x,...,x,x(fz
n21
=
має місце формула
nx2x1x
dxu...dxudxudu
n21
′
++
′
+
′
=
(5.11)
Навпаки, якщо допустити , що функція
)x,...,xx(fu
n21
=
має
частинні похідні, які є неперервними функціями по сукупності
змінних в околі точки
M(x
1
,x
2
,…,x
n
) то справедлива формула (5.11).
§7. Частинні похідні вищих порядків
Оскільки частинні похідні першого порядку функції
)y,x(fz = знову є функціями від
x
і
y
, то від них можна ще раз
