Шинкарик М.І. Вища математика
Подождите немного. Документ загружается.

251
Тоді існують такі
значення функції
),x(f які в порівнянні
з іншими сусідніми зна-
ченнями є найбільшими
чи найменшими. Такі
значення називають ві-
дповідно максимумами
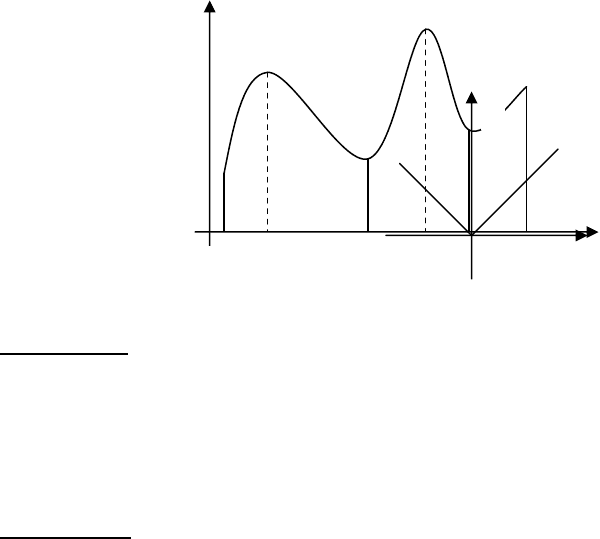
і мінімумами. На малю-
нку 9
),x(f
1
−)x(f
3
максимуми,
−)x(f),x(f
42
мінімуми.
Означення 1. Максимумом функції )x(f називається таке
значення ),x(f
0
яке не менше всіх значень функції в точках дос-
татньо близьких до
.x
0
При цьому виконується нерівність
)x(f)xx(f
00
≤Δ+
для будь-яких достатньо малих xΔ .
Точка
0
x , в якій функція )x(f досягає максимуму )x(f
0
,
називається точкою максимуму.
Означення 2. Мінімумом функції )x(f називається таке
значення
),x(f
0
яке не більше всіх значень функції в точках до-
статньо близьких до
.x
0
При цьому маємо
)x(f)xx(f
00
≥Δ+
для будь-яких достатньо малих .xΔ
Точка
0
x , в якій функція )x(f досягає мінімуму )x(f
0
,
називається точкою мінімуму.
Максимуми і мінімуми разом називають екстремумами. Фун-
кція може мати всередині інтервалу
()
b,a декілька екстремумів.
15.2 Необхідні умови екстремуму
Для відшукання екстремумів розглянемо спочатку не-
обхідні умови екстремуму.
ТЕОРЕМА.
(необхідна умова екстремуму).
Якщо функція )x(f має в точці
0
x екстремум, то її похі-
дна в цій точці дорівнює нулю, або не існує.
Доведення
. Нехай в точці
0
x функція )x(f має похідну і
досягає максимуму. Це означає, що при достатньо малому
хΔ
x
1
Мал.9
у=f(х)
x
O
a
b
y
x
3
x
4
x
2
у
х
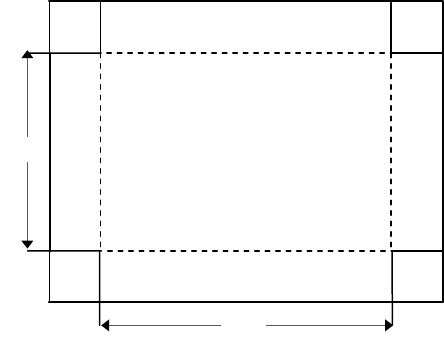
О
Мал.3

252
маємо
).x(f)xx(f
00
≤Δ+
З цього випливає, що відношення
,0
x
)x(f)xx(f
00
≥
Δ
−Δ+
якщо
0x <Δ
і
,0
x
)x(f)xx(f
00
≤
Δ
−Δ+
якщо
.0x >Δ Переходячи в нерівностях до границі, дістанемо
0)x('f
0
≥
і
.0)x('f
0
≤
А це може одночасно виконуватись тільки при
.0)x('f
0
=
Аналогічно доводиться перша частина теореми у випадку, ко-
ли функція
)x(f досягає в точці
0
x мінімуму.
Але неперервна функція
)x(f може мати екстремум в точ-
ках, в яких похідна не існує. Наприклад, функція
xy = в точці
0x = не диференційована, але досягає в ній мінімуму, що видно з
графіка (мал.3).
Такі точки називають кутовими. Але ці умови не є достатніми.
Похідна може дорівнювати нулю не тільки в точках екстремуму.
Так похідна функції
3
xy = є
2
x3'y = . В точці 0x = ,0'y = але в
цій точці функція не досягає екстремального значення.
Точки, в яких похідна функціі дорівнює нулю або не існує на-
зивають стаціонарними або критичними точками першого роду.
15.3. Достатні умови екстремуму
ТЕОРЕМА
(перше правило). Якщо похідна функції )x('f
при переході через критичну точку
0
x зліва направо змінює
знак з “+”на “-“, то
)x(f має максимум в точці
0
x , якщо зміна
знаку відбувається з “-“ на “+”, то функція має мінімум в цій
точці. Відсутність зміни знаку вказує на відсутність екстремуму.
Доведення
. Якщо похідна )x('f при переході через точку
0
xx =
змінює знак з “+”на “-“, то це означає, що при досить мало-
му
хΔ похідна
)x('f
додатня на проміжку
)x,xx(
00
Δ−
і
від’ємна на проміжку
).xx,x(
00
Δ+ Отже, функція )x(f зростає
на проміжку
)x,xx(
00
Δ− і спадає на проміжку )xx,x(
0
0
Δ+ , тоб-
то в точці
0
x
досягає максимуму.
Аналогічно доводиться твердження теореми відносно
мінімуму функції.

253
ТЕОРЕМА.(друге правило). Якщо в точці x
0
перша похідна
f
′(x) функції f(x) дорівнює нулю, а її друга похідна f″(x) непере-
рвна в околі цієї точки і
f″(x)≠0, то функція f(x) має максимум в
точці
x
0
, коли
0)x(''f
0
<
і мінімум , коли
.0)x(''f
0
>
Доведення
. Нехай 0)x('f
0
= і .0)x(''f
0
> Тоді внаслідок
неперервності
)x(''f
вона додатня в малому інтервалі
).хx,xx(
00
Δ+Δ− Це означає, що )x('f , для якої )x(''f є похід-
ною, зростає в цьому інтервалі. Оскільки
0)x('f
0
=
, то на проміж-
ку
)x,xx(
00
Δ−
похідна
,0)x('f <
а на проміжку
)xx,x(
00
Δ+
похідна
.0)x('f >
Тому
)x(f
в інтервалі
)x,xx(
00
Δ−
спадає, а в інтервалі
)xx,x(
00
Δ+
зростає. Значить, в точці
0
x
функція
)x(f
має міні-
мум.
Аналогічно доводиться достатність умови існування
максимуму.
Зауваження
. Треба мати на увазі, що другим правилом не мо-
жна користуватися у випадку,коли критична точка
0
x
одержана від
того, що в ній похідна не існує, а також, якщо
.0)x(''f
0
=
Тоді ко-
ристуються першим правилом.
Приклад.
Знайти максимум і мінімум функції
.1x3x2x
3
1
y
23
++−=
Розв
’язування.Дана функція визначена на проміжку
).,( ∞−∞
Знаходимо похідну і прирівнюємо її до нуля.
.03x4x
,3x4x'y
2
2
=+−
+−=
Корені даного рівняння
.3x,1x
21
==
Спочатку використаємо перше правило
).3x)(1x('y −−=
Область визначення функції критичними точками ділиться на
проміжки:
),3()3,1()1,( ∞∪∪−∞ (мал.10). Знайдемо знаки
похідної в кожному з цих проміжків, підставивши конкретні числа з
них в похідну.
+
-
+
Мал
.10
1
3

254
Наприклад ,
.03)34)(14()4('y
,01)32)(12()2('y
,03)30)(10()0('y
>=−−=
<−=−−=
>=−−=
Отже, в точці −= 1x макси-
мум.
.
3
1
2113121
3
1
y
23
max
=+⋅+⋅−⋅=
В точці
−= 3x мінімум. .1133323
3
1
y
22
min
=+⋅+⋅−⋅=
При застосуванні другого правила знаходимо другу похідну
.4x2''y −=
Підставляємо значення
1x
1
= і 3x
2
= в другу похідну:
02412)1(''y <−=−⋅= , .02432)3(''y >=−⋅=
В точці
−= 1x
1
максимум , в точці −= 3x
2
мінімум.
§16. Найменше та найбільше значення функції на відрізку
За теоремою Вейєрштраса неперервна функція на замкнутому
відрізку
[]
b,a досягає свого найбільшого і найменшого значення. Ці
значення функція може досягти на одному з кінців відрізка або все-
редині відрізка. Тому задачу знаходження найбільшого і найменшо-
го значень функції на відрізку
[]
b,a розв’язують так:
1). Знаходять похідну, і прирівнявши її до нуля, знаходять
критичні точки першого роду.
2). Обчислюють значення функції в усіх критичних точках,
що належать проміжку
[]
b,a і значення функції на кінцях відрізка.
3). Серед цих значень вибирають найбільше і найменше зна-
чення.
Зауваження
. Якщо всередині проміжку функція має тільки
одну критичну точку і досягає в ній максимуму, то він буде найбі-
льшим значенням, а якщо досягає в ній мінімуму, то він буде най-
меншим значенням.
Приклад. Знайти найбільше і найменше значення функції
3x12x3x2y
23
+−−=
на проміжку
[]
1,2−
.
Розв
’язування. Знаходимо похідну .12x6x6y
2
−−=
′
255
Прирівнявши похідну до нуля, знаходимо критичні точки
першого роду:
012x6x6
2
=−− ,
.2x;1x
,02xx
21
2
=−=
=−−
Оскільки точка
2x
2
=
не входить в даний проміжок, її до
уваги не беремо. Обчислюємо значення функції:
.103123231121312)1(y
;10312323)1(12)1(3)1(2)1(y
;132412163)2(12)2(3)2(2)2(y
23
23
23
−=+−−=+⋅−⋅−⋅=
=++−−=+−−−−−=−
−=++−−=+−−−−−=−
Отже, найбільше значення функції 10y = в точці
,1x −=
а най-
менше значення
10y −= в точці .1x =
§17. Приклади задач оптимізації з економічним змістом
Задача 1. На підприємстві з відходів бляшаних листів прямо-
кутної форми розмірами
дм5дм8 ×
вирішили виготовляти відкриті
зверху ящики найбі-
льшого об’єму, вирі-
завши по кутах рівні
квадратики і загну-
вши бляху, щоб
отримати бічні стін-
ки. Якої довжини
мають бути сторони
вирізаних квадратів?
Розв
’язування.
Нехай
x
сторони
вирізаних квадратів
(мал.11).
Тоді розміри
ящика будуть
,x28−
x25−
і
.
x
Об’єм ящика
8
-
х
х
х
х
5
-
Мал.1
1

256
)x28)(x25(xV −−= . Знайдемо найбільше значення цієї функції при
умові , що
5,2x0 << . .x40x26x4V
23
+−= Обчислимо похідну
.40x52x12V
2
+−=
′
Прирівнявши її до нуля, знайдемо критичні точки першого
роду:
010x13x3,040x52x12
22
=+−=+−
,
49120169103413D
2
=−=⋅⋅−= ,
.
3
10
6
713
x,1
6
713
x
21
=
+
==
−
=
Оскільки точка
5,2
3
10
x
2
>= не входить у вказаний промі-
жок, то вона відкидається.
Знайдемо другу похідну
V
′′
;52x24V −=
′′
0285224)1(V <−=−=
′′
.
Отже, в точці
1x = функція V досягає максимуму. При
0x = і
5,2x =
, 0V = .
Відповідь:
.найб
V
досягається при
)дм(1x =
.
Задача 2. Треба виготовити відкритий циліндричний бак
об’єму
V . Матеріал, з якого виготовляють дно бака коштує
1
p
гри-
вень за
,м
2
а вартість матеріалу бокової поверхні -
2
p
гривень за
.м
2
При якому співвідношенні радіуса дна до висоти витрати на ма-
теріал будуть найменшими?
Розв
’язування. Нехай
r
радіус основи, а
h
висота бака. Тоді
об’єм бака
hrV
2
π= , а витрати на матеріал
21
2
rhp2prZ π+π= .
Виразимо з формули об’єму
2
r
V
h
π
=
і підставимо у вираз для
Z. Одержимо функцію однієї змінної
r
Vp2
pr
r
rVp2
prZ
2
1
2
2
2
1
2
+π=
π
π
+π=
. Знайдемо похідну
2
2
1
r
Vp2
rp2Z −π=
′
.
Знаходимо критичні точки:
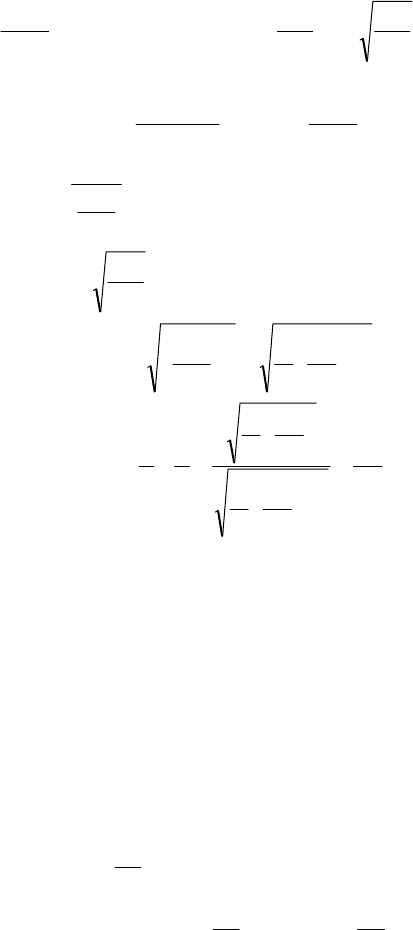
257
0
r
Vp2
rp2
2
2
1
=−π , ;Vppr
21
3
=π ,
p
Vp
r;
p
Vp
r
3
1
2
1
2
3
π
=
π
=
друга точка
0r = не входить в область визначення функції.
Знайдемо
;
r
Vp4
p2
r
r2Vp2
p2Z
3
2
1
4
2
1
+π=
⋅
+π=
′′
.0p6p4p2
p
Vp
Vp4
p2)r(Z
111
1
2
2
1
>π=π+π=
π
+π=
′′
Отже, в точці
3
1
2
p
Vp
r
π
=
функція витрат
Z
має мінімум.
Знаходимо
h:
3
2
1
2
3
2
1
2
p
pV
p
Vp
:Vh
−
⎟
⎠
⎞
⎜
⎝
⎛
π
=
⎟
⎠
⎞
⎜
⎝
⎛
π
π=
.
Знайдемо відношення
h
r
:
1
2
3
2
1
2
3
1
2
p
p
p
pV
p
pV
h
r
=
⎟
⎠
⎞
⎜
⎝
⎛
π
⎟
⎠
⎞
⎜
⎝
⎛
π
=
−
.
Отже, радіус дна до висоти бака повинен відноситись як ціна
матеріалу дна до ціни матеріалу бокової поверхні.
Задача 3. Фірма вирішила випускати нові радіоприймачі.
Економічним підрозділом фірми встановлено, що при випуску
x
приймачів щоквартально затрати будуть
x3090000)x(V += (гри-
вень), а кількість проданих приймачів в залежності від ціни
p
(гри-
вень) за один приймач становитиме
.p309000x −= При якому ви-
пуску фірма матиме найбільший дохід і прибуток? Який найбіль-
ший дохід і прибуток, і при якій ціні, якщо фірма щоквартально мо-
же випускати до 5000 приймачів?
Розв
’язування. Знайдемо ціну р:
.
30
x
300p;x9000p30 −=−=
Тоді дохід від реалізації
радіоприймачів
.
30
x
x300x)
30
x
300(px)x(D
2
−=−==

258
Знайдемо маржинальний дохід і, прирівнявши його до нуля,
знайдемо критичні точки:
;
15
x
300
30
x2
300)x(D −=−=
′
;0
15
x
300 =−
4500x =
.
Оскільки
,0
15
1
)x(D <−=
′′
а точка 4500x = єдина входить в
даний проміжок [
0;5000], то в цій точці D(x) досягає найбільшого
значення.
675000
30
)4500(
4500300)4500(DD
2
max
=−⋅==
(гривень).
Досягається це значення доходу при ціні на приймач
150
30
4500
300p =−= (гривень).
Прибуток
)x(P шукаємо як різницю між доходом )x(D
і витратами
)x(V
:
).x(V)x(D)x(P −=
.90000
30
x
x27090000x30
30
x
x300)x(P
22
−−=−−−=
Знаходимо маржинальний прибуток і, прирівнявши його до
нуля, критичні точки:
15
x
270
30
x2
270)x(P −=−=
′
; 0
15
x
270 =−
; 4050x = .
Оскільки
15
1
)x(P −=
′′
, а точка
4050x =
єдина входить в промі-
жок [
0;5000], то в цій точці P(x) досягає найбільшого значення.
45675090000
30
)4050(
4050270)4050(PP
2
max
=−−⋅== (гривень).
З формули прибутку видно, що максимальний прибуток дося-
гається, якщо
)x(V)x(D
′
=
′
, тобто коли маржинальні витрати до-
рівнюють маржинальному доходу.
Максимальний прибуток досягається при випуску і продажі
4050 приймачів по ціні
165
30
4050
300
р =−=
(гривень).
Отже, максимальна виручка (дохід)
675000грн. досягається
при випуску і реалізації
4500 радіоприймачів по ціні 150 грн. за
приймач, а максимальний прибуток
456750 грн. при випуску і реалі-
зації
4050 радіоприймачів по ціні 165 грн. за приймач.
259
§18.Опуклість і вгнутість графіка функції.
Точки перегину
При дослідженні функцій з метою побудови їх графіків важ-
ливу роль відіграють такі поняття як опуклість і вгнутість кривих.
Означення 1. Крива
)x(fy =
називається опуклою в точці
0
x , якщо в околі цієї точки крива знаходиться під
дотичною до кривої, проведеної в цій точці (мал.12).
Означення 2. Крива )x(fy = називається вгнутою в точці
0
x
, якщо в околі цієї точки крива знаходиться над дотичною до
кривої, проведеної в цій точці (мал 13).
Означення 3. Крива
)x(fy =
називається опуклою (вгну-
тою) на проміжку ),b,a( якщо вона опукла (вгнута) в кожній
точці цього проміжку.
Для встановлення проміжків, на яких графік функції
)x(fy = опуклий, а на яких вгнутий, вкажемо теорему, яка дає
достатні умови опуклості і вгнутості кривих на проміжку.
ТЕОРЕМА.
Якщо на проміжку
)b,a(
друга похідна функ-
ції
)x(fy = від’ємна, то її графік опуклий на цьому проміжку,
якщо
)x(''f
додатня на
)b,a(
, то графік
)x(fy =
вгнутий.
Не приводячи строгого доведення, приведемо геометричні
міркування, які пояснюють теорему.
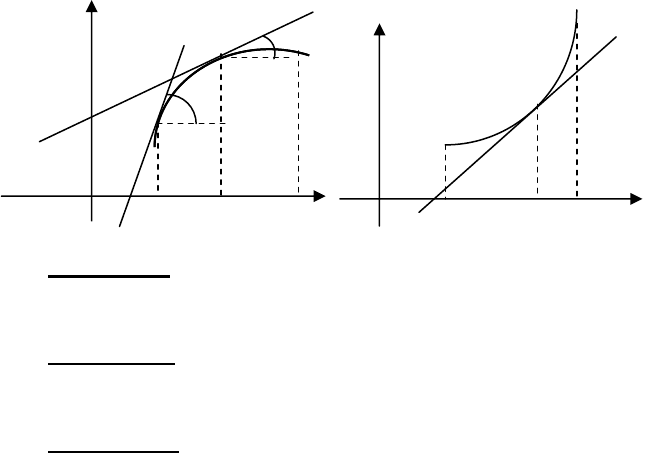
Якщо скрізь на проміжку
(a,b) f″(x)<0, то це означає, що f′(x),
як функція для якої
f″(x) є похідною, буде спадною. Отже, спадає на
розглядуваному проміжку кутовий коефіцієнт дотичної
tgα до кри-
вої і спадає сам кут α, утворюваний дотичною з додатним напрямом
осі
Ox (мал12).
x
O
у
b
у
x
x
0
O
а
Мал.1
2
Мал.1
3
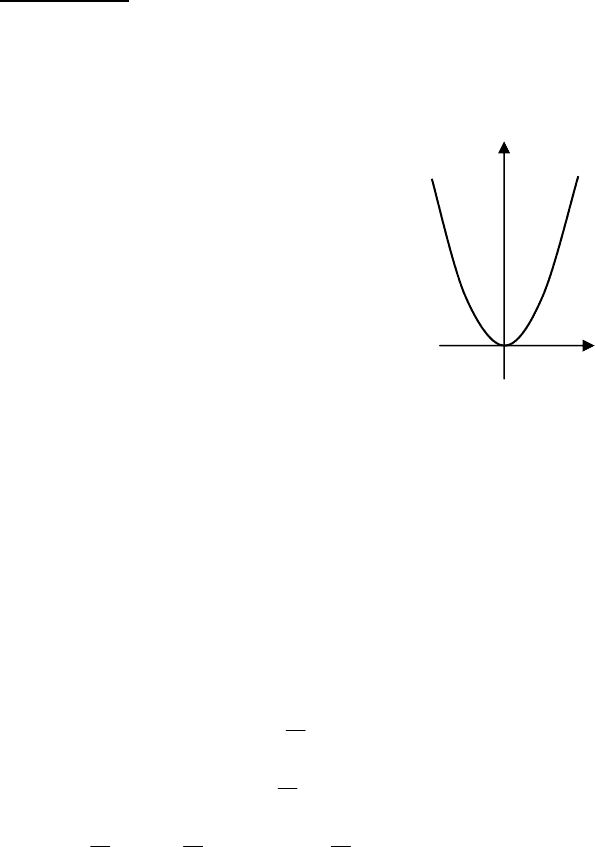
260
Очевидно крива на проміжку
)b,a(
розташована під дотич-
ною. Якщо
,0)x(''f > то крива буде угнутою.
Означення 4. Точка, яка відокремлює опуклу частину непе-
рервної кривої від вгнутої чи навпаки, називається точкою пере-
гину.
Необхідні умови існування точки перегину дає теорема.
ТЕОРЕМА. Якщо
0
x
- точка перегину неперервної функ-
ції
)x(fy =
, то друга похідна її
)x(''f
в цій точці
дорівнює нулю або не існує.
Точки, в яких
)x(''f дорівнює нулю
або не існує називають критичними точками
другого роду.
Проте умови теореми не є достатніми.
Так для функції
4
xy =
друга похідна
2
x12''y =
дорівнює нулю при .0x = Проте
графік її вгнутий в цій точці (мал.14).
◙ Достатні умови існування точки перегину.
ТЕОРЕМА. Якщо друга похідна
)x(''f
в точці
0
x
дорів-
нює нулю і міняє знак при переході через цю точку, то точка з
абсцисою
0
x
є точкою перегину кривої
)x(fy =
.
Доведення
. Припустимо, що в точці М з абсцисою
0
xx = ,
друга похідна
0)x(''f = і при переході через неї зліва на право
змінює знак з мінуса на плюс. Тоді зліва від
М крива опукла
(
),0)x(''f <
а справа крива вгнута
).0)x(''f( >
Отже, в точці М
крива змінює опуклість на вгнутість, і тому точка
М є точкою пере-
гину.
Приклад
. Знайти точки перегину і визначити проміжки
опуклості та вгнутості кривої
2
x
2
ey
−
=
(крива Гаусса).
Знаходимо похідні:
,xe'y
2
x
2
−
−=
.e)1x(exe''y
2
x
2
2
x
2
2
x
222
−−−
−=+−=
Прирівнюємо другу похідну до нуля і знаходимо критичні
Мал
.1
х
О
у
