Шинкарик М.І. Вища математика
Подождите немного. Документ загружается.

231
Приклад. Знайти похідну функції
y
заданої параметрично
⎩
⎨
⎧
=
=
tsinby
tcosax
.
Розв
’язування. Знаходимо
t
x
′
і
t
y
′
: tsinax
t
−=
′
, .tcosby
t
=
′
Тоді
ctgt
a
b
t
sin
a
tcosb
y
x
−=−=
′
.
§8. Похідні деяких елементарних функцій
8.1. Похідна логарифмічної функції
Нехай
xlogy
a
= ,0a( > )1a ≠ .Знайдемо її похідну, корис-
туючись означенням. Надамо аргументу
х приріст 0x ≠Δ такий, що
.0xx >Δ+ Знаходимо приріст функції yΔ :
)
x
x
1(log)
x
xx
(logxlog)xx(logy
aaaa
Δ
+=
Δ+
=−Δ+=Δ
.
Складемо відношення приростів
)
x
x
1(log
x
1
x
y
a
Δ
+
Δ
=
Δ
Δ
.
Обчислюємо границю цього відношення при
0→Δx
, ввівши
заміну
α=
Δ
x
x
.
=α+
α
=
Δ
+
Δ
=
Δ
Δ
=
→α→Δ→Δ
)1(log
1
x
1
lim)
x
x
1(log
x
1
lim
x
y
lim'y
a
0
a
0x0x
.
alnx
1
elog
x
1
)1(limlog
x
1
a
1
0
a
==α+=
α
→α
При цьому ми використали неперервність логарифмічної фун-
кції і другу визначну границю.
При
а = е маємо
.
x
1
)'x(ln =
8.2. Похідна від показникової функції
Нехай
).1a,0a(ay
x
≠>=
Знайти
y
′
.
Прологарифмуємо обидві частини цієї рівності при основі е:
alnxyln =
. Продиференціюємо обидві частини одержаної рівності,
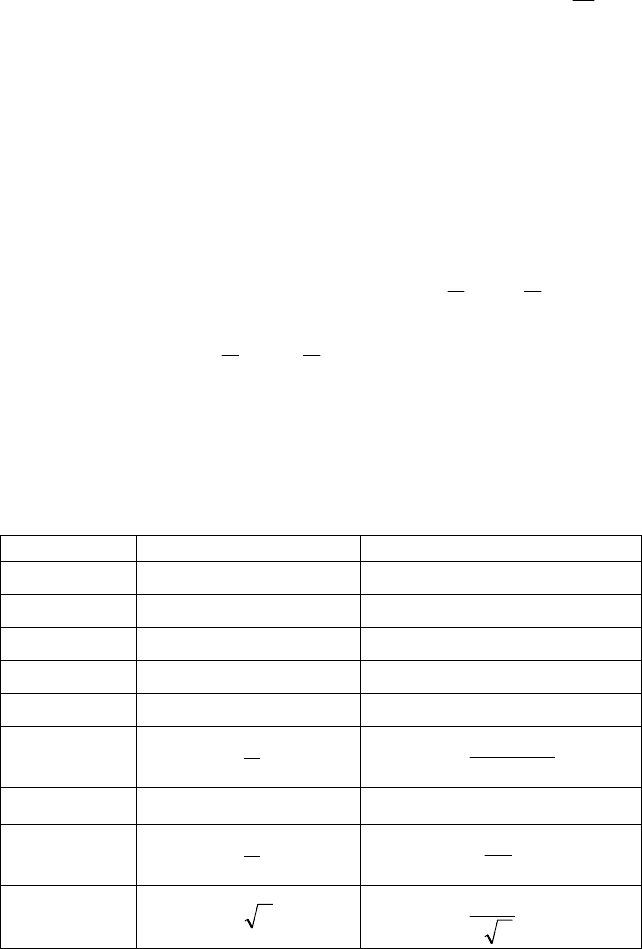
232
використавши правило диференціювання неявної функції:
aln
y
'y
=
.
Звідси,
.alnaalny'y
x
==
Якщо
а = е, то
xx
e)'e( =
.
8.3. Похідна степеневої функції
Нехай
,xy
α
= де
α
- довільне дійсне число. Функція
α
= xy визначена для довільних
α
при 0x > . Тому її можна
прологарифмувати
xlnyln α= . Використавши правило
диференціювання неявної функції, одержимо
x
1
y
y
1
α=
′
.
Звідси,
1
x
x
1
x
x
1
yy
−αα
α=α=⋅α=
′
.
§9. Таблиця похідних
Враховуючи правила диференціювання , встановлені формули
похідних і узагальнивши їх на складні функції, складемо таблицю
основних формул диференціювання.
№ /п Функція Похідна
І y = C
y
′
= 0
II y = x
y
′
= 1
III y = Cu
uCy
′
=
′
IV y = u± v
vuy
′
±
′
=
′
V y = uv
uvvuy
′
+
′
=
′
VI
v
u
y =
2
v
u'vv'u
'y
−
=
VII
n
uy = 'unuy
1n−
=
′
VIIa)
u
1
y =
2
u
'u
'y −=
VIIб)
uy =
u2
'u
'y =
233
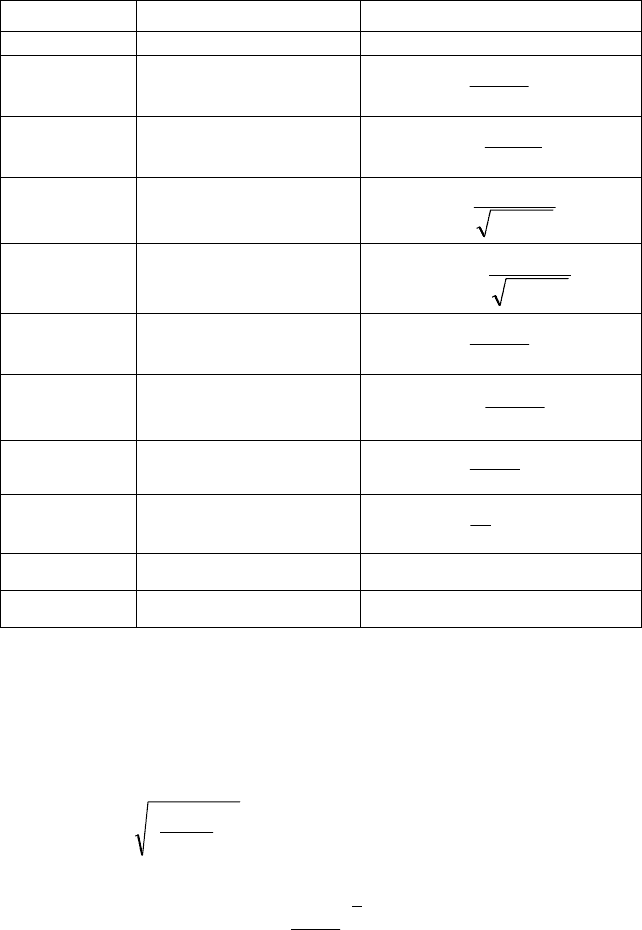
VIII
usiny = 'uucos'y ⋅=
IX
u
cos
y
=
'
u
u
sin
'
y
⋅−=
X
tgu
y
=
ucos
'u
'y
2
=
XI
ctgu
y
=
usin
'u
'y
2
−=
XII
uarcsiny =
2
u1
'u
'y
−
=
XIII
u
arccos
y
=
2
u1
'u
'y
−
−=
XIV
arctgu
y
=
2
u1
'u
'y
+
=
XV
arcctgu
y
=
2
u1
'u
'y
+
−=
XVI
ulogy
a
=
alnu
'u
'y =
XVIa)
ulny =
u
'u
'y =
XVII
u
ay = 'ualna'y
u
⋅=
XVIIa)
u
ey = 'ue'y
u
=
9.1. Приклади на використання таблиці похідних
Знайти похідні деяких функцій:
а)
42
)1x3x(y +−=
.
Розв
’язування. Використавши формулу (УІІ), одержимо
).3x2()1x3x(4)1x3x()1x3x(4y
32232
−+−=
′
+−+−=
′
б)
3
2
1x
1x
y
⎟
⎠
⎞
⎜
⎝
⎛
+
−
=
.
Розв
’язування. Перетворимо даний вираз, використавши дро-
бові показники степеня
3
2
1x
1x
y
⎟
⎠
⎞
⎜
⎝
⎛
+
−
=
. Використавши формули (VІІ)
і (VІ), одержимо

234
.
1x
1x
)1x(3
4
)1x(
2
1x
1x
3
2
)1x(
1x1x
1x
1x
3
2
)1x(
)1x()1x()1x()1x(
1x
1x
3
2
1x
1x
1x
1x
3
2
y
3
22
3
2
3
2
3
3
1
−
+
+
=
+
⋅
−
+
=
=
+
+−+
⋅
−
+
=
+
−
′
+−+
′
−
×
×
−
+
=
′
⎟
⎠
⎞
⎜
⎝
⎛
+
−
⎟
⎠
⎞
⎜
⎝
⎛
+
−
=
′
−
в)
x3
3)1x2x(y ⋅+−= .
Розв
’язування. Використавши формули (V) і (XVІІ), маємо
).3ln)1x2x(2x3(33ln3)1x2x(
3)2x3()3()1x2x(3)1x2x(y
32xx3
x2x3x3
+−+−=⋅+−
+⋅−=
′
⋅+−+⋅
′
+−=
′
г)
).1xx(lny
23
++=
Розв
’язування. Використавши формули (VIІ) і (XVIa), одер-
жимо
×
++
++
=
′
++⋅++=
′
1xx
)1xx(ln3
)1xx(ln()1xx(ln3y
2
22
222
=+⋅
++
++
=
′
++× )1x2(
1xx
)1xx(ln3
)1xx(
2
22
2
.
1
x
x
)1xx(ln)1x2(3
2
22
++
+++
=
д)
.x1xarcsinxy
2
−+=
Розв
’язування. Використавши формули (IV,V,VII б ,XII),
одержимо
=
′
−
−
+
′
+
′
=
′
)x1(
x12
1
)x(arcsinxxarcsin)x(y
2
2
.xarcsin
x
1
x
x
1
x
xarcsin)x2(
x12
1
x1
x
xarcsin
22
22
=
−
−
−
+
+=−
−
+
−
+=
е)
arctgx2
e)x1(y += (Розв’язати самостійно).
Відповідь:
arctgx
e)1x2(y +=
′
.

235
§10. Похідні вищих порядків
Похідна функції
у=f(x) є також функцією: у′=f′(x).
Ця функція також може мати похідну. Ця нова похідна нази-
вається другою похідною функції
у=f(x) або похідною функції f(x)
другого порядку і позначаться )x(''f''y = або
2
2
dx
yd
.
Похідна другої похідної, тобто функції
)x(''f''y =
назива-
ється третьою похідною або похідною третього порядку і познача-
ється символом
)x('''f'''y =
або
3
3
dx
yd
. Так можна ввести похідні
четвертого, п’ятого і взагалі
n – го порядку, які позначають
)n(VIV
y,...,y,y
.
Приклад 1. Знайти похідну четвертого порядку функції
1x2x5xy
34
−+−= .
Розв
’язування. Маємо ;2x15x4'y
23
+−=
;x30x12''y
2
−=
;30x24'''y −=
.24y
IV
=
Приклад 2. Знайти похідні
n-го порядку від функцій:
а)
x
ey = , б) xsiny = , в)
x
cos
y
= .
Розв
’язування.
а)
x
ey =
′
,
x
ey =
′′
,…,
x)n(
ey = ;
б)
);
2
xsin(xcosy
π
+==
′
);
2
2xsin(xsiny
π
⋅+=−=
′′
)
2
4xsin(xsiny
);
2
3xsin(xcosy
IV
π
⋅+==
π
⋅+=−=
′′′
і по індукції
).n
2
xsin(y
)n(
π
+=
236
в) аналогічно знаходимо )n
2
xcos(xcosy
)n()n(
π
+==
.
§11. Диференціал функції
11.1 Означення диференціала
Якщо функція
)x(fy = має в точці х похідну , то
x
y
lim)x('f
0x
Δ
Δ
=
→Δ
і приріст функції yΔ можна подати у вигляді
xx)x('fy Δα+Δ=Δ
, (4.3)
де
α
- нескінченно мала величина, яка прямує до нуля разом з
xΔ
.
В формулі (4.3) другий доданок
xΔα є нескінченно мала ви-
щого порядку, ніж
xΔ
і тому головну частину суми складає перший
доданок
x)x('f Δ
, який має назву диференціала функції.
Означення. Головна лінійна частина приросту функції, яка
дорівнює добутку похідної на приріст незалежної змінної назива-
ється диференціалом функції )x(f .
Позначається диференціал символом
dy
або
)x(df
. Отже,
x)x('fdy Δ= (4.4)
Приріст
xΔ
незалежної змінної також позначають так :
dxx =Δ .
Це пояснюють тим, що для функції
x
y
=
диференціал
xx'xdy Δ=Δ= . Тому рівність (4.4) записують dx)x('fdy = .
Приклад1
. Знайти диференціал функції
xln1y +=
.
Розв
’язування. dx
x
1
dx)'xln1(dy =+=
.
Приклад 2. Знайти диференціал функції
y=sin
3
2x.
Розв
’язування. Обчислимо спочатку похідну y′,
використавши правило диференціювання складної функції
.x2cosx2sin6)x2(x2cosx2sin3)x2(sinx2sin3y
222
=
′
=
′
=
′
Отже,
.xdx2cosx2sin6dy
2
=
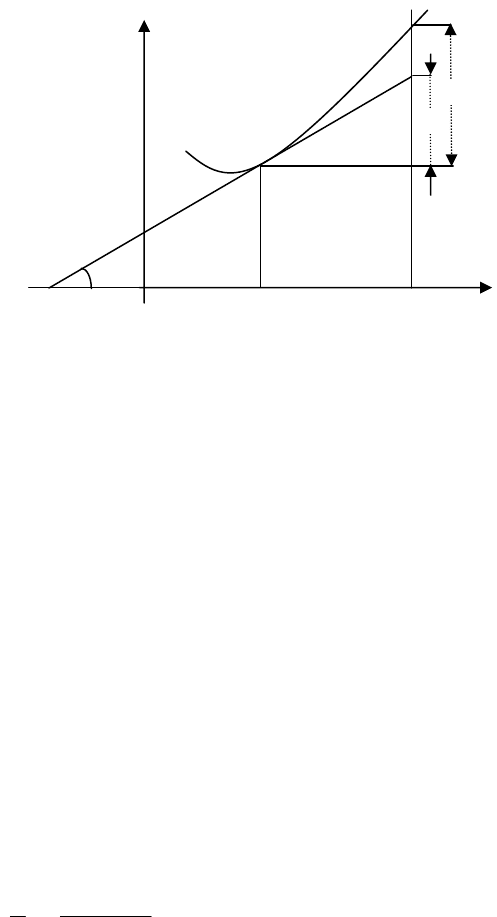
11.2. Геометричний зміст диференціала
Диференціал функції має просте геометричне тлумачення.
Нехай маємо графік функції
y=f(x). Візьмемо на цій кривій
237
точку М(х,у) і проведемо в ній дотичну до кривої.
Нехай
α - кут нахилу дотичної з додатнім напрямом осі ОХ.
Тоді
)x('ftg =α .
Надамо
х деякого приросту xΔ . На мал. 4 MCABx ==Δ .
Тоді ордината точки
М дістане приріст
1
CMy =Δ , а ордината точки
М, дотичної - приріст СД. Враховуючи, що
∠
ДМС=
α
, маємо
СД=МС
α
tg
або СД= dyx)x('f =Δ .
З геометричної точки зору диференціал
dy
функції
)x(fy = в даній точці є приріст ординати дотичної до графіка фун-
кції в цій точці, коли
x
дістає приріст .xΔ
11.3. Основні властивості диференціала
1). Диференціал сталої дорівнює нулю:
.0dc =
2).Диференціал алгебраїчної суми функцій дорівнює алгебраї-
чній сумі диференціалів цих функцій:
dvdu)vu(d ±=±
3) Диференціал добутку двох функцій дорівнює сумі добутків
кожної з функцій на диференціал другої функції:
.vduudv)vu(d +=⋅
4) Диференціал частки знаходиться за формулою
2
v
udvvdu
v
u
d
−
=
⎟
⎠
⎞
⎜
⎝
⎛
.
О
A
y
М
α
х
х+
Δх
В
C
D
М
1
Мал. 4
dy
Δ
y
x
238
Доведемо властивість 3):
.udvvdu
dxvudxuvdx)uvvu(dx)uv()vu(d
+=
=
′
+
′
=
′
+
′
=
′
=⋅
11.4. Властивість інваріантності форми диференціала
Нехай дана складна функція
)u(fy =
, де
)x(u
ϕ
=
.Тоді
'u)u('f'y
xx
= а du)u('fdx'u)u('fdx'ydy
xx
=== .
Оскільки
[]
dx)x('f)x(fddy ==
, то можемо зробити ви-
сновок, якщо замість незалежної змінної
х підставити довільну фун-
кцію від
х, то форма диференціала не змінюється. Ця властивість
носить назву інваріантності форми диференціала.
11.5. Застосування диференціалів при наближених
обчисленнях
Диференціали використовують при наближених обчисленнях
значень функцій, застосовуючи приблизну рівність
dyy ≈Δ . В роз-
горнутому вигляді маємо
x)x('f)x(f)xx(f
000
Δ≈−Δ+ .
Звідки значення функції
x)x('f)x(f)xx(f
000
Δ+≈Δ+
.
Приклад 1. Обчислити наближено
1ln ,02 з допомогою дифе-
ренціалу.
Розв
’язування. Число ln1,02 є значення функції xlny = при
х=1,02. Взявши 1x
0
= , =Δx 0,02, маємо 01ln)x(f
0
== ;
;
x
1
)x('f =
1
1
1
)x('f
0
== .
Отже,
ln 1,02= ln1+1
02,002,0 =⋅
.
Приклад 2. Обчислити
3
65
.
Розв
’язування. Запишемо
3
65
у вигляді
3
3
3
64
1
14)164(65 +=+=
. Будемо розглядати дане число як зна-
чення функції
3
x4y =
при
.
64
1
1x +=
Взявши
64
1
x,1x
0
=Δ=
і врахувавши, що
239
,
x3
4
x
3
4
x4y
3
2
3
2
3
1
==
′
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
=
′
−
маємо
414)1(f)x(f
3
0
=== ,
3
4
13
4
)1(f)x(f
2
0
==
′
=
′
,
і тому
.0208,4
48
1
4
64
1
3
4
465
3
≈=⋅+=
§12.Основні теореми диференціального числення
Похідна функції є важливим інструментом при
дослідженні властивостей функції. Перш ніж займатись
дослідженням властивостей функції, доведемо деякі важливі теоре-
ми.
12.1. Теорема Ферма
Незважаючи на те, що в час, коли жив відомий французький
математик П’єр Ферма (1601-1665), поняття похідної не було відо-
ме, суть того методу, який він застосовував при знаходженні
найбі-
льших і найменших значень функції виражає теорема, яку справед-
ливо називають теоремою Ферма.
ТЕОРЕМА ФЕРМА. Нехай функція
)x(fy = визначена в
інтервалі
)b,a(
і в деякій внутрішній точці
0
x
цього інтервалу
приймає найбільше чи найменше значення. Тоді, якщо в цій то-
чці існує похідна, то вона дорівнює нулю, тобто
0)x(f
0
=
′
.
Доведення
. Нехай в точці
0
x
функція
)x(f
приймає найбі-
льше значення, тобто
)x(f)x(f
0
≤ для будь-якого ).b,a(x∈ Це
значить, що
0)x(f)xx(fy
00
≤−Δ+=Δ для будь-якої точки
).b,a(xx
0
∈Δ+
Тому при 0x >Δ буде
0
x
y
≤
Δ
Δ
і
,0)x(f
x
y
lim
0
0x
≤
′
=
Δ
Δ
→Δ
а при
0x <Δ
маємо
0
x
y
≥
Δ
Δ
і
.0)x(f
x
y
lim
0
0x
≥
′
=
Δ
Δ
→Δ
Співставивши обидва співвідношення, одержуємо, що
f
′(x
0
)=0.

240
Аналогічно доводиться, що
0)x(f
0
=
′
у випадку, коли функ-
ція
)x(f в точці
0
x набуває
найменшого значення.
Перетворення в нуль
похідної функції
)x(f
0
′
гео-
метрично означає, що в цій
точці
0
x дотична до графіка
функції
)x(fy =
паралельна
осі
x0 (мал. 5).
12.2.Теорема Ролля
ТЕОРЕМА. Якщо
)x(f
функція неперервна на замкну-
тому проміжку
[]
b,а
і має похідну в кожній внутрішній точці
цього проміжку, а на кінцях його приймає однакові значення
),b(f)a(f = то тоді принаймні в одній внутрішній точці промі-
жку її похідна дорівнює нулю.
Доведення. Розглянемо дві можливості.
1.Функція
)x(f зберігає стале значення на всьому проміжку
[]
b,а
, тобто
.C)x(f =
Тоді
0)x('f =
для всіх х є
[]
b,а
і теорема
доведена.
2.Функція
)x(f
не є сталою. Як неперервна функція на за-
мкненому проміжку, вона досягає свого найбільшого
М і свого най-
меншого
m значення за теоремою Вейєрштраса. Принаймні одне з
цих значень функція приймає всередині проміжку, бо тільки одне з
них може прийматись на кінці проміжку. Припустимо для визначе-
ності, що функція приймає все-
редині найбільше значення
М в
точці
0
xx = , тобто .M)x(f
0
=
Через те, що
0
x є внутрі-
шньою точкою проміжка
)b,a( і
функція
)x(f за умовою має
похідну в ній, то за теоремою
Ферма похідна
.0)x(f
0
=
′
Доведення аналогічне для
b
х
0
а
O
у
х
Мал.5
x
B
O
f(b)
f(a)
a
b
A
x
0
y
Мал.6
