Шинкарик М.І. Вища математика
Подождите немного. Документ загружается.


211
шим) значенням функції
)x(f
на множині
D
, якщо для будь-якого
Dx∈ правильна нерівність )x(f)x(f ≤
∗
)).x(f)x(f( ≥
∗
Най-
менше і найбільше значення функції не завжди існують.
Однак правильна теорема.
ТЕОРЕМА 2 (Вейєршрасса). Якщо функція
)x(f
непере-
рвна на відрізку
[]
b,a , то серед її значень на цьому відрізку існує
найменше і найбільше, тобто
[]
)x(f)x(fmin
1
b,a
=
,
[]
b,ax
1
∈
і
)x(f)x(f
1
≥
,
[]
b,ax∈
;
[]
)x(f)x(fmax
2
b,a
=
,
[]
b,ax
2
∈
і
)x(f)x(f
2
≤ ,
[]
b,ax∈ .
Доведення
. Оскільки функція
)x(f
неперервна на відрізку
[]
b,a , то за теоремою 1 всі її значення обмеженні, тобто
M)x(fm ≤≤ , де
m
і
M
- сталі величини. Тоді для такої множини
{}
)x(f значень функції існує точна верхня межа. Нехай
{}
.)x(fsup=
μ
Припустимо, що
)x(f≠
μ
, коли
[]
b,ax∈
.
Розглянемо нову функцію
)x(f
1
)x(
−μ
=ϕ
.
Оскільки
,0)x(f ≠−
μ
[]
b,ax∈ , то функція )x(
ϕ
неперервна на відрізку
[]
b,a
, а значить за теоремою 1 вона обмеже-
на, тобто існують числа
α і
β
такі, що
β
≤
ϕ
≤α )x(
(
)0>
β
.
Розглянемо нерівність
β≤
−μ )x(f
1
.
Звідси одержуємо, що
,
1
)x(f
β
≥−μ ,
1
)x(f
β
+μ−≥− .
1
)x(f
β
−μ≤
Остання нерівність показує, що число
μ
не може бути точною
верхньою межею. Отже, наше припущення неправильне. Теорема 2
доведена.
6.3. Теорема про перетворення функції в нуль
Для доведення наступної властивості функцій, неперервних на
відрізку, потрібна одна локальна властивість неперервної функції.
212
ДОПОМІЖНА ТЕОРЕМА. Якщо функція
)x(f
непере-
рвна в точці
x
0
справа (зліва) і якщо 0)x(f
0
≠ , то знайдеться
число
δ>0 таке, що для всіх
[
)
δ+∈
00
x,xx
(
(
]
000
x,xx δ−∈
) зна-
чення функції
)x(f
за знаком будуть такими, як
)x(f
0
.
Доведення
. Нехай для означеності f(x
0
)>0 і функція )x(f не-
перервна в точці
0
x справа. Тоді для числа 0
2
)x(f
0
>=ε
існує число
0>δ
таке, що для всіх
[
)
δ+∈
00
x,xx буде правильна
нерівність
2
)x(f
)x(f)x(f
0
0
=ε<− .
Звідси для
[
)
δ+∈
00
x,xx маємо
.0
2
)x(f
)x(f)x(f
0
0
>=ε−>
Теорема доведена для розглядуваного випадку. Інші випадки
доводяться аналогічно.
Наслідок
1. Якщо функція
)x(f
неперервна в точці
0
x
і як-
що
0)x(f
0
≠
, то знайдеться окіл
)x,x(
00
δ+δ−
точки
0
x
, для
всіх точок
x
якого значення функції )x(f за знаком будуть таки-
ми ж, як
)x(f
0
.
ТЕОРЕМА 3 (Больцано-Коші). Якщо функція
)x(f непере-
рвна на відрізку
[]
b,a
і якщо значення цієї функції на кінцях цьо-
го відрізка протилежні за знаком, то існує принаймні одна точка
с
∈(а,b), значення функції в якій дорівнює нулю, тобто
0)c(f =
.
Доведення
. Нехай для означеності
0)а(f <
,
0)b(f >
. Оскіль-
ки функція
)x(f в точці
a
x
=
неперервна справа , а в точці x=b не-
перервна зліва, то за допоміжною теоремою знайдеться число
0>δ
таке, що
0)x(f <
для всіх
[
)
δ+∈ a,ax
і
0)x(f >
для всіх
x∈(b-δ,b). Позначимо через
D
множину всіх точок x∈[a,b] в яких
f(x)<0. Ця множина непорожня, оскільки
[
)
Da,a ⊂δ+ . Вона обме-
жена зверху числом
δ−b . Така множина має точну верхню межу.
Позначимо її через
Dsupс = . Ясно, що
δ−≤≤δ+ bca
і, отже,
)b,a(с ∈ . Доведемо рівність 0)с(f = .
213
Припустимо, що
0)с(f ≠
. Оскільки
)b,a(с ∈
, то за наслід-
ком 1 допоміжної теореми знайдеться окіл
21
с,с( δ+δ− ) точки
с
, в
усіх точках якого значення функції
)x(f
за знаком будуть такими ж,
як
)с(f .
Якщо
0)с(f < , то 0)x(f < для всіх
21
с,с(x δ+δ−∈ ), що
суперечить означенню числа
с як верхньої грані множини
D
всіх
тих точок
[]
b,ax∈ , в яких 0)x(f < .
Якщо
0)с(f >
, тоді
0)x(f >
для всіх
21
с,с(x δ+δ−∈
), що
знову ж таки суперечить означенню числа
с
як верхньої грані мно-
жини
D
, бо за властивістю верхньої грані в проміжку
)с,с(
1
δ−
міститься проміжна одна точка
x
′
з множини
D
, в якій
0)x(f <
′
.Припущення, що 0)с(f ≠ , привело до суперечності.
Отже,
0)с(f = і теорему 3 доведено.
§7. Деякі економічні задачі і їх розв’язування
Задача 1. Бюро економічного аналізу підприємства встанови-
ло, що при виробництві
x
комплектів меблів щоквартальні витрати
)x(V
виражаються формулою
x152050)x(V +=
(гривень), а дохід
)x(D , одержаний від продажу
x
комплектів меблів визначається
формулою
2
x1,0x25)x(D −=
(гривень) .
Кожного кварталу підприємство виробляє 80 комплектів, але
прагне збільшити випуск меблів до 110 одиниць. Обчислити приріст
витрат, доходу та прибутку. Знайти середню величину приросту
прибутку на одиницю приросту продукції :
Розв
’язування. Запланований приріст продукції буде
3080110x =−=Δ
(одиниць продукції).
Приріст витрат :
.45032503700
)
80
15
2050
(
)
110
15
2050
(
)
80
(
V
)
110
(
V
)
x
(
V
=−=
=⋅+−⋅+=−=Δ
Приріст доходу:
.18013601540
)801,08025()1101,011025()80(D)110(D)x(D
22
=−=
=⋅−⋅−⋅−⋅=−=Δ
Позначимо прибуток через
).x(Р
Тоді прибуток буде:
214
.x1,0x102050
x152050x1,0x25)x(V)x(D)x(P
2
2
−+−=
=−−−=−=
Приріст прибутку буде таким:
27064080012101100)801,080102050(
1101,0110102050)80(P)110(P)x(P
2
2
−=+−−=⋅−⋅+−−
−⋅−⋅+−=−=Δ
тобто зменшиться на 270 гривень. Середня величина прибутку на
одиницю приросту продукції буде
.67,1
30
50
)x(
)x(P
−=
−
=
Δ
Δ
Задача 2. В одному із обласних центрів в усіх вищих навчаль-
них закладах навчається 35 тис. студентів. Щорічно кількість студе-
нтів збільшується на 3%. Яка кількість студентів буде у вказаному
обласному центрі через вісім років?
Розв
’язування. Використаємо формулу зростання за складни-
ми відсотками:
,)i1(К)
100
р
1(КК
t
0
t
0t
+=+=
де
t
K
– сума вкладу, нагромаджена через
t
років;
−
0
К
початкова
сума вкладу;
−р
щорічний відсотковий приріст;
t
– період зрос-
тання в роках;
,
100
р
i = ri1 =+ - коефіцієнт складних відсотків.
На основі формули зростання за складними відсотками маємо:
34,44)03,01(35)
100
3
1(35
К
88
8
≈+⋅=+= (тис. студентів).
Задача 3. Вкладник надає банку 2000 гривень під складні від-
сотки з умовою їх неперервного зростання на 12% річних. Обчисли-
ти нагромадження капіталу за 4 роки.
Розв
’язування. Використаємо формулу неперервного зростан-
ня за складними відсотками
.eKeKK
it
0
t
100
p
0t
=⋅=
Якщо
0p > , формула називається показниковим законом зро-
стання, а при
0p <
- показниковим законом спадання.
На основі формули неперервного зростання за складними від-
сотками одержуємо таку відповідь:
.грн.тис2322,3е2000К
12,04
4
=⋅=
⋅

215
Розділ 4. ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ ФУНКЦІЙ
ОДНІЄЇ ЗМІННОЇ
Закономірності, які вивчають різні галузі науки, в тому числі
й економіки, описуються за допомогою функцій. Описавши процес
функцією, дослідження процесу зводиться до вивчення властивос-
тей функції. Відповідь на такі питання , як швидкість процесу в да-
ний момент, проміжки часу, коли буде прискорення чи уповільнен-
ня процесу та інші можна одержати за допомогою похідної даної
функції.
§1. Означення похідної
Уточнимо поняття похідної функції, з яким знайомі з шкіль-
ного курсу математики.
Нехай задано функцію
),x(fy =
визначену на проміжку
).b,a( Візьмемо деяку точку
0
x з цього проміжку. Значення функції
в ній буде
).x(fy
00
= Hадамо аргументу приріст Δ х, такий, що
точка
xxx
01
Δ+= не вийде за вказаний проміжок.Тоді функція
одержить нове значення
yy)xx(f
00
Δ+=Δ+
, а її приріст
)x(f)xx(fy
00
−Δ+=Δ . Складемо відношення
приросту функції до приросту аргументу
x
)x(f)xx(f
x
y
00
Δ
−Δ+
=
Δ
Δ
. (4.1)
Знайдемо границю відношення (4.1) при умові, що
xΔ прямує
до нуля. Якщо ця границя існує, то її називають похідною функції
)x(fy =
в точці
0
x
і позначають
)x(f
0
′
.
x
)x(f)xx(f
lim
x
y
lim)x(f
00
0x0x
0
Δ
−Δ+
=
Δ
Δ
=
′
→Δ→Δ
.
Якщо похідна існує для всіх точок проміжку,то вона є функці-
єю від х . Для кожного конкретного значення
0
xx =
похідна є чис-
ло.
Означення. Похідною функції у = f(x) в точці х називається
границя відношення приросту функції в цій точці до приросту
аргументу, коли приріст аргументy прямує до нуля.
216
Похідну позначають так: .
dx
df
,
dx
dy
,f,y,y
x
′′′
x
)x(f)xx(f
lim
x
y
limy
00
0x0x
Δ
−Δ+
=
Δ
Δ
=
′
→Δ→Δ
.
Покажемо застосування цього означення для знаходження по-
хідних деяких функцій.
Приклад 1
. Знайти похідну функції
2
xy = .
Розв
’язування.
1. Надаємо аргументу х приросту Δ х.
2. Знаходимо приріст функції
yΔ
, віднявши від значення фу-
нкції в новій точці значення функції в початковій точці
=−Δ+Δ+=−Δ+=Δ
22222
x)x(xx2xx)xx(y
.)x(xx2
2
Δ+Δ=
3. Складаємо відношення приростів
.xx2
x
)x(xx2
x
y
2
Δ+=
Δ
Δ+Δ
=
Δ
Δ
4. Обчислюємо границю цього відношення при умові , що
приріст аргументу
xΔ прямує до нуля
х2)хх2(lim
x
y
limy
0x0x
=Δ+=
Δ
Δ
=
′
→Δ→Δ
.
Отже,
x2y =
′
або
x2)x(
2
=
′
.
Приклад 2. (самостійно). Знайти похідну функції
x
y
=
. Від-
повідь:
.1y =
′
Приклад
3. Знайти похідну функції у=sin x.
Розв’язування.
1. Надаємо довільному х приросту xΔ .
2. Знаходимо приріст функції
=
+Δ+
⋅
−Δ+
=−Δ+=Δ
2
xxx
cos
2
xxx
sin2xsin)xxsin(y
cos
2
x
sin2
Δ
=
(x+ ).
2
xΔ
3. Складаємо відношення приростів
.
x
1
)
2
x
xcos(
2
x
sin2
x
y
Δ
⋅
Δ
+
Δ
=
Δ
Δ
217
4. Обчислюємо границю цього відношення при умові , що
.0x →Δ
=
Δ
Δ
=
′
→Δ
x
y
limy
0x
=
Δ
+
Δ
Δ
→Δ
)
2
x
xcos(
2
x
2
x
sin
lim
0x
xcosxcos1)
2
x
xcos(lim
2
x
2
x
sin
lim
0x0x
=⋅=
Δ
+
Δ
Δ
=
→Δ→Δ
.
Отже,
(sin x)
′
= cos x.
Таким способом можна довести, що xsin)сosx( −=
′
.
§2. Задачі, що приводять до поняття похідної
2.1.Геометричний зміст похідної
Однією з задач геометрії, яка тісно пов’язана з історією вини-
кнення диференціального числення є задача про проведення дотич-
них до кривих.
Означення. До-
тичною до кривої, за-
даної рівнянням
)x(fy = в точці до-
тику
)y,x(M
назива-
ють граничне поло-
ження
MT
січної
MP
,
коли точка
P
, рухаю-
чись по кривій прямує
до точки
M
.
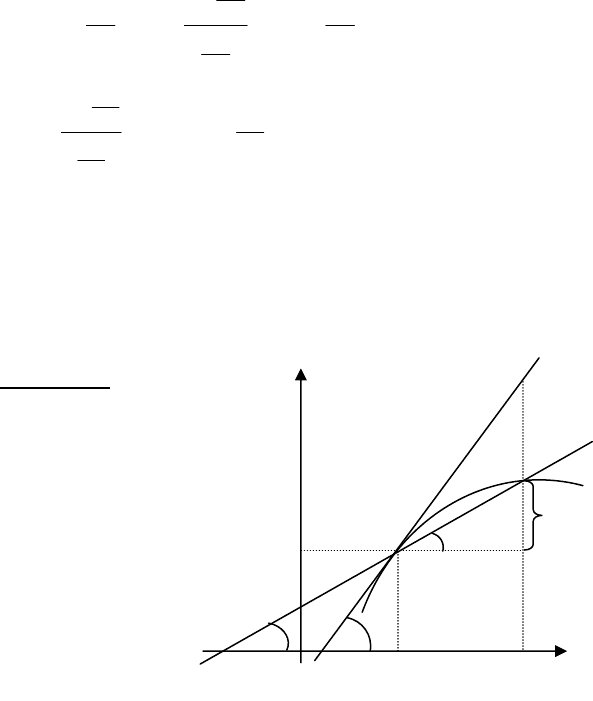
Розглянемо
графік y=f(x).
Візьмемо на графіку
точку М(x,y) і другу
точку
Р(
).yy,xx Δ+Δ+
Про-
ведемо січну МР і позначимо кут нахилу її до додатнього на-
прямку осі Ox через
ϕ
. Позначимо кут, який утворює дотична
MT
з додатнім напрямом осі x0 через
α
.
Якщо пересувати точку Р по кривій до точки М, то гра-
ничним положенням січної МР буде дотична МТ до графіка в
точці М. Як
видно з
малюнка
),x(fAM = =
BP
f(
xx Δ+
),
у
у
О
М
Q
Р
Т
В
А
Δ
y
х
α
φ
φ
х+
Δх
х
Δ
х
Мал
.
1

218
xABMQ;y)x(f)xx(fBQBPQP Δ==Δ=−Δ+=−= .
Отже,
x
y
x
)x(f)xx(f
MQ
QP
tg
Δ
Δ
=
Δ
−Δ+
==ϕ
,
а
α=
′
=
Δ
Δ
=ϕ
→Δ→Δ
tg)x(f
x
y
limtglim
0x0x
.
Отже, похідна в даній точці
x дорівнює тангенсові кута, утво-
реного дотичною до графіка функції в точці
)y,x(M з додатнім
напрямом осі
Ox
. Інакше, похідна в точці x дорівнює кутовому ко-
ефіцієнту дотичної до графіка функції в точці
)).x(f,x(
2.2. Дотична і нормаль до графіка функції
Задача. Знайти рівняння дотичної і нормалі до кривої, заданої
рівнянням
)x(fy = в точці з абсцисою
0
x .
Розв
’язування.Точка
M
на кривій має координати
0
xx =
)x(fyy
00
==
. Кутовий коефіцієнт дотичної
).x(fk
0
′
=
Викори-
ставши рівняння прямої з кутовим коефіцієнтом на площині, що
проходить через задану точку
M
, одержимо рівняння дотичної:
).xx)(x(fyy
000
−
′
=−
Нормаль до кривої в заданій точці перпендикулярна до
дотичної, проведеної в цій точці. А тому кутовий коефіцієнт
нормалі на основі умови перпендикулярності двох прямих
)x(f
1
k
1
k
0д
н
′
−=−=
. Отже, рівняння нормалі
).xx(
)x(f
1
yy
0
0
0
−
′
−=−
Приклад. Знайти рівняння дотичної і нормалі до параболи
2
xy =
в точці з абсцисою 2x = .
Розв
’язування. Похідна ,x2y =
′
.422)2(y =⋅=
′
Знайдемо
ординату цієї точки
.42)2(y
2
==
Рівняння дотичної
)2x(44y −=−
або
4x4y −=
.
Рівняння нормалі
)2x(
4
1
4y −−=−
або
2
9
4
x
y +−=
.

219
2.3. Механічний зміст похідної
Нехай матеріальна точка рухається по прямій, починаючи з
точки
O і шлях, пройдений нею, описується рівнянням )t(fs =
Зафіксуємо момент часу
t
,коли точка знаходилася в поло-
женні
M
.Надамо часу
t
приріст .tΔ За цей час точка перейде в по-
ложення
1
M . Приріст шляху
1
MMs =Δ (мал.2).
OMs =Δ
1
-
).t(f)tt(fOM −Δ+=
Середня швидкість руху
V
сер.
.
t
s
Δ
Δ
=
Спрямувавши
tΔ
до нуля, ми одержимо миттєву
швидкість руху точки
M
в момент часу
t
.
).t(f
t
)t(f)tt(f
lim
t
s
lim
0t0t
′
=
Δ
−Δ+
=
Δ
Δ
=
→Δ→Δ
V
Отже, похідна від пройденого шляху
s
по часу
t
виражає
миттєву швидкість руху в момент
t. Це є механічний зміст похідної.
2.4. Економічний зміст похідної
Якщо слово “швидкість” розуміти більш широко , як швид-
кість зміни функції в залежності від зміни аргументу, то можна вка-
зати економічний зміст похідних від функцій, які описують певні
економічні процеси.
Нехай витрати виробництва
V однорідної продукції є функці-
єю кількості продукції
x
, тобто ).x(VV = Припустимо, що кіль-
кість продукції збільшується на
xΔ . Продукції xx Δ+
відповідають витрати виробництва
)xx(V Δ+ . Приріст
витрат виробництва
)x(V)xx(VV −Δ+=Δ . Середній приріст ви-
трат на одиницю приросту продукції
x
V
Δ
Δ
.
Похідна
x
V
lim)x(V
0x
Δ
Δ
=
′
→Δ
називається маржинальними
(або граничними) витратами виробництва при умовах хоча би
простого відтворення виробництва продукції.
Вкажемо на економічний зміст похідних для інших залежнос
тей, які найбільш часто вживаються.
O
M
M
1
Мал.
220
Позначимо через
)x(D
та
)x(P
відповідно дохід і прибуток
при виробництві і реалізації
x
одиниць продукції. Тоді, якщо підп-
риємство збільшує випуск продукції на
xΔ одиниць, ці
функції одержать приріст
)x(D)xx(D)x(D −Δ+=Δ ,
)x(P)xx(P)x(P −Δ+=Δ
,
а тому маржинальний дохід
x
)x(D)xx(D
lim
x
)x(D
lim)x(D
0x0x
Δ
−Δ+
=
Δ
Δ
=
′
→Δ→Δ
,
а маржинальний прибуток
x
)x(P)xx(P
lim
x
)x(P
lim)x(P
0x0x
Δ
−Δ+
=
Δ
Δ
=
′
→Δ→Δ
.
§3. Зв’язок між неперервністю та диференційовністю фукції
Означення. Функції, які мають похідні в точці
x
назива-
ють диференційованими в цій точці.
Зв’язок між неперервністю і диференційовністю функції вста-
новлює наступна теорема.
ТЕОРЕМА. Якщо функція
)x(fy = диференційовна
в точці
,x
0
то вона неперервна в цій точці.
Доведення. Оскільки функція
)x(fy = диференційовна в то-
чці
,x
0
то вона має в цій точці скінчену похідну. Це означає, що
)x(f
x
y
lim
0
0x
′
=
Δ
Δ
→Δ
.
На основі означення границі випливає, що
,)x(f
x
y
0
α+
′
=
Δ
Δ
де
α - нескінченно мала величина.
Звідси
xx)x(fy
0
Δα+Δ
′
=Δ . А тому ,0y →Δ коли 0x →Δ .
А з означення неперервності функції випливає , що
)x(fy =
неперервна в точці
0
x
. Теорема доведена.
Обернене твердження неправильне.
Так, функція
xy =
неперервна в точці
0x =
(мал.3), але
вона немає похідної в цій точці. Дійсно,
