Шинкарик М.І. Вища математика
Подождите немного. Документ загружается.


181
x
1
,x
2
,… і навпаки, якщо задано послідовність її першими членами,
то можна завжди записати її загальний член. Наприклад, нехай
1)
n
1
x
n
=
, n ∈N .
Маємо
,1x
1
=
2
1
x
2
= ,
3
1
x
3
= ,……..,
n
1
x
n
= ,…
2)
2
1
x
1
= ,
3
2
x
2
= ,
4
3
x
3
= ,….
Звідси випливає, що
1n
n
x
n
+
=
, n ∈N .
Як вже зазначалося вище, для задання послідовності необхідно
знати правило, за яким кожному значенню n ставиться у відповідність
дійсне число x
n
=f(n). Таке правило може бути задане за допомогою фо-
рмули, як це зроблено у наведених вище прикладах. Проте є інші спо-
соби задання послідовностей. Наприклад, візьмемо за (x
n
)
n
-ну цифру
розкладу числа π у нескінчений десятковий дріб. Матимемо послідов-
ність 3,1,4,1,…
Тут правило відповідності задано словесно.
Іноді при заданні послідовності задається її перший член і прави-
ло утворення n-го члена за допомогою попередніх членів. Такий спосіб
називається рекурентним. Наприклад, нехай перший член послідовнос-
ті дорівнює 2, а кожний наступний дорівнює попередньому, помноже-
ному на 10. Тоді x
n+1
=10x
n
, x
1
=2,n ∈N .
Серед числових послідовностей в окремий клас виділяють так
звані монотонні послідовності, що об’єднують в собі зростаючі, спадні,
неспадні, незростаючі послідовності.
Означення 2. Послідовність (x
n
) називається зростаючою,
якщо кожний її наступний член більший від попереднього, тоб-
то
n1n
xx >
+
для кожного
n
.
Наприклад, послідовність, ,...n,...,3,2,1
222
є зростаюча.
Означення 3. Послідовність (x
n
) називається неспадною,
якщо
n1n
xx ≥
+
для кожного
n
.
Наприклад, послідовність ,...2,2,1,1,1 є неспадна.
Означення 4. Послідовність (x
n
) називається спадною,
якщо
n1n
xx <
+
для кожного
n
.
Наприклад, послідовність ,...
n
1
,...,
3
1
,
2
1
,1
є спадна.
182
Означення 5. Послідовність ( )x
n
називається незростаю-
чою, якщо
n1n
xx ≤
+
для кожного
n
.
Для дальшого вивчення числових послідовностей необхідно
ввести в розгляд такі арифметичні операції над числовими послідо-
вностями: додавання, віднімання, множення та ділення.
Нехай маємо дві послідовності
,...x,...,x,x
n21
,...y,...,y,y
n2`1
Тоді додавання, віднімання та множення двох послі-
довностей виконуються додаванням, відніманням та мно-
женням відповідних членів цих послідовностей.
Якщо всі ,0y
n
≠ n ∈N , то частка від ділення послідовності
( )x
n
на послідовність )y(
n
визначається як послідовність
,...z,...,z,z
n2`1
члени якої
n
n
n
y
x
z =
, n ∈N .
Символічно ці дії позначаються так:
()
;yx)y()x(
nnnn
±=±
()
;yx)y()x(
nnnn
⋅=⋅
).
y
x
(
)y(
)x(
n
n
n
n
=
Означення 6. Числова послідовність )x(
n
називається об-
меженою, якщо існують дійсні числа
m
і
M
такі, що для всіх
n
∈N виконуються нерівності Mxm
n
≤≤ .
У протилежному випадку послідовність називається
необмеженою.
Часто користуються еквівалентним означенням обмеженості
послідовності.
Означення 7. Числова послідовність )x(
n
називається
обмеженою, якщо існує дійсне число С таке, що для всіх
n
∈ N виконується нерівність |x
n
|≤C.
Частинними випадками послідовності є арифметична та гео-
метрична прогресія.
Означення 8. Арифметична прогресія - це числова послідо-
вність, кожен член якої, починаючи з другого , дорівнює поперед-
183
ньому, збільшеному на число d, яке називається різницею прогре-
сії.
daa
n1n
+=
+
,
Nn∈
.
Наприклад, для послідовності
12,+2,-8,-18,…, а
1
=12 і 10d −= .
Загальний член арифметичної прогресії знаходиться за фор-
мулою:
(
d)1іaa
1і
−+=
.
Сума
n
членів скінченої арифметичної прогресії
дорівнює:
n
2
aa
S
n1
n
+
=
або n
2
d)1n(
а2
S
1
n
⋅
−+
= .
Ці поняття і формули застосовуються при нарахуванні прос-
тих відсотків.
Так, якщо сума капіталу
P вкладена під R відсотків річних,то
після першого року буде одержано прибуток величиною
%100
R
Pd =
.
Якщо вкладення капіталу здійснюється під простий річний ві-
дсоток, то прибуток зростає на однакову величину з кожним роком:
P,
P+d, P+2d,…,. Ці значення утворюють арифметичну прогресію.
Отже, величина капіталу
P, що вкладений під простий річний відсо-
ток
R , через n років буде
)
%100
nR
1(P
%100
PR
nPndPa
n
+=+=+=
.
Наприклад, вкладається 50000 гр. під простий річний відсоток
25%. Тоді через два роки вкладник матиме
75000)
2
1
1(50000)
%100
%252
1(50000a
2
=+=
⋅
+=
.
Часто
i
100
R
=
- називають питомою відсотковою ставкою (або нор-
мою відсотка). Отже,
)ni1(PaP
nn
+==
.
Означення 9. Геометричною прогресією називається послі-
довність, кожний наступний член якої дорівнює попередньому,
помноженому на одне і те саме число
q
, яке називається зна-
менником геометричної прогресії.
Якщо 1q < - прогресія спадна, q >1 – прогресія зростаюча.
За означенням
qbb
n1n
=
+
або
1n
1n
qbb
−
= .

184
Сума n членів скінченої геометричної прогресії знаходиться
за формулою
q1
)q1(b
S
n
1
n
−
−
=
.
Сума членів нескінченої спадної геометричної прогресії зна-
ходиться за формулою:
q1
b
S
1
n
−
=
.
Припустимо, що вкладник дає банку 50000 грн. з умовою що-
річного зростання на 25% складних відсотків , тобто щороку вели-
чина капіталу, що знаходиться на рахунку вкладника в банку по-
винна зростати на 25%. Після 1-го року матимемо:
500006250050000
100
25
50000 ==⋅+ 62500)
4
1
1( =+
.
Після другого року:
78125)
4
1
1(50000)
4
1
1(6250062500
100
25
62500
2
=+=+=⋅+
.
Зрозуміло,що після
т
-го року матимемо
т
)
4
1
1(50000 +
, то-
му величина капіталу
P, що зростає щороку на R складних відсотків,
через
n
– років прийме значення:
n
n
)R01,01(PP += .
Найпростішим типовим рахунком накопичення є такий раху-
нок фізичної або юридичної особи, на який регулярно нараховується
відсоткова ставка і зараховується новий вклад.
Задача. Кожного місяця працівник (студент) вносить 100 гри-
вень на свій рахунок накопичення з одержанням прибутку величи-
ною 2% щомісячно. Обчислимо величину його накопичень:
а
) після здійснення 24 внеску;
б
) після здійснення n внеску.
Кожний внесок за місяць зростає в 1,02. Тому перший внесок
за 23 місяці перебування на рахунку прийме значення
100(1,02)
23
.
Другий внесок знаходився на рахунку 23 місяці
(100(1,02)
22
) і т.д.
Загальна сума накопиченого рахунку студента прийме зна-
чення:
()
.100...)02,1(10002,1100S
2223
+++= 02,1q;100b
1
== .
Отже,
=
−
=
−
−
=
−
−
=
02,0
)1)02,1((100
02,11
))02,1(1(100
q1
)q1(b
S
2424n
1
185
.1852,3042421852,30100)1)02,1((5000
24
=⋅=−
i
n
SPS ⋅= - формула накопичення.
◙ Розрахунки ренти
Багато людей в країнах з ринковою економікою живуть за ра-
хунок ренти, тобто регулярно на протязі певного терміну одержу-
ють обумовлену суму коштів з відповідного рахунку в банку або
страховій компанії. Скільки треба поставити на рахунок ренти, щоб
одержувати відповідні кошти?
Нехай
А – величина внеску на рентний рахунок. З цього раху-
нку здійснюються виплати
Р щорічно на протязі n років і величина
внеску щорічно зростає на
R відсотків.
1
A
- кошти, які вкладені на рахунок ренти і дадуть через один
рік виплату
Р.
Отже,
1
11
)i1(PA,
100
R
i,P)i1(A
−
+===+ .
2
A - кошти, які вкладені на рахунок ренти і через два роки да-
дуть виплату
Р.
2
22
)i1(PA;P)i1(A
−
+==+ і т.д.
n
n
)i1(PA
−
+= .
Таким чином на рахунок ренти треба покласти суму:
n21
n21
)i1(P...)i1(P)i1(PA...AA
−−−
++++++=+++
.
Це сума
n –членів геометричної прогресії:
1
1
)i1(Pb
−
+= і
1
)i1(q
−
+= .
;Pa
)i1(1
))i1(1()i1(P
SA
i
n
1
n1
=
+−
+−+
=≡
−
−−
де
).)i1(1(ia
n1
i
n
−−
+−=
◙ Погашення боргу
Процес повернення боргу регулярно, певними частинами, в
певний термін і протягом домовленого часу з виплатою певного від-
сотку називається погашенням боргу.
З математичної точки зору погашення боргу – це задача про
ренту.
Страхова компанія взяла в борг суму А
і виплачує
186
борг:
i
n
aPA ⋅=
;
i
n
a
A
P =
.
Задача. На час навчання студент академії народного госпо-
дарства отримав з фонду навчання в борг 17000 грн. Цей кредит йо-
му надано із 8% щорічного зростання і умовою повернення (щоріч-
но) в кінці кожного року після закінчення академії протягом 15 ро-
ків. Скільки коштів повинен повертати студент кожного року?
17000A = ,
,15n =
,8R =
,08,0
100
8
i ==
.грн1986
559479,8
1700
a
A
P
08,0
15
===
3.2. Границя числової послідовності
Розглянемо такі числові послідовності:
1)
,...,
n
1
,...,
3
1
,
2
1
,1
де
;
n
1
x
n
=
2)
,...,
1n
n
,...,
4
3
,
3
2
,
2
1
+
де ;
1n
n
x
n
+
=
3)
,...,
n
)1(
,...,
4
1
,
3
1
,
2
1
,1
1n−
−
−−
де ;
n
)1(
x
1n
n
−
−
=
4)
,...,)1(,...,1,1,1,1
1n−
−−− де
1n
n
)1(x
−
−= .
Аналізуючи наведені приклади, можна стверджувати, що
змінна
x
n
при зростанні n (
n
∞→ - “ен” прямує до нескінченості ) в
прикладі 1)наближається до нуля ( залишаючись більшою від нуля);
в прикладі 2) змінна зростає, наближаючись до одиниці (залишаю-
чись меншою за одиницю); в прикладі 3) відбувається процес на-
ближення змінної до нуля, але її значення коливається в околі нуля;
в прикладі 4) не можна визначити до якого числа наближається
змінна
1n
n
)1(x
−
−= ,
n
∈
N
. Оскільки в прикладах 1)–3) є те, що
змінна
n
x при зростанні
n
наближається до сталої величини, то в
таких випадках говорять, що змінна
n
x
має границю при n ∞→ .
Означення. Число а називається границею числової послі-
довності (
n
x ), якщо для будь-якого наперед заданого як завгодно
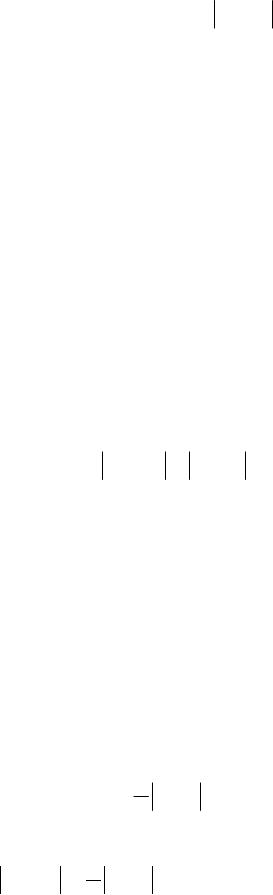
187
малого додатного числа 0>ε існує такий номер
N
, починаючи
з якого виконується нерівність
ε<− ax
n
, (3.5)
як тільки
n
≥
N
.
Той факт, що
a
є границею послідовності (
n
x
), символічно
записують так
:
axlim
n
n
=
∞→
або ax
n
→ (при
∞→
n
). (3.6)
Ми будемо користуватися першим позначенням (
lim - від ла-
тинського слова
eslim , що означає “границя”).
Отже, в розглянутих нами прикладах 1)–3) границі вказаних
послідовностей відповідно дорівнюють
1)
;0а = 2) ;1а = 3) ,0а = а для прикладу 4) відповідь така:
границя не існує.
Враховуючи нерівність (3.5), стверджуємо, якщо послідов-
ність (
n
x
) має границею число а , то , починаючи з деякого номера
N
всі її члени знаходяться в околі )a,a( ε+ε− точки
а
.
Примітка
. Якщо
n
x С= , сonstС = (С - стала величина), то
зрозуміло , що
ε<=−=− 0ССCx
n
для всіх ,...3,2,1n = Тому
справедливе таке твердження: Границя сталої величини дорівнює
цій сталій величині, тобто,
.CClim
n
=
∞→
Послідовність, яка має скінчену границю, називається
збіжною, у протилежному випадку - розбіжною.
3.3. Основні теореми про границі числових послідовностей
ТЕОРЕМА 1. Послідовність може мати тільки одну грани-
цю.
Доведення
. Припустимо, що axlim
n
n
=
∞→
і bxlim
n
n
=
∞→
, при чому
a≠b.
Виберемо
.ba
3
1
−=ε
Згідно з означенням границі послідов-
ності виконуються нерівності
ba
3
1
ax
n
−<− для ,Nn
1
>
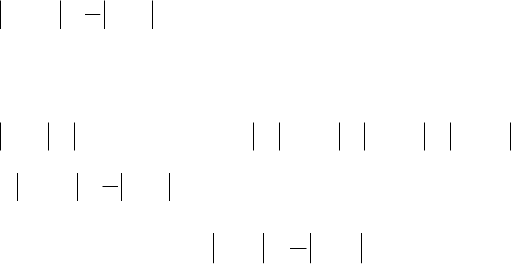
188
ba
3
1
bx
n
−<− для .Nn
2
>
Візьмемо тепер натуральне число
N
, більше за N
1
і N
2
.
Отже, для
n>N одночасно будуть виконуватися обидві вище
написані нерівності, на основі яких одержуємо
.ba
3
2
bx
axbxxa)bx()xa(ba
n
nnnnn
−<−+
+−=−+−≤−+−=−
Звідси знаходимо, що
ba
3
2
ba −<−
, а це неможливо, якщо
.ba ≠ Таким чином, наше припущення, що послідовність може ма-
ти різні границі, привело до протиріччя. Збіжна послідовність може
мати тільки одну границю. Теорема 1 доведена.
ТЕОРЕМА 2. Нехай послідовності (
x
n
) і (y
n
) мають відпо–
відно границі
a і b Тоді сума (x
n
+y
n
) (різниця (x
n-
- y
n
)) має грани-
цю, яка дорівнює
ba +
)ba( −
, тобто
baylimxlim)yx(lim
n
n
n
n
nn
n
±=±=±
∞→∞→∞→
. (3.7)
ТЕОРЕМА 3. Нехай послідовності
)x(
n
і )y(
n
мають від-
повідно границі
a
і
.b
Тоді і їх добуток )yx(
nn
⋅ має границю,
яка дорівнює
ba⋅
, тобто
.baylimxlim)yx(lim
n
n
n
n
nn
n
⋅=⋅=⋅
∞→∞→∞→
(3.8)
З теореми 3 випливають такі наслідки .
1. Сталий множник можна винести за знак границі.
Справді, нехай Cx
n
= , а
n
y має границю. Тоді
n
n
n
n
n
n
nn
n
ylimCylimxlim)yx(lim
∞→∞→∞→∞→
=⋅=⋅
. (3.9)
2. Якщо
axlim
n
n
=
∞→
і k - натуральне число, то
.a)x(limxlim
kk
n
n
k
n
n
==
∞→
∞→
ТЕОРЕМА 4. Нехай послідовності
)x(
n
і
)y(
n
мають скі-
нчені границі, які відповідно дорівнюють
axlim
n
n
=
∞→
,
bylim
n
n
=
∞→
причому
.0b ≠ Тоді і їх відношення
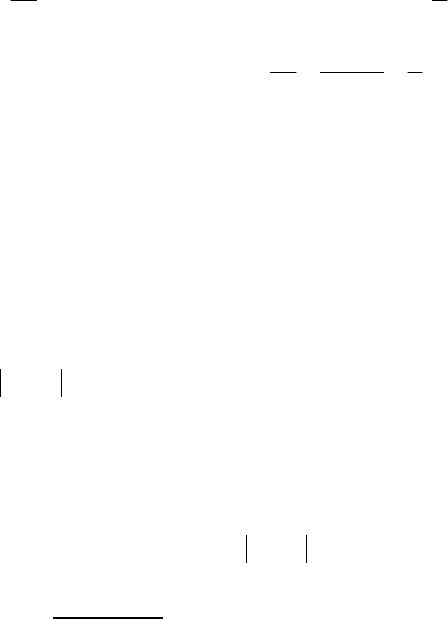
189
)
y
x
(
n
n
має скінчену границю, яка дорівнює
b
a
, тобто
b
a
ylim
xlim
y
x
lim
n
n
n
n
n
n
n
==
∞→
∞→
∞→
. (3.10)
ТЕОРЕМА 5. Послідовність
)x(
n
, яка має границю, є об-
межена.
ТЕОРЕМА 6. Нехай члени послідовностей
)x(
n
,
)y(
n
,
)z(
n
при всіх значеннях
,...2,1n = задовольняють нерівності
nnn
zyx ≤≤
і azlimxlim
n
n
n
n
==
∞→∞→
. Тоді aylim
n
n
=
∞→
.
Доведення. Оскільки число
a
є границею послідовності )x(
n
,
то згідно означення границі послідовності для будь-якого
0>ε іс-
нує таке число, наприклад
1
N
, що для всіх
1
Nn ≥
виконується
ε<− ax
n
або ε+<<ε− axa
n
,
1
Nn ≥ .
Аналогічно існує таке число, наприклад,
2
N , що при
2
Nn ≥
ε+<<ε− aza
n
,
2
Nn ≥
.
Тоді, взявши число
N
більше за
1
N
і
2
N
і використавши умо-
ву теореми 6 та попередні нерівності, дістанемо
ε+<<ε− aya
n
при
n
≥
N, що рівносильно
ε<− ay
n
при n
≥
N.
Остання нерівність й доводить теорему 6.
Означення. Нехай (x
n
) задана послідовність і (n
k
) - довільна
зростаюча послідовність натуральних чисел, то послідовність
)x(
k
n
називається підпослідовністю послідовності (x
n
).
З означення границі послідовності випливає правильність тве-
рдження.
ТЕОРЕМА 7. Якщо послідовність
)x(
n
має границю
a
, то
й будь-яка її послідовність має ту саму границю
a
.
Справді, якщо число
a
є границею послідовності )x(
n
, то
для будь-якого числа
0>ε в ε - окіл
)a,a( ε+ε−
точки
a
потрап-
ляють всі члени цієї послідовності, починаючи з деякого номера
.N
Проте, тоді в цей окіл потрапляють і всі члени послідовності
)x(
k
n
як тільки
.Nn
k
> А це означає, що число
a
є границею
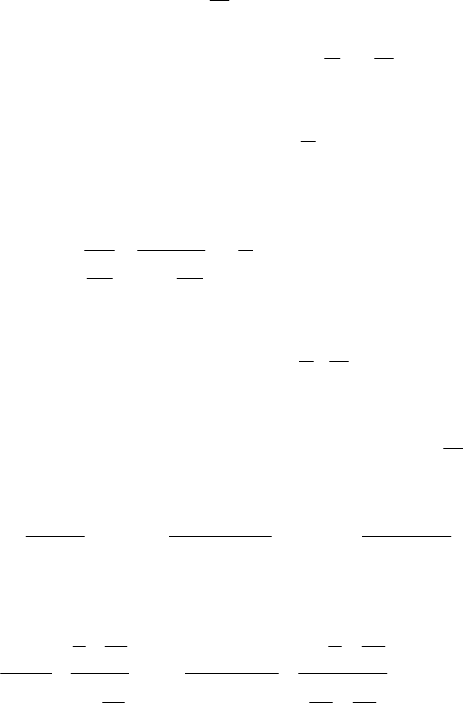
190
послідовності )x(
k
n
, тобто axlim
k
n
k
=
∞→
.
Примітка
1. Враховуючи (3.8) і (3.9), маємо таке твердження:
сталий множник виноситься за знак границі, тобто
.xlimCCxlim
n
n
n
n ∞→∞→
= (3.11)
Примітка
2 У вищій математиці, якщо у граничному переході
вигляду (3.10) одержується дія
∞
a
, то кажуть, що дія допустима і в
результаті одержуємо нуль. Наприклад,
.0)
1
(
n
1
lim
n
=
∞
=
∞→
З другої сторони будемо вважати , якщо у граничному
переході вигляду (3.10) одержується дія
)
0
a
( , 0a ≠ , то
результатом такого граничного переходу є відповідь нескінченість.
Наприклад,
.)
0
1
(
n
1
lim
1
n
1
1
limnlim
2
n
2
n
2
n
∞====
∞→
∞→∞→
Примітка
3. Якщо при граничних переходах (3.8)-(3.10) оде-
ржуються вирази такого вигляду:
,0;;
0
0
; ∞⋅
∞
∞
∞−∞
то такі вирази
будемо називати невизначеними.
3.4. Деякі правила розкриття невизначеностей (
∞
∞
)
Наприклад, нехай потрібно знайти границі :
1)
;
nn
3n
lim
3
2
n
+
−
∞→
2)
;
nn
nnn
lim
2
45
n
+
++
∞→
3)
27
7
n
nn
1nn
lim
+
++
∞→
.
Розділивши чисельник і знаменник на найвищий степінь
n
у
даних прикладах, одержуємо:
1)
;
n
1
1
n
3
n
1
nn
3n
2
3
3
2
+
−
=
+
−
2)
;
n
1
n
1
n
1
n
1
1
nn
nnn
43
4
2
45
+
++
=
+
++
