Шинкарик М.І. Вища математика

Подождите немного. Документ загружается.

171

Означення 1. Інтервалом називається множина всіх чисел

(точок), які знаходяться між двома якими-небудь числами (точ-

ками), що називаються кінцями інтервалу.

Інтервал з кінцями

= і bx = , де ba < , можна задати нері-

вностями

bxa << або записати

()

.b,a

Якщо разом з множиною точок інтервалу розглядати і його

кінці, то одержимо замкнений інтервал або відрізок . Замкнений ін-

тервал з кінцями

= і bx = задається нерівностями bxa ≤≤ ;

його позначають так:

[]

.b,a Інтервал )b,a( називається відкритим,

а інтервали

[

)(

]

b,a,b,a

піввідкритими.

Множину дійсних чисел, що задовольняє нерівність

по-

значають

()

+∞,a

, а множину чисел, що задовольняють нерівність

≥ позначають символом

[

)

+∞,a .

Ми будемо розглядати також числові інтервали

)a,(−∞ , тоб-

то множину чисел таких, що

< і

(

]

a,∞− , якщо

≤ .

Множину всіх дійсних чисел

будемо називати числовим

інтервалом

),( +∞−∞

, якщо +∞<<∞−

Зауважимо, що більшість понять у математиці вводиться за

допомогою означень. Наприклад, квадрат можна означити як пря-

мокутник, у якого всі сторони рівні між собою. Тут більш вузьке

поняття - квадрат означається через посередництво іншого більш

широкого поняття - прямокутника. Зрозуміло, що дати строге озна-

чення всіх понять, які є в математиці, неможливо.

Деякі найбільш

загальні поняття (первісні) слід засвоїти не за допомогою означень,

а іншим шляхом. До таких понять належить поняття множини. Це

поняття засвоюємо, розглядаючи приклади. Так можна говорити про

множину всіх міст певної конкретної країни, про множину всіх сту-

дентів деякого факультету, про множину чисел, які наведені вище у

даному пункті

. Множини позначають великими буквами: С,В,А та

ін. Кожна множина складається з елементів, які позначають малими

буквами:

y,x,c,b,a

та ін. Наприклад, число 21 є елемент множини

всіх натуральних чисел. Те, що елемент

належить множині

за-

писують так:

Xx ∈ . Якщо елементи

не належать множині

, то

записують

Xx∉

Нехай дано дві множини

. Якщо кожний елемент мно-

жини

є одночасно й елементом множини В , то кажуть, що мно-

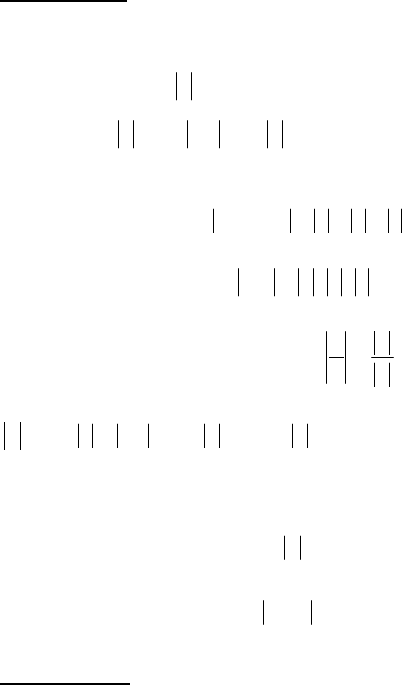
172

жина

є підмножиною В , і записують

⊂ або

⊃ .

Якщо

⊂

, то кажуть, що множини

рівні і

записують

.BА =

У математиці розглядають і так звану порожню множину, яка

не містить жодного елемента. ЇЇ позначають знаком Ø. Наприклад,

множина всіх дійсних коренів рівняння

01x

=+ є порожня мно-

жина (рівняння

01x

=+ немає дійсних коренів).

1.3. Абсолютна величина дійсного числа

Означення 2. Абсолютною величиною (або модулем) дійсно-

го числа

називається саме число

, якщо

додатне і число -

, якщо

від’ємне.

Абсолютна величина

оа =

приймається

рівною 0 і позначають

⎩

⎨

⎧

<−

≥

а,а

,0а,а

Наприклад,

,33 =

33 =−

00 =

◙ Властивості абсолютної величини

1. Абсолютна величина алгебраїчної суми не більша суми аб-

солютних величин , тобто

.cbacbа ++≤−+

2. Абсолютна величина добутку дорівнює добутку абсолют-

них величин множників :

.cbaаbc ⋅⋅=

3. Абсолютна величина частки дорівнює частці від ділення аб-

солютних величин діленого і дільника :

, якщо

0b ≠

4. Для будь-якого

правильні співвідношення:

;0a ≥

;aa −=

;aa ≤

.aa ≤−

1.4. Властивості абсолютної величини, зв’язаної з нерівно-

стями величин. Окіл точки

1. Нехай

0>α . Нерівність α<x рівносильна нерівностям

α<<α−

2. Нехай

0>α

. Нерівність

α<− ax

рівносильна

нерівностям

α+<<α−

Означення 3. Околом точки

називається кожен інтер-

вал вигляду (

α+α−

), де 0>α .

173

Таким чином, запис α<− ax , 0>α , означає множину чисел

, що знаходяться в околі точки

1.5. Верхня і нижня грані дійсних чисел

Нехай дано непорожню множину

дійсних чисел

(

).R⊂ Множина

називається обмеженою зверху (знизу), якщо

існує дійсне число

таке, що для всіх

правильна нерівність

)x(x α≥α≤ .

Число

α при цьому називається верхньою (нижньою) межею

множини

. Зрозуміло, що коли α -верхня (нижня) межа множини

, то будь-яке число α>

)( α<

також буде верхньою (ниж-

ньою) межею.

Означення 4. Найменша верхня межа непорожньої обме-

женої зверху множини

дійсних чисел називається точною

верхньою межею або верхньою гранню цієї множини і познача-

ється sup

{}

Означення 5.

Найбільша нижня межа непорожньої обме-

женої знизу множини дійсних чисел

називається точною

нижньою межею або нижньою гранню цієї множини і познача-

ється inf

{}

Наприклад, якщо

⎭

⎬

⎫

⎩

⎨

⎧

= ,...

,...,

,1X

, то sup

{}

=1,

inf

{}

X =0.

Тут верхня грань, яка дорівнює 1, належить множині

нижня грань, яка дорівнює 0, множині

X не належить. Коли у

множині

є найбільше (найменше) число

, тобто таке число

∈

, що будь-яке число x ∈

задовольняє нерівність

xx ≤

)xx(

≥

, то це число

й буде верхньою (нижньою) гранню мно-

жини

. Однак не в усякій непорожній обмеженій зверху (знизу)

множині дійсних чисел є найбільше (найменше ) число. Наприклад,

у розглянутій вище множині

⎭

⎬

⎫

⎩

⎨

⎧

= ,...

,...,

,1X

є найбільше чи-

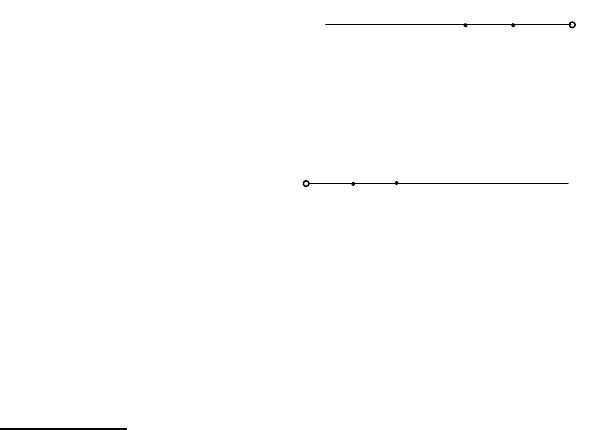
174

сло, але немає найменшого, а у множині

()

b,aX

немає ні най-

меншого, ні найбільшого числа.

Сформулюємо без доведення наступне твердження.

ТЕОРЕМА 1. У будь-якої непорожньої обмеженої зверху

(знизу) множини

дійсних чисел існує верхня (нижня) грань.

Надалі нам доведеться часто користуватися наступними двома

властивостями

sup

{}

X і inf

{}

X .

Властивість 1



. Якщо

- непорожня обмежена зверху

множина дійсних чисел і

{}

Xsup=α

, то для будь-якого

x ∈

правильна нерівність α≤

і для будь-якого числа 0>ε іс-

нує число

∈

таке, що .x ε−α>

Властивість 2



. Якщо

- непорожня обмежена знизу мно-

жина дійсних чисел і

{}

Xinf=

, то

1) для будь-якого

x ∈

правильна нерівність

≥x

;

2) для будь-якого числа

0>ε існує число

x ∈

таке, що

.x ε+

Зазначимо, що коли множина дійсних чисел необмежена звер-

ху (знизу), то за означенням

{}

+∞=Xsup

{}

).Xіnf( −∞=

§2. Класифікація функцій

2.1. Поняття функції. Способи задання функції

Означення 1. Нехай

- дві числові множини. Якщо

кожному значенню

∈

за деяким правилом (законом) f по-

ставимо у відповідність одне дійсне число

∈

, то будемо гово-

рити , що на множині

задано функцію f .

Множина

)f(DD =

називається областю визначення

функції, а множина

{}

Dx),x(f)D(fE ∈== - називається облас-

тю значень функції,

х – називається аргументом функції.

Функції позначаються малими буквами латинського

алфавіту

v,u,h,q,f

і т.д.

α-ε

(

β+

)

175

Але для простоти вивчення курсу вищої математики надалі ми

будемо використовувати такі формулювання і позначення функцій:

нехай задано функції

)x(vv),x(uu),x(yy === і т.д.

Основними способами задання функції є такі: аналітичний,

табличний, графічний, словесний.

Функція, задана аналітично, якщо вона задана за допомогою

однієї або кількох формул. Табличний спосіб полягає в тому, що

функцію задають за допомогою таблиці, яка містить ряд окремих

значень аргументу

і відповідні їм значення функції.

Графічний спосіб задання функції полягає в тому, що її пода-

ють на малюнку у вигляді певної кривої, що задає множину точок

{}

)x(f,x , яку називають графіком функції.

Якщо функцію не можна задати першими трьома спосо-

бами, то її описують за допомогою висловлень (опису). В цьо-

му полягає словесний спосіб задання функції.

2.2. Класифікація функцій

) Обмежені функції:

Означення 2. Функція )x(fy = , яка визначена на множині

називається обмеженою зверху (знизу), якщо існує число

таке, що для всіх

∈

виконується нерівність M)x(f ≤

(

M)x(f ≥

Якщо функція

)x(fy = , обмежена на множині

і зверху і

знизу, то вона називається обмеженою на всій множині

Наприклад, функція

xsiny =

обмежена на всій числовій осі,

1xsin ≤ для

∈ (

),∞∞−

) Монотонні функції:

Означення 3. Функція )x(fy = , яка визначена на множині

називається: а) зростаючою; б) спадною; в) незростаючою; г)

неспадною на цій множині, якщо для будь-яких

х і

x , які на-

лежать множині

і при

мають місце відповідні нерів-

ності

: а) );x(f)x(f

< б) );x(f)x(f

> в) );x(f)x(f

≥

г)

).x(f)x(f

≤

Функції, які задовольняють даному означенню, нази-

вають монотонними.

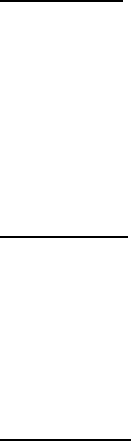
176

в) Парні і непарні функції:

Означення 4. Функція )x(fy = називається парною, якщо

для будь-яких

∈

{}

axa <<−

виконується умова

)x(f)x(f =− і непарною, якщо ).x(f)x(f −=−

Наприклад,

xy = - парна функція,

xy = - непарна функція.

Зауважимо, що графік парної функції симетричний відносно осі

Оу

а графік непарної функції - симетричний відносно початку коорди-

нат.

) Періодичні функції:

Означення 5. Функція )x(fy = , яка визначена на всій чис-

ловій осі називається періодичною, якщо існує таке число

,0T ≠

яке називається періодом, що має місце нерівність

)x(f)Tx(f =+ для всіх x∈ ).,( +∞−∞

Наприклад,

.2T,xcos)2xcos( π==π+

Функція

cos

= є періодична з періодом π2 .

) Складні функції:

Означення 6. Нехай функція

)u(fy =

визначена на мно-

жині

U , а функція )x(u

= визначена на множині

і всі її зна-

чення

∈

U . Тоді змінна

через проміжну змінну

є функцією

)).x((fy

В цьому випадку

є складною функцією або

функцією від функції.

Наприклад,

uy = ,

cos

= Тоді xcosy

= є складною фу-

нкцією

) Обернені функції:

Нехай функція

)x(fy =

задана на множині

, а множина

значень (область зміни функції ) є

. Якщо кожному значенню

∈

відповідає одне значення

∈

, для якого

)x(fy =

, то на

множині

можна визначити функцію )y(fx

1−

= так, що кожному

значенню

∈

буде відповідати одне значення

∈

, для якого

.y)x(f =

Функція

)y(fx

1−

називається оберненою відносно

функції

)x(fy = , яка задовольняє для всіх

∈

умові

)).y(f(fx

1−

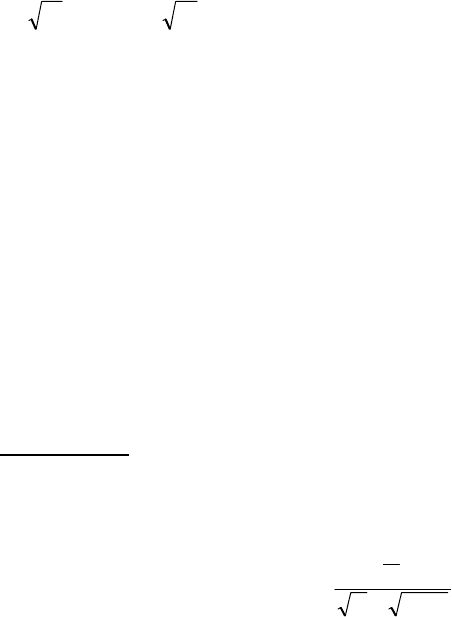
177

Приклад. Нехай задана функція

xy = ,

∈

[

)

D,0 =+∞

∈

[

)

+∞,0

. Оберненою для даної функції буде фун-

кція

.yx = ,y)y(f

−

∈

[

)

+∞,0 .

) Неявна функція від однієї змінної.

Якщо функція задана не рівнянням вигляду

)x(fy = , а рів-

нянням вигляду

0)y,x(F = , то у припущенні, що на деякій мно-

жині рівняння

0)y,x(F =

має єдиний розв’язок

)x(yy =

, тоді

рівність

0)y,x(F = називають неявним заданням функції.

Наприклад,

xy =

cos

- явні функції, а рівняння

01y5x =−+

визначає неявну функцію

від

) Елементарні функції.

Cтепенева функція

= xy

, показникова

ay = , логарифмічна

xlogy

= ,тригонометричні ,xsiny =

cos

= ,

tgx

ctgx

обернені тригонометричні

,xarcsiny =

arccos

arctgx

arcctgx

і стала Cy = називаються основними елементарними

функціями.

Означення 7. Основні елементарні функції, а також функ-

ції, знайдені за допомогою формул, що містять лише скінчене

число арифметичних дій (+,-,

) і суперпозицій основних елеме-

нтарних функцій, називаються елементарними функціями.

Наприклад,

3x2arcsin

xsinx

tgx

cos2

)5xx(siny

−

+−+=

- елементарна функція.

Елементарні функції поділяються на такі класи:

1)Цілі раціональні функції:

Цілі раціональні функції – це функції вигляду

a...xaxay +++=

−

, де −= )n,...,2,1,0k(a

сталі дійсні числа.

Такі функції називаються ще многочленами, а числа

a - коефіцієн-

тами многочлена; якщо

≠

, то число

називають степенем

многочлена.

2) Раціональні функції:

Раціональні функції – це функції вигляду

178

bxb...xbxb

axa...xaxa

m1m

n1n

++++

−

тобто це частка двох цілих

раціональних функцій (многочленів).

Якщо

0m ≠ ,

≠

, то раціональна функція називається

дробово-раціональною.

3)Ірраціональні функції:

Ірраціональні функції - це функції, які задані за допомогою

суперпозицій раціональних функцій, степеневих функцій з раціона-

льними показниками і чотирьох арифметичних дій, застосованих

скінчене число раз. Наприклад,

- ірраціональна фун-

кція .

4) Алгебраїчні функції:

Функція

від

(

))x(yy =

називається алгебраїчною, якщо

вона задовольняє рівняння

,0)x(PyP...y)x(Py)x(P

n1n

=++++

−

де P

(x),(

)n,...,2,1,0k =

- алгебраїчні многочлени від

Всяка раціональна функція є алгебраїчною, оскільки

0)x(Py)x(P

, де

,b...xb)x(P

++=

).a...xa()x(P

++−=

5)Трансцендентні функції:

Елементарні функції, які не є алгебраїчними, називаються

трансцендентними елементарними функціями. Можна показати, що

тригонометричні, обернено тригонометричні, показникова і логари-

фмічна функції є трансцендентними елементарними функціями.

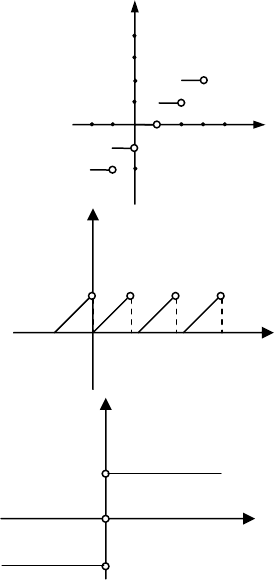
6) Деякі неелементарні функції:

xy = - абсолютне значення, або

модуль,числа

179

[]

xy =

– ціла частина числа

{}

xy =

– дробова частина чис-

ла

⎪

⎩

⎪

⎨

⎧

<−

0x,0

,0x,1

xsigny

- знак числа

2.3. Криві попиту і пропозиції. Точка рівноваги

Розглядаючи попит

Q і пропозицію S в залежності від ціни

на вироблений товар, зрозуміло, що чим менша ціна на товар, то

більший попит при певній купівельній спроможності населення , і

навпаки, якщо ціна на товар зростає, то пропозиція зростає.

Як правило, залежність попиту

Q від ціни

має вигляд:

cPQ +=

, ,0<α

const

, а залежність пропозиції S від ціни

має вигляд:

dPS +=

, ,1≥α constd = .

Константи

і d називаються екзогенними величинами і за-

лежать від зовнішніх причин ( благополуччя населення, політичної

ситуації, пори року і т.д.).

-1

-2

2 3 4

-1

-2

-1

-2

-1

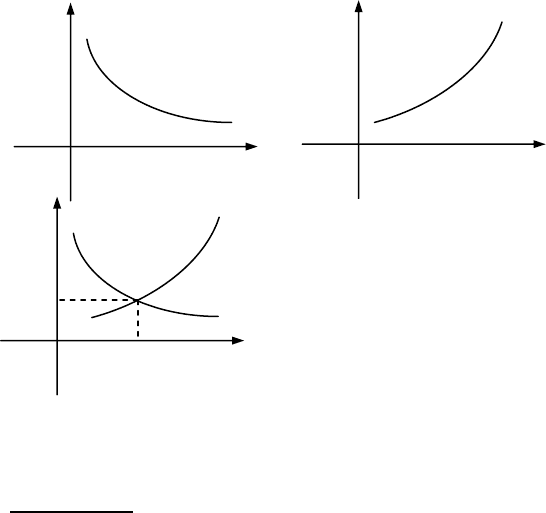
180

Графіки даних функцій мають вигляд:

При розв’язуванні економічних

задач цікаво знати умову рівнова-

ги попиту і пропозиції

)Р(S)Р(Q( = , тобто рівноваж-

ну ціну

§ 3. Границя числової послідовності

3.1. Числова послідовність

Означення 1. Кожна функція f визначена на множині на-

туральних чисел

{}

,...n,...,3,2,1N =

називається числовою послі-

довністю

Запишемо значення функції

),...n(f),...,3(f),2(f),1(f (3.1)

Введемо позначення

)n(fx

= ,n ∈N. (3.2)

Отже, числову послідовність (3.1) можна записати так :

,...,x,...,x,x,x

n321

або скорочено

( ),x

n ∈N , (3.3)

де

,...x,x

називають членами послідовності, а

- “енним ” або

загальним членом числової послідовності.

Якщо задана послідовність у такому вигляді

n ∈N , (3.4)

то задано закон утворення її членів, тобто надаючи номеру

значень

,...3,2,1 можна однозначно визначити всі її члени

S,Q