Шинкарик М.І. Вища математика
Подождите немного. Документ загружается.


141
6) Аналогічно, коли 0BD == , 0C,0A ≠≠ , то рівнянню
0CzAx =+
відповідає площина , що проходить через вісь y0 .
7) Коли
0B,0C,0AD ≠≠== , то рівнянню 0CzBy =+
відповідає площина, що проходить через вісь
x0 .
8) Якщо
0D,0C,0BA ≠≠== , то рівняння 0DСz =+
визначає площину , яка паралельна вісі
x0
і вісі y0 , тобто площина
паралельна координатній площині
xy0 . Ця площина відтинає на осі
z0 відрізок
C
D
z
−= .
9) Аналогічно, коли
0D,0B,0CA ≠≠==
, то рівняння
0DBy =+ визначає площину , яка паралельна координатній пло-
щині
xz0 і відтинає на вісі
y0
відрізок
.
B
D
y −=
10) Коли
,0CB ==
0A ≠ , 0D ≠ , то рівняння 0DAx =+ ви-
значає площину, яка паралельна координатній площині
yz0
і відти-
нає на вісі
x0 відрізок
A
D
x
−= .
11) Якщо
,0A,0DCB ≠=== то рівняння
0Ax =
рівно-
сильне
0x = , а це і є рівняння координатної площини yz0 .
12) Аналогічно, коли
0B,0D,0C,0A ≠=== , то рівняння
,0By =
(
0y =
) представляє відповідно координатну площину .zx0
13) Якщо
,0C,0DBA ≠===
то рівняння 0C = (або )0z =
є відповідно рівнянням координатної площини
Oxy.
17.2. Рівняння площини у відрізках
Нехай в рівнянні (2.72) кожний із коефіцієнтів
D,C,B,A
не
дорівнює нулю, тобто площина перетинає всі осі координат і не
проходить через початок координат. Перетворимо рівняння (2.72)
таким чином:
,DCzByAx −=++
,1z
D
C
y
D
B
x
D
A
=
−
+
−
+
−

142
.1
C
D
z
B
D
y
A
D
x
=
−
+
−
+
−
Для скорочення запису позначимо
,с
C
D
,b
B
D
,a
A
D
=−=−=−
тоді рівняння площини буде мати
вигляд
1
c
z
b
y
a
x
=++ . (2.73)
Рівняння (2.73) називають рівнянням площини у відрізках, де
числа
c,b,a є величини відрізків, які відтинає площина на осях ко-
ординат.
17.3. Кут між двома площинами. Умови паралельності
і перпендикулярності площин.
Нехай задано дві площини
0DzCyBxA
1111
=+++ , (2.74)
0DzCyBxA
2222
=+++ . (2.75)
Якщо ці площини перетинаються, то кутом між ними назвемо
будь-який суміжний двогранний кут. Один із них дорівнює куту
ϕ
між векторами
)C,B,A(n
111
1
→
і
)C,B,A(n
222
2
→
, а другий -
ϕ−=ϕ
0
1
180
.
Значить, шуканий кут φ можна знайти за формулою (2.21) §11
2
2
2
2
2
2
2
1
2
1
2
1
212121
CBACBA
CCBBAA
cos
++++
++
=ϕ
. (2.76)
Якщо
,
2
π
=ϕ то із формули (2.76) одержуємо, що
0CCBBAA
212121
=++ . (2.77)
Умова (2.77) одержується із умови перпендикулярності векто-
рів
1
n
→
і
2
n
→
. Рівність (2.77) називається умовою перпендикулярності
двох площин.
Якщо площини (2.74) і (2.75) паралельні, то нормалі цих пло-
щин
)C,B,A(n
111
1
=
→
і )CB,A(n
2,22
2
=
→
будуть колінеарні і тоді за
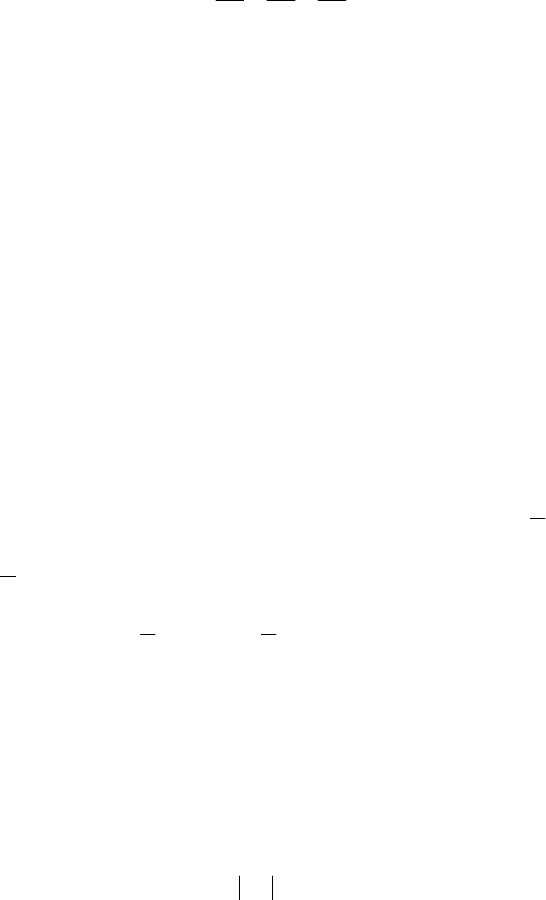
143
формулою (2.23) одержимо
2
1
2
1
2
1
C
C
B
B
A
A
==
. (2.78)
Умова (2.78) виражає умову паралельності двох площин.
Приклад 1. Записати рівняння площини, що проходить через
точки
)1;3;8(M
1
−
і
)2;7;4(M
2
і перпендикулярна до площини
02172y5x3 =+−+ .
Розв
’язування. Тому що площина проходить через точку
)1;3;8(М
1
− , то її координати задовольняють рівняння (2.71), тобто
0)1z(C)3y(B)8x(A =−+++−
. (2.79)
Аналогічно, площина проходить і через точку
)2;7;4(M
2
, то
її координати задовольняють рівнянню (2.79), тобто
0)12(C)37(B)84(A =−+++− . (2.80)
Використаємо умову перпендикулярності (2.77) для площини
(2.79) і заданої площини
3x+5y-7z+21=0, тобто 3A+5B-7C=0. Для
знаходження
А,В,С маємо систему двох рівнянь з трьома невідоми-
ми, а саме
⎩
⎨
⎧
=−+
=++−
.0C7B5A3
,0CB10A4
З даної системи знаходимо
A
і
B
через C , тобто ,C
2
3
A =
C
2
1
B =
і підставляємо одержані значення в рівняння (2.79):
.0)1z(C)3y(
2
1
)8x(C
2
3
=−+++−
Зробивши спрощення в останньому рівнянні , одержуємо шу-
кане рівняння площини
3x+y+2z-23=0.
17.4. Нормальне рівняння площини
Положення площини
π в просторі можна визначити через нор-
мальний вектор
→→
= OAn
, початок якого співпадає з початком коор-
динат, а кінець знаходиться на площині π. Нехай довжина цього ве-
ктора дорівнює
p
, тобто
→
= ОАp , а кути нахилу цього вектора з
осями координат є α,β,γ (мал.45). Значить
р є віддаль площини до
144
початку координат. Якщо через
→
0
n позначимо одиничний вектор
нормалі
→→
= OAn , то коорди-
нати
→
0
n будуть
(
cosα,cosβ,cosγ). На основі
§8 їх називають направляю-
чими косинусами нормаль-
ного вектора. Візьмемо до-
вільну точку
)z,y,x(M
на
площині
π і позначимо ра-
діус - вектор
→
OM
через
→
r
.
Тоді
prПp
0
n
=
→
→
. Тепер на основі формули (2.15) маємо
→
→
→
→
→
→
⋅=
⋅
=
→
,nr
n
nr
rПp
0
0
0
n
0
бо
.1n
0
=
→
Значить, ми одержимо, що
pnr
0
=⋅
→
→
або
0pnr
0
=−⋅
→
→
. (2.81)
Рівняння (2.81) називається нормальним рівнянням площини у
векторній формі. Розпишемо рівняння (2.81) у координатній формі,
одержимо
0pcoszcosycosx =−
γ
+
β
+α . (2.82).
В цьому рівнянні
p
віддаль від площини до початку координат і
1coscosсos
222
=γ+β+α . (2.83)
Щоб загальне рівняння площини привести до нормального ви-
гляду, потрібно загальне рівняння площини помножити на сталий
множник
μ
. Одержимо
0DCzByAx =
μ
+
μ
+
μ
+
μ
, де
α=
μ
cosA
,
β
=
μ
cosB ,
γ
=
μ
cosC , pD −=
μ
.
Піднісши перші три рівності до квадрату і додавши їх, врахо-
вуючи (2.83), одержимо
1)CBA(
2222
=++μ
, або
222
CBA
1
++
±=μ
. (2.84)
γ
α
β
→
r
π
M(х,у,z)
A
0
n
→
O
z
у
х
Мал.45
145
В формулі (2.84) необхідно брати знак протилежний знаку ві-
льного члена в загальному рівнянні площини, так як
pD −=
μ
, де
p
- завжди додатне як віддаль.
Отже, щоб рівняння (2.72) привести до нормального вигляду ,
треба помножити його на нормувальний множник (2.84).
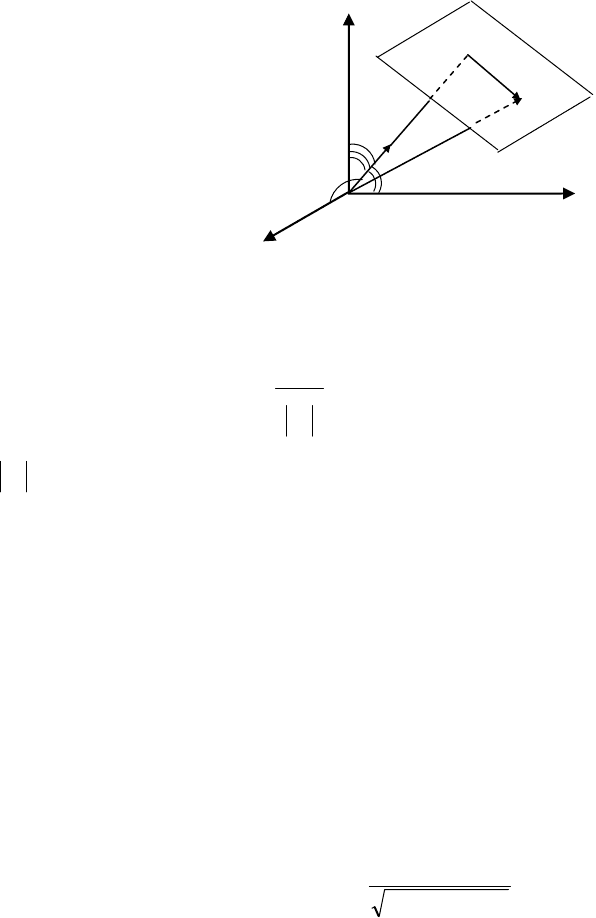
17.5. Віддаль від точки до площини
Нехай задано нормальне
рівняння площини
π :
0pcoszcosycosх =−
γ
+
β
+α
і точка
)z,y,x(M
0000
поза
площиною. Потрібно обчислити
віддаль від точки
0
M
до пло-
щини
π . (мал. 2.46).
Розв
’язування. Проведемо
через точку
0
M
площину
1
π
паралельну до площини
π
(мал.
46). Нормальне рівняння пло-
щини
1
π
запишемо так
0pcoszcosycosx
1
=−
γ
+
β
+α
де
1
p
віддаль площини
1
π
від по-
чатку координат. Шукана віддаль дорівнює
ppAB
1
−= . Тому що
точка
)z;y;x(M
0000
знаходиться на площині
1
π
, то
0pcoszcosycosx
1000
=−
γ
+
β
+α
і значить
pcoszbcosycosxppd
0001
−
γ
++α=−= . Взагалі
pcoszcosycosxd
000
−γ+β+α=
(2.85)
або
222
000
CBA
DCzByAx
d
++
+++
=
. (2.86)
§18. Пряма в просторі
В просторі, так як і на площині, одну і ту ж пряму можна за-
дати різними по формі рівняннями.
х
В
А
р
1
р
π
π
1
O
z
у
Мал.46
М
0
146
18.1. Загальне рівняння прямої
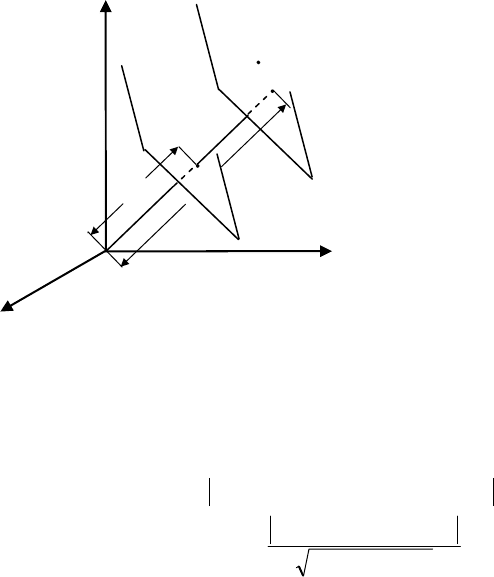
Пряму
l в просторі можна розглядати як лінію перетину двох
площин
1
π і
2
π (мал.47). Тому загальним рівнянням прямої l є си-
стема двох рівнянь першого степеня , а саме
⎩
⎨
⎧
=+++
=+++
.0DzCyBxA
,0DzCyBxA
2222
1111
(2.87)
Координати прямої
l бу-
дуть задовольняти обом рівнян-
ням системи (2.87). Система
(2.87) визначає пряму лінію
l
при умові, що нормальні вектори
)C,B,A(n
1111
→
і
)C,B,A(n
2222
→
неколінеарні, бо тільки в цьому
випадку площини перетинають-
ся.
18.2. Канонічне рівняння прямої
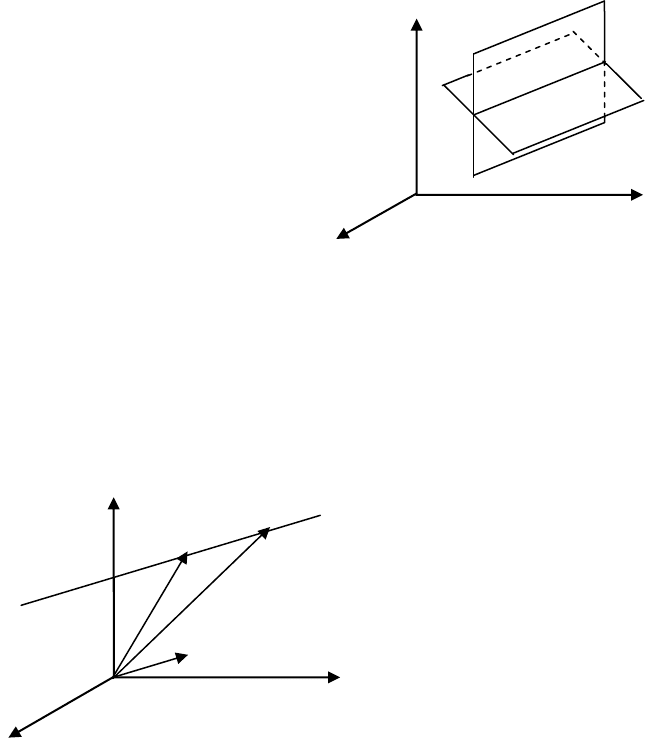
Положення прямої лінії в просторі визначається однозначно,
якщо відома точка
M
0
(x
0
y
0
z
0
,) ,через яку вона проходить , і відомо
напрямний вектор
)p;n;m(s
→
, якому пряма l паралельна (мал.48).
Візьмемо на прямій
l довільну точку
)z;y;x(M
і позначимо
→
OM
через
→
r
, а вектор
→
0
OM
через
.r
0
→
З малюнка (48) видно , що
→→→
+= MMOMOM
00
,
або
→→→
+= MMrr
00
. (2.88)
Вектор
→
MM
0
коліне-
арний із направляючим век-
тором
→
s , тому
→→
⋅= stMM
0
, (2.89)
де
t
- числовий параметр.
Тоді (2.88) запишемо у вигляді
→→→
⋅+= strr
0
. (2.90)
π
1
π
2
l
O
z
у
х
Мал.47
→
r
0
r
→
→
s
M
M
0
l
O
z
у
х
Мал
.4
8

147
Рівняння (2.90) називається векторним рівнянням прямої в
просторі. Розпишемо рівняння (2.90) в координатній формі
ptzz,ntyy,mtxx
000
+=+=+=
. (2.91)
Рівняння (2.91) називаються параметричними рівняннями
прямої. Якщо параметр
t
змінюється, то точка )z;y;x(M рухаєть-
ся по прямій
.l
Виключивши параметр
t
із рівнянь (2.91) , одержимо
.
p
zz
t,
n
yy
t,
m
xx
t
000
−
=
−
=
−
= Звідси
p
zz
n
yy
m
xx
000
−
=
−
=
−
. (2.92)
Рівняння (2.92) називаються канонічними рівняннями прямої
в просторі, а координати
n
,
m
і
p
вектора
→
s
- направляючими кое-
фіцієнтами прямої.
В канонічних рівняннях (2.92) величини
n
,
m
і
p
не можуть
одночасно перетворюватися в нуль, так як
0s ≠
→
, але деякі із них
можуть дорівнювати нулю.
Нехай, наприклад,
0m = , то із рівнянь (2.91) одержимо таку
систему
⎪
⎭
⎪
⎬
⎫
−
=
−
=
p
zz
n
yy
xx
00
0
(2.93)
Кожне із цих двох рівнянь визначає площину, а система рів-
нянь (2.92) визначає пряму. В цьому випадку рівняння (2.92) можна
записати умовно так:
p
zz
n
yy
0
xx
000
−
=
−
=
−
. (2.94)
Система рівнянь (2.93) або (2.94) визначає пряму, яка перпен-
дикулярна до вісі
x0 , так як 0m = . Якщо які-небудь два направ-
ляючих коефіцієнти рівні нулю, наприклад,
m=0,n=0, p≠0, то із рів-
няння (2.91) одержимо, що
⎭
⎬
⎫
=
=
0
0
yy
xx
(2.95)

148
Рівняння (2.92) умовно запишеться так:
р
zz
0
yy
0
xx
000
−
=
−
=
−
. (2.96)
Пряма, яка визначається системою (2.95), або (2.96) паралель-
на осі
z0
і перпендикулярна до осей
x0
і y0 .
Канонічні рівняння прямої (2.92) можна представити як суку-
пність двох рівнянь, наприклад
p
zz
m
xx
00
−
=
−
і
p
zz
n
yy
00
−
=
−
. (2.97)
Кожне із цих рівнянь представляє площину. Перша площина
паралельна вісі
y0 , так як в рівнянні відсутня координата
y
, а дру-
га паралельна осі
x0 .
Таким чином, пряму можна розглядати як перетин двох пло-
щин, тобто канонічні рівняння прямої (2.92) записали у загальному
вигляді прямої (2.97).
18.3. Рівняння прямої, що проходить через дві задані точки
Нехай пряма проходить через дві задані точки
)z,y,x(M
1111
і
).z,y,x(M
2222
В цьому випадку за направляючий вектор прямої
→
s можна взяти вектор )zz,yy,xx(MMs
12121221
−−−==
→→
. Тоді
121212
zzp,yyn,xxm −=−=−= і взявши за
,zz,yy,xx
101010
===
одержимо
12
1
12
1
12
1
zz
zz
yy
yy
xx
xx
−
−
=
−
−
=
−
−
. (2.98)
Рівняння (2.98) є рівнянням прямої в просторі , що проходить
через дві задані точки.
Загальне рівняння прямої можна привести до канонічних рів-
нянь (2.92). Для цього в системі (2.87), наприклад,
z
надаємо зна-
чення
0
z і система (2.87) буде системою двох рівнянь з двома неві-
домими
x і y, які із неї знаходимо, тобто x=x
0
і x=x
0
. Таким чином,
одержали координати
)z,y,x(
000
однієї точки
0
M в просторі. Ана-
логічно, із системи (2.87) надаючи
1
zz = , знаходимо
149
,yy,xx
11
== тобто координати
)z,y,x(
111
другої точки
1
M
.
Тепер можна записати рівняння прямої, що проходить через дві точ-
ки в просторі на основі (2.98) і одержимо рівняння (2.92).
18.4. Кут між двома прямими
Нехай задано дві прямі
1
l і
2
l :
1
l ⇒
1
1
1
1
1
1
p
zz
n
yy
m
xx −
=
−
=
−
, (2.99)
2
l ⇒
2
2
2
2
2
2
p
zz
n
yy
m
xx −
=
−
=
−
. (2.100)
Означення. Кутом між двома прямими
1
l і
2
l називається
кут між їх направляючими векторами
)p,n,m(s
1111
→
і
)p,n,m(s
2222
→
.
Кут між двома прямими
1
l і
2
l буде визначатися за форму-
лою (2.21) , тобто
2
2
2
2
2
2
2
1
2
1
2
1
212121
pnmpnm
ppnnmm
сos
++⋅++
++
=ϕ
. (2.101)
Очевидно, що
0
1800 ≤ϕ≤
.
Якщо прямі (2.99) і (2.100) паралельні, то їх направляючі век-
тори
→
1
s і
→
2
s колінеарні, то ми одержуємо умову паралельності пря-
мих
1
l і
2
l у вигляді
2
1
2
1
2
1
p
p
n
n
m
m
==
. (2.102)
Умова (2.102) є умовою паралельності прямих
1
l
і
2
l
. Якщо
прямі
1
l
і
2
l
взаємно-перпендикулярні , то направляючі вектори
)p,n,m(s
1111
→
і
)p,n,m(s
2222
→
також перпендикулярні , тобто їх
скалярний добуток
0ss
21
=⋅
→→
. Звідси
0ppnnmm
2121
2
1
=++ . (2.103)
150
Умова (2.103) є умовою перпендикулярності двох прямих
1
l
і
2
l у просторі.
18.5. Взаємне розміщення прямої і площини
Нехай задана пряма
l
p
zz
n
yy
m
xx
000
−
=
−
=
−
(2.104)
і площина
0DCzByAx =+++
. (2.105)
Пряма
l паралельна до площини π тоді і тільки тоді, коли її
направляючий вектор
)p,n,m(s
→
перпендикулярний до нормального
вектора
)C,B,A(n
→
площини. Тоді їх скалярний добуток дорівнює
нулю
0CpBnАm =++ . (2.106)
Умова (2.106) є умовою паралельності прямої і площини.
Якщо пряма
l перпендикулярна до площини π , то направля-
ючий вектор прямої
)p,n,m(s
→
і нормальний вектор площини
)C,B,A(n
→
паралельні, тобто
p
C
n
B
m
A
==
. (2.107)
Умова (2.107) є умовою перпендикулярності прямої і площини.
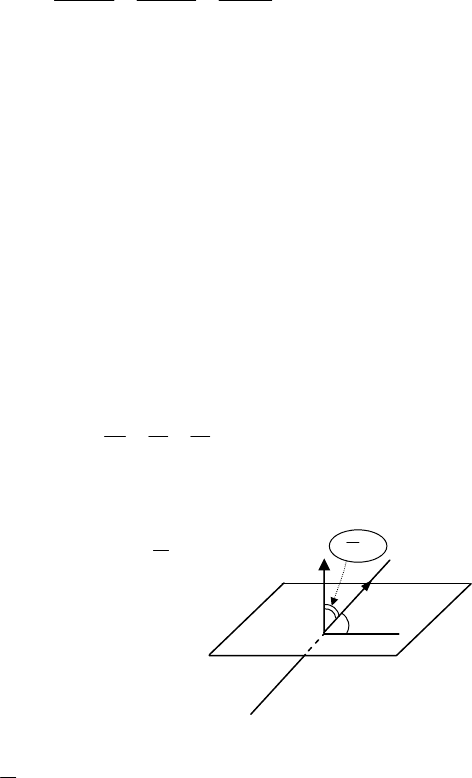
Кутом між прямою
l і площи-
ною
π називається кут
2
0(
π
≤ϕ≤ϕ
),
який утворений прямою
l з її проек-
цією на площину (мал.49). З малюнка
49 видно, що кут між нормальним
вектором
)C,B,A(n
→
площини і на-
правляючим вектором
)p,n,m(s
→
прямої дорівнює
ϕ−
π
2
, а якщо век-
π
→
n
→
s
φ
Мал.49
l
ϕ−
π
2
