Шинкарик М.І. Вища математика
Подождите немного. Документ загружается.

131
16.3.Рівняння прямої, що проходить через дві задані точки
Нехай задано дві точки
)y,x(M
11`1
і )y,x(M
22`2
.
Для одержання рівняння прямої
21
MМ (мал.28) запишемо рівняння пря-
мої, що проходить через точку
)y,x(M
11`1
, а саме )xx(kyy
11
−=− .
Оскільки точка
)y,x(M
22`2
знаходиться на прямій
l
, то підс-
тавивши координати цієї точки в рівняння в’язки прямих(2.53), оде-
ржимо
)xx(kyy
1212
−=− . З цієї рівності знайдемо кутовий коефі-
цієнт прямої
12
12
xx
yy
k
−
−
=
(2.54)
Тепер підставивши вираз для
k , тобто (2.54) в рівняння (2.53)
і одержимо шукане рівняння прямої
12
1
12
1
xx
xx
yy
yy
−
−
=
−
−
(2.55)
Примітка
. Якщо точки
1
М і
2
М лежать на прямій , яка пара-
лельна осі
Oy , тобто
21
xx = , то рівняння прямої буде
1
xx = . Коли
згадані точки лежать на прямій, яка паралельна вісі
Ox , тоді
21
yy =
і рівняння прямої буде
.yy
1
=
Приклад 1. Скласти рівняння прямої, що проходить через то-
чки
)4;3(A −
і
).1;5(B −
Розв
’язування. Використовуючи формулу (2.55), запишемо
)3(5
3x
41
4y
−−
+
=
−−
−
або
8
3x
5
4y +
=
−
−
.
Розкривши пропорцію, маємо
)3х(5)4y(8 +−=− . Спрости-
вши, одержимо
8
17
x
8
5
y +−=
.
16.4. Рівняння прямої у відрізках
Нехай пряма відсікає від початку координат на осі
Ox відрі-
зок
0a ≠ , а на осі
Oy
відрізок 0b ≠ , тоді пряма проходить через дві
точки
)0;a(A і )b;0(B .
М
1
(х
1
,у
1
)
Мал.28
67
х
у
О
М
2
(х
2
,у
2
)
l
132
Використавши формулу (2.55)
для точок
)0;a(A і )b;0(B , одержимо
a
0
ax
0
b
0y
−
−
=
−
−
і після спрощення маємо
1
b
y
a
x
=+
. (2.56)
Рівняння (2.56) називається рів-
нянням прямої у відрізках.
Приклад 2. Скласти рівняння
прямої, що проходить через точку A(1;2), яка відтинає на додатній
осі
Oy відрізок у два рази більший як на додатній осі .Ox
Розв
’язування.У рівності (2.56) за умовою
).0a(a2b >=
Під-
ставляючи координати точки A(1;2) і
a2b = у рівняння (2.56), оде-
ржимо
1
a
2
2
a
1
=+
, або
1
a
2
=
і .2a =
Тоді рівняння шуканої прямої буде
1
4
y
2
x
=+
.
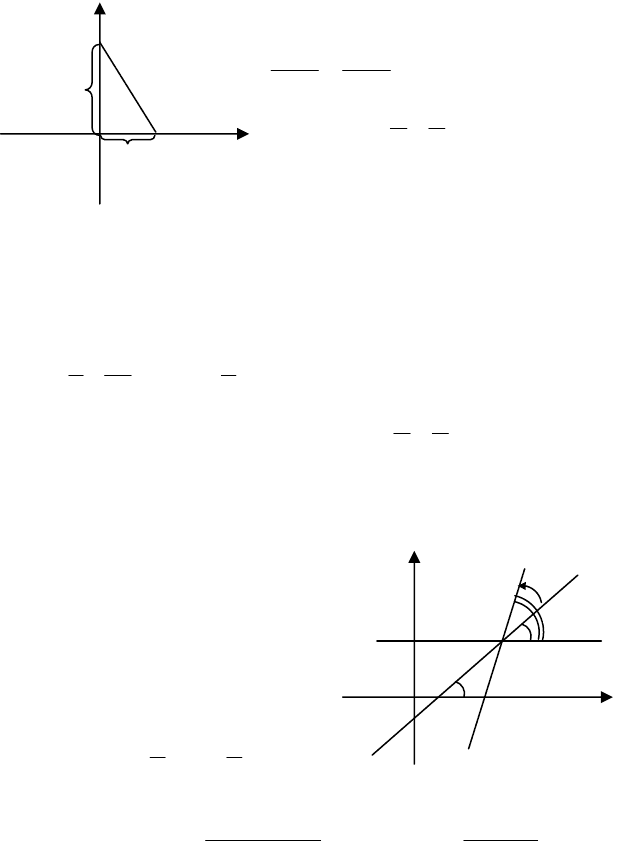
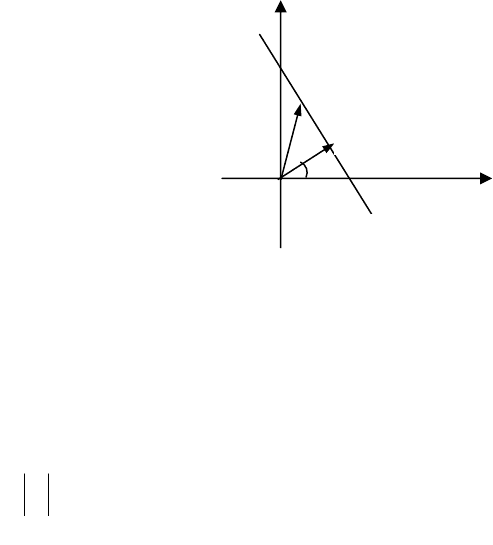
16.5. Кут між двома прямими
Нехай задано дві прямі
1
l
і
2
l
:
11
bxky +=
,
1
l
22
bxky += ,
2
l
і потрібно знайти кут
ϕ
між ними
(мал.40).
Із мал.40 видно, що
12
ϕ
−
ϕ
=
ϕ
, причому
11
tgk
ϕ
=
,
22
tgk
ϕ
= ,
2
1
π
≠ϕ
,
2
2
π
≠ϕ
.
Тоді
21
12
12
tgtg1
tgtg
)(tgtg
ϕϕ+
ϕ
−
ϕ
=ϕ−ϕ=ϕ
або
21
12
kk1
kk
tg
+
−
=ϕ
(2.57)
де стрілка на мал. 40 означає, що кут
ϕ
береться проти годиннико-
вої стрілки від
1
l до
2
l .
A(a,0)
B(0,b)
Мал.39
х
у
О
a
b
φ
1
l
1
у
Мал.40
67
х
φ
1
φ
φ
2
l
2
133
Формула (2.57) є формула для знаходження кута між двома
прямими.
Якщо
l
1
⎪⎪l
2
то 0=
ϕ
і 0tg =
ϕ
. Тоді із формули (2.57) маємо,
що
21
kk =
(2.58)
Умова (2.58) є необхідною і достатньою умовою паралельнос-
ті двох прямих.
Якщо
,ll
21
⊥ то тоді
2
π
=ϕ
і
ϕ
tg
не існує. Перейдемо до
.
tg
1
ctg
ϕ
=ϕ
Тепер формула (2.57) запишеться так
12
21
kk
kk1
tg
1
ctg
−
+
=
ϕ
=ϕ
і коли
2
π
=ϕ
, то 0)
2
(ctg =
π
. Одержимо
умову перпендикулярності двох прямих:
1kk
21
−= (2.59)
Висновок
. Прямі
1
l і
2
l паралельні тоді і тільки тоді, коли їх
кутові коефіцієнти рівні і ці прямі перпендикулярні, коли добуток їх
кутових коефіцієнтів дорівнює “–1”.
Приклад 3. Знайти кут між прямими
4x3y += і
.1x
2
1
y −=
Розв
’язування. Знаходимо
2
1
k
1
= і 3k
2
= . Підставивши зна-
чення цих кутових коефіцієнтів у формулу (2.57), одержимо
.1
3
2
1
1
2
1
3
tg =
⋅+
−
=ϕ
Звідси знаходимо
45=ϕ .
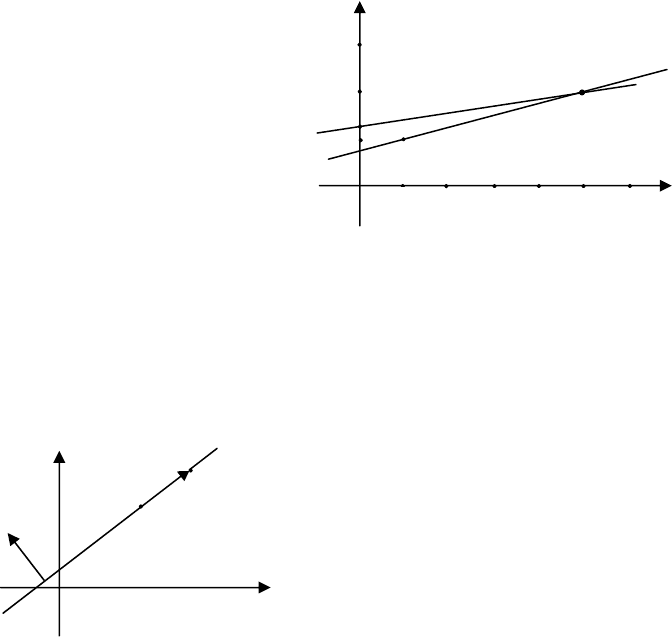
Приклад 4. Затрати перевезень двома засобами транспорту
виражаються функціями
x2575y +=
і
x15125y +=
, де
x
- від-
даль перевезень в сотнях кілометрів, а
y
- транспортні витрати. По-
чинаючи з якої віддалі , найбільш економічним є другий засіб тран-
спорту?
134
Розв’язування. Намалюємо графіки заданих функцій і побачи-
мо, що вони перетинаються в
точці (5;200). Щоб перевірити
даний результат, розв’яжемо
систему рівнянь
⎩
⎨
⎧
+=
+=
x15125y
x2575y
,
x15125x2575 +=+
або
,50x10 = 5x = ,
.200y =
З даного малюнка видно,
що при віддалі, яка перевищує
500 км найбільш економічним є дру-
гий засіб транспорту.
16.6. Загальне рівняння прямої та його дослідження.
Нехай задана точка
)y;x(М
)000
через яку проходить пряма l
і вектор
)B,A(n
→
, який перепендикулярний до прямої l (мал.41). На
прямій
l беремо довільну точку
)y;x(M
. Тому що вектор
→
MM
0
є
перепендикулярним до вектора
)B,A(n
→
, то скалярний добуток цих
векторів дорівнює нулю, тобто
0nMM
0
=⋅
→→
. (2.60)
Рівняння (2.60) є векторне рівняння прямої
l
. Розпишемо це
рівняння в координатній формі. Оскільки
),yy;xx(MM
000
−−=
→
то
рівняння (2.60) перепишеться у вигляді
.0)yy(B)xx(A
00
=−+−
Розкривши дужки, одержимо
0CByAx =++ , (2.61)
де
00
ByAxС −−= .
Рівняння (2.61) називається загальним рівнянням прямої. Дос-
лідимо як розміщена пряма, що задана рівнянням (2.61), якщо деякі
коефіцієнти
B,A і С будуть рівні нулю.
B)(A,n
→
Мал.41
М(х
0
,у
0
)
у
О
х
М(х,у)
l
І
ІІ
100
200
300
О
у
х
1
2
3
4
5
6

135
1) Якщо 0B,0A,0С ≠≠= , то рівняння (2.61) має вигляд
0ByAx =+
або
kxx
B
A
y =−=
, де
.
B
A
k −=
Значить, якщо вільний член , а саме
0С = , то пряма прохо-
дить через початок координат.
2) Якщо
0С,0B,0A ≠≠= , то рівняння прийме вигляд
0СBy =+ або b
B
C
y =−=
, тобто пряма паралельна осі .Ox
3) Якщо
0C,0A,0B ≠≠= , то рівняння (2.61) має вигляд
0CAx =+ або a
A
C
x =−=
є рівнянням прямої, паралельної осі ор-
динат.
4) Якщо
0С,0B,0A =≠=
, то рівняння прийме вигляд
0By = , звідси .0y = Це і є рівняння осі .Ox
5) Якщо
0С,0B,0A ==≠
, то рівняння (2.61) буде мати ви-
гляд
0Ax = або 0x = . Це рівняння осі
.Oy
Якщо задані дві прямі
1
l і
2
l загальними рівняннями
0CyBxA
111
=++
,
1
l
,
0CyBxA
222
=++ ,
2
l .
то щоб знайти координати точки перетину цих прямих, які повинні
задовольняти рівняння кожної прямої, то потрібно розв’язати сис-
тему рівнянь
⎩
⎨
⎧
=++
=++
.0CyBxA
,0CyBxA
222
111
Якщо прямі
1
l і
2
l паралельні, то їх кутові коефіцієнти
2
1
1
B
A
k −=
і
2
2
2
B
A
k −=
рівні. Отже,
21
kk = або
2
1
2
1
B
B
A
A
=
.
Значить, умова паралельності прямих, які задані загальними
рівняннями, є пропорціональність коефіцієнтів при невідомих.
Умова перпендикулярності прямих
1kk
21
−= в цьому випадку
має вигляд
1)
B
A
)(
B
A
(
2
2
1
1
−=−−
або 0ВВАА
2121
=+ .
136
Отже, для прямих
,ll
21
⊥
які задані загальними рівняннями,
умовою перпендикулярності є рівність нулю суми добутків коефіці-
єнтів при змінних
x
і
y
.
16.7. Нормальне рівняння прямої
Нехай положення прямої на площині визначається двома
величинами (параметрами прямої) : довжиною і напрямком
перпендикуляра
ОР, опущеного із початку координат на пряму і ве-
личиною кута
α
, який утворює даний перпендикуляр з віссю
Ox
(мал.42).
На прямій
l візьмемо довільну точку
)y,x(M
. Позначимо
довжину перпендикуляра через
p
, а
орт нормалі через
→
n . Проекція раді-
ус-вектора
→→
= OMr на нормаль буде
завжди рівною
p
.
Таким чином, пряма
l визна-
чається як геометричне місце точок
площини, проекції радіус-векторів
яких на нормаль дорівнює сталій ве-
личині
p
.
На основі скалярного добутку маємо
,nrrПр
n
→
→→
⋅=
→
pnr =⋅
→
→
. (2.62)
Рівняння (2.62) є нормальним рівнянням прямої у векторній
формі.
Тому що
1n =
→
, координати
)sin,(cosn αα=
→
, вектор
),y,x(OM =
→
то в координатній формі рівняння (2.62) буде мати ви-
гляд
0psinycosx =−α+α . (2.63)
Якщо пряма лінія задана загальним рівнянням
,0CByAx =++
α
у
М(х,у)
О
х
l
P
Мал.42

137
то це рівняння можна звести до нормального рівняння прямої
(2.63).Помножимо загальне рівняння прямої на деякий множник
μ
,0CByAx =
μ
+
μ
+
μ
(2.64)
Одержане рівняння і загальне рівняння прямої рівносильні.
Щоб рівняння (2.64) було нормальним, тобто мало вигляд (2.63) по-
трібно, щоб виконувалися рівності
⎪
⎩
⎪
⎨
⎧
−=μ
α=μ
α=μ
.pC
,sinB
,cosA
(2.65)
Перші дві рівності в (2.65) піднесемо до квадрату і додамо.
Тоді одержимо, що
22
BA
1
+±
=μ
, (2.66)
μ
називається нормувальним множником.
Третя рівність (2.65) встановлює знак множника
μ
, а саме
знак
μ
є протилежним знакові вільного члена .C
Приклад 4. Привести до нормального вигляду рівняння
.07y3x4 =−−
Розв
’язування. Знаходимо нормувальний множник
.
5
1
)3(4
1
22
=
−++
=μ
(вибираємо знак плюс, так як
).07C <−=
Помноживши на
5
1
дане рівняння, одержимо
.0
5
7
y
5
3
x
5
4
=−−
Одержане рівняння і є нормальним рівнянням прямої. В цьому
рівнянні
,
5
4
cos =α
,
5
3
sin −=α
5
7
p =
.
16.8. Віддаль від точки до прямої
Нехай маємо пряму
l, задану рівнянням
0psinycosx =−α+α
і точку
М
0
(х
0
,у
0
) Потрібно знайти віддаль від цієї точки до прямої l.
Через точку
)y;x(M
000
проведемо пряму
1
l паралельну прямій l
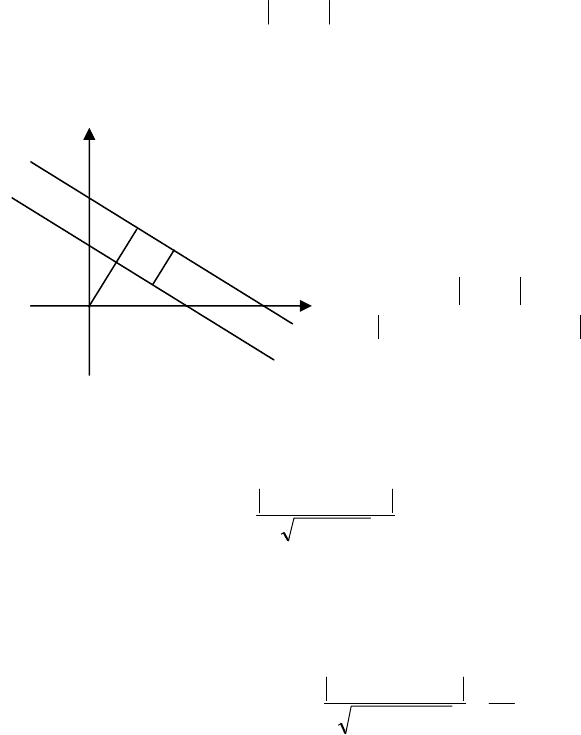
138
Шукану віддаль від точки
М
до прямої l позначимо через
.DMd
о
=
Тому що
,pOP =
а
11
pOP =
, то
.ppd
1
−=
Якщо б точка
0
М знаходилася на тій же віддалі від прямої l ,
але з другого боку, то тоді
).pp(d
1
−−=
Таким чином, шукана віддаль визначається рівністю
()
ррd
1
−±=
або ppd
1
−= .
Нормальне рівняння прямої
1
l паралельної l має вигляд
0psinycosx
1
=−α+α . (2.67)
Тому що точка
)y;x(M
000
знаходиться на прямій
1
l
, то її
координати задовольняють рів-
нянню (2.67), тобто
0psinycosx
100
=−α+α
і звідси
α+α= sinycosxp
001
.
Підставляючи значення
1
p в
рівність
ppd
1
−= , одержимо
рsinycosxd
00
−α+α= (2.68)
Формула (2.68) є форму-
лою віддалі від точки
)y;x(M
000
до прямої, заданої нормальним рівнянням.
Якщо ж пряма задана загальним рівнянням, то віддаль від то-
чки
)y;x(M
000
знаходиться за формулою
22
00
BA
CByAx
d
+
++
=
. (2.69)
Приклад. Знайти віддаль від точки
)4;3(М
0
до прямої
.010y3x4 =+−
Розв
’язування. Тепер підставляємо замість
0
x і
0
y координа-
ти точки
0
M , тобто ,3x
0
= 4y
0
= в формулу (2.69) і знаходимо
шукану віддаль
.2
5
10
)3(4
104334
d
22
==
−+
+⋅−⋅
=
§17. Площина та її рівняння
Нехай в системі координат xyz0 задана довільна площина π .
l
1
P
1
М
0
(х
0
,у
0
)
D
p
у
О
х
l
P
Мал.43
139
Візьмемо на цій площині яку-небудь точку
).z,y,x(M
0000
Виберемо вектор
)C,B,A(n
→
перпендикулярний до площини
π
і
назвемо його нормальним
вектором, або просто нормаллю.
Цими
двома величинами (точкою
через яку проходить площина і
вектором
перпендикулярним до
площини)
площина визначаєть-
ся однозначно. На площині
π
візьмемо довільну точку
)z,y,x(M (мал.44). Тому що
точка
)z,y,x(М знаходиться
на площині, то вектор
→
MM
0
перпендикулярний до
вектора
→
n , а це значить, що їх скалярний добуток дорівнює нулю,
тобто
0nMМ
0
=⋅
→→
(2.70).
Рівняння (2.70) є векторним рівнянням площини. Розпишемо
рівняння (2.70) в координатній формі , знаючи, що
)zz;yy;xx(MM).C,B,A(n
0000
−−−=
→→
. Одержимо
0)zz(C)yy(B)xx(A
00)0
=−+−+− (2.71).
Рівняння (2.71) є рівнянням площини, що проходить через за-
дану точку
)z,yx(M
00,00
і перпендикулярна до заданого вектора
)C,B,A(n
→
. Рівняння (2.71) задовольняють координати довільної
точки, яка знаходиться на цій площині
π і не задовольняють коор-
динати довільної точки, яка не знаходиться на цій площині.
Розкривши дужки в рівнянні (2.71), одержимо
,0DСzByAx =+++
(2.72)
де
000
CzByAxD −−−= . Рівняння (2.72) називається загальним рів-
нянням площини. Кожна площина в декартових прямокутних коор-
динатах визначається рівнянням першого степеня відносно біжучих
координат
.
z
.
y
,
x
Вірно і обернене твердження: кожне рівняння
першого степеня відносно біжучих координат
z
,
y
,
x
визначає
х
π
O
M
z
у
M
0
→
n
Мал.44
140
площину.
Дійсно, нехай
000
z,y,x - який –небудь розв’язок рівняння
(2.72), тобто
0DCzByAx
000
=+++ . (2.73).
Віднімаючи почленно із рівняння (2.72) рівність (2.73), одер-
жимо рівняння
,0)zz(C)yy(B)xx(A
000
=−+−+− яке і є рівнян-
ням площини, що проходить через точку
)z,y,x(M
0000
і перпенди-
кулярна до вектора
)C,B,A(n
→
.
17.1. Дослідження загального рівняння площини
Під дослідженням загального рівняння площини розуміється
те, яке положення займає площина, коли деякі із коефіцієнтів
C,B,A і
D
перетворюються в нуль.
1)
0C,0B,0A,0D ≠≠≠= , то рівняння площини має
вигляд
,0CzByAx =++ тобто площина проходить через початок
координат;
2)
,0D,0B,0A,0C ≠≠≠= то рівняння (2.72) буде
мати вигляд
0DByAx =++ .
В площині
xy0
це рівняння визначає пряму лінію, а в просто-
рі це буде рівняння площини паралельної вісі
.z0
3)
0D,0C,0A,0B ≠≠≠= , то рівняння (2.72) буде мати
вигляд
0DCzAx =++ .
і є рівнянням площини, паралельної вісі
.Оy
4)
,0D,0C,0B,0A ≠≠≠= то рівняння (2.72) має ви-
гляд
0DCzBy =++ і є рівнянням площини , яка паралельна вісі
x0 . Отже, якщо в рівнянні площини (2.72) відсутня одна із коорди-
нат
y
,
x
або
z
то площина паралельна вісі y0,x0 або z0 .
5) Якщо
0CD ==
, ,0B,0A ≠≠ то рівнянню 0ByAx =+
відповідає площина, яка проходить через початок координат і пара-
лельна вісі z0 , тобто ця площина проходить через вісь z0 ;
