Шинкарик М.І. Вища математика

Подождите немного. Документ загружается.

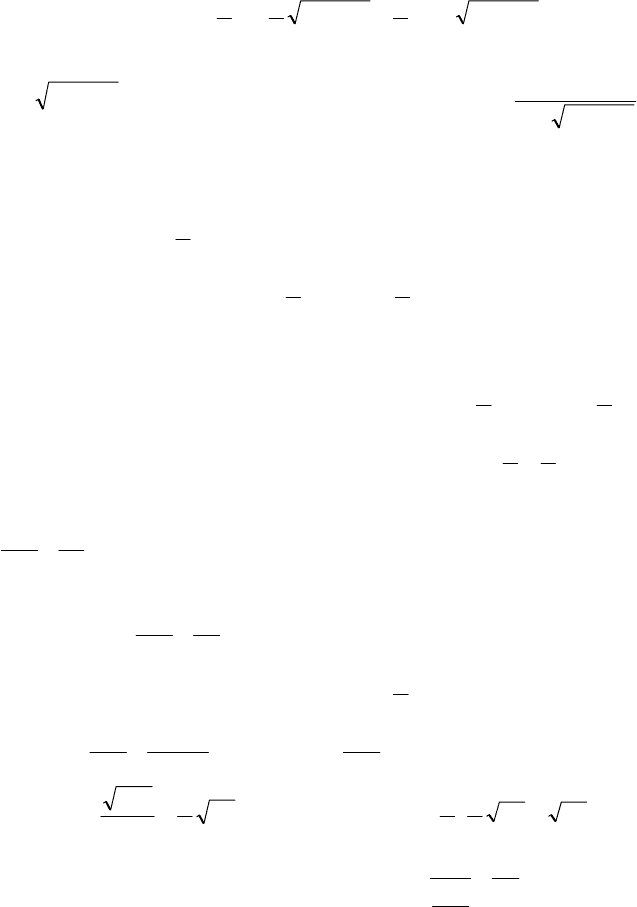
161

)axx(

2222

−−=−−=− .

Тепер помножимо і розділимо праву частину цієї рівності на

axx ++ і після спрощень одержимо

axx

−+

=−

Звідси видно, що при необмеженому збільшенні абсциси

x різниця

Y-y

необмежено зменшується . Таким чином, точка гіперболи необ-

межено віддаляючись по вітці гіперболи, необмежено наближається

до асимптоти x

Y = , але ніколи її не досягає. Значить, гіпербола

(2.135) має дві асимптоти

Y =

Y −=

, які співпадають з діа-

гоналями прямокутника і проходять через початок координат.

Приклад 4. Скласти рівняння гіперболи, якщо відомо, що вона

проходить через точку M

(10;5) і має асимптоти x

y = та x

y −= .

Розв

’язування. З умови задачі одержуємо, що

та коор-

динати точки

задовольняють рівнянню гіперболи, тобто

=−

Таким чином, одержали систему двох рівнянь з двома

невідомими:

⎪

⎩

⎪

⎨

⎧

=−

100

,b5a4

З першого рівняння знаходимо

b = і підставляємо в друге

рівняння

a16

2525

100

⋅

−

або

975

Звідси

975

a == . Далі знаходимо .3939

b =⋅=

Отже, шукане рівняння гіперболи буде

975

=−

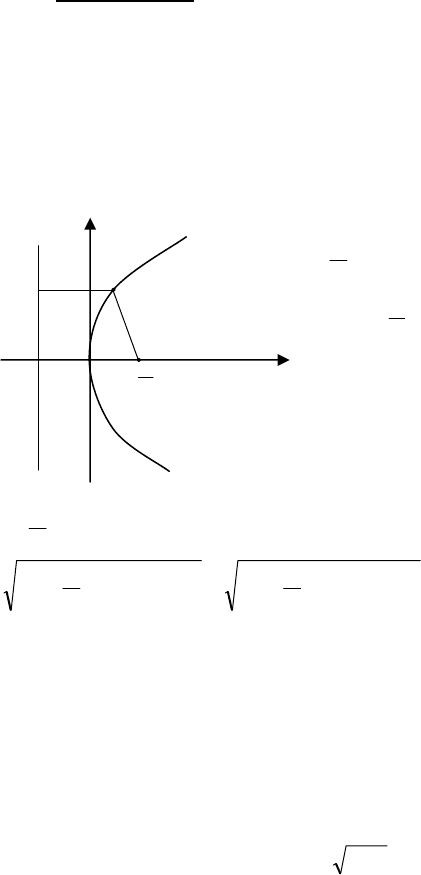
162

19.5. Парабола та її рівняння

Означення 7. Параболою називається множина точок

площини, однаково віддалених від заданої точки, що називається

фокусом і від заданої прямої, що називається директрисою.

Виходячи з означення 7, виведемо рівняння параболи. Нехай

пряма

AB є директрисою параболи, а точка F є її фокусом (мал.61).

Проведемо через точку

пряму перпендикулярну до директриси

AB і візьмемо цю пряму за вісь абсцис, а за вісь ординат вієьмемо

пряму перпендикулярну до вісі абсцис і яка проходить через точку

O, середину відрізка CF. Довжину відрізка CF позначимо через p

(p>0)

. Координати фокуса будуть

)0,

(

, а рівняння директриси AB

x −=

Нехай точка M(x,y) є

довільною точкою параболи. Опу-

стимо із точки

M перпендикуляр

на директрису

AB в точці D і спо-

лучимо точку

M з фокусом F. Тоді

за означенням 7 маємо, що

DM=MF Точка D має координати

).y,

(−

За формулою віддалі між двома точками знаходимо

2222

)0y()

x()yy()

x( −+−=−++ .

Це і буде рівняння параболи відносно вибраної системи коор-

динат. Підносячи обидві частини даного рівняння до квадрату, і

спростивши, одержимо

px2y

= . (2.142)

Рівняння (2.142) і є канонічним рівнянням параболи. Як видно

з рівняння (2.142) парабола є лінія другого порядку і всі її точки ро-

зташовані праворуч від осі

. Парабола проходить через початок

координат. Розв’язавши рівняння (2.142) відносно

одержимо

px2y ±=

. (2.143)

Так як

0p >

, то

буде дійсною величиною тільки тоді, коли

додатні, а коли ,0p < то парабола визначена для

0x ≤

,0)

Мал.61

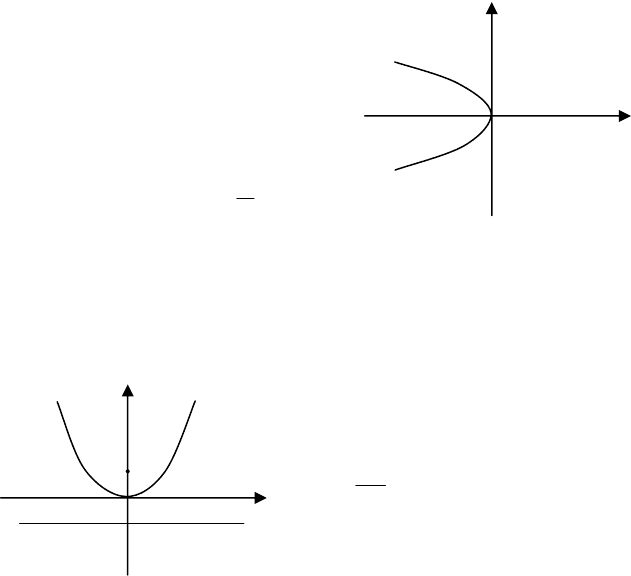
163

Із (2.143) видно, що кожному значенню

відповідає два зна-

чення

, які рівні за абсолютною величиною, але протилежні за

знаком.

Значить вісь

x0 є віссю симетрії для параболи.

Точку

)0,0(O називають вершиною параболи.

Якщо

x необмежено зростає, то і y необмежено зростає. Вели-

чина

р називається параметром параболи і при збільшенні р парабо-

ла розширюється, тобто її точки будуть віддалятися від осі

Ох.

Якщо рівняння параболи має

вигляд

=−2px то вершина параболи

знаходиться в початку координат,

вісь симетрії є вісь абсцис, але пара-

бола розміщена зліва від осі

(мал.62), а директриса такої парабо-

ли буде розміщена праворуч від осі

ординат, а фокус

)0,

(F −

буде

ліворуч від початку координат.

Якщо директриса параболи паралельна вісі абсцис , а фокус

знаходиться на вісі ординат, то рівняння параболи має вигляд

=±2py. (2.144)

Парабола (2.144) зображена на мал.63. Це парабола

симетрична відносно осі

Oy і розміщена над віссю абсцис, якщо в

рівнянні взяти знак (+) і під віссю аб-

сцис, якщо взяти знак (-).

Якщо в рівнянні (2.144) позна-

чити

=±

, то одержимо рівняння

параболи

axy =

, яку вивчають в

середній школі.

Приклад 5. Ферми, які підтримують залізнодорожний міст

довжиною 112 м, мають вигляд параболи, яка задається рівнянням

.axy

Знайти рівняння відповідної параболи, якщо найбільша

висота мостової арки складає 44м.

Розв

’язування. Візьмемо за початок координат вершину фер-

ми. Тоді симетричні точки в основі ферми будуть мати координати

(-56,-44) і (56,-44). Підставляючи будь-яку пару координат в рівнян-

px2

y −=

Мал.62

Мал.63

164

ня

axy = , одержимо 3136a44 ⋅=− . Звідси

787

3136

a −=−=

Таким чином, мостова ферма має вигляд параболи

784

y −=

§20. Перетворення прямокутних координат

Виводячи рівняння еліпса,

гіперболи та параболи, ми певним

чином вибирали систему коорди-

нат для кожної із цих ліній. Вини-

кає питання, як впливає на форму

рівняння інше розміщення коор-

динатних осей? При переході від

однієї системи координат до дру-

гої системи координат змінюються

як координати точок так

і рівняння

кривих .

Тепер розглянемо перехід від однієї прямокутної системи ко-

ординат до такої ж шляхом паралельного зсуву осей, коли зміню-

ється початок координат, а напрям осей залишається той же.

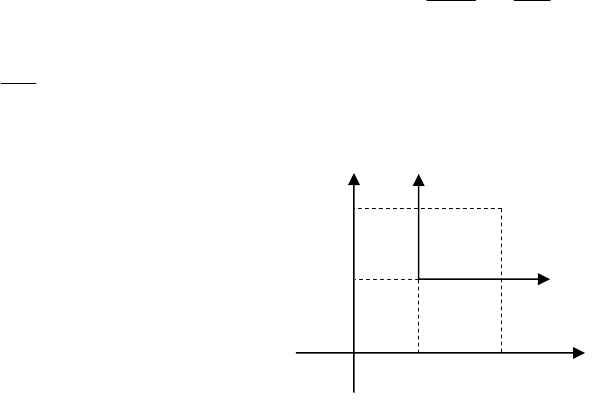
20.1. Перенесення початку координат

Нехай точка

M площини має координати (x,y) в прямокутній

системі координат

Oxy. Перенесемо початок координат в точку

),b,a(0

де

і b є координатами точки

в старій системі коор-

динат

.xy0 Осі

x0 та

y0 нової системи координат залишаються

паралельними осям

x0 і

старої системи координат ( не зміню-

ється напрям осей( мал.64).

Позначимо координати точки

в новій системі координат

через

).y;x(

Виведемо формули, які показують зв’язок між ста-

рими і новими координатами точки

.M Для цього опустимо перпе-

ндикуляри

MM на вісь

MM на вісь y0 , а також перпенди-

куляри

на

на вісь

. Для відрізків

M0,A0

справедлива рівність

M0AMA0 =+ . Оскільки OA=a, OM

=x,

Мал.64

(а,в)

165

, то x=a+x

. Аналогічно, знайдемо рівність

yby +=

Формули

⎭

⎬

⎫

yby

xax

(2.145)

і вказують на зв’язок між старими і новими координатами точки при

паралельному перенесенні початку координат.

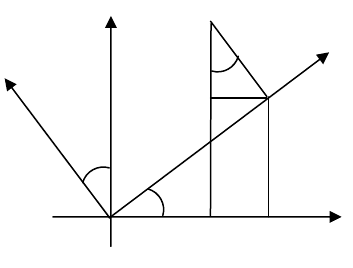
20.2. Поворот осей координат

Розглянемо тепер випадок, коли нова система координат

111

yx0

одержується із старої

системи координат шляхом

повороту її навколо початку

координат

0 на кут α

(мал.65).

Нехай координати

довільної точки

в старій

системі координат

xy0 є

)y,x( , а в новій системі ко-

ординат

yx0

).y,x(

Відлік кута

α повороту про-

водиться в напрямі, протилежному рухові годинникової стрілки.

Із малюнка 65 видно, що

=x, MM

=y, OM

, MM

Для відрізків

,AM,M0,A0

а також для відрізків

MB,BM,MM

справедливі рівності

⎩

⎨

⎧

+=+=

−=−=

.BMAMBMBMMM

,BMA0AMA0M0

211

(2.146)

Із прямокутних трикутників

AM0

BMM одержуємо

.sinysinMMBM

,cosycosMMBM

,sinxsinM0AM

,cosxcosM0A0

122

α=α=

Підставимо знайдені значення

BM,BM,AM,A0 в рівності

(2.146), і одержимо формули переходу від старих координат до но-

вих при повороті осей на кут

Мал.65

166

⎩

⎨

⎧

α+α=

α−α=

.cosysinxy

,sinycosxx

(2.147)

Тепер, щоб виразити нові координати

точки М через

старі координати

можна із системи (2.147) двох рівнянь з дво-

ма невідомими знайти

та

Оскільки, формули для нових координат можна одержати по

другому: так як нова система координат одержалася із старої систе-

ми поворотом на кут

α , то стара система одержиться поворотом

осей на кут (-

α ). Значить в рівняннях (2.147) можна поміняти міс-

цями старі і нові координати, замінивши однозначно

α на (-α ), то

одержимо

⎩

⎨

⎧

α+α−=

α+α=

.cosysinxy

,sinycosxx

(2.148)

Приклад 1. Який вигляд буде мати крива

,07y4yx2x

=−−−+ якщо за нові осі координат взяти прямі,

які проходять через точку

)2,1(0

−− і паралельні старим осям ко-

ординат.

Розв

’язування. За формулами (2.145) маємо , що

⎩

⎨

⎧

−=

2yy

1xx

Підставивши

та

в рівняння кривої, одержимо

.07)2y(4)2y()1x(2)1x(

=−−−−−−+− Після спрощення

одержимо

4yx

=−

або

=−

Нове рівняння лінії є рівностороння гіпербола.

Приклад 2. Який вигляд прийме рівняння гіперболи

4yx

=− , якщо осі координат повернути на кут ( )45

− ?

Розв

’язування. Оскільки гіпербола 4yx

=− є рівносторон-

ньою, то

= і

−= є асимптотами цієї гіперболи. Приймемо

асимптоти гіперболи за нові осі координат, оскільки вони взаємопе-

рпендикулярні, бо добуток їх кутових коефіцієнтів дорівнює (-1).

Замінимо

та

за формулами (2.147) , де

45−=α , маємо

167

).xy(

)45cos(y)45sin(xy

),yx(

)45sin(y)45cos(xx

−=−+−=

+=−−−=

Заміняючи

та

в рівнянні гіперболи, одержимо

4)xy(

)yx(

=−−+ , або після спрощень маємо

;2yx

= тобто

Це є гіпербола, яку вивчають у шкільному курсі математики, і

яка задає обернено пропорційну залежність.

§21. Полярна система координат

Найбільш важливою після пря-

мокутної системи координат є полярна

система координат. До цього положен-

ня точки на площині ми визначали

двома числами (координатами) в пря-

мокутній системі координат, але це

можна

однозначно визначити за допомогою полярної системи коор-

динат. Вона складається із деякої точки

0, яка називається полюсом

і променя

, який виходить із цієї точки, який називається поляр-

ною віссю (мал. 66). Крім цього задається одиниця масштабу.

Нехай точка

М довільна точка площини, а

віддаль цієї точ-

ки від точки

0, а

це кут, на який потрібно повернути полярну вісь

для суміщення з променем

M0 .

Полярними координатами точки

називаються числа

. Число

вважається першою координатою і називається поляр-

ним радіусом, а число

- другою координатою і називається поля-

рним кутом. Точка

з полярними координатами позначається так

).,(M

Полярний радіус може змінюватися в межах:

+∞<

≤0 , а

полярний кут в межах:

;20 π<

≤

при цьому відлік полярного кута

проводиться від полярної осі проти годинникової стрілки.

Мал.66

168

Між координатами точки у полярній системі координат та її

координати в декартовій системі існує простий зв’язок.

Візьмемо вісь

x0 декартової системи координат за полярну

вісї полярної системи, а початок декартової системи приймемо за

полюс полярної системи координат.

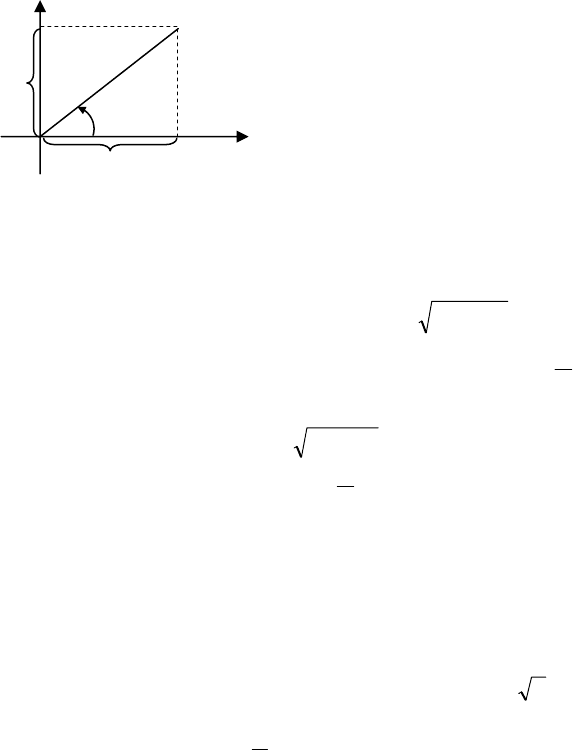
Нехай точка

має прямокутні коор-

динати

x та y і полярні координати

та

(мал.67). Як видно з мал.67, має-

мо

⎩

⎨

⎧

ϕρ=

.siny

,cosx

(2.149)

Формули (2.149) виражають прямокутні координати через по-

лярні.

Якщо піднести до квадрату обидві частини рівностей (2.149) і

додати, то одержимо ,yx

222

ρ=+ або .yx

+=ρ Якщо ж поді-

лити другу рівність на першу в (2.149), то дістанемо

tg =ϕ

Формули

⎪

⎭

⎪

⎬

⎫

=ϕ

+=ρ

(2.150)

визначають полярні координати через декартові. При визначенні

полярного кута слід враховувати знаки

та

користуючись фор-

мулами (2.149).

Приклад 1. Дано прямокутні координати точки (1;1). Знайти

її полярні координати, вважаючи, що полюс суміщений з початком

додатної півосі абсцис.

Розв

’язування. За формулами (2.150) маємо

.1tg,2 =ϕ=ρ

Згідно другої рівності

=ϕ

, так 01xsin >= і .01y >=

Розглянемо деякі криві в полярній системі координат.

1) Спіраль Архімеда.

Ця крива визначається рівнянням

Мал.67

169

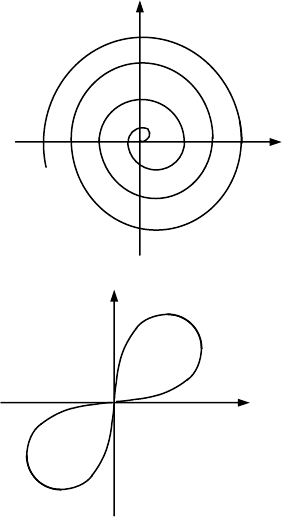
Вигляд спіралі Архімеда має

пружина в годиннику(мал.68).

2) Лемніската Бернуллі.

Рівняння цієї кривої в полярній

системі координат є

.2sinar

ϕ=

Графік цієї кри-

вої зображений на мал. 69.

Мал.68

Мал.69

170

Розділ 3. ВСТУП У МАТЕМАТИЧНИЙ АНАЛІЗ

§ 1. Множини дійсних чисел

1.1. Сталі і змінні величини

Коли ми вивчаємо деякі питання з області математики, фізики,

механіки, економіки і т.д., то зустрічаємося з величинами, які збері-

гають стале числове значення і називаються сталими, а інші можуть

приймати різні числові значення і називаються змінними.

Наприклад, до сталих величин можна віднести число

π , яке

рівне відношенню довжини кола до діаметра.

До змінних величин можна віднести температуру зовнішнього

середовища, яка протягом дня змінюється; загальну суму грошей,

яку отримує магазин від продажу продукції протягом дня і т.д.

1.2. Множини дійсних чисел

У курсі вищої математики найбільший інтерес становлять чи-

слові множини, тобто множини, елементами (

величинами) яких є

числа. Серед числових множин будемо розглядати такі:

1) Множина всіх натуральних чисел

}{

;,...n,...,3,2,1N =

2) Множина всіх цілих чисел

{}

;,...n,...,2,1,0Z ±±±=

3) Множина всіх раціональних чисел

⎭

⎬

⎫

⎩

⎨

⎧

−

ціле, −

на-

туральне число.

4) Множина всіх дійсних чисел

Множина всіх дійсних чисел складається з усіх раціональних і

ірраціональних чисел. Ірраціональними числами називаються не-

скінченні неперіодичні десяткові дроби. Наприклад,

, ,3lg



20sin і т.д.

Зауважимо, що пряма лінія, на якій вказані початок відліку,

масштаб і напрямок, називається числовою віссю.

Між множиною точок числової осі і множиною всіх дій-

сних чисел існує взаємно однозначна відповідність. Це озна-

чає, що кожна точка числової осі відображає одне дійсне чис-

ло, і навпаки, кожне число являється координатою конкретної

однієї точки числової осі.