Шинкарик М.І. Вища математика
Подождите немного. Документ загружается.

191
3)
5
76
27
7
n
1
1
n
1
n
1
1
nn
1nn
+
++
=
+
++
.
Далі, використовуючи основні теореми про границі, і здійс-
нюючи граничний перехід при
∞→
n
, одержуємо такі
відповіді: 1)
;0
1
0
;
01
00
n
1
1
n
1
n
1
lim
nn
3n
lim
2
3
n
3
2
n
==
+
−
=
+
−
=
+
−
∞→∞→
2)
;
n
1
n
1
n
1
n
1
1
lim
nn
nnn
lim
43
4
n
2
45
n
∞=
+
++
=
+
++
∞→∞→
3)
.1
01
001
n
1
1
n
1
n
1
1
lim
nn
1nn
lim
5
76
n
27
7
n
=
+
++
=
+
++
=
+
++
∞→∞→
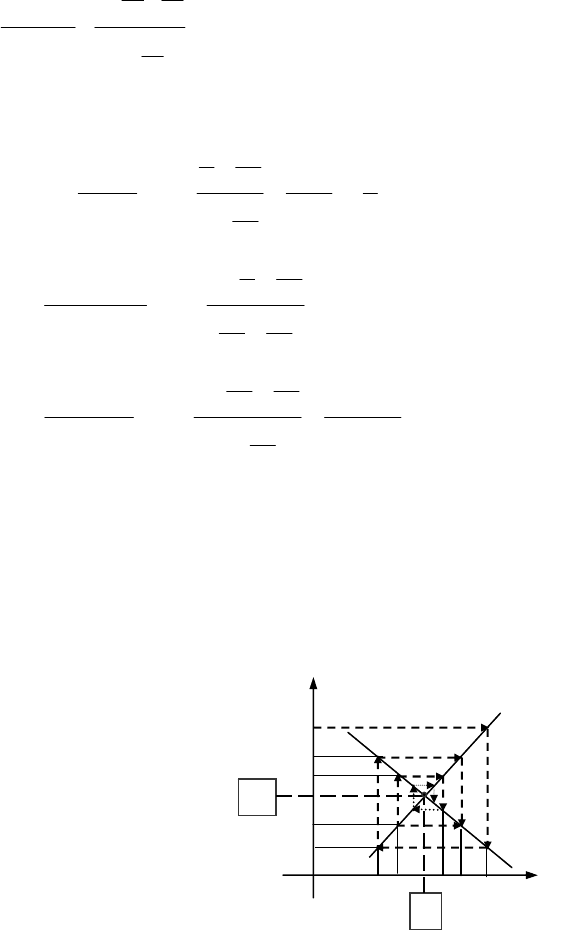
3.5. Павутинна модель ринку
Розглянемо найпростішу модель ринку одного товару і
процес пошуку (“нащупування”) рівноважної ціни. Це є одна з
основних проблем ринку, яка означає фактично торг між виро-
бником (продавцем) і покупцем.
Ми уже розглядали функції попиту і пропозиції від ціни на
товар, а також їх графіки. Зрозуміло, що
в загальному випадку ці
залежності нелінійні. Для
спрощення ситуації, графіки
цих функцій можна замінити
прямими (графіками дотичних
до цих кривих в заданих точ-
ках). Нехай спочатку виробник
(продавець) визначає ціну
1
P
на
товар. Зрозуміло, що ця ціна
1
P
є вищою за рівноважну (кож-
ний виробник хоче мати найбі-
S
1
Q
3
Q
2
Q
1
P
3
P
4
P
5
P
2
P
1
S
Q
P
0
S
0
S,Q
Р
192
льший прибуток від виробництва товарів). Покупець оцінює попит
1
Q при цій ціні і визначає свою ціну
2
P , при якій цей попит
1
Q рів-
ний пропозиції
1
S
. Ціна
2
P
нижча рівноважної (кожний покупець
хоче купити дешевше товар). В свою чергу продавець оцінює попит
2
Q
, що відповідає ціні
2
P
, і визначає свою ціну
3
P
і т.д. Процес
торгу продовжується і в кінцевому випадку приведе до рівноважної
ціни
0
P
( павутина закручується). Якщо розглянути послідовність
чисел
,...,p,p,p
321
то ця послідовність має границю .PlimP
n
n
0
∞→
=
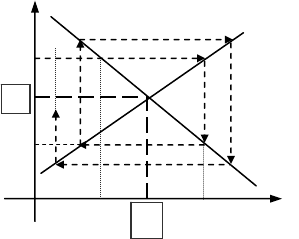
Ми розглянули збіжну модель. Зрозуміло, що може бути і ро-
збіжна модель, тобто рівноважну ціну
знайти не можливо.
Розглянемо малюнок.
В даній ситуації, нехай вироб-
ник (продавець) визначає ціну
1
Р на
товар. Очевидно, що ця ціна є вищою
за рівноважну. Покупець оцінює по-
пит
1
Q
при цій ціні і визначає свою
ціну
2
Р , при якій цей попит
1
Q рів-
ний пропозиції
1
S
. Ціна
2
Р
нижче рівноважної і т.д.
Процес торгу продовжується і павутина розкручується. Якщо
розглянути послідовність чисел
,...,p,p,p
321
то ця послідовність
розбігається:
∞=
∞→
n
n
plim
.
3.6. Існування границі монотонної числової послідовності
ТЕОРЕМА. Якщо послідовність
,...x,...,x,x
n21
є монотонно
зростаючою (спадною) і обмежена зверху (знизу), то вона збіжна.
Доведення
. Нехай послідовність
)x(
n
є спадною, тобто
...x...,xx
n21
>>>> , і нехай вона обмежена знизу, тобто існує таке
число
m
, що ,mx
n
≥
,...2,1n =
Тоді множина значень послідовності
(x
n
) має нижню грань,
яку позначимо через
).xinf(a
n
= Покажемо, що
.axlim
n
n
=
∞→
Оскі-
льки
а є нижня грань множини значень послідовності (x
n
), то для
всіх її значень виконується нерівність
x
n
>a.
S
2
S
1
Q
2
Q
1
P
2
P
1
Q
P
0
S
0
S,Q
Р

193
Проте, згідно з властивістю нижньої грані, яке б ми не взяли
як завгодно мале додатне число ε
>0 знайдеться таке натуральне чи-
сло
N
, що ε+< ax
N
. Тоді, беручи до уваги те, що послідовність
спадна, дістаємо нерівність
ε+<< axa
n
як тільки
Nn ≥
або
ε+<<ε− axa
n
як тільки n≥N. Отже,
ε<− ax
n
як тільки Nn ≥ ,
що доводить теорему.
Примітка
1. Слід зауважити, що ця теорема дає ознаку, за
якою можна встановити тільки існування границі числової послідо-
вності, але не можна знайти числове значення границі.
Примітка
2. Умова монотонності в розглянутій теоремі є
обов’язковою. Не всяка обмежена числова послідовність
(x
n
) має
границю. Так послідовність
1n
n
)1(x
−
−=
,
n
∈
N
є обмежена
)1x(
n
≤
, але границі немає.
Приклад 1. Довести, що послідовність
n2
n
21
1
...
21
1
21
1
x
+
++
+
+
+
=
збігається, тобто, що існує .xlim
n
n
∞→
Розв
’язування. Доведемо, що числова послідовність (x
n
) є зро-
стаючою. Справді,
,x
2
1
1
2
1
1
...
2
1
1
21
1
x
n
1nn2
1n
>
+
+
+
++
+
+
+
=
+
+
оскільки
.0
21
1
1n
>
+
+
З другого боку, використовуючи формулу
q1
qbb
S
n
11
n
−
−
=
(суми
n
- перших членів геометричної прогресії
...qb,...,qb,b
1n
11111
−
) маємо
.1
2
1
1
2
1
1
2
1
2
1
2
1
2
1
...
2
1
2
1
x
n
n
n2
n
<−=
−
⎟
⎠
⎞
⎜
⎝
⎛
−
=+++<
Звідси випливає, що послідовність
n
x
є обмеженою.
Отже, за попередньою теоремою робимо висновок, що задана
послідовність має границю.

194
Примітка 3. Зауважимо, що добуток
n
послідовних натура-
льних чисел
n...321 ⋅⋅⋅⋅ скорочено позначають !n , тобто
n...321!n ⋅⋅⋅⋅= і називають “ен факторіал”.
Приклад 2. Показати, що числова послідовність
!n
с
x
n
n
= , 0с > ,
n
∈
N
має границю, яка дорівнює нулю.
Розв
’язування. Послідовність (x
n
), починаючи з певного
значення
n
і для всіх його наступних значень, є спадною, оскільки
,
1n
c
x
1n
c
!n
c
)!1n(
c
x
n
n1n
1n
+
⋅=
+
⋅=
+
=
+
+
або
1n
c
x
x
n
1n
+
=
+
.
Звідси бачимо, що як тільки
c1n >+ , тобто 1cn −> , то
n1n
xx <
+
.
Крім того, послідовність
(x
n
) є обмеженою знизу, бо члени цієї
послідовності більші, наприклад, за нуль.
Отже, існує границя розглядуваної послідовності, причому
0
!n
c
lim
n
n
=
∞→
)0с( >
.
Справді, нехай
.аylim
n
n
=
∞→
Тоді
.аylim
1n
n
=
+
∞→
Перейшовши в рівності
1n
c
xx
n1n
+
⋅=
+
до границі, дістанемо
1
n
c
limxlimxlim
n
n
n
1n
n
+
⋅=
∞→∞→
+
∞→
або 0aa ⋅= .
Остання рівність можлива при
a=0, що треба було довести.
3.7. Нескінчено малі величини та їх властивості
Означення 1. Якщо числова послідовність (α
n
) має своєю
границею нуль (
)0lim
n
n
=α
∞→
, то така послідовність називається
нескінчено малою.
Наприклад,
n
1
n
=α
є нескінчено мала величина, тому що
.0
n
1
lim
n
=
∞→
Нескінчено малі величини будемо позначати
nnn
,,
γ
β
α .
Виходячи з означення границі числової послідовності
195
можна сформулювати еквівалентне означення нескінчено ма-
лої величини з означенням 1.
Означення 2. Числова послідовність
)(
n
α
називається не-
скінчено малою величиною, якщо для будь-якого наперед заданого
як завгодно малого додатного числа
0>ε існує такий номер
N
,
починаючи з якого виконується нерівність
,
n
ε<α як тільки
Nn ≥
.
Примітка. Нехай
.axlim
n
n
=
∞→
На основі означення границі чи-
слової послідовності можемо записати
ε<− ax
n
як тільки Nn ≥ . (3.12)
Якщо різницю
ax
n
−
позначити через
n
α
, тобто
nn
ax α=−
,
то ця різниця на основі означення 2 і (3.12) буде нескінчено малою,
бо
ε<α=−
nn
ax , коли
Nn ≥
.
І навпаки, якщо
ax
nn
−=α є нескінчено малою величиною,
тобто
ε<α
n
, коли Nn ≥ , то
n
x буде мати границею число
a
, бо
тоді
ε<− ax
n
, коли
Nn ≥
.
Висновок. Якщо послідовність
)x(
n
має границю число
a
,
то її загальний член можна подати у вигляді
nn
ax α+=
, де
n
α
–
нескінчено мала величина (
.0lim
n
n
=α
∞→
).
◙ Властивості нескінчено малих величин.
1. Алгебраїчна сума декількох нескінченно малих величин є
величина нескінченно мала.
2. Добуток нескінченно малої величини на величину обмеже-
ну є величина нескінченно мала.
3. Добуток сталої величини на нескінченно малу величину є
нескінченно мала величина.
4. Добуток двох нескінченно малих величин є величина
нескінченно мала.
§ 4. Границя функції
4.1. Означення границі функції
В багатьох прикладних задачах потрібно знайти значення
196
функції f(x) при прямуванні неперервного аргументу x до деякої то-
чки
0
x , в якій функція може бути і невизначена. Така поведінка фу-
нкції в деякій точці
0
x називається границею функції в точці
0
x .
Оскільки
0
x може бути як скінченим числом, та і дорівнювати
,
∞± то приведемо декілька означень границі функції.
Означення 1. Число
A
називається границею функції
)x(gy = , коли
∞→
x
і позначається
A)x(glim
x
=
∞→
, якщо для
довільного як завгодно малого додатного
0>ε можна вказати
таке додатне число
М
, що з нерівності Mx > випливає нерів-
ність
ε<− A)x(g .
Коли −∞→
x
, то означення границі функції аналогічне і ви-
користовують
позначення
A)x(glim
x
=
−∞→
.
Означення
2. Число
A
називається границею функції
)x(f
при
x
, що прямує до
0
x
, якщо для будь-якої послідовності
значень аргументу
,...,x,...,x,x
n21
збіжної до
0
x , відповідна пос-
лідовність значень функції
),...x(f),...,x(f),x(f
n21
збігається
до
A
.
Означення 3.
Число
A
називається границею функції
)x(f при
x
, що прямує до
0
x (
0
xx ≠ ), якщо для будь-якого мало-
го наперед заданого додатного ε можна вказати таке додатне
число
δ , що із нерівності δ<−
0
xx випливає нерівність
ε<− A)x(f
.
Коротко це означення записують так:
A)x(flim
0
xx
=
→
.
Слід відмітити, що теореми про границю суми, різниці, добут-
ку і частки для числових послідовностей (функцій цілочисельного
аргументу
),n(fx
n
=
n
∈
N
є справедливими і для функцій непе-
рервного аргументу, а саме:
ТЕОРЕМА. Нехай на множині X задані функції )x(f і
)x(
ϕ
, −
0
x гранична точка множини X і в точці
0
x обидві фун-
кції мають скінчені границі
а)x(flim
0
xx
=
→
,
.b)x(lim
0
xx
=
ϕ
→
Тоді
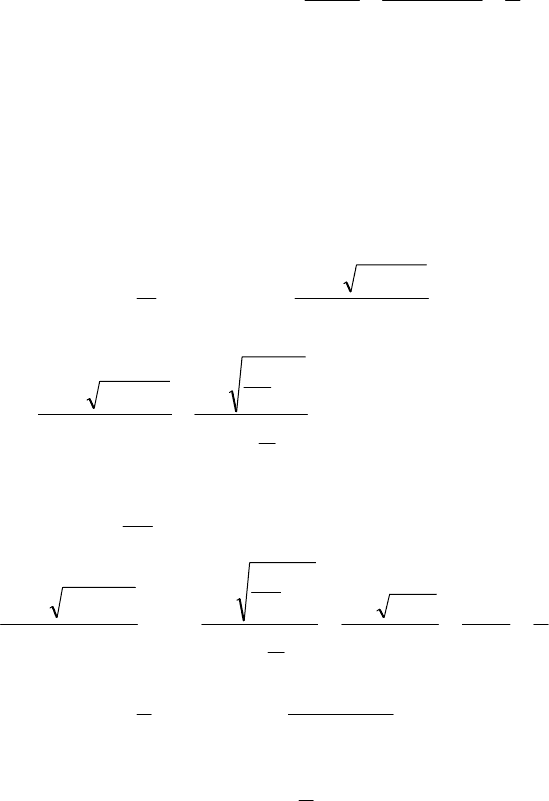
1)
;ba)x(lim)x(flim))x()x(f(lim
000
xxxxxx
±=
ϕ
±=
ϕ
±
→→→
197
2)
;ba)x(lim)x(flim)x()x(flim
000
xxxxxx
⋅=
ϕ
⋅=
ϕ
→→→
3) якщо
,0b)x(lim
0
xx
≠=
ϕ
→
то
.
b
a
)x(lim
)x(flim
)x(
)x(f
lim
0
0
0
xx
xx
xx
=
ϕ
=
ϕ
→
→
→
При знаходженні границь функції будемо користуватися тим,
що для основних елементарних функцій в будь-якій точці із області
визначення має місце рівність
),xlim(f)x(flim
00
xxxx →→
=
тобто
).x(f)x(flim
0
xx
0
=
→
Наприклад,
.x4x)x4x(flim
0
2
0
2
xx
0
+=+
→
Розглянемо декілька способів обчислення границь.
Приклад 1.
)(
∞
∞
. Знайти
8x5
x41x5
lim
2
x
+
++
∞→
.
Розв
’язування. Розділивши чисельник і знаменник на
x
, оде-
ржимо
.
x
8
5
4
x
1
5
8x5
x41x5
2
2
+
++
=
+
++
Тепер, використовуючи основні теореми про границі та домо-
вленість, що
0
x
a
lim
n
x
=
∞→
, n
∈
N, 0a ≠ , маємо
8x5
x41x5
lim
2
x
+
++
∞→
=
∞→x
lim .
5
7
5
25
05
405
x
8
5
4
x
1
5
2
=
+
=
+
++
=
+
++
Приклад 2.
)
0
0
(
. Знайти
.
6x5x
9x
lim
2
2
3x
+−
−
→
Розв
’язування. В результаті безпосередньої підстановки 3x =
у даний дріб маємо невизначеність (
)
0
0
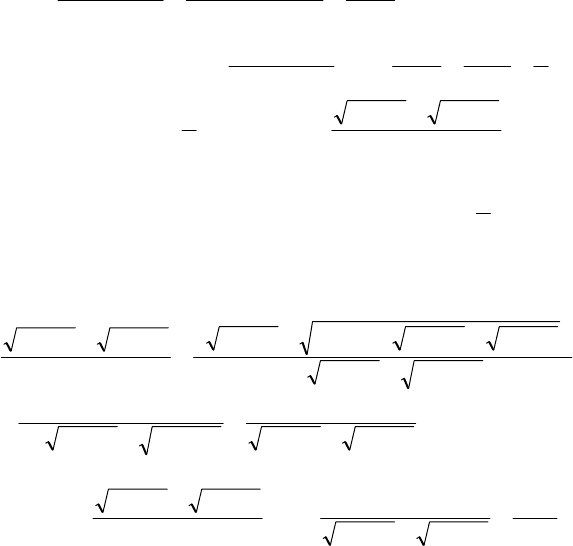
. Тому, використовуючи фо-
рмули розкладу, зробимо такі перетворення:
198
,
2x
3x
)3x)(2x(
)3x)(3x(
6x5x
9x
2
2
−
+
=
−−
−+
=
+−
−
.3x ≠
Таким чином,
.6
1
6
23
33
2x
3x
lim
6x5x
9x
lim
3x
2
2
3x
==
−
+
=
−
+
=
+−
−
→→
Приклад 3.
(
).
0
0
Знайти
x
x51x51
lim
0x
−−+
→
.
Розв
’язування. Аналогічно, як у прикладі 2, підстановка нуля
замість
x
у заданий вираз дає невизначеність ( )
0
0
. Перетворимо
дріб таким чином: помножимо чисельник і знаменник дробу на ви-
раз, спряжений до чисельника, а потім скоротимо дріб. В результаті
одержимо
)x51x51(x
)x51x51)(x51x51(
x
x51x51
−++
−++−−+
=
−−+
=
.
x51x51
10
)x51x51(x
x51x51
−++
=
−++
+−+
=
На основі одержаного результату маємо
.5
11
10
x51x51
10
lim
x
x51x51
lim
0x0x
=
+
=
−++
=
−−+
→→
4.2. Односторонні границі.
Нехай
−
0
x
точка числової осі. Зрозуміло, що запису
0
xx →
можна дати таке тлумачення: точки
x
наближаються до точки
0
x
зліва, коли
0
xx < і справа, коли
0
xx > . Отже, на числовій осі на-
ближення точок
x
до точки
0
x
може бути двостороннім. Якщо при
знаходженні границі функції
)x(f
при умові, що
0
xx →
і
x
приймає тільки значення менші від
0
x (більші від
0
x ) і якщо така
границя існує, то її називають лівостороньою (правостороньою)
границею функції
)x(f . Лівосторонні і правосторонні границі поз-
начають символом:
)0x(f)x(flim
0
0xx
0
−=
−→
))0x(f)x(flim(
0
0xx
0
+=
+→
.
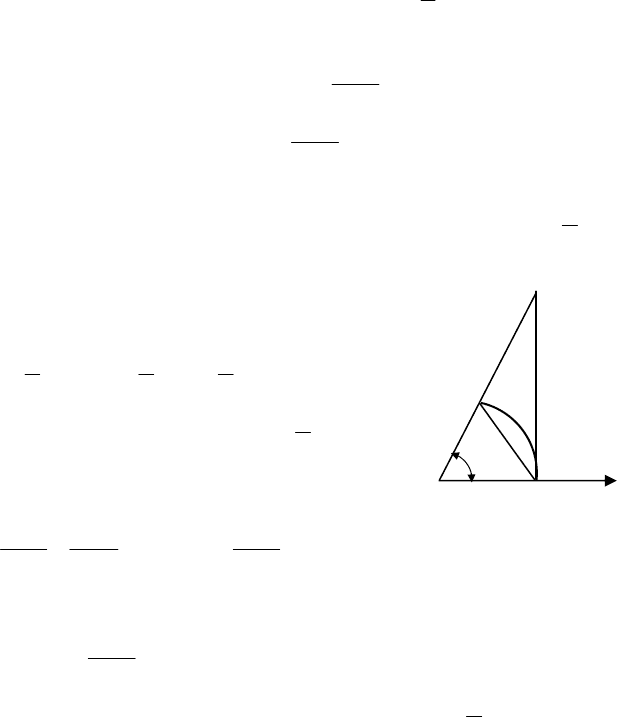
199
ТЕОРЕМА 1. Функція
)x(f
в точці
0
x
має границю тоді і
тільки тоді, коли в цій точці функція
)x(f має праву і ліву
)0x(f(
0
+
і
)0x(f(
0
−
) границі і права границя дорівнює лівій
границі
)).0x(f)0x(f(
00
−=+
4.3. Перша визначна границя
Для розкриття невизначеностей вигляду
( )
0
0
у тригонометри-
чних виразах користуються таким твердженням.
ТЕОРЕМА 2. Функція
x
xsin
)x(f =
при 0x → має грани-
цю, що дорівнює 1, тобто
1
x
xsin
lim
0x
==
→
- перша визначна гра-
ниця.
Доведення
. Якщо
x
є кут, виміряний у радіанах,
2
x0
π
<<
, то
(див. мал.) для площ трикутника
,OAB
сектора OAmB трикутника
OCB правильні нерівності
)ROBOA( ==
.
OCBOAmB.сектOAB
SSS
ΔΔ
<< або
tgxR
2
1
xR
2
1
xsinR
2
1
222
<< .
Після скорочення на число
2
R
2
1
діста-
немо
tgxxxsin << .
Поділивши почленно на
,xsin
знайдемо
x
cos
1
x
sin
x
1 <<
, звідси
.xcos
x
xsin
1 >>
Помноживши останню нерівність на (-1) і додавши (+1 ) до
кожної частини знайдених нерівностей, маємо
.xcos1
x
xsin
10 −<−<
Використовуючи нерівність
xxsin < )
2
x0(
π
<< і
перетворюючи вираз
,xcos1− знаходимо
В
С
О
А
m
х
х
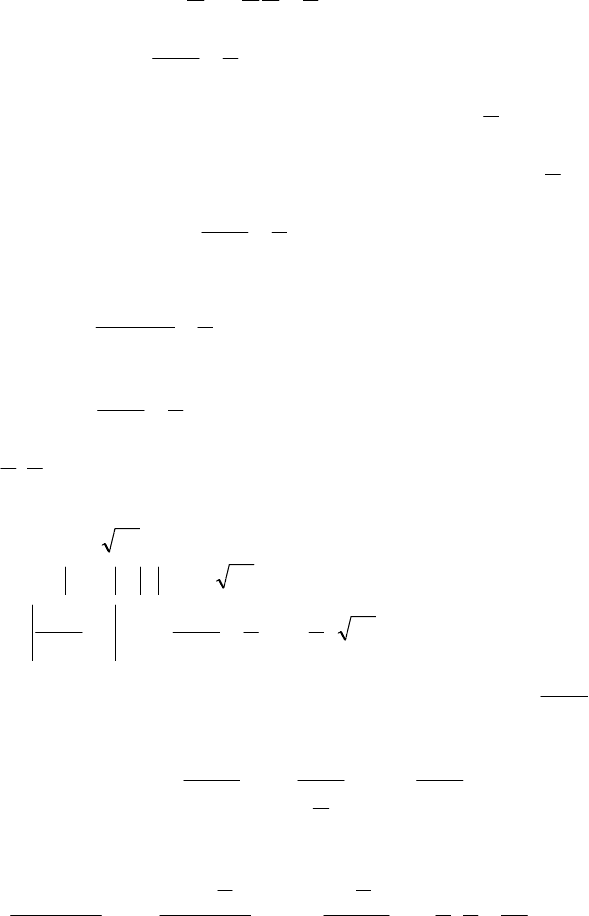
200
22
x
2
1
2
x
2
x
2
2
x
sin2xcos1 =<=−
.
Тому
2
x
2
1
x
xsin
10 <−<
. (A)
Покажемо правильність нерівностей (A) і для
0x
2
<<
π
−
.
Візьмемо допоміжну змінну
.
x
y
−= Оскільки
2
y0
π
<< , то за
доведеним вище
.y
2
1
y
ysin
10
2
<−<
Підставивши замість
y
число (-x), дістанемо
2
)x(
2
1
x
)xsin(
10 −<
−
−
−<
і, зважаючи на непарність функції
sinx, знайдемо
2
x
2
1
x
xsin
10 <−<
, тобто нерівність (А) правильна для всіх
),
2
,
2
(
ππ
−
0x ≠ .
Для наперед заданого числа
0>ε число 0>δ візьмемо таким,
що дорівнює
ε2 . Тоді з нерівностей
ε=δ<=−< 2x0x0 випливатиме нерівність
ε=ε<<−=−
22
)2(
2
1
x
2
1
x
xsin
11
x
xsin
.
А це означає, згідно означення 3, що границя функції
x
xsin
в
точці
x=0 дорівнює одиниці. Теорему доведено .
Приклад 1.
.a
y
ysin
lima
a
y
ysin
lim
x
axsin
lim
0y0y0x
===
→→→
Приклад 2.
.
2
25
2
5
2
5
2
x
x
2
5
sin
lim2
x
x
2
5
sin2
lim
x
x5cos1
lim
0x
2
2
0x
2
0x
=⋅⋅===
−
→→→
