Шинкарик М.І. Вища математика
Подождите немного. Документ загружается.


201
4.4. Допоміжні твердження
ТЕОРЕМА 3. Якщо
1x...xx
n21
=⋅⋅⋅ , де 0x
i
> ,
,n,...,2,1i =
то
nx
n
1i
i
≥
∑
=
, причому рівність має місце тільки тоді, коли
1x...xx
n21
====
.
ТЕОРЕМА 4. Середнє геометричне
n
додатніх чисел ,x
i
,n,...,2,1i = менше або дорівнює їх середньому арифметичному,
тобто
,
n
x...xx
x...xx
n21
n
n21
+++
≤⋅
причому рівність справ-
джується тільки тоді, коли
.x...xx
n21
===
Доведення
. Позначивши через
n
n21
x..xxq ⋅⋅= за теоремою 3
з рівності
1
q
x
...
q
x
q
x
n21
=⋅
випливає нерівність
n
q
x
...
q
x
q
x
n21
≥++ або
n
x...xx
q
n21
+++
≤
, причому рів-
ність має місце тільки тоді, коли
.x...xx
n21
===
Теорема доведе-
на.
4.5. Число
.
e
Друга визначна границя
Для розкриття невизначеності (1
∞
) використовують таке тве-
рдження:
ТЕОРЕМА 5. Послідовність
n
n
)
n
1
1(y +=
,
n
∈
N
має
границю.
Доведення
. Використовуючи твердження теореми 4, маємо
1n
1
1
1n
n)
n
1
1(1
)
n
1
1(1
1n
n
+
+=
+
⋅++
<+⋅
+
.
Звідси
1nn
)
1
n
1
1()
n
1
1(
+
+
+<+
,
тобто послідовність
n
n
)
n
1
1(y +=
,
n
∈
N
, монотонно зростає.

202
Аналогічно для послідовності
n
n
)
n
1
1(z −=
,
n
∈
N
, маємо
.
1n
1
1
1n
n)
n
1
1(1
)
n
1
1(1
1n
n
+
−=
+
⋅−+
<−⋅
+
Звідси
1nn
)
1
n
1
1()
n
1
1(
+
+
−<−
.
Таким чином, послідовність
n
n
)
n
1
1(z −=
,
n
∈
N
, також
монотонно зростає.
Оскільки
1n
1n)1n(1n1n
z
1
)
1n
1
1()
1n
n
()
n
1n
()
n
1
1(
+
+−+−++
=
+
−=
+
=
+
=+
,
то послідовність
1n
n
)
n
1
1(x
+
+= ,
n
∈
N
, спадає.
Тому
,4x)
n
1
1()
n
1
1(y
1
1nn
n
=≤+<+=
+
n
∈
N
.
Тобто
(y
n
)- обмежена послідовність і вище було показано , що
вона зростає.
Отже, послідовність
n
n
)
n
1
1(y +=
має границю. Цю границю
в математиці позначають буквою
e
, тобто
e)
n
1
1(lim
n
n
=+
∞→
.
Таку границю називають другою визначеною границею для
послідовностей. Доведено, що число
e – ірраціональне число і його
розклад в десятковий дріб з деякою точністю має вигляд
e
=2,718281828459045…
Логарифм числа
x>0 за основою e називається натуральним
логарифмом і позначається символом
ln x. Оскільки за означенням
логарифма правильна рівність
xln
ex = , то прологарифмувавши її за
основою 10, маємо
,xlnМxlg ⋅= де ....434294,0elgM == Число
M
називають модулем переходу від натурального логарифма до ло-
гарифма десяткового.
Далі доведемо існування границі функції
x
1
)x1()x(f +=
в

203
точці 0x = . Цю границю називають другою визначною границею
для власної функції.
ТЕОРЕМА 6. Правильна рівність .e)x1(lim
x
1
0x
=+
→
Доведення
. Спочатку доведемо рівність
.e)x1(lim
x
1
00x
=+
+→
Можемо вважати
1x0 ≤<
. Для кожного
x
∈
(
]
1,0
існує нату-
ральне число
)x(nn = таке, що
n
1
x
1
n
1
≤<
+
.
Звідси
n
1
1x1
1
n
1
1 +≤+<
+
+
.
Оскільки
n
x
1
1n ≥>+
, то
1n
x
1
x
1
n
)
n
1
1()
n
1
1()x1()
1
n
1
1()
1
n
1
1(
x
1
+
+<+≤+<
+
+≤
+
+
або
).
n
1
1()
n
1
1()x1(
1n
1
1
)
1n
1
1(
n
1n
x
1
+⋅+<+<
+
+
+
+
+
Якщо
00x +→ , то ∞→
n
. Крайні частини останніх нерівно-
стей мають границі при
∞→
n
, що дорівнюють числу
e
.
Звідси за теоремою 6 §3 і функція
x
1
)x1( + при 00x +→
матиме праву границю, що дорівнює
e
.
Покажемо, що і ліва границя функції
x
1
)x1( + в точці 0x =
дорівнює числу
e
. Введемо нову змінну
y
, зв’язану із змінною
x
рівністю
x
1
x
y
+
−=
.
Зазначивши, що
y1
y
x
+
−=
, дістанемо
).y1()y1()
y1
1
()
y1
y
1()x1(
y
1
y
1
1
y
y1
x
1
+⋅+=
+
=
+
−=+
−−
+
−
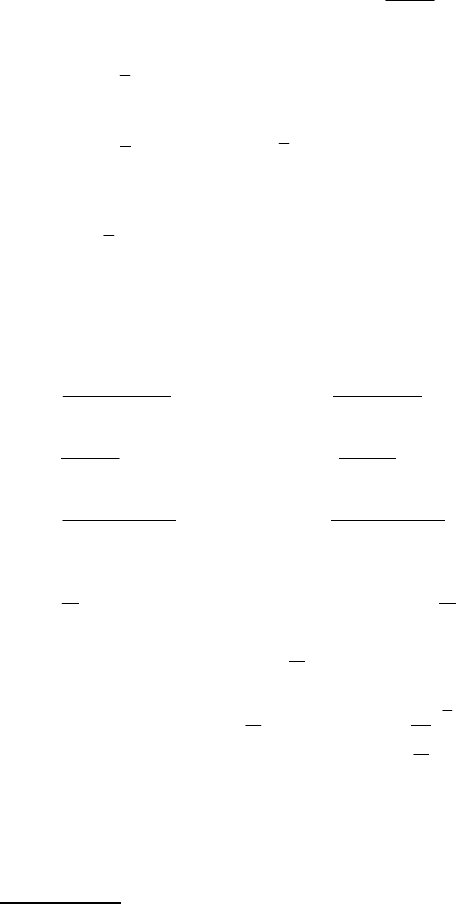
204
Якщо
x
прямує до нуля зліва, то
x
1
x
y
+
−=
прямує до нуля
справа. Звідси, враховуючи, що згідно доведеного вище твердження
,e)y1(lim
y
1
00
у
=+
+→
маємо
.e1e))y1()y1((lim)x1(lim
y
1
00y
x
1
00x
=⋅=++=+
+→−→
За теоремою 6 §3 випливає справедливість рівності
.e)x1(lim
x
1
0x
=+
→
Теорема 5 доведена.
Вправа. Виходячи з неперервності елементарних функцій
x
a
і
xlog
a
і, використовуючи другу визначну границю, довести справед-
ливість таких рівностей:
;elog
x
)x1(log
lim)a
a
a
0x
=
+
→
;1
x
)x1ln(
lim)
б
0x
=
+
→
;aln
x
1a
lim)
в
x
0x
=
−
→
;1
x
1e
lim)
г
x
0x
=
−
→
;
x
1)x1(
lim)
д
0x
α=
−+
α
→
.
x
1)x1(
lim)
е
0x
α=
−+
α
→
Примітка
. Другу визначну границю для функції
x
)
x
1
1()x(f +=
при
∞→
x
записують так:
.e)
x
1
1(lim
x
x
=+
∞→
Приклад 1. Знайти
.)
n
5
1(lim
n2
n
−
∞→
+=
Розв
’язування. .e))
5
n
1
1(lim()
n
5
1(lim
10
5
n
n
n2
n
10
−
∞→
−
∞→
=+=+=
−
4.6. Порівняння нескінчено малих величин
Нехай функція
y=f(x) визначена на проміжку (a,b) крім, мож-
ливо, точки х
0
∈
(a,b).
Означення1. Функція називається нескінчено малою в точ-
ці х
0
, якщо існує границя функції в даній точці і ця границя дорів-
нює нулю.
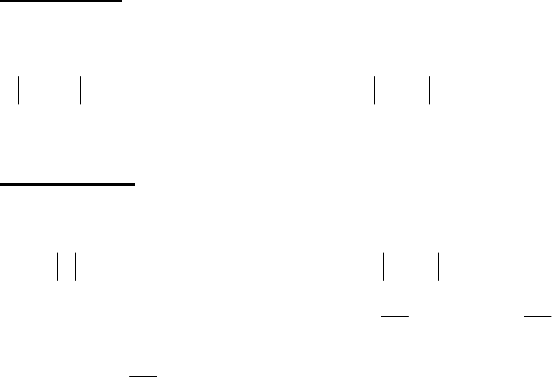
205
Нескінчено малу функцію в точці ще називають нескінче-
но малою величиною.
Приклад 1. Нехай
n
)x1(y −= . Тоді
.0)x1(lim
n
1x
=−
→
Отже, функція
n
)x1(y −= в точці
1x =
є нескінчено малою.
Приклад 2. Нехай
xsiny = . Тоді .0xsinlim
0x
=
→
Отже, задана
функція
xsiny =
в точці 0x = є нескінченно малою.
Якщо
0
x - внутрішня точка інтервалу
()
b,а , то, використа-
вши означення границі функції в точці, нескінчену малу функцію
можна означити так.
Означення 2. Функція )x(fy = називається нескінчено ма-
лою в точці
0
x
, якщо для будь-якого числа 0>ε існує число
0>δ таке, що для всіх
x
∈
()
b,а
0
xx ≠
, які задовольняють нері-
вність δ<−
0
xx , виконується нерівність ε<)x(f .
Аналогічно можна означити нескінчено малу функцію на не-
скінченості.
Означення 3. Функція
)x(fy =
називається нескінченно
малою на нескінченності ∞→x( ), якщо для будь-якого числа
0>ε
існує таке число
0M >
, що для всіх
x
, які задовольняють
нерівність Mx > , виконується нерівність ε<)x(f .
Приклад 3. Розглянемо функцію
2
x
1
y =
. Тоді
.0
x
1
lim
2
x
=
∞→
Отже, функція
2
x
1
y =
на нескінченності
)x( ∞→
є нескінчено ма-
лою.
Нескінченно малі функції аналогічно до нескінчено малих чи-
слових послідовностей володіють аналогічними властивостями.
Примітка
1. Іноді доводиться розглядати не одну, а кілька не-
скінченно малих функцій у даній точці. Такі функції порівнюють
між собою за допомогою границі їх відношення, і залежно від того
як поводить себе таке відношення поблизу даної точки, нескінченно
малим величинам дають певну назву.
Подамо ряд означень.
Нехай
)x(α і )x(
β
є нескінченно малі функції в точці
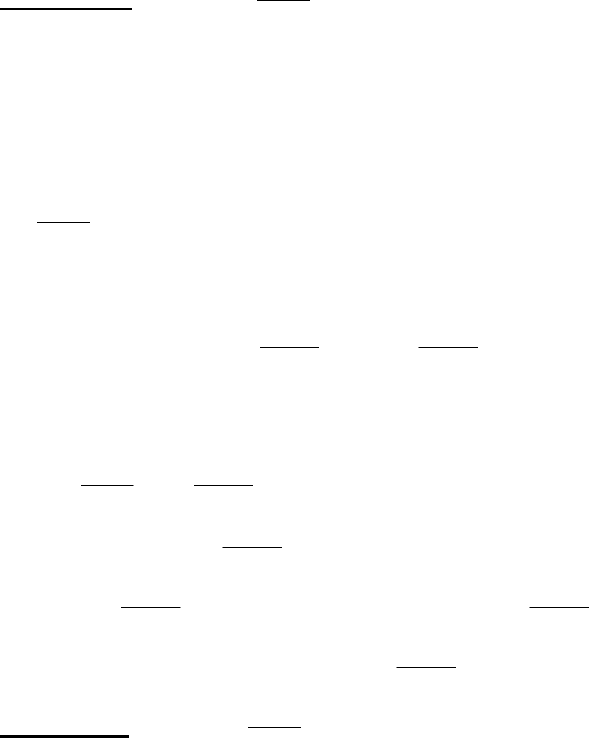
206
0
x ∈
()
b,а (
0
x може бути і нескінченно віддаленою точкою).
Означення 4. Якщо
0
)x(
)x(
lim
0
xx
=
β
α
→
, то )x(α називається
нескінченно малою вищого порядку малості, ніж
)x(
β
. При цьо-
му )x(
β
називається нескінченно малою нижчого порядку мало-
сті, ніж
)x(α
.
Приклад 4. Нехай
2
)1x()x( −=α , .1x)x( −=
β
Тоді )x(α
і
)x(
β
в точці
1x =
є нескінченно малі функції. Знайдемо
.0)1x(lim
)x(
)x(
lim
1x1x
=−=
β
α
→→
Отже, в цьому випадку )x(α є нескінчено мала вищого по-
рядку, ніж
)x(
β
.
Приклад 5. Нехай
1x
1
)x(
3
+
=α
, .
1x
1
)x(
2
+
=β
Тоді
,0)x(lim
x
=α
∞→
,0)x(lim
x
=
β
∞→
тобто )x(α і )x(
β
на нескінченності є нескінченно малі функції.
Знайдемо
.0
1x
1x
lim
)x(
)x(
lim
3
2
xx
=
+
+
=
β
α
∞→∞→
Отже, функція
1x
1
)x(
3
+
=α
є нескінченно мала вищого по-
рядку, ніж
1x
1
)x(
2
+
=β
при
∞→
x
або, що те саме,
1x
1
)x(
3
+
=β
є нескінчено мала нищого порядку, ніж
1x
1
)x(
3
+
=α
при
∞→
x
.
Означення 5. Якщо
,C
)x(
)x(
lim
0
xx
=
β
α
→
де С- відмінне від нуля
число, то )x(α і )x(
β
в точці
0
x
називаються нескінчено ма-
лими однакового порядку малості.
Якщо при цьому
1С = , то )x(α і )x(
β
в точці
0
x назива-
ються еквівалентними і записують
)x(α
~
)x(
β
(при
0
xx →
).
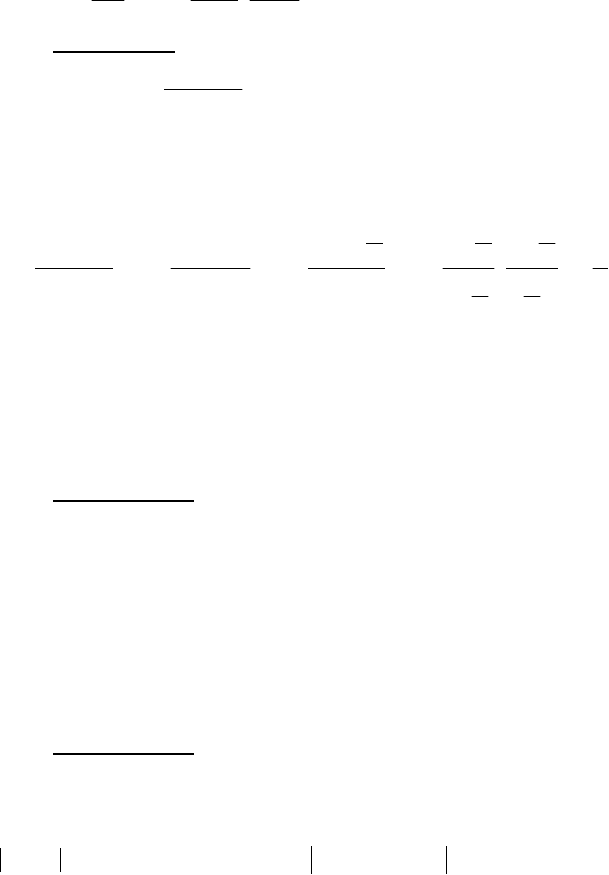
207
Приклад 6. Нехай
tgx)x( =α
, а
.x)x( =
β
Тоді
)x(α
і
)x(
β
в точці
0x = є нескінченно малі функції. Оскільки
,1)
xcos
1
x
xsin
(lim
x
tgx
lim
0x0x
=⋅=
→→
то
tgx
~
x
(при
)0x →
.
Означення 6. Якщо
)x(α
і
)x(
β
є нескінченно малі функції
в точці
0
x і
C
))x((
)x(
lim
k
xx
0
=
β
α
→
,де k - довільне число, а число 0C ≠ ,
то функція )x(α називається нескінченно малою порядку
k
по
відношенню до )x(
β
.
Приклад 7. Нехай
сosx1)x( −=α
, а
x)x( =
β
. Оскільки
,0
2
1
2
x
2
x
sin
2
x
2
2
x
sin
lim
x
2
x
sin2
lim
x
xcos1
lim
))x((
)x(
lim
0x
2
2
0x
2
0x
2
0x
≠==⋅
⋅
==
−
=
β
α
→→→→
то функція
сosx1)x( −=α
у точці 0x = є нескінченно малою дру-
гого порядку по відношенню до
.
x
§5. Неперервність функції
5.1. Означення неперервності функції в точці і на відрізку
Означення 1. Нехай функція f(x) визначена в околі
)x,x(
00
ε+ε− точки. Функція )x(fy = називається непере-
рвною в точці x
0
, якщо границя функції f(x) при
0
xx → існує і до-
рівнює значенню в точці
0
x
, тобто
).x(f)x(flim
0
xx
0
=
→
Це означення вимагає виконання таких трьох умов:
1.
f(x) повинна бути визначена в деякому околі точки x
0
.
2. Існує скінчена границя
).x(flim
0
xx→
3. Ця границя повинна дорівнювати значенню функції .
f(x
0
).
Означення 2. Нехай функція f(x) визначена в околі
)x,x(
00
ε+ε− точки
0
x . Функція )x(fy = називається непе–
рервною в точці x
0
., якщо для довільного як завгодно малого до-
датного ε , можна вказати таке ,0>δ що з нерівності
δ<−
0
xx випливає нерівність .)x(f)x(f
0
ε<−
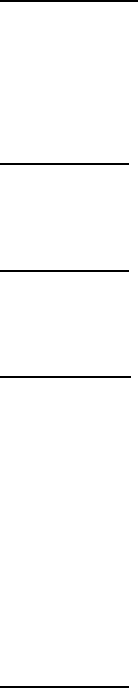
208
Якщо вираз
0
xxx −=Δ
назвати приростом аргументу
x
, а
вираз
)x(f)xx(fy
0
−Δ+=Δ - приростом функції, то на основі
означення 1 можна формулювати інше означення неперервності фу-
нкції
)x(f в точці
0
x .
Означення 3. Нехай функція )x(f визначена в околі
)x,x(
00
ε+ε− точки
0
x . Функція )x(fy = є неперервною в то-
чці
0
x , якщо в цій точці нескінчено малому приросту xΔ аргу-
менту
x
відповідає нескінчено малий приріст функції
)x(fy
0
Δ=Δ , тобто .0ylim
0x
=Δ
→Δ
Означення 4. Нехай функція
)x(f
визначена на проміжку
[]
.b,x
0
Функція )x(fy = називається неперервною зліва в точці
0
x , якщо
)x(f)x(flim
0
0xx
0
=
−→
.
Означення 5. Нехай функція )x(f визначена на проміжку
[]
.x,a
0
. Функція
)x(fy =
називається неперервною справа в то-
чці
0
x
, якщо
)x(f)x(flim
0
0xx
0
=
+→
.
Означення 6. Функція )x(fy = називається неперервною
на відрізку
[]
.b,a
, якщо вона неперервна в кожній точці інтер-
валу
).b,a(
Неперервна зліва в точці b )b(f)x(flim
0bx
=
−→
і непе-
рервна справа в точці
a
)a(f)x(flim
0ax
=
+→
.
Примітка
. Сума, різниця, добуток декількох неперервних в
деякій точці функцій є неперервні в цій точці. Якщо знаменник не
перетворюється в нуль у точці неперервності, то частка двох непе-
рервних в цій точці функцій є неперервною функцією.
5.2. Класифікація точок розриву функції
Означення 7. Якщо в точці
0
x
функція
)x(f
не є непере-
рвною, то точка
0
x
називається точкою розриву функції.
Виходячи з означення 1 неперервності функції
)x(fy = в
точці
0
x , точка
0
x буде точкою розриву функції, якщо не викону-
ється одна з трьох умов:
1) у точці
0
x функція )x(f невизначена;
209
х
2
1
-1
у
2) у точці
0
x
не існує границі
)x(flim
0
xx→
;
3) існує границя
)x(flim
0
xx→
, але вона не дорівнює значенню
функції
)x(f
0
.
Існують такі типи розривів :
1) Розрив 1-го роду. Якщо існу-
ють скінчені ліва і права границі
(
)x(flim
0xx
0
−→
і
)x(flim
0xx
0
+→
), але вони
не рівні між собою.
Наприклад, функція
⎩
⎨
⎧
>
<−
=
−
−
=
2x,1
,2x,1
2x
2x
y
має при
2x = розрив 1-го роду (див. мал.)
тому, що існують скінчені границі
,1ylim
02x
−=
−→
,1ylim
02x
=
+→
але ці
границі не рівні між собою.
2) Якщо лівостороння і правостороння гра-
ниці
)0x(f)x(flim
0
0xx
0
−=
−→
і
)0x(f)x(flim
0
0xx
0
+=
+→
в точці
0
x рівні між со-
бою, тобто
)0x(f)0x(f
00
+=− , але не дорів-
нюють значенню функції в точці
,x
0
тобто
)x(f)0x(f)0x(f
000
≠+=− .
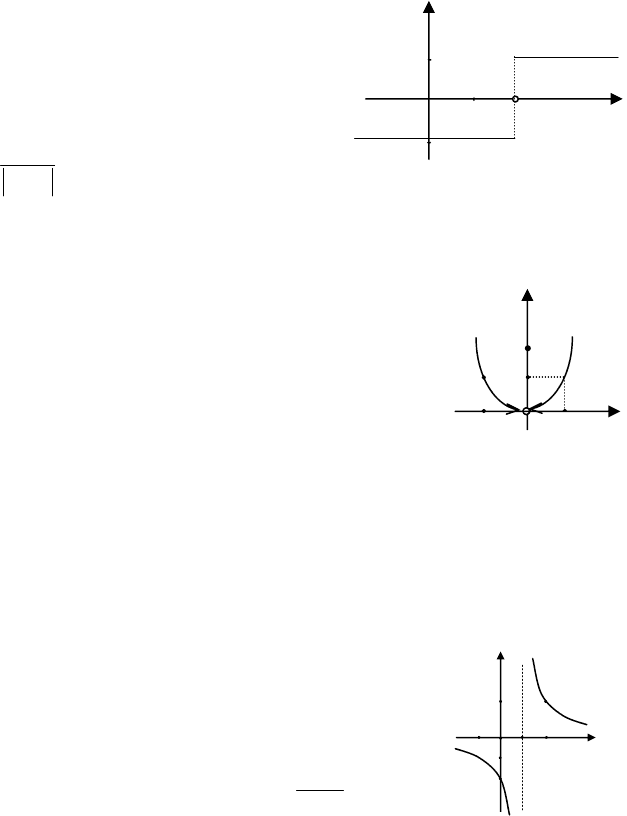
Наприклад, функція
⎩
⎨
⎧
=
≠
=
0x,2
,0x,x
)x(f
2
має в точці
0x = розрив, тому що ,0lim)x(flim
00x00x
==
+→−→
але ці
границі не дорівнюють значенню
2)0(f = в точці .0x =
Розрив
2-го роду. Якщо лівостороння або
правостороння границі функції
)x(f
у точці
0
x дорівнюють ∞± , то кажуть, що функція
)x(f має в точці
0
x розрив другого роду.
Наприклад, функція
1x
2
)x(f
−
=
має в то-
2
-1
1
1
х
у
1
1
-1
у
О
х
2
2
-2
-1

210
чці 1x = розрив 2-го роду, бо
,)x(flim
01x
−∞=
−→
.)x(flim
01x
+∞=
+→
§6. Властивості неперервних на відрізку функцій
6.1. Обмежені функції
Функції, неперервні на відрізку, мають ряд властивостей,
яких, взагалі кажучи, не мають функції, неперервні, наприклад, в
інтервалі. Ці властивості ми й розглянемо далі.
ТЕОРЕМА 1 (Вейєрштрасса). Неперервна функція на від-
різку обмежена на цьому відрізку, тобто існують такі два числа
m
і
M
, що M)x(fm ≤≤ для всіх
[]
b,ax∈ .
Доведення
. Доводячи за допомогою методу міркування від су-
противного, припустимо, що функція
)x(f , неперервна на відрізку
[]
b,a , не обмежена на цьому відрізку. Тому для кожного натураль-
ного
n
знайдеться точка
[]
b,ax
n
∈ така, що
,n)x(f > ,...2,1n =
Послідовність
)x(
n
обмежена. За відповідною теоремою ма-
тематичного аналізу з цієї послідовності можна виділити збіжну по-
слідовність
)x(
k
n
,
0n
xx
k
→
( ∞→k ) і точка
0
x належить
обов’язково відрізку
[]
b,a
, тому в ній функція
)x(f
неперервна,
якщо
()
b,ax
0
∈ , неперервна справа, якщо ax
0
= і неперервна зліва,
якщо
.bx
0
=
Отже, ми можемо записати такі два твердження:
,n)x(f
kn
k
>
,...,2,1k = і
),x(f)x(f
0n
k
→ ∞→k .
Звідси з першої нерівності випливає, що послідовність
))x(f(
k
n
необмежена, а з другого твердження випливає, що вона,
будучи збіжною, обмежена. Суперечність, до якої ми дійшли, дово-
дить теорему 1.
6.2. Існування найменшого і найбільшого значення
Нехай функція
)x(f визначена на множині
D
.
Значення
)x(f
∗
,
Dx ∈
∗
називається найменшим (найбіль-
