Шинкарик М.І. Вища математика
Подождите немного. Документ загружается.


241
випадку, коли в точці
0
x
функція набуває найменшого значення.
Теорема Ролля припускає просте геометричне тлумачення.
Якщо крива
AB
є графік функції )x(fy = на
[]
b,a ,
),b(f)a(f = то існує точка, в якій дотична до кривої паралельна
осі
Ox
(мал.6).
12.3. Теорема Лагранжа
Цю теорему ще називають теоремою про скінчені прирости.
ТЕОРЕМА
. Якщо функція
)x(fу =
неперервна на за-
мкнутому проміжку
[]
b,a і має похідну в кожній внутрішній то-
чці цього проміжку, то знайдеться принаймні одна така точ-
ка
сх = всередині проміжку, що справедлива рівність
)c('f)ab()a(f)b(f −=− . (4.5)
Доведення
. Розглянемо допоміжну функцію
.kx)x(f)x(F −=
Ця функція неперервна, як різниця двох неперервних функцій, а та-
кож має похідну у внутрішніх точках проміжку
[]
b,a , бо її мають
функції
)x(f та
.kx
Доберемо сталу k так, щоб ).b(F)a(F = Тоді
)x(F буде задовільняти всі умови теореми Ролля. Маємо
.kb)b(fka)a(f −=−
Звідки
a
b
)a(f)b(f
k
−
−
=
. (4.6)
Отже, при такому
k буде ).b(F)a(F =
Застосуємо до
)x(F
теорему Ролля . Знайдемо похідну
.k)x('f)x('F −=
Тоді існує точка
сх =
,
,bcа <<
що .0k)c('f)c('F =−=
Звідки
)c('fk=
. Підставивши це значення k у формулу (4.6), одер-
жимо
ab
)a(f)b(f
)c('f
−
−
=
або
).c('f)ab()a(f)b(f −=−
Теорема доведена.
Якщо покласти
0
xa = , xxb
0
Δ+= , то рівність (4.5) запи-
шеться у вигляді
)c('fx)x(f)xx(f
00
⋅Δ=−Δ+
, де
.xxcx
00
Δ+<<

242
Це означає, що приріст функції дорівнює приросту аргументу,
помноженому на похідну в деякій проміжній точці
с, що знаходить-
ся між
0
x і .xx
0
Δ+ Звідси і друга назва теореми.
З теореми Лагранжа випливає два важливих наслідки.
Наслідок 1. Якщо
похідна 0)x('f = на деякому інтервалі
()
,b,a
то функція
)x(f
стала на цьому проміжку.
Доведення. Нехай 0)x('f = на
()
,b,a а
1
x і
2
x - довільні
точки з цього проміжку. За теоремою Лагранжа
()
.0)c('fxx)x(f)x(f
1212
=−=−
Звідси,
),x(f)x(f
12
= а це означає, що .const)x(f =
Наслідок 2. Якщо
дві функції
)x(f
1
та
)x(f
2
мають одна-
кові похідні на деякому проміжку, то ці функції на ньому відрізня-
ються хіба що на сталу.
Доведення. Якщо )x('f)x('f
21
= на проміжку
()
,b,a то
функція
)x(f)x(f)x(F
2
1
−=
на підставі попереднього наслідку 1
дорівнює сталій:
,c)x(F = тому що .0)x('f)x('f)x('F
21
=−=
Отже,
c)x(f)x(f
21
=− або .c)x(f)x(f
21
+=
12.4. Теорема Коші
ТЕОРЕМА. Якщо дві функції
)x(f та )x(
ϕ
неперервні на
замкнутому проміжку
[]
b,a
і мають похідні
)x(f
′
та
)x(
ϕ
′
в
кожній внутрішній точці цього проміжку, причому
0)x( ≠
ϕ
′
в
кожній внутрішній точці проміжку, то існує принаймні одна та-
ка точка
с з цього проміжку, для якої виконується рівність
)c(
)c(f
)a()b(
)a(f)b(f
ϕ
′
′
=
ϕ−ϕ
−
.
Доведення
. Побудуємо допоміжну функцію
),x(k)x(f)x(F
ϕ
+= де k визначимо з умови, що
),b(F)a(F =
тобто
)b(k)b(f)a(k)a(f
ϕ
+=
ϕ
+
. Звідси,
,
)a()b(
)a(f)b(f
k
ϕ−ϕ
−
−=
тому що
0)a()b( ≠
ϕ
−
ϕ
. Це випливає з умови, що 0)x( ≠
ϕ
′
на
основі теореми Лагранжа.

243
Оскільки функція
)x(F
неперервна як сума неперервних фу-
нкцій на
[]
b,a і має похідну в кожній внутрішній точці
),b,a(
то
при цьому
k
)x(
)a()b(
)a(f)b(f
)x(f)x(F ϕ
ϕ−ϕ
−
−=
задовільняє всі умови теореми Ролля.
Отже, існує точка
),bca(с <<
така що
.0)c(F =
′
Знайдемо
).x(
)a()b(
)a(f)b(f
)x(f)x(F ϕ
′
ϕ−ϕ
−
−
′
=
′
Тоді
0)c(
)a()b(
)a(f)b(f
)c(f =ϕ
′
ϕ−ϕ
−
−
′
або
,
)c(
)c(f
)a()b(
)a(f)b(f
ϕ
′
′
=
ϕ−ϕ
−
що треба було довести.
12.5. Правило Лопіталя
Знаходження границь, які вимагають “розкриття
невизначеностей” типу
0
0
або
∞
∞
значно спрощується за допомогою
правила Лопіталя.
Правило Лопіталя. Якщо функції
)x(f і )x(g диференці-
йовані в околі точки
0
x
, за виключенням, можливо, самої точки
0
x
, причому в цьому околі
0)x('g ≠
і якщо
0)x(glim)x(flim
00
xxxx
==
→→
або
,)x(glim)x(flim
00
xxxx
∞==
→→
то
)x('g
)x('f
lim
)x(g
)x(f
lim
00
xxxx →→
=
.
Коротко це правило можна сформулювати так:
Для невизначеностей типу
0
0
або
∞
∞
границя відношення
двох функцій дорівнює границі відношення їх похідних, якщо
вона існує.
Доведемо першу частину цього правила.
Доведення
. Нехай функції )x(f і )x(g на деякому проміж-
ку
[]
b,a задовольняють умови теореми Коші і у внутрішній точці
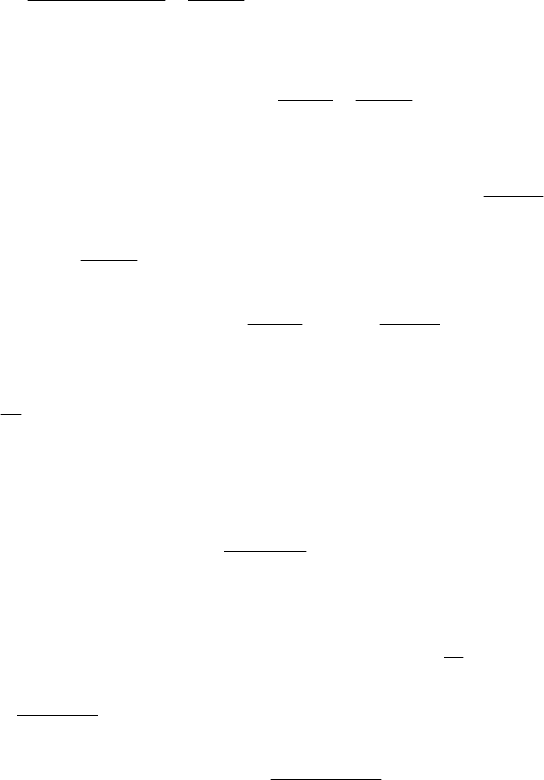
244
0
x цього проміжку 0)x(f
0
= і .0)x(g
0
= Візьмемо на
проміжку
[]
b,a яку-небудь точку
x
, відмінну від ,x
0
тобто
.xx
0
≠ Застосувавши теорему Коші, маємо
,
)c(g
)c(f
)x(g)x(g
)x(f)x(f
0
0
′
′
=
−
−
де
c
- точка, що знаходиться між
0
x та
.
x
Оскільки за припущен-
ням
,0)x(g,0)x(f
00
== то
)c(g
)c(f
)x(g
)x(f
′
′
=
.
Якщо
x
прямує до
0
x
, то і
c
буде прямувати до
0
x
, бо
c
міститься між
0
x і
.
x
Таким чином, якщо існує
)x(g
)x(f
lim
0
xx
′
′
→
, то
існує
)c(g
)c(f
lim
0
xc
′
′
→
, які рівні. Звідси випливає, що
.
)x(g
)x(f
lim
)x(g
)x(f
lim
00
xxxx
′
′
=
→→
Випадок, що в такий спосіб розкривається невизначеність ти-
пу
∞
∞
вимагає більш складних міркувань і доводиться в більш пов-
них курсах вищої математики.
Зауваження. Відмітимо, що умова про існування границі по-
хідних є суттєвою.
Наприклад,
1
xsinx
xsinx
lim
x
=
+
−
∞→
і виконані умови
∞=+=−
∞→∞→
)xsinx(lim)xsinx(lim
xx
. Про те застосувати правило
Лопіталя при розкритті цієї невизначеності типу
∞
∞
неможливо, бо
xcos1
xcos1
lim
x
+
−
∞→
не існує.
Приклад. Обчислити
.
2x3x
)4x(tg
lim
2
2
2x
+−
−
→

245
Розв’язування. Підстановка 2x = в даний вираз дає невизна-
ченість
.
0
0
Застосуємо правило Лопіталя:
.4
)322(1
22
)3x2()4x(cos
x2
lim
)'2x3x(
))'4x(tg(
lim
2x3x
)4x(tg
lim
22
2x
2
2
2x
2
2
2x
=
−⋅⋅
⋅
=
−⋅−
=
=
+−
−
=
+−
−
→
→→
§13. Формула Тейлора
Важливою задачею математичного аналізу є знаходження
значень функцій, заданих формулами. Безпосередньо ми можемо
обчислити значення функцій, заданих многочленами, чи дробово-
раціональними функціями. Так, наприклад, знайдемо значення фун-
кцій: а)
4x5xy
2
+−= , при 2x = , б)
3x4
1x2
z
2
+
−
=
, при 2x = .
Отримаємо:
24252)2(y
2
=+⋅−= ,
19
3
324
122
)2(z
2
=
+⋅
−⋅
=
.
Тоді як значення функцій
xlny,xsiny == знайти безпосеред-
ньо не можемо.
В розв’язанні цієї задачі може допомогти формула Тейлора.
Встановимо цю формулу для многочленів.
13.1. Формула Тейлора для многочлена
Нехай задано многочлен
n
n
2
210
xc...xcxcc)x(f ++++=
і деяке число
a
. Покажемо, що даний многочлен можна записати у
вигляді:
n
n
2
210
)ax(A...)ax(A)ax(AA)x(f −++−+−+= (4.7)
знайдемо значення постійних
.A,...,A,A,A
n210
Підставивши
a
x
=
в (4.7), одержимо
0
A)a(f = .
Продиференціюємо (4.7):
1n
n21
)ax(nA...)ax(2A1A)x(f
−
−⋅++−⋅+⋅=
′
(4.8)
Поклавши в (4.8)
a
x
= , одержимо
.1A)a(f
1
⋅=
′
Звідси,
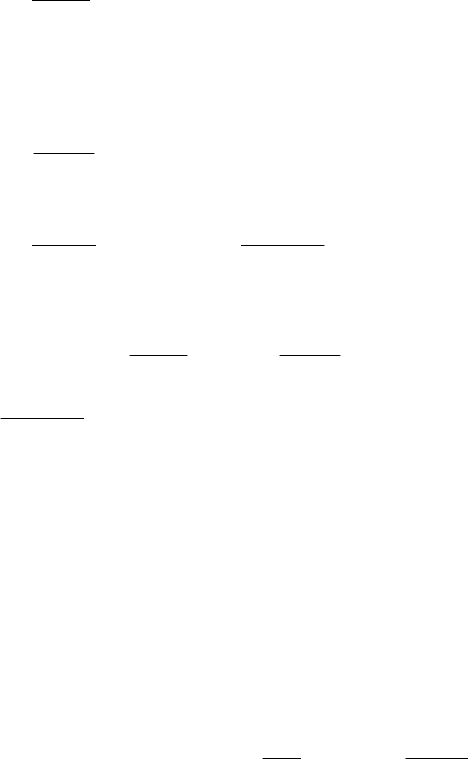
246
!
1
)a(f
A
1
′
=
.
Продиференціюємо (4.8):
2n
n32
)ax)(1n(nA...)ax(23A12A)x(f
−
−−⋅++−⋅⋅+⋅⋅=
′′
.
Поклавши тут
,
a
x
=
одержимо ,12A)a(f
2
⋅⋅=
′′
звідки
!
2
)a(f
A
2
′′
=
.
Продовжуючи такі міркування, одержимо
!
3
)a(f
A
3
′′′
=
і взагалі
!
n
)a(f
A
)n(
n
= .
Отже, для будь-якого многочлена і будь-якого
a
справед-
лива формула
++−
′′
+−
′
+= ...)ax(
!
2
)a(f
)ax(
!
1
)a(f
)a(f)x(f
2
,)ax(
!n
)a(f
n
)n(
−+
яка називається формулою Тейлора для многочлена.
Приклад. Нехай
.5x4x2x)x(f
23
−−+= Розкласти за
степенями
.2x −
Розв
’язування:
,5x4x2x)x(f
23
−−+= 3524222)2(f
23
=−⋅−⋅+= ,
,4x4x3)x(f
2
−+=
′
1642423)2(f
2
=−⋅+⋅=
′
,
4x6)x(f +=
′′
, 16426)2(f =+⋅=
′′
,
,6)x(f =
′′′
.6)2(f =
′′′
Тому,
.)2x()2x(8)2x(163
)2x(
321
6
)2x(
21
16
)2x(1635x4x2x
32
3223
−+−+−+=
=−
⋅⋅
+−
⋅
+−+=−−+
13.2. Формула Тейлора для довільної функції
Нехай
−)x(f будь-яка функція, неперервна, що має непере-
рвні похідні всіх порядків на проміжку (
β
α, ). Візьмемо яке- небудь
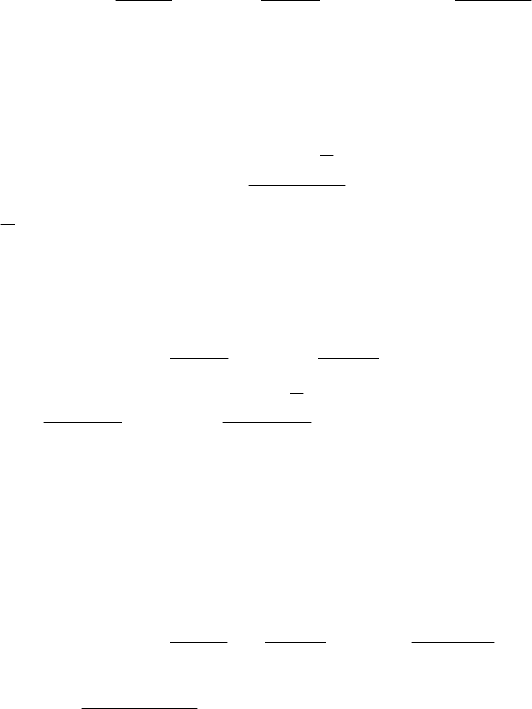
247
a
з цього проміжку та будь-яке натуральне число
n
і складемо
многочлен
,)ax(
!
n
)a(f
...)ax(
!
2
)a(f
)ax(
!
1
)a(f
)a(f)x(T
n
)n(
2
n
−++−
′′
+−
′
+=
який будемо називати тейлоровським многочленом нашої функції.
Вважаємо, що
)x(f не може дорівнює ).x(T
n
Проте досить
часто різниця між ними виявляється малою. Позначимо її
).x(R
n
Одержимо
).x(R)x(T)x(f
nn
+=
Доведено, що
)x(R
n
можна
виразити формулою
,)ax(
)!1n(
)x(f
)x(R
1n
)1n(
n
+
+
−
+
=
де
x проміжна точка між
a
і
.
x
Ця формула задає залишковий
член
R
n
(x) в формі Лагранжа. Доведення її виходить за рамки нашо-
го курсу і тому не приводиться.
Отже, для довільної функції маємо формулу
()
,)ax(
)!1n(
xf
)ax(
!n
)a(f
...)ax(
!2
)a(f
)ax(
!1
)a(f
)a(f)x(f
1n
)1n(
n
)n(
2
+
+
−
+
+−+
++−
′′
+−
′
+=
яка називається формулою Тейлора з залишковим членом у формі
Лагранжа.
13.3. Формула Маклорена
Взявши у формулі Тейлора
,0a =
одержимо формулу Мак-
лорена
),x(Rx
!n
)0(f
...x
!2
)0(f
x
!1
)0(f
)0(f)x(f
n
n
)n(
2
+++
′′
+
′
+=
де ,x
)!1n(
)x(f
)x(R
1n
)1n(
n
+
+
+
θ
=
де θ число .10 <θ<
Ця формула найчастіше використовується для зображення
функцій.
Приклад. Знайти формулу Маклорена для функції
,xsin)x(f = взявши 8n = .
Розв
’язування: Обчислимо
,xsin)x(f = ;0)0(f =
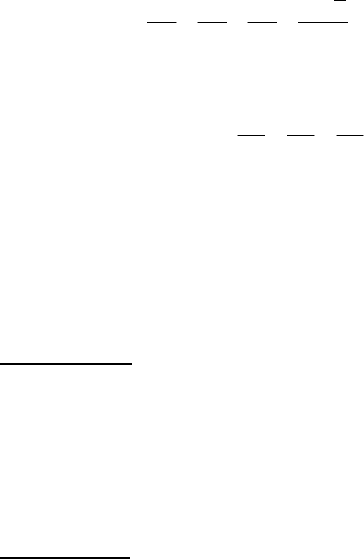
248
,xcos)x(f =
′
;1)0(f =
′
,xsin)x(f −=
′′
;0)0(f =
′′
,xcos)x(f −=
′′′
;1)0(f −=
′′′
,xsin)x(f
IV
=
0)0(f
IV
=
.
Зауваживши, що значення похідних дальше повторюються,
одержимо
.x
!9
xcos
!7
x
!5
x
!3
x
xxsin
9
753
+−+−=
Враховуючи, що величина залишкового члена досить мала,
можемо написати наближену формулу
.
!
7
x
!
5
x
!
3
x
xxsin
753
−+−≈
Обчислюючи синус якого-небудь кута, вираженого в граду-
сах, треба спочатку перетворити їх в радіани і тоді підставляти у
формулу. Приклади на використання подібних формул буде показа-
но в іншому розділі.
§14.Зростання і спадання функції на проміжку
Означення 1. Функція
)x(f
називається зростаючою на
проміжку
()
,b,a якщо більшому значенню аргументу х відповідає
більше значення функції. Тобто, якщо
2
1
xx <
, то
).x(f)x(f
21
<
Якщо нерівність виконується нестрога, ),x(f)x(f
21
≤ то
функція називається неспадною.
Означення 2. Функція )x(f називається спадною на про-
міжку
()
,b,a
якщо більшому значенню аргументу х відповідає
менше значення функції. Тобто, якщо
21
xx <
, то
).x(f)x(f
21
>
Якщо нерівність виконується нестрого,
),x(f)x(f
21
≥
то
функція називається незростаючою.
14.1 Необхідна умова зростання та спадання функцій

249
ТЕОРЕМА. Якщо диференційована функція на проміжку
()
b,a зростає, то її похідна невід’ємна, а якщо спадає, то її похід-
на недодатна.
Доведення
. Якщо функція )x(fy = зростає, то з означення
прирости
xΔ і yΔ будуть однакових знаків. Тому відношення
.0
x
y
>
Δ
Δ
А .0)x('f
x
y
lim
0x
≥=
Δ
Δ
→Δ
У випадку, коли функція
)x(fy =
спадає, прирости xΔ і
yΔ різних знаків, їх відношення від’ємне, а похідна .0)x('f ≤
14.2Достатні умови зростання і спадання функції
ТЕОРЕМА
. Якщо неперервна на замкненому проміжку
[]
b,а
функція
)x(f
має всередині цього проміжку додатну по-
хідну, то функція зростає, а якщо від’ємну, то функція спадає.
Доведення
. Нехай
0)x('f >
при .bxa << Візьмемо дві точ-
ки
1
x та
2
x )xx(
21
< з проміжку
()
,b,a і застосуємо до функції
f(x) теорему Лагранжа. Одержимо
).c('f)xx()x(f)x(f
1212
−=−
Оскільки
0xx
12
>−
,
0)c('f >
за умовою теореми, то цей
добуток також більший нуля, а тому
,0)x(f)x(f
12
>−
або
).x(f)x(f
12
> Це означає, що функція )x(f зростає.
Аналогічно доводиться друга частина теореми.
Проміжки зростання і спадання функцій називаються
проміжками монотонності функцій.
Для їх визначення знаходять похідну функції, прирівнюють її
до нуля і знаходять корені похідної. Цими коренями розбивають
область визначення функції на проміжки. В кожному з проміжків
беруть всередині точку і встановлюють знак похідної в них.
В тих
проміжках, де похідні додатні, функція зростає, а де від’ємні – спа-
дає.
Приклади. Знайти проміжки зростання і спадання функцій:
а)
;x3x
3
x
y
2
3
−−=
б)
y=lnx.
Розв
’язування.
250
а) Область визначення функції – вся числова вісь (-
),∞∞
.
Знаходимо похідну:
.3x2xy
2
−−=
′
Шукаємо корені похід-
ної:
,03x2x
2
=−−
16344D =⋅+=
,
,1
2
42
x
1
−=
−
= .3
2
42
x
2
=
+
=
Наносимо ці корені на числову пряму. Область визначення
вони поділяють на три проміжки (мал.7).
Знаходимо знаки похідної в кожному з зазначених проміжків,
обчисливши значення похідної в деяких точках кожного проміжка:
Отже, функція зростає на проміжках:
),,3()1,( ∞−−∞ ∪ спадає на проміжку (-1;3).
б) Область визначення тільки додатні числа (
0; )∞ .
.1xln
x
1
xxln)x(lnxxln)x(y −=⋅−=
′
−
′
=
′
Знаходимо корені похідної
01xln =− , 1xln = ,
e
x
=
.
Наносимо цей корінь на промінь, що зо-
бражає область визначення (мал.8).
Встановлюємо знаки похідної в цих про-
міжках:
.01121eln)e(y
,011011ln)1(y
22
>=−=−=
′
<−=−=−=
′
Отже, функція спадає на проміжку
),e;0(
зростає на проміж-
ку
).;e( ∞
§15. Екстремум функції
15.1. Поняття екстремуму
Будемо розглядати неперервні функції, які не змінюються мо-
нотонно, тобто такі, які на окремих проміжках зростають, а на ін-
ших спадають. Графіки таких функцій схематично можна зобразити
малюнком 9.
.0538163424)4(f
.03)0(f
.053443)2(2)2()2(f
2
2
>=−−=−⋅−=
′
<−=
′
>=−+=−−−−=−
′
3
+
-
+
Мал.7
-1
е
-
+
Мал.8
0
