Шинкарик М.І. Вища математика
Подождите немного. Документ загружается.

261
точки другого роду:
01x,0e)1x(
2
2
x
2
2
=−=−
−
,
,1x
1
−=
.1x
2
=
Ці точки розбивають область визначення функції на проміж-
ки:
),1(),1,1(),1,( ∞−−−∞
(мал.15). Знаходимо знаки другої
похідної в цих проміжках.
Отже, точки
,1x
1
−=
1x
2
= є точками перегину. На
проміжку
−− )1,1( крива опукла,
на проміжках
),1()1,( ∞∪−−∞ -
крива вгнута (мал.16).
§19. Асимптоти графіка функції
При дослідженні функцій часто буває, що графіки їх як за-
вгодно близько наближаються до цієї чи іншої прямої. З такими лі-
ніями ви зустрічалися при вивченні гіперболи.
Означення 1. Пряму лінію називають асимптотою графіка
функції ),x(fy = якщо відстань точки
M
графіка від цієї прямої
прямує до нуля при віддаленні точки
M
в нескінченість.
Асимптоти бувають вертикальними, похилими і горизонталь-
ними.Вертикальні асимптоти існують тоді, коли функція має розри-
ви другого роду.
Означення 2. Якщо в точці
0
xx = хоч одна з
односторонніх границь
∞=
+→
)x(flim
0xx
0
або
∞=
−→
)x(flim
0xx
0
, то
пряма
0
xx = є вертикальною асимптотою.
Наприклад, для функції .
x
1
y =
−∞==
−→−→
x
1
limylim
00x00x
і .
x
1
limylim
00x00x
∞==
+→+→
Отже,
0x = - вертикальна асимптота (мал.17).
Означення3. Якщо існує скінчена
границя ,bylim
x
=
±∞→
то пряма
by =
називається горизонтальною асимптотою.
Мал
.1
-
1
1
+
-
+
Мал.16
-
1
1
1
х
у
О
x
y
0
Мал.1
262
Оскільки для функції
x
1
y =
маємо ,0
x
1
limylim
xx
==
∞→∞→
то пря-
ма
0y = - горизонтальна асимптота.
Рівняння похилої асимптоти шукають у вигляді прямої з куто-
вим коефіцієнтом
.bkxy += Відстань точки )y,x(M графіка фун-
кції
)x(fy = приблизно можна виразити через різницю ординат
при одному і тому значенні
x
:
).bkx()x(fd +−=
За означенням асимптоти
0d → при
,
x
±∞→ тобто
[]
0bkx)x(flim
x
=−−
±∞→
. (4.9)
Розділивши цю рівність на
x
,маємо
.0
x
b
k
x
)x(f
lim
x
=
⎥
⎦
⎤
⎢
⎣
⎡
−−
±∞→
Оскільки
,0
x
b
lim
x
=
±∞→
то
x
)x(f
limk
x ±∞→
= . (4.10)
Якщо границя (4.10) не існує, то похилої асимптоти не буде.
Якщо
k скінчене число, то з (4.9) знайдемо
[]
.kx)x(flimb
x
−=
±∞→
Таким чином, одержимо рівняння похилої асимптоти
y=kx+b.
При
0k =
маємо рівняння горизонтальної асимптоти .by =
Приклад. Знайти асимптоти графіка функції
.
x
3x2x
y
2
−+
=
Розв
’язування. Область визначення функції
).
;0()0;( ∞∪−∞
+∞=
⎥
⎦
⎤
⎢
⎣
⎡
−+=
−+
=
−→−→−→
x
3
2xlim
x
3x2x
limylim
00x
2
00x00x
,
.
x
3
2xlim
x
3x2x
limylim
00x
2
00x00x
−∞=
⎟
⎠
⎞
⎜
⎝
⎛
−+=
−+
=
+→+→+→
Отже,
x=0 - вертикальна асимптота.
Знаходимо похилі асимптоти
y=kx+b
.1
x
3
x
2
1lim
x
3x2x
lim
x
)x(f
limk
2
x
2
2
xx
=
⎟
⎠
⎞
⎜
⎝
⎛
−+=
−+
==
∞→∞→∞→
263
=
−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−+
=−=
∞→∞→∞→
x
3x2
limx
x
3x2x
lim)kx)x(f(limb
x
2
xx
.2
x
3
2lim
x
=
⎟
⎠
⎞
⎜
⎝
⎛
−=
∞→
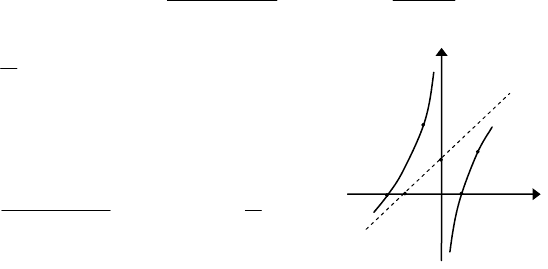
Отже, 2xy += - похила
асимптота (мал.18).
Горизонтальних асимптот нема,
оскільки
∞=
⎟
⎠
⎞
⎜
⎝
⎛
−+=
−+
=
∞→∞→∞→
x
3
2xlim
x
3x2x
limylim
x
2
xx
.
§20.Загальна схема дослідження функції і
побудова її графіка
Графік заданої функції можна будувати по довільно взятих
точках. При такому способі можна не виявити всіх особливостей її
графіка.
Провівши попередньо дослідження, ми шукаємо характерні
для даного графіка точки і тим спрощуємо розв’язок задачі про по-
будову графіка.
При дослідженні
функції і побудові її графіка доцільно
дотримуватися такої схеми:
Перший етап (використання виду заданої функції).
1). Знаходимо область визначення функції, точки розриву;
2). Досліджуємо функцію на парність чи непарність, періоди-
чність;
3). Знаходимо асимптоти графіка функції;
4). Знаходимо точки перетину графіка функції з осями коор-
динат.
Другий етап (використання похідної першого порядку).
5).
Знаходимо критичні точки першого роду, інтервали
зростання і спадання, точки екстремумів та екстремальні значення
функції.
Третій етап (використання похідної другого порядку).
6). Знаходимо критичні точки другого роду, інтервали опук-
лості і вгнутості, точки перегину та значення функції в цих точках.
2
О
х
Мал.1
8
у
1

264
Четвертий етап. Складемо таблицю результатів дослідження.
Наносимо отримані точки, асимптоти на координатну площи-
ну і будуємо графік функції з урахуванням точок розриву, інтерва-
лів зростання та спадання функцій, проміжків опуклості та вгнутості
графіка функцій.
Приклад 1. Дослідити функцію
y=x
3
−3x
2
та побудувати її
графік.
Розв
’язування.
1) Область визначення функції : вся числова вісь
(−∞,∞)
2). Функція ні парна ні непарна, оскільки
23
x3x)x(y −−=− , а тому ).x(y)x(y)x(y −≠≠−
Функція не періодична.
3). Вертикальних асимптот графік немає, бо нема точок роз-
риву.
Дослідимо чи графік має похилі асимптоти
:bkxy +=
.)x3x(lim
x
x3x
lim
x
y
limk
2
x
23
xx
∞=−=
−
==
∞→∞→∞→
Похилих асимптот графік також немає.
4). Знайдемо точки перетину графіка функції з осями коорди-
нат: при
;0y,0x == тобто точка );0;0(O
при
0y =
0x0)3x(x0x3x
223
=⇒=−⇒=−
і ,3x =
тобто точка
).0;3(M
Другий етап.
5). Знаходимо похідну першого порядку:
).2x(x3x6x3y
2
−=−=
′
Знаходимо критичні точки першого роду:
.2x,0x,0)2x(x3
21
===−
Критичні точки розбивають область визначення на проміжки
(−∞,0)∪(0,2)∪(2,∞) (мал.19). Знаходимо знаки похідної в цих про-
міжках:
,09)23(33)3(y >=−⋅=
′
,03)21(13)1(y <−=−⋅=
′
.09)21)(1(3)1(y >=−−−=−
′
Отже, функція зростає на проміжках
);2()0,( ∞∪−∞ , спадає на
проміжку
)2;0(
.
2
+
0
-
+
Мал
.19
265
В точці 0x = функція має максимум,
.0)0(yy
max
==
В точці
x=2 функція має мінімум,
.4128232)2(yy
23
min
−=−=⋅−==
Третій етап.
6). Знаходимо похідну другого порядку:
).1x(66x6y −=−=
′′
Знаходимо критичні точки другого ро-
ду:
,0)1x(6 =−
.1x = Критична точка 1x = розбиває область ви-
значення на проміжки:
),1()1,( ∞∪−∞ (мал.20).
Знаходимо знаки другої похідної в цих проміжках:
.06)12(6)2(y
,06)10(6)0(y
>=−=
′′
<−=−=
′′
Отже, графік функції опуклий на про-
міжку
)1;(−∞ , вгнутий на проміжку );1( ∞ . Точка
1x =
є точкою
перегину,
.231131)1(yy
23
.
пер
−=−=⋅−==
7). Складемо таблицю, де занесемо всі результати дослі-
дження
Знайдемо ще додатково
.4)1(3)1()1(y
23
−=−⋅−−=−
Наносимо всі характерні точки
на координатну площину і буду-
ємо графік (мал.21).
х (-∞;0)
0 (0;1)
1 (1;2)
2 (2:∞)
у
′
+ 0 - - - 0 +
у
′
′
- -6 - 0 + 6 +
у
Ê
∩
0
макси-
мум
Ì
∩
-2
перегин
Ì
∪
-4
мінімум
Ê
∪
1
-
+
Мал.20
-2
у
х
4 3 2
-1
1
О
-4
1
Мал.21
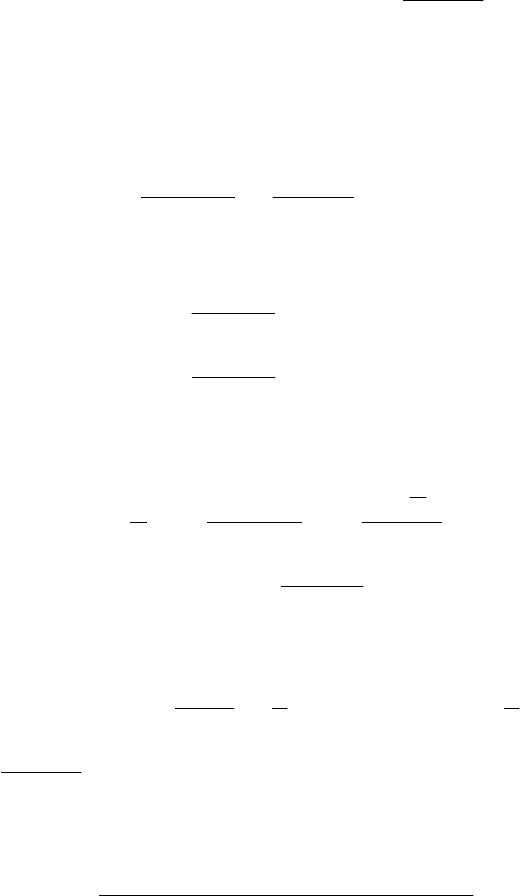
266
Приклад 2. Дослідити функцію
2
)2x(
6x2
y
−
−
=
та побудувати її
графік.
Розв
’язування. Перший етап.
1). Область визначення функції
).;2()2;( ∞∪−∞ Функція має
розрив в точці
.2x =
2). Функція ні парна ні непарна, оскільки
22
)2x(
6x2
)2x(
6x2
)x(y
+
+
−=
−−
−−
=−
і ).x(y)x(y)x(y −≠≠−
Функція неперіодична.
3) Оскільки в точці розриву
2x = ,
−∞=
−
−
=
−→−→
2
02x02x
)2x(
6x2
limylim
, а
,
)2x(
6x2
limylim
2
02x02x
+∞=
−
−
=
+→+→
то пряма
2x =
- вертикальна
асимптота.
Дослідимо чи графік має похилі асимптоти
:bkxy +=
0
)2x(
x
6
2
lim
)2x(x
6x2
lim
x
y
limk
2
x
2
xx
=
−
−
=
−
−
==
∞→∞→∞→
.
0
)2x(
6x2
lim)kxy(limb
2
xx
=
−
−
=−=
∞→∞→
.
Отже,
0y = - горизонтальна асимптота.
4). Знайдемо точки перетину графіка функції з осями коорди-
нат: при
,
2
3
)2(
6
y,0x
2
−=
−
−
==
тобто точка
)
2
3
;0(M
0
−
; при
,0y =
,3x,0
)2x(
6x2
2
==
−
−
тобто точка
).0;3(M
1
Переходимо до другого етапу:
5). Знайдемо похідну першого порядку:
=
−
−
′
−−−
′
−
=
′
4
22
)2x(
)6x2())2x(()2x()6x2(
y
267
.
)2x(
x28
)2x(
12x44x2
)2x(
)6x2(2)2x(2
)2x(
)6x2)(2x(2)2x(2
33
34
2
−
−
=
−
+−−
=
=
−
−−−
=
−
−−−−
=
Знаходимо критичні точки першого роду:
.4x;0x28;0
)2x(
x28
3
==−=
−
−
Враховуючи точку
x=2, де похі-
дна не існує, розіб’ємо область визна-
чення на проміжки
)8;4()4;2()2,( ∪∪−∞ (мал.22) і встановимо
знаки першої похідної в цих проміжках:
;06
1
6
)21(
28
)1(y
3
<−=
−
=
−
−
=
′
;0
)23(
328
)3(y
3
>
−
⋅−
=
′
.0
27
2
)25(
528
)5(y
3
<−=
−
⋅−
=
′
Отже, функція зростає на проміжку
)4;2( , спадає на проміж-
ках
).;4()2;( ∞∪−∞ В точці 4x = функція має максимум,
2
1
4
2
)24(
642
)4(yy
2
max
==
−
−⋅
==
. Маємо точку ).
2
1
;4(M
2
Переходимо до третього етапу:
6). Знаходимо другу похідну:
.
)2x(
20x4
)2x(
x6244x2
)2x(
)x28(3)2x(2
)2x(
)x28()2x(3)2x(2
)2x(
)x28())2x(()2x()x28(
y
44
46
23
6
33
−
−
=
−
+−+−
=
=
−
−−−−
=
−
−−−−−
=
=
−
−
′
−−−
′
−
=
′′
Знайдемо критичні точки другого роду:
.5x;020x4;0
)2x(
20x4
4
==−=
−
−
Враховуючи точку
2x = , де
y
′′
не існує, розбиваємо область ви-
значення на проміжки:
);5()5;2()2;( ∞∪∪−∞
(мал.23).
5 2
-
-
+
Мал.23
4 2
-
+
-
Мал.22
268
4
9
Встановимо знаки другої похідної в цих проміжках:
,0
4
5
16
20
)2(
20
)0(y
4
<−=−=
−
−
=
′′
,08
1
8
)23(
2034
)3(y
4
<−=−=
−
−⋅
=
′′
.0
64
1
4
4
)26(
2064
)6(y
44
>==
−
−⋅
=
′′
Отже, графік функції опуклий на проміжках:
)5;2()2;( ∪−∞ , вгну-
тий на проміжку
).;5( ∞ Точка 5x = є точкою перегину,
.
9
4
)25(
652
)5(yy
2
.пер
=
−
−⋅
==
Маємо точку ).
9
4
;5(M
3
7). Складемо таблицю, де занесемо результати дослідження
(-∞;0)
0 (0;2)
2 (2;3)
3 (3;4)
4
(4;5)
5
(5:∞)
у
′
- - -
не
існує
+ + + 0
- -
-
у
′
′
- - -
не
існує
- - - - - 0
+
у
Ì
∩
2
3
−
Ì
∩
не
існує
Ê
∩
0
Ê
∩
0,5
Ì
∩
Ì
∪
висновок
Функція
Спадає,
Графік
Опук-
лий
точка
перетину
з віссю
Оу
Функція
спадає,
графік
опуклий
вертикальна
асимптота
Фунція
Зростає,
Графік
Опуклий
точка
перетину
з віссю
Ох
Функція
зростає,
графік
опуклий
Точка
переги
-
н
у
Функція
спадає
графік
опуклий
максимум
Функція
спадає,
графік
опуклий
Будуємо графік (мал.24).
О
х
2
3
−
2 4
у
3
5
Мал.24
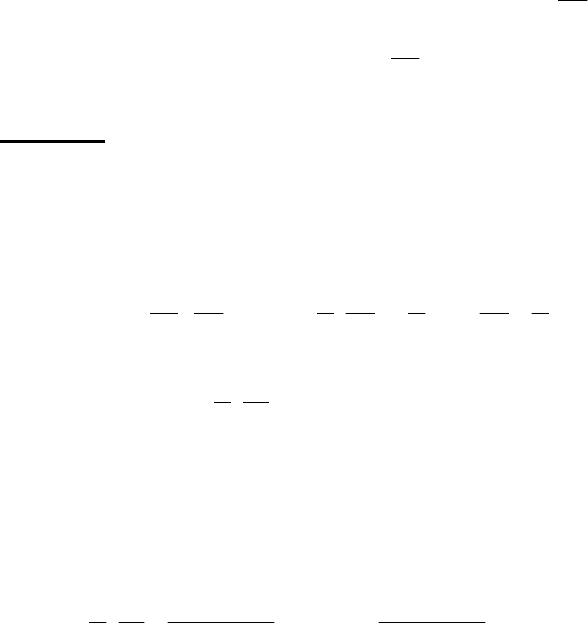
269
§21. Еластичність функції
В економічних дослідженнях прирости тих чи інших
показників, що характеризують економічні процеси найчастіше
виражають у відсотках до базових значень. Тому і зміну величин,
які зв’язані з ними функціональною залежністю також виражають у
відсотках. Для цього використовують поняття еластичності функції,
яке виражається через похідну функції.
21.1. Означення і
властивості еластичності функцій
Нехай задана функція
)x(fy =
. Якщо аргумент
x
одержав
приріст
xΔ і при цьому функція
y
одержала приріст yΔ , то
x
xΔ
називають відносним приростом аргумента, а
y
yΔ
- відносним при-
ростом функції.
Означення. Границя відношення відносного приросту функ-
ції до відносного приросту аргумента при умові, що приріст ар-
гумента прямує до нуля, якщо існує, називається еластичністю
функції.
Позначають еластичність функції
)x(fy = відносно змінної
x
)y(E
x
. Тобто,
).x(f
y
x
x
y
lim
y
x
x
y
y
x
lim
x
x
:
y
y
lim)y(E
0x0x0x
x
′
=
Δ
Δ
=
⎟
⎠
⎞
⎜
⎝
⎛
Δ
Δ
⋅=
⎟
⎠
⎞
⎜
⎝
⎛
ΔΔ
=
→Δ→Δ→Δ
Отже, якщо в точці
x
функція має похідну, то еластичність визна-
чається формулою
.
dx
dy
y
x
)y(E
x
⋅=
Еластичність виражає наближений відсоток приросту функції,
який відповідає 1% приросту аргумента.
Приклад. Знайти еластичність функції
7x4xy
2
+−=
і обчи-
слити її при
.5x,2x,1x ===
Розв
’язування.
.
7x4x
)4x2(x
)4x2(
7x4x
x
dx
dy
y
x
)y(E
22
x
+−
−
=−
+−
=⋅=
270
,0
784
)44(2
)/y(E
,5,0
4
2
7141
)412(1
)/y(E
2x
2
1x
=
+−
−
=
−=−=
+⋅−
−⋅
=
=
=
.5,2
72025
)452(5
)/y(E
5x
=
+−
−⋅
=
=
Отже, якщо
x
зросте на 1% з 1 до 1,01, то
y
спаде на 0,5%.
Якщо
x
зросте на 1% з 2 до 2,02, то значення змінної
y
практично
не зміниться. Якщо
x
зросте на 1% з 5 до 5,05, то
y
зросте на 2,5%.
◙ Властивості еластичності функції
ТЕОРЕМА 1. Еластичність добутку двох функцій
дорівнює сумі еластичностей співмножників:
).V(E)U(E)VU(E
xxx
+=⋅
Доведення
. За означенням еластичності
).V(E)U(E
V
Vx
U
Ux
)UVVU(
UV
x
)UV(
UV
x
)VU(E
xx
x
+=
=
′
+
′
=
′
+
′
=
′
=⋅
ТЕОРЕМА 2. Еластичність частки двох функцій дорівнює
різниці показників еластичності діленого і дільника:
)V(E)U(E
V
U
E
xxx
−=
⎟
⎠
⎞
⎜
⎝
⎛
.
Доведення
. За означенням еластичності
).V(E)U(E
V
xV
U
Ux
V
VU
U
U
x
V
UVVU
U
Vx
V
U
V
U
x
V
U
E
xx
2
x
−=−
′
=
=
⎟
⎠
⎞
⎜
⎝
⎛
′
−
′
=
′
−
′
⋅=
′
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
21.2. Еластичність попиту відносно ціни
В аналізі і прогнозах цінової політики застосовується поняття
еластичності попиту і пропозиції.
Нехай
p
ціна одного виробу, а Q- кількість виробів,
вироблених і проданих за деякий час, що визначає попит. Величина
Q залежить від ціни, тобто Q є функцією від
p
: ).p(f=Q
