Шинкарик М.І. Вища математика
Подождите немного. Документ загружается.

311
Розділ 6. ІНТЕГРАЛЬНЕ ЧИСЛЕННЯ ФУНКЦІЙ
ОДНІЄЇ ЗМІННОЇ
Одним з основних завдань розділу ІV диференціальне числен-
ня функцій однієї змінної, є завдання знаходження похідної від
заданої функції. Розділ математики, який розв’язує обернену задачу
– знаходження функції за її похідною (інтегрування), а також інші
задачі, які безпосередньо зв’язані з інтегруванням називається
інтегральним численням. Предметом вивчення даного розділу є
інтеграли: визначений, невизначений, поверхневий, криволінійний,
подвійний, потрійний і інші, їхні властивості, методи знаходження,
їх застосування до розв’язування різних задач.
Інтегральне числення практично виникло із задач обчислення
площ і об’ємів різних фігур і тіл. Вперше такі задачі намагались
розв’язати вчені Стародавньої Греції
(Евдокс Кнідський, Архімед та
ін.). В ХVІ - ХVІІ ст.., інтенсивний промисловий розвиток в Європі
привів до розвитку інтегрального числення та його застосування.
Праці вчених І. Кеплера, Б. Кавальєрі, П. Ферма, Е. Торрічеллі, Дж.
Валліса, Б. Паскаля, Х. Гюйгенса поглибили теоретичні основи
інтегрального числення. Вчені І. Ньютон та Г.
Лейбніц створили ряд
загальних методів знаходження інтегральних сум. Їх праці багато
задач інтегрального числення звели до суто технічного рівня. Г.
Лейбніц ввів зручну символіку, яка застосовується і тепер. А фор-
мула Ньютона-Лейбніца, яка зв’язала невизначений і визначений
інтеграли, є центральною формулою інтегрального числення. По-
дальший історичний розвиток інтегрального числення
пов’язаний з
іменами І. Бернуллі, Л. Ейлера, П. Чебишева, О. Коші, В. Буня-
ковського. Суттєвими для розвитку інтегрального числення є роботи
видатного українського математика М.В. Остроградського.
(12.09.1801-20.12.1861, народився в с. Пашенівка, Козельського р-ну
Полтавської обл.),. Навчався в Харківському університеті, де його
вчителями були Т.Ф. Осиповський та А
.Ф. Павловський. Під час
перебування в Парижі слухав лекції А.М.Ампера, О.Л.Коші,
П.С.Лапласа, С.Д.Пуассона, Ж.Б.Ж.Фур’є. Друг В.Я.Буняковського.
Перебуваючи в Петербурзі потоваришував з Т. Г. Шевченком.
Основні праці М.В. Остроградського стосуються математичної
фізики, математичного аналізу (формула зв’
язку інтеграла по об’єму
з інтегралом по поверхні, принцип розкладності функцій в ряд за
власними функціями, принцип локалізації для тригонометричних
312
рядів, правило перетворення змінних в подвійних інтегралах, метод
інтегрування раціональних функцій і ін.), теоретичної механіки.
Розв’язав деякі задачі з теорії чисел, алгебри, диференціальних
рівнянь, теорії рядів.
§ 1. Невизначений інтеграл
1.1. Первісна функція та невизначений інтеграл
Задача знаходження для функції f(x) такої функції F(x), що
)x(f)x(F =
′
є основною задачею інтегрального числення.
Операція інтегрування (знаходження інтегралу
) є оберненою
операцією до диференціювання ( знаходження похідної). Термін
інтеграл походить від латинського integer – цілий. Деколи вжива-
ють термін – антипохідна
.
Означення 1. Функція F(x) називається первісною для
функції f(x), якщо для довільного х з області визначення f(x),
)x(f)x(F =
′
або
.dx)x(f)x(dF =
(6.1)
Наприклад,
а) для
,xcos2)x(f =
первісною є
,xsin2)x(F =
тому, що
).x(fxcos2)xsin2()x(F ==
′
=
′
б) для
3
x4)x(f = , - ,x)x(F
4
= тому що
).
x(fx4)x()x(F
34
==
′
=
′
Відшукання первісної є операція неоднозначна. Так
,5x)x(F
4
+=
3,24x)x(F
4
−=
і
179x)x(F
4
+=
і т.д.і взагалі,
,Cx)x(F
4
+=
де С - довільне стале число є первісні для
3
x4)x(f =
.
ТЕОРЕМА 1. Якщо
)x(F
1
та )x(F
2
- дві первісні для
функції
f(x) на відрізку
[]
,b;a то різниця між ними дорівнює
сталому числу.
Доведення. Нехай
)x(f)x(F
1
=
′
і )x(f)x(F
2
=
′
. Тоді
0))x(F)x(F()x(F)x(F
2121
=
′
−=
′
−
′
, а значить, за наслідком з
теореми Лагранжа про скінченні прирости, що
С)x(F)x(F
21
=− , або С)x(F)x(F
21
+= . (6.2)
313
Означення 2. Сукупність усіх первісних для функції f(x)
називається невизначеним інтегралом від цієї функції і
позначається
∫
+= C)x(Fdx)x(f . (6.3)
При цьому
)x(f)x(F =
′
, f(x) - називається підінтегральною
функцією,
dx)x(f -підінтегральним виразом,
∫
- знак невизначе-
ного інтеграла.
Операція відшукання первісної для даної функції називається
інтегруванням. Таким чином, невизначений інтеграл - це множина
всіх функцій, похідна яких дорівнює підінтегральній функції, а ди-
ференціал дорівнює підінтегральному виразу.
Базовою для інтегрального числення є така теорема:
ТЕОРЕМА 2. Якщо функція неперервна, то для неї існує
первісна, отже і
невизначений інтеграл.
(Доводиться в фундаментальних
курсах вищої математики). З
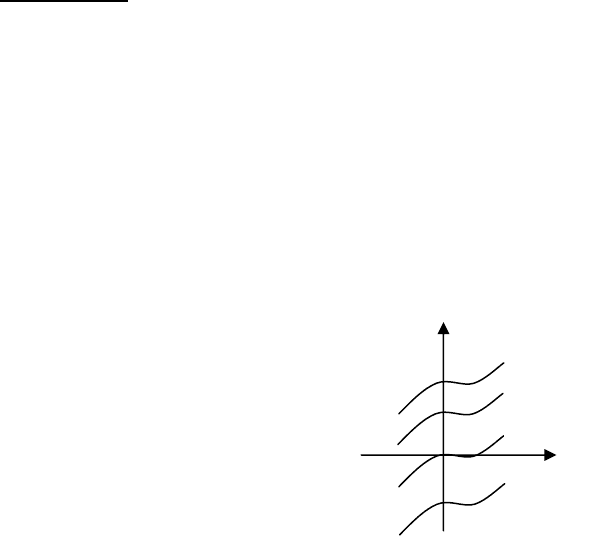
геометричної точки зору невизначений
інтеграл - це сім’я кривих, кожна з яких
утворюється зсувом однієї з них пара-
лельно собі вверх або вниз. (мал. 1)
1.2. Основні властивості невизначеного інтеграла
ТЕОРЕМА 3. (Властивість 1) Похідна від невизначеного
інтеграла дорівнює підінтегральній функції.
()
)x(fdx)x(f =
′
∫
(6.4)
Доведення. Згідно з означенням (6.2)
∫
+= ,C)x(Fdx)x(f
а тому
()
()()()
)x(fC)x(FC)x(F
dx)x(f
=
′
+
′
=
′
+=
′
∫
.
Отже похідна від первісної дорівнює підінтегральній функції.
ТЕОРЕМА 4. (Властивість 2) Диференціал від невизначе-
ного інтеграла дорівнює підінтегральному виразу
()
dx)x(fdx)x(fd =
∫
(6.5)
Доведення. За означенням диференціала
dx)x(f))x(f(d
′
=
.
Тому
y
1
=F(x)+С
1
x
y
2
=F(x)+С
2
y
y=F(x)
Мал. 1
314
()
()()
dx)x(fdx)x(F)x(FdC)x(Fddx)x(fd =
′
==+=
∫
.
ТЕОРЕМА 5. (Властивість 3) Невизначений інтеграл від
диференціала деякої функції
F(x) дорівнює цій функції з
точністю до довільної сталої,
()
C)x(F)x(Fd +=
∫
. (6.6)
Доведення. Продиференціюємо ліву і праву частини рівності.
Одержимо:
()()
dx)x(f)x(Fd)x(Fdd ==
∫
і
dx)x(fdx)x(F))x(F(d)С)x(F(d =
′
==+
.
Праві частини рівностей однакові. Значить рівні й ліві. Теоре-
му доведено.
Аналогічно, диференціюванням лівої і правої частин рівності,
доводяться теореми 6 і 7.
ТЕОРЕМА 6. (Властивість 4). Сталий множник можна ви-
носити за знак невизначеного інтеграла.
∫∫
= dx)x(fkdx)x(kf
(k=const) (6.7)
ТЕОРЕМА 7. (Властивість 5) Інтеграл від алгебраїчної су-
ми скінченого числа функцій дорівнює алгебраїчній сумі
інтегралів від цих функцій
()
∫∫∫
±=± dx)x(fdx)x(fdx)x(f)x(f
2121
. (6.8)
1.3. Таблиця невизначених інтегралів
Інтегрування є операція, обернена до диференціювання. Тому
формули інтегрування отримують з формул для знаходження похід-
них. А універсальність застосування формул інтегрування випливає
з теореми про незалежність вигляду невизначеного інтеграла від
вибору аргументу (інваріантність невизначеного інтеграла відносно
змінної інтегрування ).
ТЕОРЕМА 8. Нехай
f(x) – деяка неперервна функція на
даному проміжку,
х – незалежна змінна, F(x) – її первісна,
∫
+= C)x(Fdx)x(f
і нехай )x(u
ϕ
= неперервно диференційо-
вана функція. Тоді
∫
+= C)u(Fdu)u(f
. (6.9)
Доведення. Розглянемо інтеграл
∫∫
′
= dxu)u(fdu)u(f
. В
цьому випадку складна функція
))x((F)u(F
ϕ
=
є первісна для f(u).
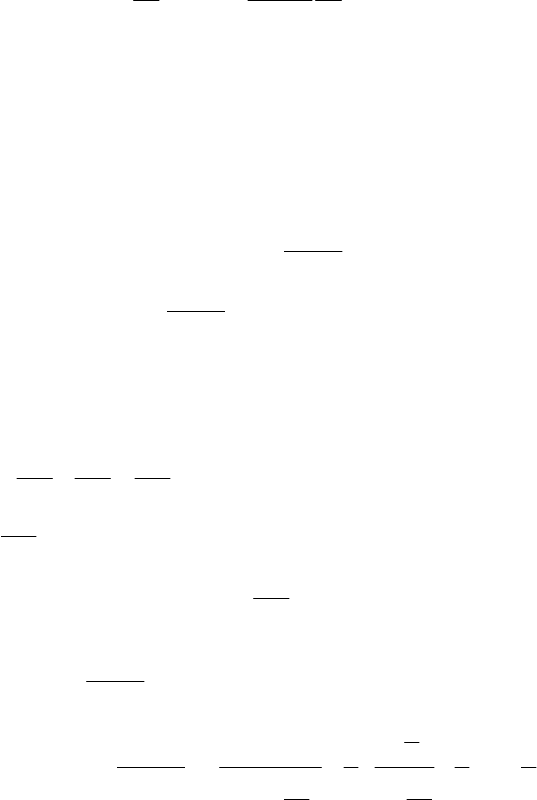
315
Справді, внаслідок незалежності диференціала першого по-
рядку від вибору незалежної змінної, одержуємо
du)u(fdu)u(F)u(dF =
′
= . При цьому
[]
u)u(f
dx
du
du
)u(dF
)u(F
dx
d
′
==
.
Тому, з справедливості формули (6.3), випливає справедли-
вість формули
∫
+= C)u(Fdu)u(f . (6.9)
Отже формулами інтегрування можна користуватись при
будь-якій змінній інтегрування. Використовуючи таблицю дифере-
нціалів основних елементарних функцій, виведемо деякі формули
інтегрування. Інші виводяться аналогічно.
1) Інтегруючи формулу
ucos
du
dtgu
2
=
одержимо
∫
+= Ctgu
ucos
du
2
. (6.10)
2) В випадку показникової функції, використовуємо формулу
adulna)a(d
uu
=
. Інтегруючи цю рівність, одержимо
1
uuu
Caduaalnadulna
∫∫
+==
. І далі
C
a
ln
a
a
ln
C
a
ln
a
dua
u
1
u
u
+=+=
∫
. Внаслідок того, що lna величина ста-
ла то і
a
ln
C
1
- теж довільна стала, яку прийнято записувати С.
C
a
ln
a
dua
u
u
+=
∫
. (6.11)
3) Виведемо формулу інтегрування з формули
2
u1
du
darctgu
+
=
.
Одержимо
C
a
u
arctg
a
1
a
u
1
a
u
d
a
1
)
a
u
1(a
du
ua
du
2
2
2
2
2
22
+=
+
=
+
=
+
∫∫∫
.
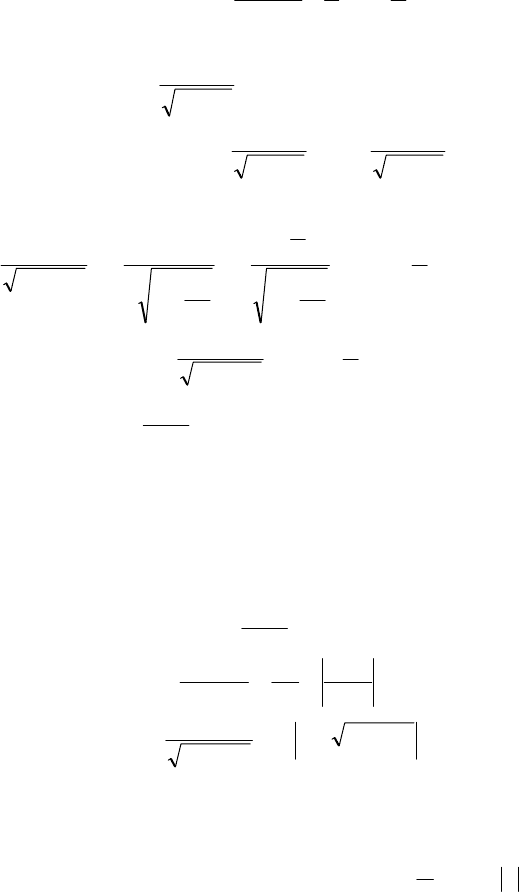
316
Отже
C
a
u
arctg
a
1
ua
du
22
+=
+
∫
(6.12)
4) Інтегруючи формулу диференціювання
2
u1
du
uarcsind
−
=
,
одержуємо
∫∫
−
=
2
u1
du
uarcsind
або
∫
+=
−
Cuarcsin
u1
du
2
. Ви-
користовуючи цю формулу, будемо мати
∫∫∫
+=
−
=
−
=
−
C
a
u
arcsin
a
u
1
a
u
d
a
u
1a
du
ua
du
2
2
2
222
.
C
a
u
arcsin
ua
du
22
+=
−
∫
. (6.13)
5)
∫
+
+
=
+
C
1n
u
duu
1n
n
,
)1n( −≠
.
Для виведення цієї формули використовують формулу для
знаходження диференціала
dunudu
1nn −
=
. Якщо показник степеня
дорівнює
n+1 формула запишеться так:
duu)1n(du
n1n
+=
+
.
Інтегруючи цю формулу (ліву і праву частину) і, зробивши перетво-
рення, одержимо
∫
+
+
=
+
C
1n
u
duu
1n
n
)1n( −≠ (6.14)
6) Формули
C
ua
ua
ln
a2
1
ua
du
22
+
−
+
=
−
∫
(6.15)
та
Cauuln
au
du
22
22
+++=
±
∫
(6.16)
доводяться диференціюванням лівої і правої частин рівності.
Такий метод доведення формул можна використовувати для
будь-якої формули інтегрування.
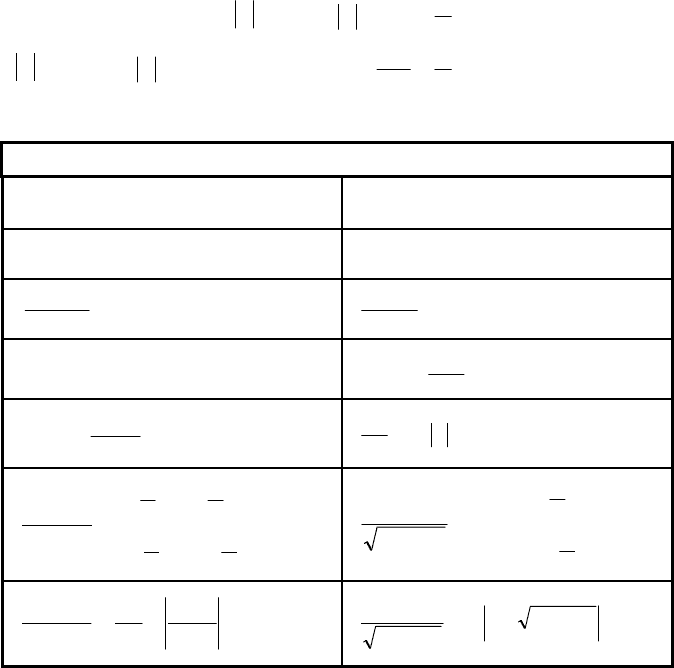
7) Доведемо справедливість формули
∫
+= Cхlndx
х
1
.
317
Нехай х>0 . Тоді xx = і
x
1
)Cx(ln =
′
+
Якщо х<0, то
xx −= і
x
1
x
1
)C)xln()Cx(ln =
−
−
=
′
+−=
′
+
. Формула доведена.
Для компактності всі формули зводять в таблицю.
1.4. Методи обчислення інтегралів
◙ Безпосереднє інтегрування
Безпосереднє інтегрування, це метод, який полягає в прямому
застосуванні табличної формули і властивостей невизначеного інте-
грала.
Приклад 1.
.Cxcosxdxsin
∫
+−=
Використали формулу
∫
+−= Cucosudusin .
Т
Т
А
А
Б
Б
Л
Л
И
И
Ц
Ц
Я
Я
О
О
С
С
Н
Н
О
О
В
В
Н
Н
И
И
Х
Х
І
І
Н
Н
Т
Т
Е
Е
Г
Г
Р
Р
А
А
Л
Л
І
І
В
В
∫∫
= dxCСdx
∫
+= Cudu
∫
+−= Cucosudusin
∫
+= Cusinuducos
Ctgu
u
os
c
du
2
+=
∫
Cctgu
u
sin
du
2
+−=
∫
∫
+= Cedue
uu
C
a
ln
a
dua
u
u
+=
∫
∫
≠α+
+α
=
+α
α
1,C
1
u
duu
1
∫
+= Culn
u
du
∫
⎪
⎩
⎪
⎨
⎧
+−
+
=
+
C
a
u
arcctg
a
1
C
a
u
arctg
a
1
au
du
22
∫
⎪
⎩
⎪
⎨
⎧
+−
+
=
−
C
a
u
arccos
C
a
u
arcsin
ua
du
22
∫
+
+
−
=
−
C
au
au
ln
a2
1
au
du
22
Cauuln
au
du
22
22
+±+=
±
∫
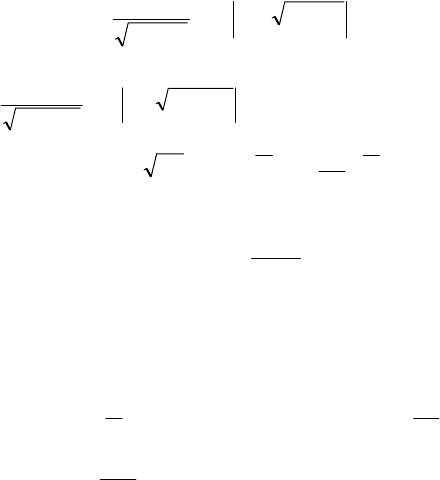
318
Приклад 2.
∫
+−+=
−
C9xxln
9x
dx
2
2
.
Для знаходження цього інтеграла використано формулу
Cauuln
au
du
22
22
+±+=
±
∫
.
Приклад 3.
∫∫
+== Cx
22
5
dxxdxxx
5
22
5
17
5
23
.
В даному випадку, після елементарних перетворень,
інтегруємо за формулою
∫
≠α+
+α
=
+α
α
1,C
1
u
duu
1
.
◙ Метод розкладу
Метод розкладу полягає в тому, що інтеграл розкладають на
суму ( різницю ) табличних інтегралів.
Приклад 4.
=+⋅−=+⋅−
∫∫∫∫
x
dx
dx25xdxcos3dx)
x
1
25xcos3(
xx
Cxln
2
ln
2
5xsin3
x
++−= .
При інтегруванні цього виразу враховано те, що сталий множ-
ник виноситься за знак інтеграла, а також те, що сума довільних
сталих інтегрування є теж стала і її записують як одну.
◙ Метод підстановки ( метод заміни змінної).
Метод полягає в тому, що вводиться нова змінна
)t(x
ϕ
= ,
або
)x(t
ψ
= . Вдалою заміною часто вдається суттєво спростити
інтеграл і навіть звести його до табличного.
Нехай
)t(x
ϕ
= - диференційована функція від t, похідна
)t(
ϕ
′
якої зберігає знак на проміжку інтегрування.
Формулу заміни змінної
∫∫
ϕ
′
ϕ= dt)t())t((fdx)x(f одержу-
ємо на основі властивості інваріантності невизначеного інтеграла
(теорема 8) і, врахувавши, що
dt)t(dx
ϕ
′
=
. Для доведення проди-
ференціюємо праву і ліву частини формули
dt)t())t((fdt)t())t((fd ϕ
′
ϕ=ϕ
′
ϕ
∫
.
dt)t())t((fdx)x(fdx)x(fd ϕ
′
ϕ==
∫
. Формула доведена.
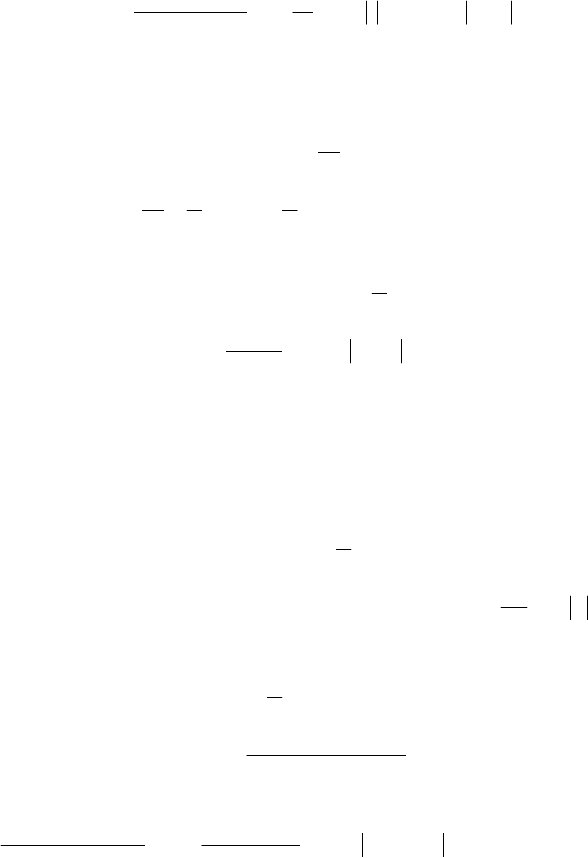
319
Приклад 5. Знайти
∫
− dx)3x(tg .
Розв’язування. При інтегруванні даного виразу вводимо замі-
ну
t=cos(x-3). Тоді dt=dcos(x-3)= -sin(x-3)dx. Одержуємо
C3xlnCtln
t
dt
)3xcos(
dx)3xsin(
dx)3x(tg +−−=+−=−=
−
−
=−
∫∫∫
.
Приклад 6. Знайти
∫
+
xdxe
3x
2
.
Розв
’язування. Вводимо заміну t3x
2
=+ . Визначаємо
xdx2dt = . Врахувавши, що
2
dt
xdx =
, одержуємо
Ce
2
1
Ce
2
1
2
dt
exdxe
3xtt3x
22
+=+==
∫∫
++
.
Розглянемо ще
дві важливі формули, які суттєво пришвид-
шують інтегрування:
∫
++=+ C)bax(F
a
1
dx)bax(f
(6.17)
та
∫
+=
′
C)x(ulndx
)x(u
)x(u
. (6.18)
Виведемо їх. Якщо
C)u(Fdu)u(f +=
∫
і baxu += -
лінійна функція від
х, то adx)bax(ddu =+= . Підставивши в вираз
для інтеграла, одержимо
C)bax(Fdx)bax(fa)bax(d)bax(f ++=+=++
∫∫
.
З останньої рівності випливає, що
∫
++=+ C)bax(F
a
1
dx)bax(f
.
Друга формула виводиться на основі формули
∫
+= Culn
u
du
з врахуванням того, що
du)x(u)x(du
′
= .
Приклад 7.
∫
+=
−−
Ce
5
1
dxe
6x56x5
,
Приклад 8. Знайти
∫
++
dx
)8xln()8х(
1
.
Розв
’язування.
∫∫
++=
+
′
+
=
++
C)8xln(lndx
)8xln(
))8x(ln(
dx
)8xln()8
х(
1
.
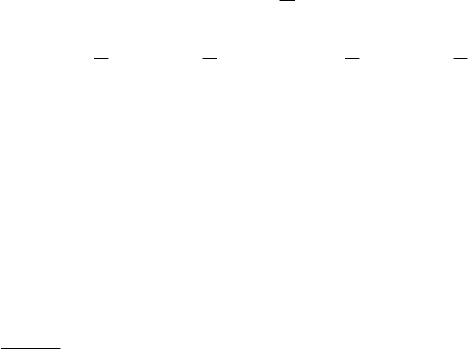
320
◙ Метод інтегрування частинами
Нехай задано дві неперервно диференційовані функції u(x) i
v(x). Розглянемо диференціал добутку: .vduudv)vu(d +=⋅
Проінтегруємо цей вираз
∫∫∫
+=⋅ vduudv)vu(d . Перетворивши
одержуємо формулу інтегрування за частинами:
∫∫
−= vduuvudv
. (6.19)
Застосовуючи цю формулу, підінтегральний вираз
dx)x(f
подають у вигляді добутку множників
u
і dv . Для даного методу
має велике значення правильний вибір функцій
u і v. Необхідно,
щоб множник
dv
був виразом, який інтегрується. Є декілька видів
інтегралів, для яких правила вибору функцій
u і v відомі.
а)
∫
α
dxe)x(P
x
n
,
∫
α dx)xsin()x(P
n
,
∫
α dx)xcos()x(P
n
.
Підінтегральний вираз містить добуток многочлена на триго-
нометричну, або многочлена на показникову функції. Вибираємо за
u
многочлен, а за dv - вираз, що залишився.
Приклад 9. Обчислити
∫
xdx3sinx
.
Розв’язування. Застосовуємо метод інтегрування за частинами
(6.19):
∫∫
−= vduuvudv
. Вибираємо: u=x, dv=sin3xdx.
Тоді du=dx, v=
3
1
xdx3sin −=
∫
cos3x. Одержуємо
∫∫
++−=+−= Cx3sin
9
1
x3cosx
3
1
xdx3cos
3
1
x3cosx
3
1
xdx3sinx
.
б)
∫
xdxln)x(P
n
,
∫
xdxarcsin)x(P
n
,
∫
xdxarccos)x(P
n
,
∫
arctgxdx
)x(P
n
,
∫
arcctgxdx)x(P
n
.
Підінтегральний вираз - добуток многочлена на логарифмічну
або многочлена на аркфункцію. За
dv беремо добуток многочлена
на
dx, а за u логарифмічну або аркфункцію.
Приклад 10. Обчислити
xdxarctg
∫
Розв
'язування. За u беремо
arctgx
, за dv - dx. Тоді
2
x1
dx
du
+
=
, а v=x, і за формулою інтегрування за частинами
