Сербо В.Г., Хриплович И.Б. Конспект лекций по квантовой механике
Подождите немного. Документ загружается.

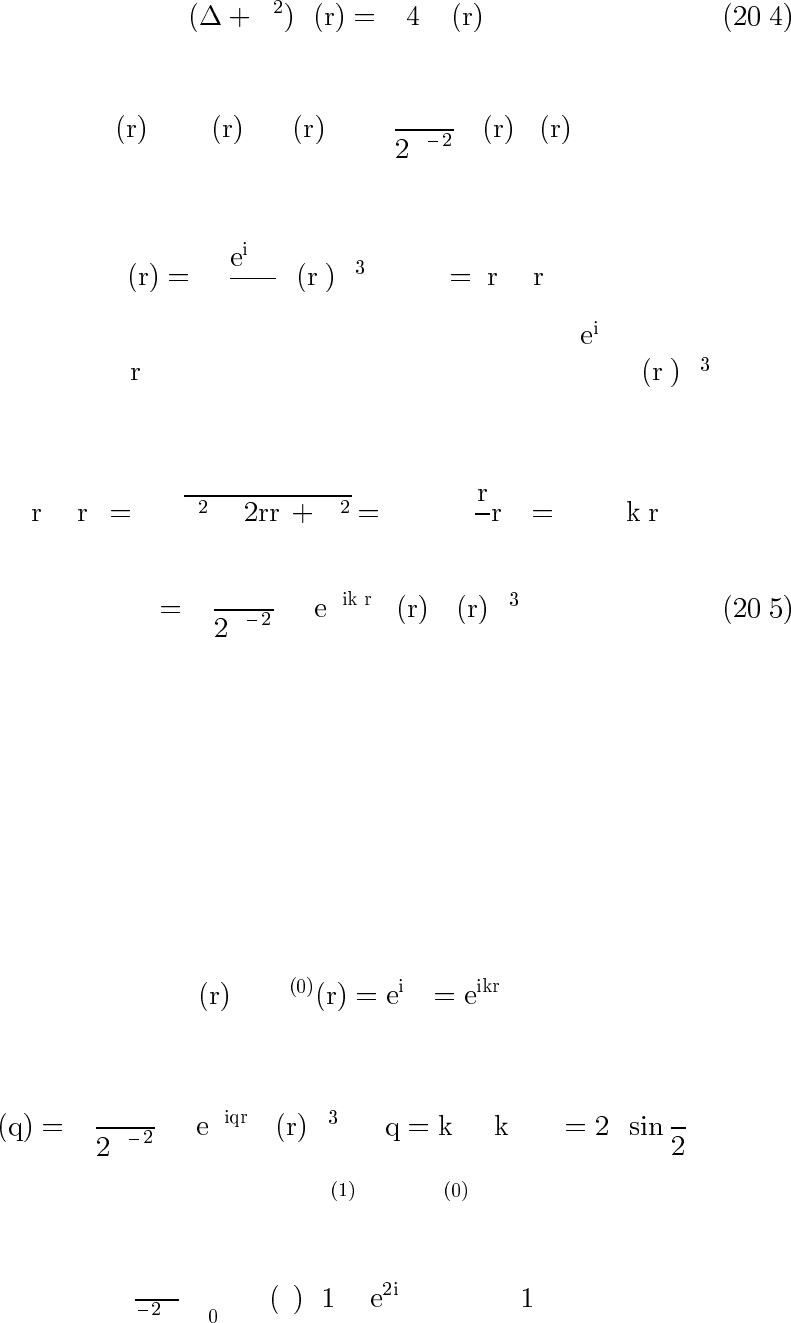
имеет вид
k ϕ − πρ , .
аналогичный (20.1) с заменой
ϕ
→ ψ ,ρ →−
m
πh
U ψ .
Решение же уравнения (20.4) в форме запаздывающих потенциалов
таково:
ϕ
Z
kR
R
ρ
0
d r
0
,R |−
0
|,
что соответствует суперпозиции сферических волн
kR
/R,расходя-
щихся из центров
0
, в которых состредоточены заряды ρ
0
d r
0
.
При r a соотношение (20.3) приводится к виду (20.2). Дей-
с тв ител ьн о , п ри этом
k |
−
0
| k
√
r −
0
r
0
k
r −
r
0
!
kr −
0 0
,
так что
f
−
m
πh
Z
−
0
ψ U d r. .
§21. Борновское приближение.
Формула Резерфорда. Атомный формфактор
Борновское приближение
Рассматриваем потенциал как возмущение. Для получения ампли-
туды рассеяния в первом порядке по потенциалу взаимодействия,
подставим в (20.5) невозмущенную волновую функцию
ψ
≈ ψ
kz
иполучим
f
−
m
πh
Z
−
U d r,
0
− ,q k
θ
.
Критерий применимости: |ψ
||ψ |, что дает для сфериче-
ски симметричного потенциала условие
m
h k
Z
∞
U r
−
kr
dr
.
61
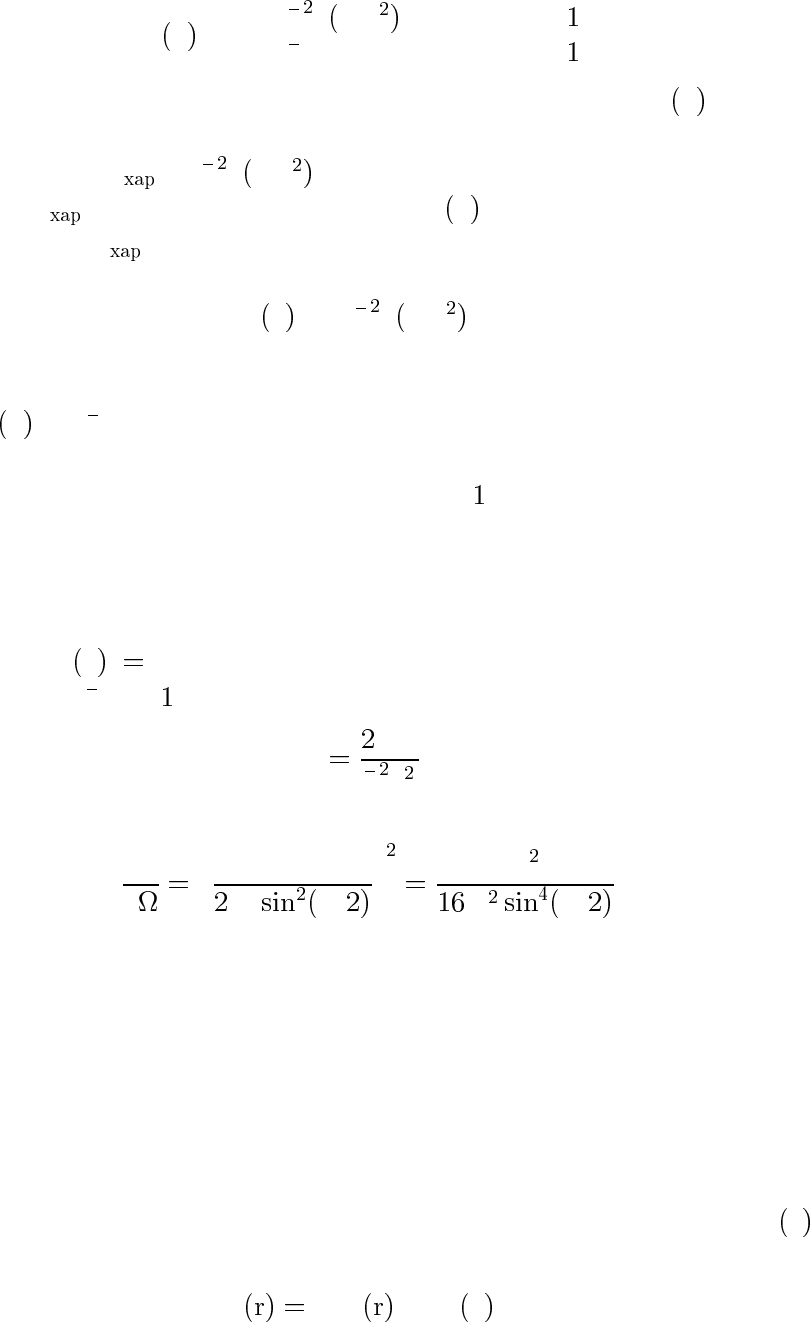
Оно приводится к
|U
a |
h/ma при ka ,
hv/a при ka .
Иными словами, характерная потенциальная энергия |U
a | должна
быть мала либо (для медленных частиц) по сравнению с характер-
ной энергией E
∼ h / ma , либо (для быстрых частиц) по срав-
нению с E
·ka (в последнем случае |U a |может быть и не мала по
сравнению с E
).
Критерий применимости борновского приближения для рассея-
ния медленных частиц |U
a |h/ma соответствует тому, что в
случае притягивающего потенциала притяжение недостаточно для
образования связанного состояния. В случае быстрых частиц усло-
вие |U
a |hv/a соответствует тому, что неопределенность в энер-
гии, связанная с временем пролета, должна быть много больше по-
тенциала взаимодействия; условие ka
о бесп ечи вает зд есь п ри -
менимость квазиклассического рассмотрения.
Формула Резерфорда
Для поля U
r −α/r критерий применимости борновского при-
ближения α/
hv . Борновская амплитуда равна
f
αm
h q
,
а сечение рассеяния
dσ
d
α
pv θ/
α
E θ/
совпадает с классическим. Отметим без доказательства, что бор-
новская формула для сечения совпадает с точной (это верно лишь в
нерелятивистском приближении). Полное сечение равно бесконеч-
ности.
Атомный формфактор
При упругом рассеянии быстрых электронов на атоме последний
можно рассматривать как источник статического потенциала ϕ
r ,
создаваемого средним распределением зарядов в атоме
ρ
Zeδ − en r .
62
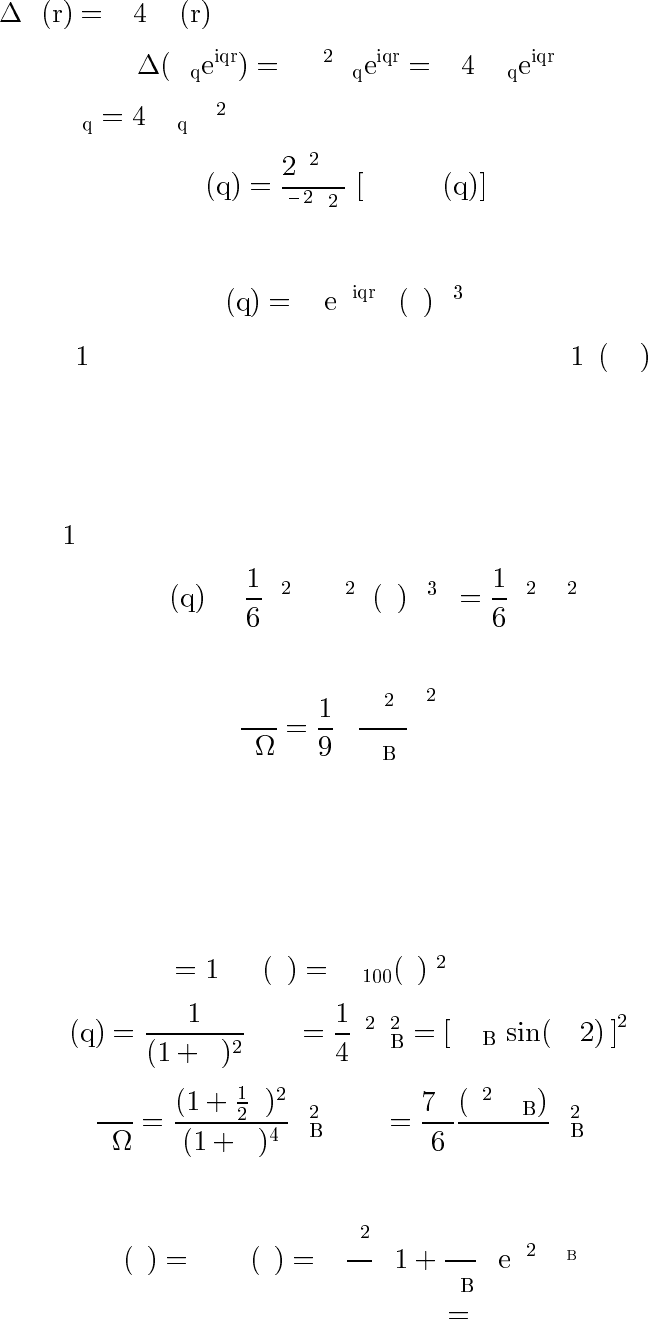
Та к как ϕ − πρ ,тоиз
ϕ −q ϕ − πρ
следует , что ϕ πρ /q . Таким образом,
f
e m
h q
Z − F .
Здесь введен так называемый атомный формфактор:
F
Z
−
n r d r.
При qa
, то есть при углах рассеяния θ / ka ,формфак-
то р |F|Zи сечение совпадает с резерфордовским. Это вполне
естественно: большие углы рассеяния соответствуют малым при-
цельным параметрам, при которых налетающая частица рассеива-
ется ядром, практически неэкранированным.
При qa
имеем
Z −F
≈ q
Z
r n r d r q hr i.
В этой области дифференциальное сечение
dσ
d
hr i
a
.
Таким образом, при рассеянии на атоме полное сечение оказывается
(в отличие от резерфордовского) конечным.
Пример
Атом водорода. Z
,nr |ψr | , п оэтом у
F
u
,u qa ka θ/ ,
dσ
d
u
u
a ,σ
πe/a
E
a
.
Указанному распределению зарядов соотвествует потенциальная энер-
гия
U
r −eϕ r −
e
r
r
a
!
−r/a
.
В классической механике в таком поле σ
∞, что находится в рез-
ком противоречии с квантовым (правильным!) результатом.
63
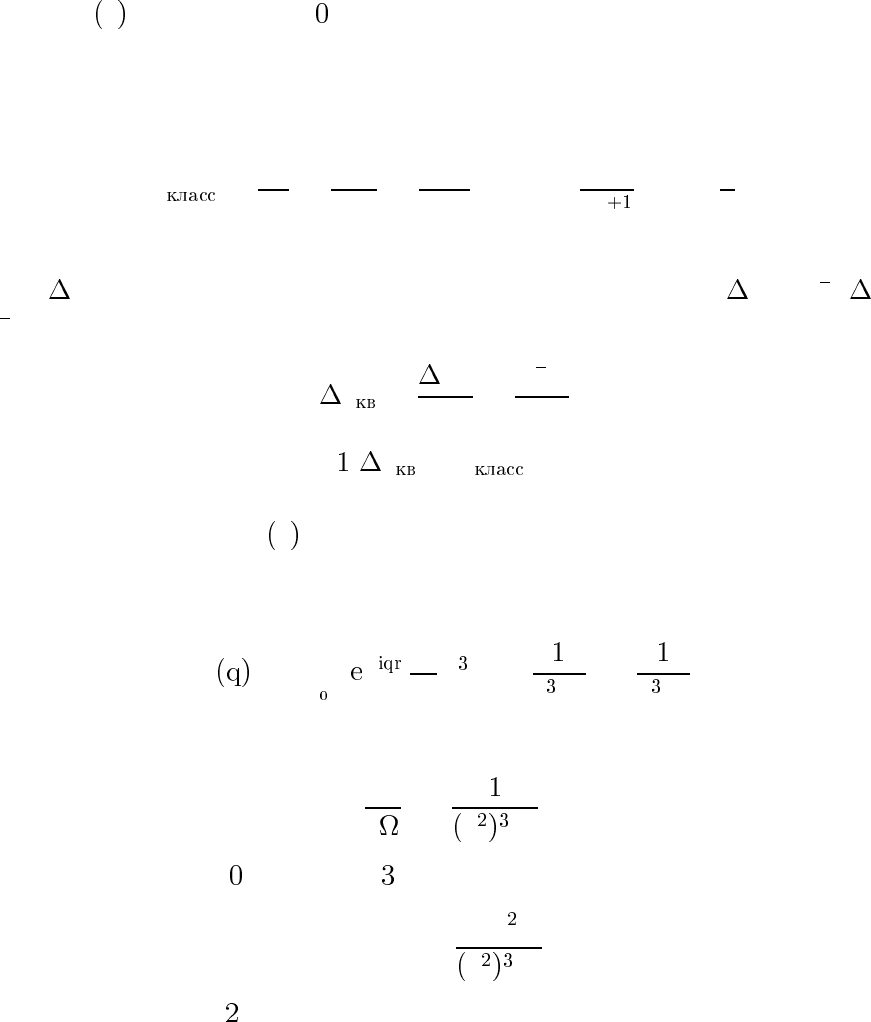
Конечные сечения в квантовой механике
Обсудим подробнее вопрос о том, какие потенциалы приводят в кван-
товой механике к конечным сечениям. Пусть на больших расстоя-
ниях U
r ∼ α/r
n
, n> . В классической механике при рассеянии
в таком поле полное сечение бесконечно, так как любым большим
прицельным параметрам ρ соответствуют хотя и малые, но конеч-
ные классические углы отклонения
θ
∼
p
⊥
p
z
∼
F
⊥
t
mv
∼
α
ρ
n
E
,F
⊥
∼
α
ρ
n
,t∼
ρ
v
.
В квантовой механике для частицы с прицельным параметром ρ (у
нее
r
⊥
<ρ) неопределенность поперечного импульса p
⊥
>
∼ h/ r
⊥
>
h/ρ, поэтому квантовая неопределенность угла отклонения равна
θ ∼
p
⊥
p
z
>
h
ρmv
.
Та ки м об ра з ом, при n>
θ >θ и поэтому кв ан том ехан ич е-
ские результаты могут существенно отличаться от классических.
Зная поведение U
r на больших расстояниях, где взаимодействие
всегда слабое и поэтому борновское приближение применимо, мож-
но оценить поведение амплитуды в области малых углов рассеяния:
f
∝
Z
∞
r
−
α
r
n
d r ∝
q
−n
∝
θ
−n
.
Отсюда получаем, что дифференциальное сечение
dσ
d
∝
θ
−n
конечно при θ → ,еслиn> , а полное сечение
σ ∝
Z
dθ
θ
−n
конечно при n> .
Опыты по рассеянию быстрых электронов на ядрах. Формфакто-
ры элементарных частиц.
ВОПРОСЫ
64
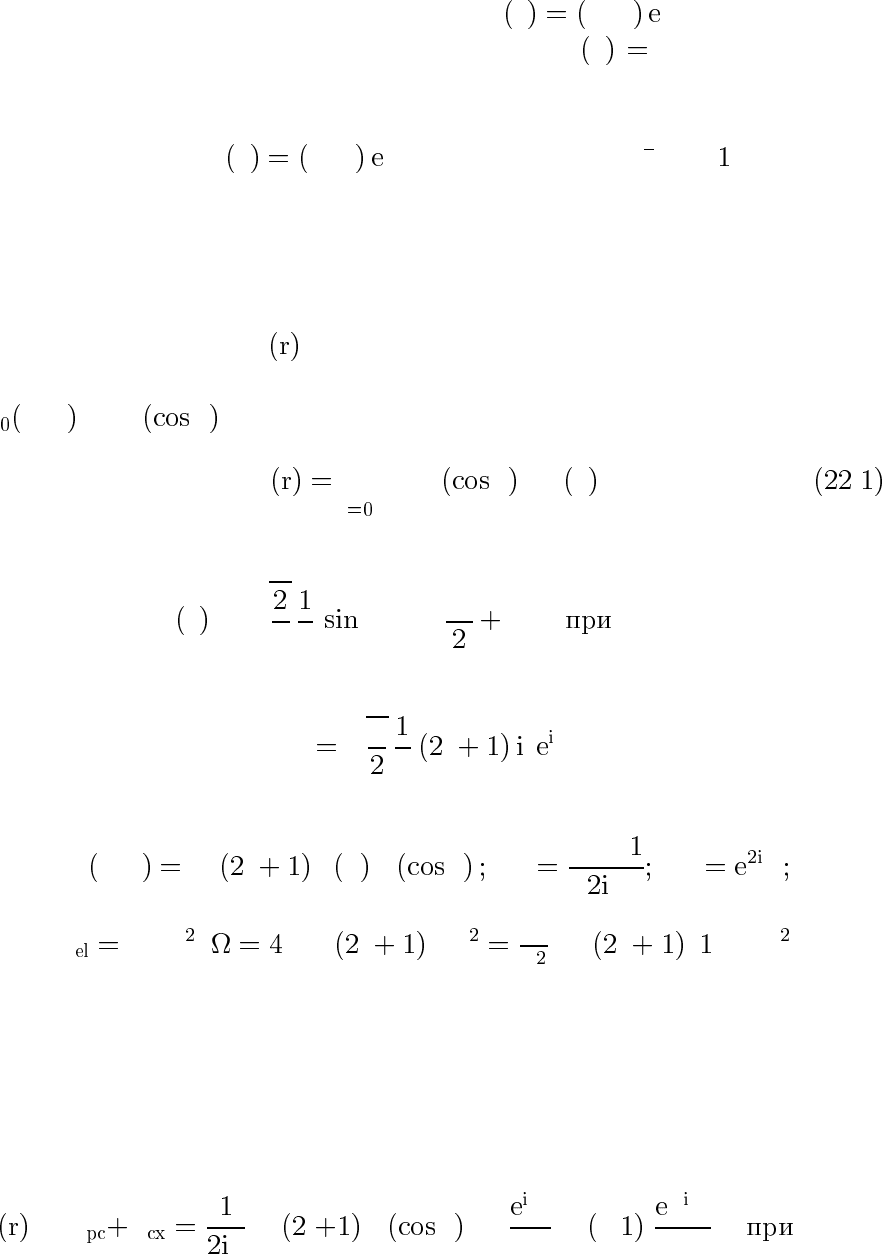
21.1. Рассеяние на прямоугольной потенциальной яме в борнов-
ском приближении (задача 1 к § 126 КМ). Обсудить условия приме-
нимости приближения.
21.2. То же для потенциала Юкава U
r α/r
−r/a
.
21.3. То же для кулонового потенциала U
r α/r (предельный
случай потенциала Юкава при a →∞).
21.4. Найти полное сечение рассеяния быстрой частицы на по-
тенциале Юкава U
r α/r
−r/a
при условии α/hv .
22. Фазовая теория рассеяния
Рассеяние на сферически симметричном потенциале является сим-
метричным, то есть ψ
зависит лишь от r и θ,нонеотϕ. Поэтому
разложение этого решения по парциальным волнам содержит лишь
Y
l
θ, ϕ ∝ P
l
θ :
ψ
∞
X
l
A
l
P
l
θ R
kl
r . .
Как известно (см. §15),
R
kl
r →
v
u
u
t
π r
kr −
πl
δ
l
!
r →∞.
Чтобы выполнялось граничное условие (20.2), необходимо
A
l
s
π
k
l
lδ
l
.
Тогд а
f
k, θ
X
l
l f
l
kP
l
θ f
l
S
l
−
k
S
l
δ
l
σ
Z
|f| d π
X
l
l |f
l
|
π
k
X
l
l |−S
l
|.
Понятие о неупругом сечении
Решение (22.1) при r →∞можно представить не только в виде
(20.2), но и в виде двух сферических волн, расходящейся и сходя-
щейся:
ψ
→ψ ψ
k
X
l
l P
l
θ
S
l
kr
r
−
−
l
− kr
r
r →∞
65
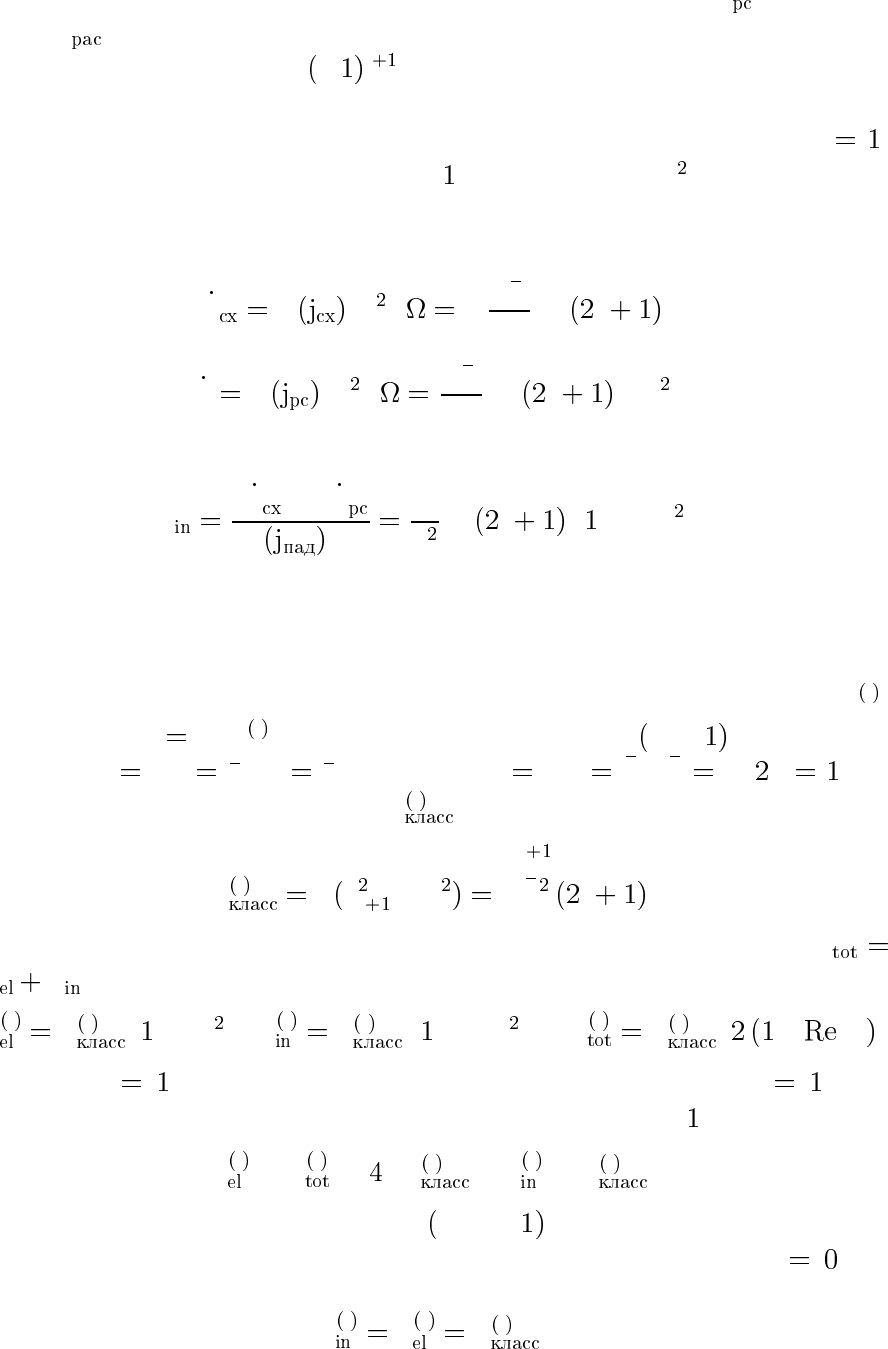
(разумеется, при таком разбиении расходящаяся волна ψ отличает-
ся от ψ
в (20.2)). Парциальная амплитуда расходящейся волны от-
личается на множитель
−
l
S
l
от соответствующей амплитуды в
сходящейся волне. Если нет поглощения частиц силовым центром,
то этот множитель должен быть по модулю равен единице, |S
l
| .
Если есть поглощение, то |S
l
| < , а величина |S
l
| характеризует
уменьшение потока частиц в расходящейся волне по сравнению с
потоком частиц в сходящейся. Действительно,
N
Z
r
r d −
π
h
mk
X
l
l ,
N
Z
r
r d
πh
mk
X
l
l |S
l
|.
Поэтому неупругое сечение равно
σ
|N |−N
z
π
k
X
l
l
−|S
l
|
.
Оптическая теорема
Для процессов рассеяния и поглощения существуют определенные
ограничения и связи. Введем понятие парционального сечения σ
l
,
представив σ
P
l
σ
l
. В классической механике l момент им-
пульса M
pρ
l
hkρ
l
hl, п оэтом у ρ
l
l/k λl (λ λ/ π /k),
а под парциальным сечением σ
l
естественно понимать площадь
кольца между окружностями радиусов ρ
l
и ρ
l
,тоесть
σ
l
π ρ
l
− ρ
l
π λ l .
Парциальные сечения для упругого, неупругого и полного σ
σ σ сечения можно записать в виде
σ
l
σ
l
| −S
l
| ,σ
l
σ
l
−|S
l
|
,σ
l
σ
l
· −S
l
.
При S
l
нет ни поглощения, ни рассеяния; при |S
l
| ес ть
только рассеяние, но нет поглощения. Так как |S
l
|≤ ,то
σ
l
≤ σ
l
≤ · σ
l
,σ
l
≤ σ
l
.
Если есть поглощение частиц
|S
l
| < , то непременно происхо-
дит и рассеяние частиц. Поглощение максимально при S
l
ив
этом с луч ае
σ
l
σ
l
σ
l
.
66
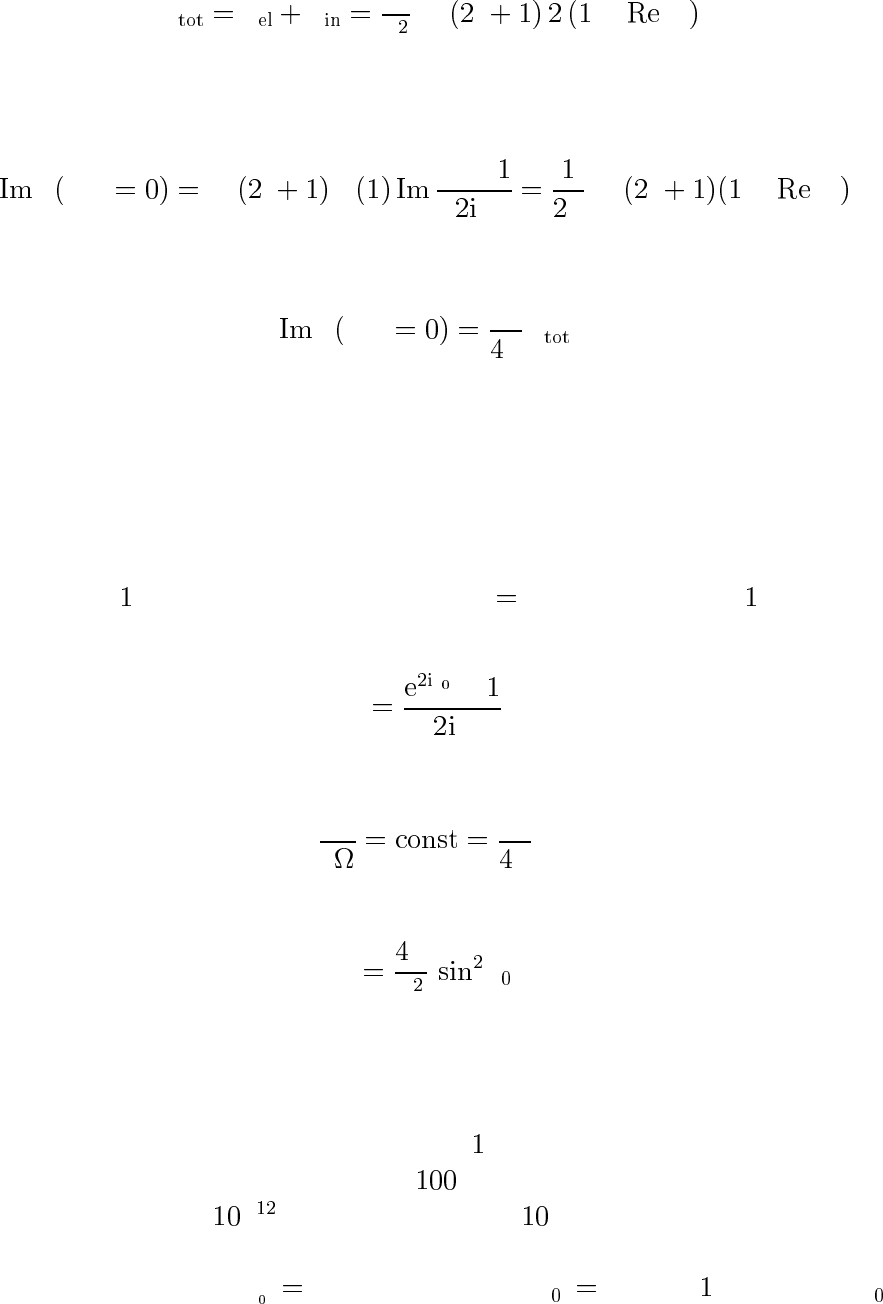
Еще одно соотношение возникает, если сравнить
σ
σ σ
π
k
X
l
l −S
l
с выражением для мнимой частицы амплитуды рассеяния на угол
нуль:
f k, θ
X
l
l P
l
S
l
−
k k
X
l
l − S
l
.
Отсюда получаем оптическую теорему:
f k, θ
k
π
σ
.
Ее смысл тот же, что и в оптике: ослабление падающего потока
происходит за счет интерференции падающей волны и волны, рас-
сеянной под очень малыми углами.
Упругое рассеяние медленных частиц
При ka
прицельные параметры ρ
l
l/k a для l ≥ , п оэтом у
лишь s-волна может давать заметное рассеяние. Таким образом,
f
δ
−
k
,
дифференциальное сечение изотропно
dσ
d
σ
π
,
а полное сечение определяется фазой s-волны
σ
π
k
δ .
Дифракционное рассеяние быстрых частиц на черном шаре
Пусть идеально поглощающий (черный) шар имеет радиус a. Рас-
смотрим рассеяние быстрых (ka
) частиц на таком шаре (при-
мер: нейтроны с энергией E ∼
МэВ рассеиваются на тяжелом
ядре радиуса a ∼
−
с м, пр и этом ka ∼ ). Эта задача вполне ана-
логична дифракции плоской световой волны на черном шаре. При-
цельный параметр ρ
l
a соответствует l ka .Приl>l
67
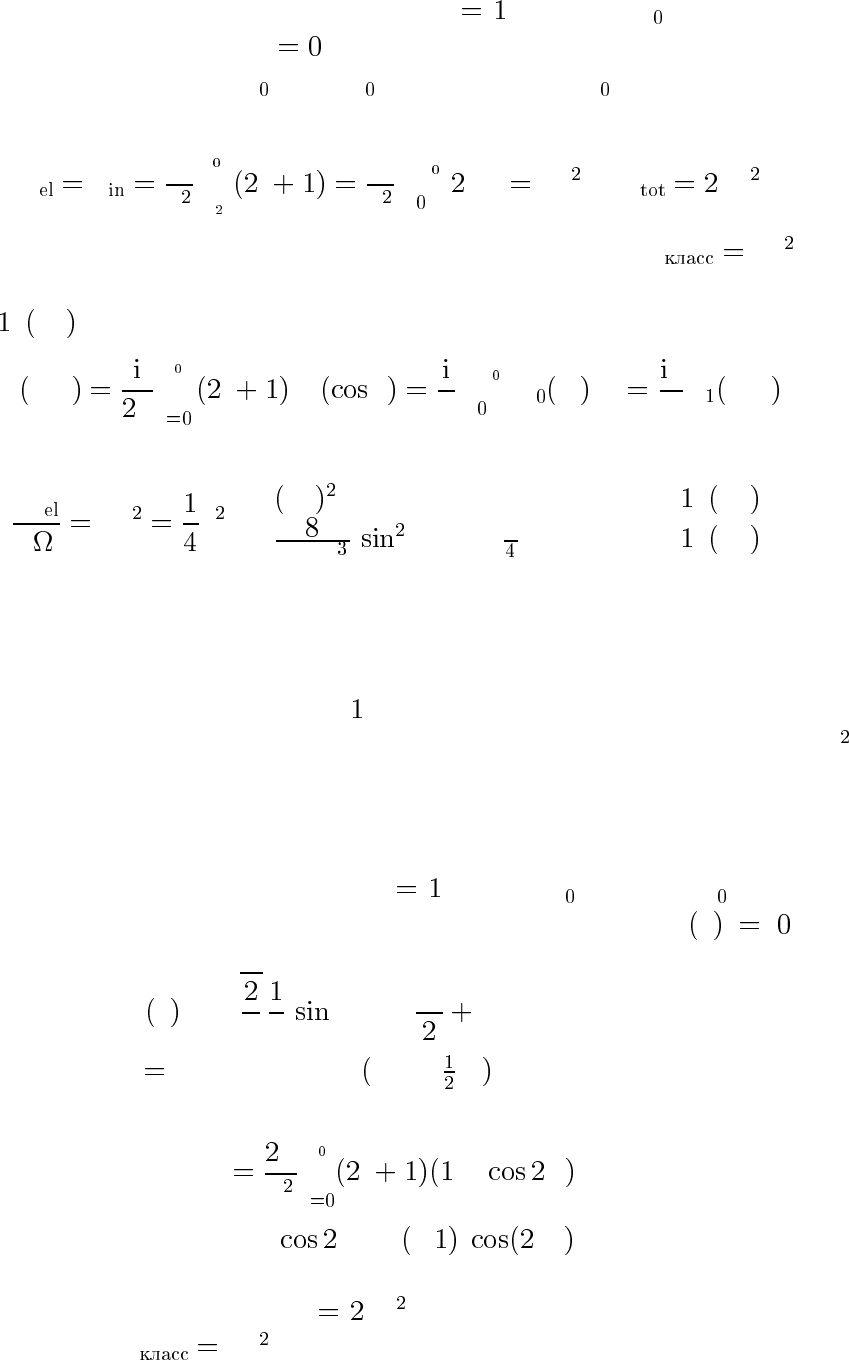
частицы не сталкиваются с шаром, S
l
.Приl<l частицы пол-
ностью поглощаются, S
l
. Строго говоря, эти утверждения спра-
ведливы лишь для l l
и l l , но область l ≈ l не дает большого
вклада в сечение. Таким образом,
σ
σ
π
k
l
X
k
l
π
k
Z
l
ldl πa ,σ πa ,
то есть полное сечение вдвое больше классического σ
πa .
Амплитуда упругого рассеяния велика лишь в области малых углов
θ
<
∼ / ka :
f
k, θ
k
l
X
l
l P
l
θ
k
Z
l
lJ lθ dl
a
θ
J
kaθ .
По этом у
dσ
d
|f| a ·
ka при θ / ka
πkaθ
kaθ −
π
при θ / ka .
Упругое рассеяние быстрых частиц на идеально отражающем
шаре
Пусть радиус шара a и ka
. Полное сечение определяет число
частиц, выбывших из начального пучка. В классике это сечение πa
связано лишь с прямым столкновением с мишенью. С учетом вол-
новых свойств частиц их выбывание из пучка, то есть изменение
начального импульса, связано также с дифракцией.
Как и в предыдущем случае S
l
при l>l.Приl<l решение
УШ для радиальной волновой функции имеет вид R
kl
r при
r<aи
R
kl
r ≈
v
u
u
t
π r
kr −
πl
δ
l
!
при r>a.
Сшивка при r
a дает δ
l
≈−ka − πl . Для нахождения полного
сечения используем оптическую теорему
σ
π
k
l
X
l
l − δ
l
.
Слагаемые, содержащие
δ
l
≈ −
l
ka , быстро осциллиру-
ют при изменении l, и поэтому их вкладом в сумму можно прене-
бречь. В итоге получаем σ
πa , что вдвое превышает классиче-
ское сече ни е σ
πa .
68
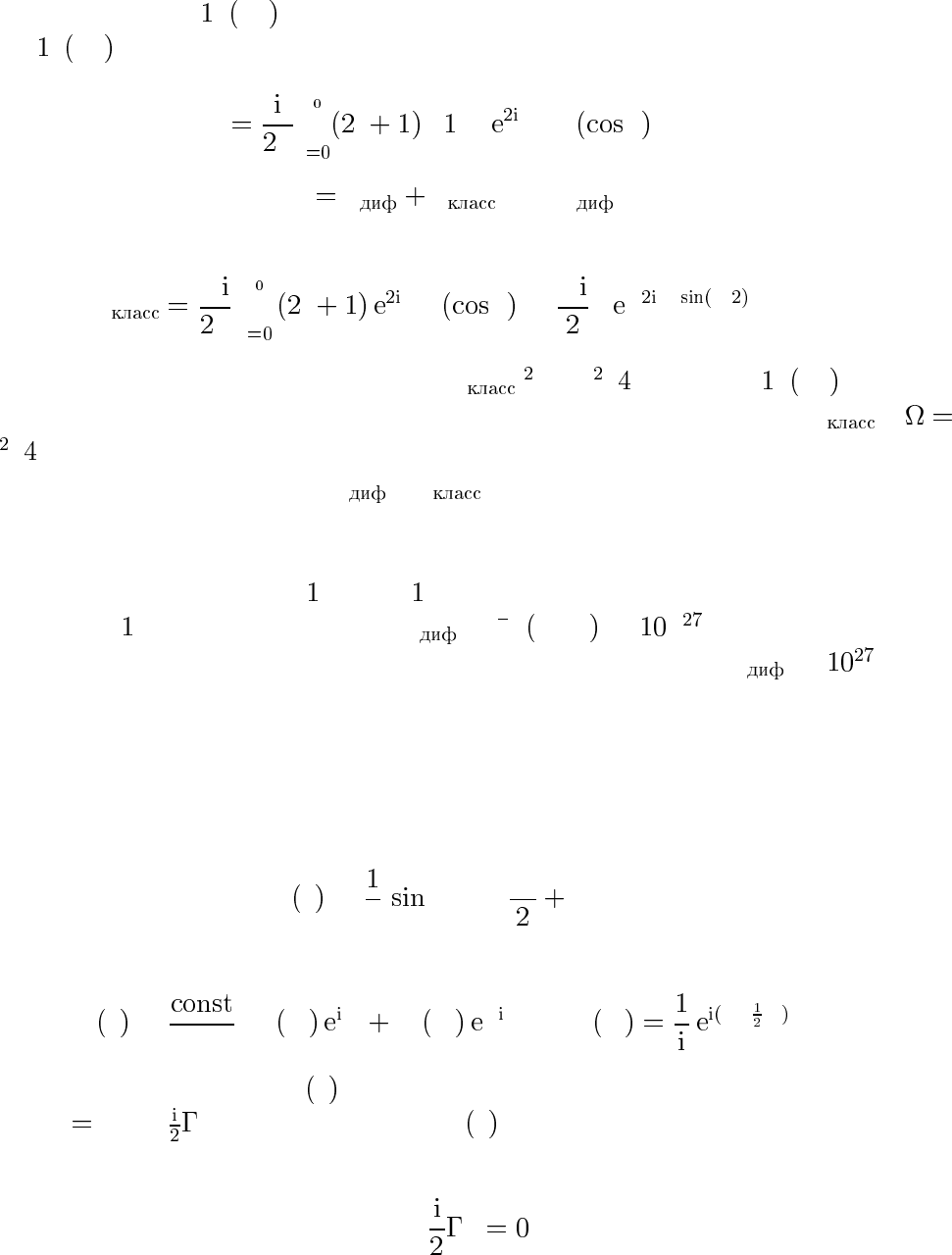
В данном случае отличие от классического результата связано
с наличием помимо квазиклассического рассеяния, обусловленно-
го углами θ
/ ka , дифракционного рассеяния на малые углы
θ
<
∼ / ka . Чтобы увидеть это, представим амплитуду рассеяния
f
k
l
X
l
l
−
δ
l
P
l
θ
в виде двух слагаемых f f f ,гдеf совпадает с ампли-
тудой рассеяния в предыдущем случае, а
f
−
k
l
X
l
l
δ
l
P
l
θ ≈
−
a
− ka θ/
.
Доказательство того факта, что |f
| ≈ a / при θ / ka (в
полном соответствии с классическим изотропным рассеянием dσ
/d
a/) можно найти в задаче 13.32 ГКК.
Таким образом, вклады f
и f в полное сечение одинаковы,
а вклад их интерференции пренебрежимо мал.
Для классических частиц дифракция практически ненаблюдаема.
Так, для частицы с m ∼
г, v ∼ см/с углы дифракции на шаре ра-
диуса a ∼
см настолько малы, θ ∼ h/ mva ∼
−
, что увидеть
это рассеяние можно было бы лишь на расстояниях ∼ a/θ
∼
см.
Резонансное рассеяние
Перепишем асимптотическое выражение (при r →∞)
R
kl
r ∝
r
kr −
πl
δ
l
!
в виде
R
kl
r →
r
h
a
l
E
kr
a
∗
l
E
−kr
i
,a
l
E
δ
l
− πl
.
Если в данном поле U
r возможно квазистационарное состояние
при E
E
r
− , то асимптотика R
kl
r при данной энергии должна
сод е ржа т ь тол ь ко р а схо д ящу юс я вол н у, то ес т ь
a
∗
l
E
r
−
!
.
69
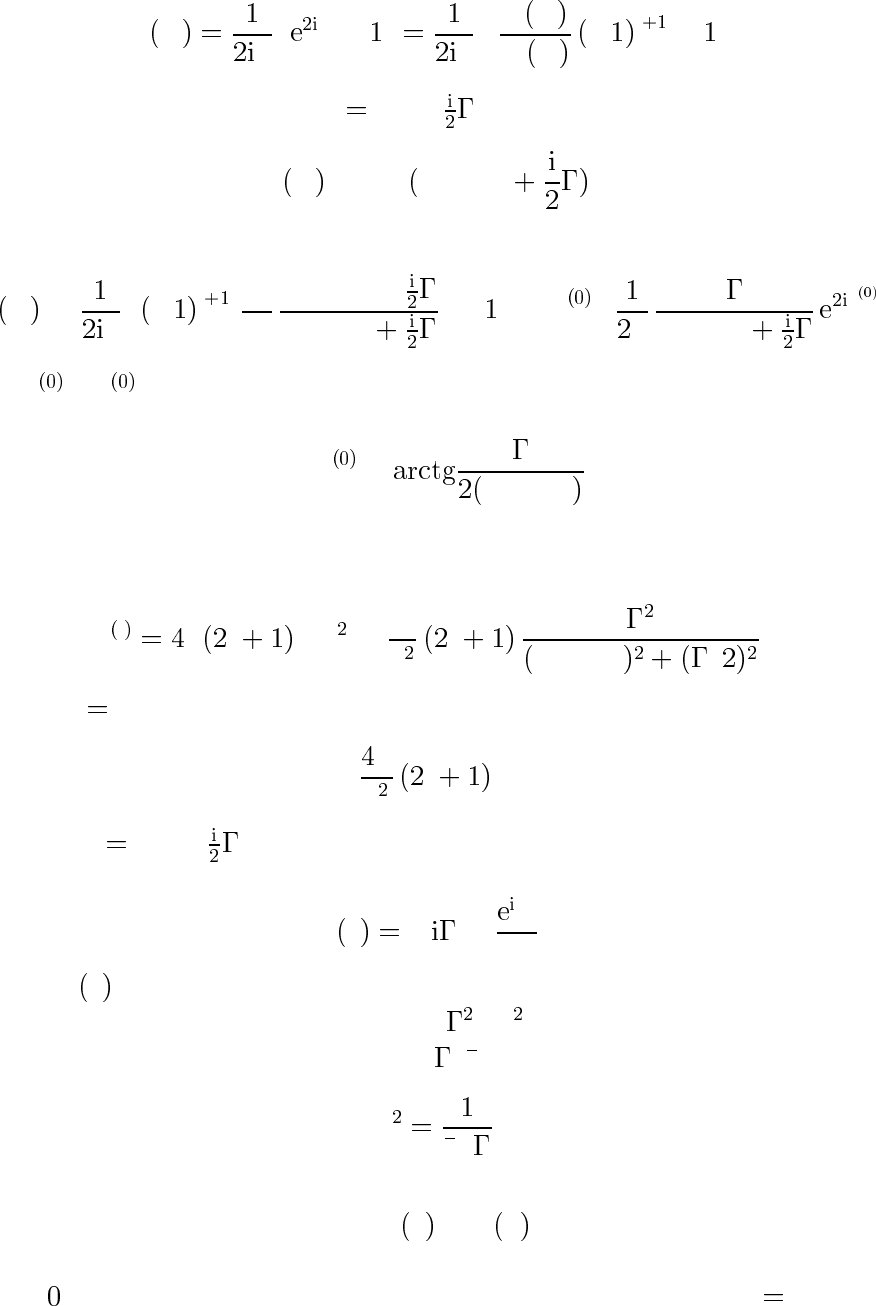
Отсюда следует, что парциальная амплитуда рассеяния
f
l
E
k
δ
l
−
k
a
l
E
a
∗
l
E
−
l
−
должна иметь полюс при E E
r
− . Пусть вблизи резонанса
a
∗
l
E ≈ β
l
· E −E
r
,
то гд а
f
l
E ≈
k
−
l
β
∗
l
β
l
E − E
r
−
E − E
r
−
≈ f
l
−
k
E − E
r
δ
l
,
где δ
l
и f
l
— фаза и амплитуда рассеяния вдали от резонанса, при-
чем
δ
l
≈ δ
l
−
E −E
r
.
При прохождении через резонанс фаза рассеяния изменяется на π.
Парциальное сечение имеет резонансную зависимость от энергии:
σ
l
π l |f
l
|→
π
k
l
E−E
r
/
иприE E
r
достигает максимально возможного значения
π
k
l .
При E
E
r
− радиальная волновая функция на больших рас-
стояниях равна
R
l
r −β
∗
l
kr
r
.
Если R
l
r нормирована во внутренней области на единицу, то пол-
ный поток в расходящейся волне v
|β
l
| должен равняться вероят-
ности распада в единицу времени
/h. Отсюда
|β
l
|
hv
.
Аналогичным образом можно показать, что при аналитическом
продолжении по k функций R
kl
r и f
l
k в область отрицательных
значений E (при этом k → iκ), связанным состоянием с энергией
E
n
< соответствуют полюса амплитуды рассеяния при E E
n
.
70
