Сербо В.Г., Хриплович И.Б. Конспект лекций по квантовой механике
Подождите немного. Документ загружается.


ВОПРОСЫ
22.1. Вычислить сечение рассеяния медленных частиц в поле
U
r −Gδ r −a в условиях резонанса в s-волне (задача 13.34
ГКК).
22.2. Найти сечение рассеяния медленных частиц в случае:
а) сферической прямоугольной потенциальной ямы (включая и
резонансное рассеяние — см. задачу 13.35 ГКК);
б) сферического прямоугольного потенциального барьера.
22.3. Найти фазовые сдвиги δ
l
k вполеU r α/r , α> .Вы-
полнить суммирование ряда, представляющего разложение ампли-
туды по парциальным волнам, в случае mα/
h при произволь-
ных углах рассеяния. Найти dσ/d
и σ ( задача 13.29а ГКК). Срав-
нить с классическим рассеянием на малые углы.
22.4. Как ведет себя сечение неупругого рассеяния в пределе ма-
лых скоростей?
§23. Гайзенберговское представление
В обычном (шредингеровском) представлении операторы и
− h∇ не зависят от t, а оператор физической величины A , ,t мо-
жет за ви сеть о т t лишь частным образом. Зависимость среднего зна-
чения этой величины от времени
hA
t i
Z
∗
,t A ,t d r h t |A | t i,
связана в основном с волновой функцией
,t , которая удовлетво-
ряет УШ
h
∂
∂t
,t H,t .
Представим волновую функцию в виде
,t
X
n
a
n
−E
n
t/h
ψ
n
U t , U t
−Ht/h
или
|
t i U t | i.
Тогда среднее значение hA
t i можно записать так:
hA
t i h |A
H
t | i,
71

где
A
H
t U
−
tAUt
— это оператор в гайзенберговском представлении. Таким образом,
зависимость от времени в гайзенберговском представлении перене-
сена с волновых функций на операторы. При этом
H
H
U
−
HU H.
Легко получить выражение для производной по времени от опе-
ратора в гайзенберговском представлении:
d
A
H
dt h
h
H,A
H
i
∂A
H
∂t
.
ВОПРОСЫ
23.1. Задачи 7.29-7.31 ГКК. Найти операторы координаты и им-
пульса в гайзенберговском представлении для линейного гармони-
ческого осциллятора.
Задачу предлагается решить двумя способами:
а) используя унитарное преобразование, связывающее операто-
ры физических величин в гайзенберговском и шредингеровском пред-
ставлениях;
б) непосредственным решением уравнений движения для гайзен-
берговских операторов.
23.2. Задачи 7.34 ГКК. Найти значение “разновременного” ком-
мутатора импульса и координаты
pt,xt
0
для: а) свободной ча-
стицы; б) частицы в однородном поле; в) линейного осциллятора.
23.3. Задача 7.36 ГКК. Используя вид гайзенберговских операто-
ров
p t , x t , найти зависимость от времени следующих средних:
hx
t i, hp t i, h x t i, h p t i
для линейного осциллятора в состоянии, описываемом волновой функ-
цией вида
ψ
x A
ip x
h
−
x − x
a
.
72
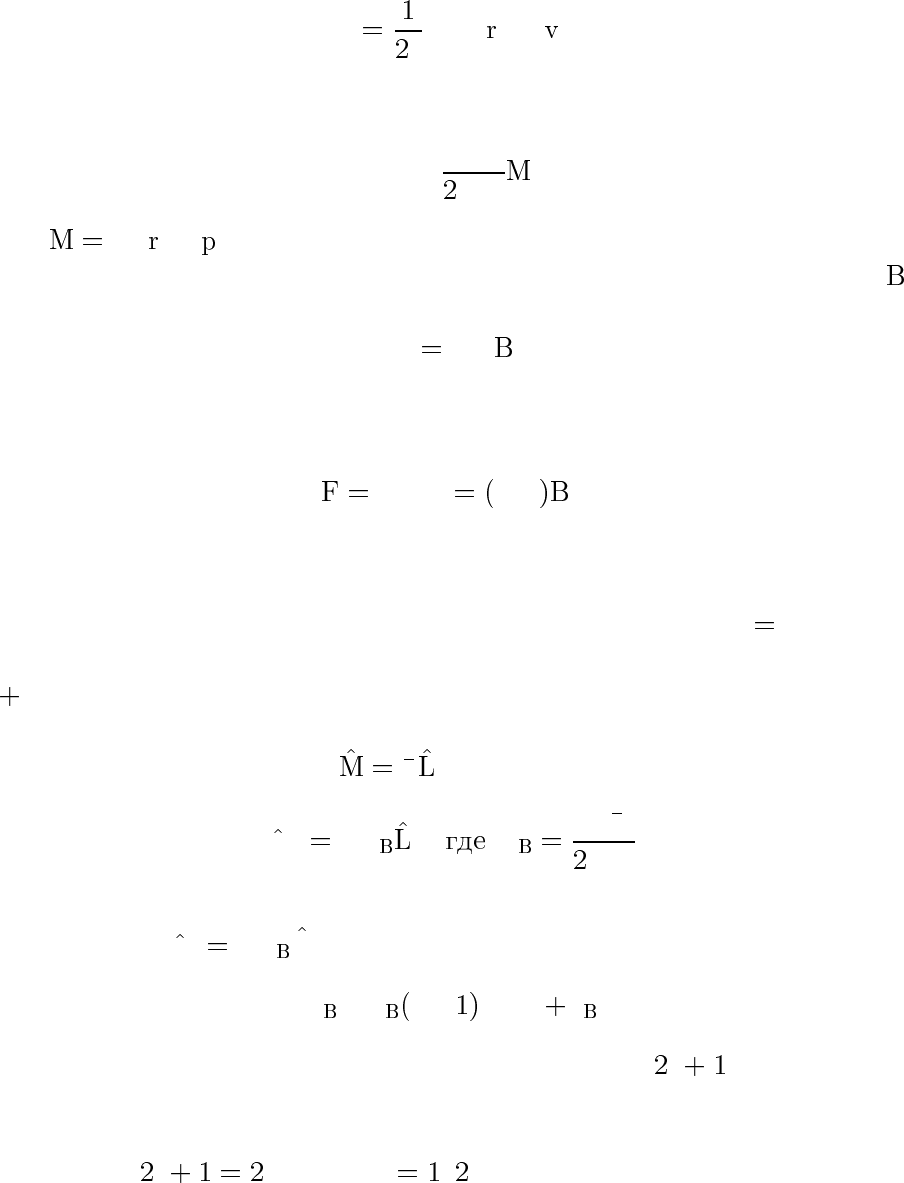
§24. Опыт Штерна–Герлаха. Спин
В классической теории магнитный момент атома
µ
c
X
a
e
a a
×
a
обусловлен в основном движением электронов
µ ≈−
|e|
m
e
c
,
где
P
e
e
×
e
– орбитальный момент импульса электронов. Вза-
имодействие нейтрального атома со внешним магнитным полем
описывается добавкой
V
−µ
к функции Гамильтона. Во внешнем неоднородном магнитном поле
на такой атом действует сила
−∇V µ∇ .
В опытах Штерна и Герлаха (1921 г.) нейтральный атом пролетал
через поперечное неоднородное магнитное поле. В классической
электродинамике средняя действующая на атом сила F
z
µ
z
∂B
z
/∂z
может принимать любые значения из интервала −µ|∂B
z
/∂t|≤F
z
≤
µ|∂B
z
/∂z|, что приводило бы лишь к размытию на пластинке ли-
нии, вдоль которой осаждались пролетевшие атомы.
В квантовой механике
h и потому оператор
µ
L
−µ , µ
|e|h
m
e
c
— магнетон Бора.
Величина
µ
z
−µ L
z
принимает дискретный ряд значений
−µ
l, µ l − , ... , µ l,
что должно привести к появлению на пластинке
l полос. Опыт
частично подтвердил это предсказание, но для водорода и серебра
на пластинке оказалось две полосы, что формально соответствует
равенству
l ,тоестьl / .
73

Гипотеза Уленбека и Гаудсмита (1925 г.): электрон имеет соб-
ственный (не связанный с вращением вокруг ядра) момент импуль-
са и л и спин
h ,причемs
z
имеет собственные значения ± / .Сле-
дует отметить, что механическая модель электрона: шарик радиу-
са r
e
e / m
e
c вращается вокруг своей оси, несостоятельна, так
как моменту импульса
h/ ∼ m
e
r
e
v соответствует скорость враще-
ния v ∼
h/ m
e
r
e
∼ hc /e ∼ c !
Коммутационные соотношения (14.2) для компонент орбиталь-
ного момента определяются лишь общими свойствами операции по-
ворота, поэтому полученные в § 14 общие формулы справедливы и
для спина.
В частности,
s
m
,s
n
ε
mnk
s
k
,
откуда следует, что
s
z
,sи поэтому существуют совместные
собственные функции
s и s
z
s |s, mi s s |s, mi |s, mi s
z
|s, mi m |s, mi m ±s ± .
Введем краткие обозначения |s
,m i | i, |s ,m
− i |−i. Любое спиновое состояние |iможно представить в виде
|i
a|i a|−i, .
причем |a | |a | .
Из
s
z
| i | i следует
h
|s
z
| i , h−|s
z
| i
аналогично,
h
|s
z
|−i , h−|s
z
|−i − .
Набор матричных элементов hs, m
0
|s
z
|s, mi удобно представить в
виде матрицы
h |s
z
| i, h |s
z
|−i
h−|
s
z
| i, h−|s
z
|−i
−
.
Для операторов
l
±
l
x
± l
y
мы выводили соотношение
l
±
|l, mi
q
l ∓m l ± m |l, m ± i.
74

Подобным же образом получим s | i ,s |−i | i,тоесть
s
, s
−
s
,
s
x
ss
−
,s
y
s−s
−
−
.
Действие любого оператора
s
m
на произвольное состояние (24.1)
может быть описано, как действие соответствующей этому операто-
ру матрицы на спинор
χ
a
a
.
§25. Матрицы Паули. Уравнение Паули
Определим матрицы Паули σ
x
,σ
y
,σ
z
соотношением σ,тогда
σ
x
,σ
y
−
,σ
z
−
.
Их свойства:
σ
m
σ
n
Iδ
mn
ε
mnk
σ
k
, σ
m
, I .
Любую квадратную
× матрицу A можно представить в виде
A
a I σ,a A, Aσ .
Магнитный момент заряженной частицы, обусловленный ее ор-
битальным движением,
µ
l
связан с ее орбитальным моментом со -
отношением
µ
l
eh
mc
.
Связь же собственного момента частицы
µ
s
с ее спином ,какпо-
казывает опыт, зависит от вида частицы
µ
e
− , µ ≈−µ ,µ
|e|h
m
e
c
,
µ
p
, µ , µ
n
− , µ ,µ
|e|h
m
p
c
.
75
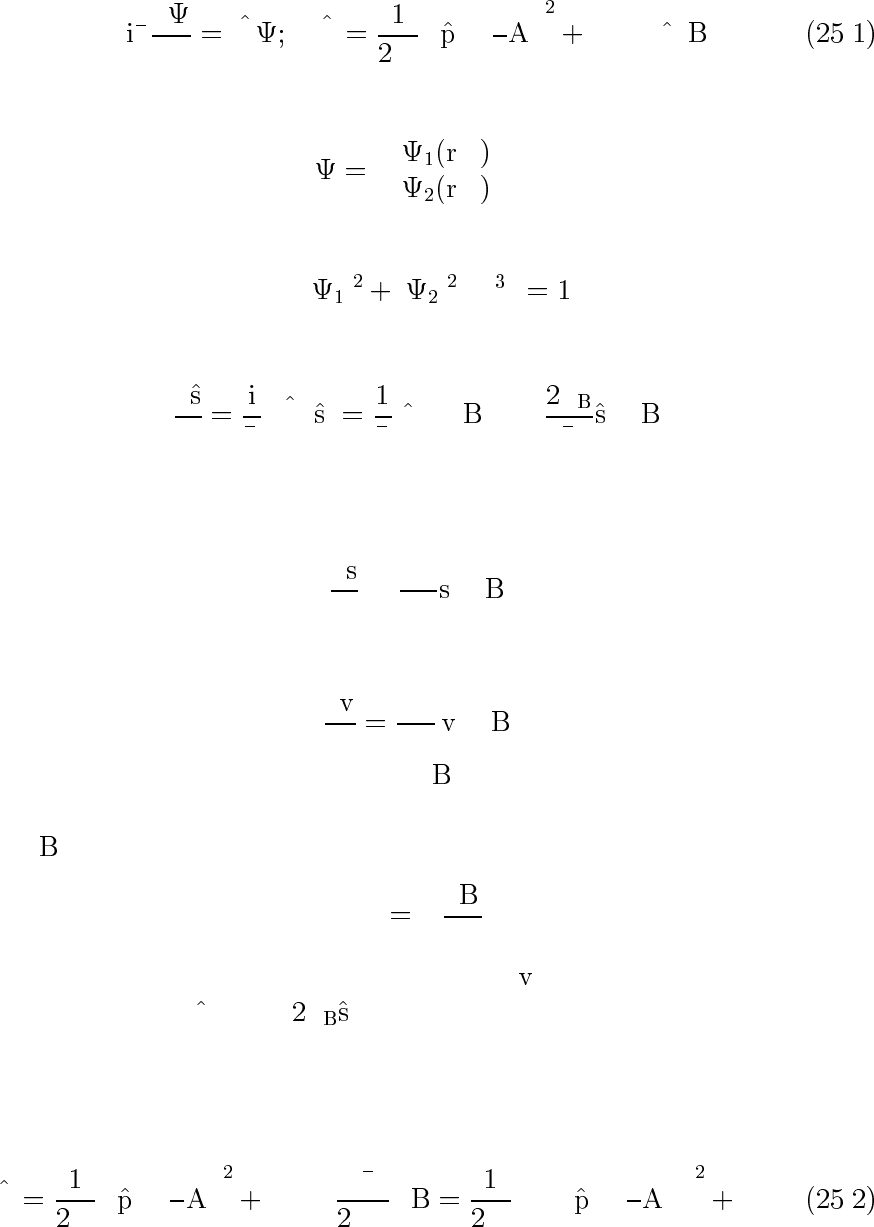
С учетом магнитного момента уравнение для движения частицы
в электромагнитном поле принимает вид (Паули, 1927 г.)
h
∂
∂t
H H
m
−
e
c
!
eϕ − µ
s
, .
в котором волновая функция — двухкомпонентный спинор
,t
,t
,
а условие нормировки таково:
Z
| | | |
d r .
Уравнение движения спина электрона в магнитном поле
d
dt h
h
H,
i
h
µ
e
× ≈−
µ
h
× .
В случае квазиклассичности движения электрона, усредняя это
уравение по квазиклассическому волновому пакету, получим для сред-
них значений
d
dt
≈
e
mc
× .
Аналогичное уравнение для скорости электрона имеет хорошо из-
вестный вид
d
dt
e
mc
× .
Таким образом, в магнитном поле
как вектор скорости, так и век-
тор спина электрона процессируют вокруг направления магнитного
поля
с одной и той же (циклотронной) частотой
ω
c
−
e
mc
.
Поэтому проекция спина на направление
остается неизменной (учет
малого отличия
µ
e
от − µ приводит к небольшому рассогласова-
нию этих скоростей).
Покажите, что имеет место соотношение
H
m
−
e
c
!
eϕ −
e
h
mc
σ
m
σ
−
e
c
!!
eϕ . .
(Оно окажется полезным в дальнейшем.)
76

§26. Сложение моментов
Рассмотрим две подсистемы с заданными моментами j и j .Сум-
марный момент
, величина его j может принимать различ-
ные значения. Примеры: система протон и нейтрон в s-состоянии
(при этом j
s / , j s / , —полный
спин системы); орбитальный и спиновый момент электрона в ато-
ме (j
l, j s / , l ) и т.д. Состояние подобной системы
можно описать двумя различными способами:
1) Набором собственных функций коммутирующих операторов
j
z
j
z
с собственными значениями j j m j j m :
m m
|j m i·|j m i
имеется всего N j j таких функций.
2) Набором собственных функций коммутирующих операторов
j
z
с собственными значениями j j m j j j j :
jm
|jmj j i.
При каждом j имеется
j различных значений m −j, −j
, ... , j, поэтому число таких функций (равное, конечно, N)есть
N
P
j
j , где сумма берется по всем допустимым при данных
j
и j значениях j.
Функции
m m
и
jm
должны быть снабжены также индексами j
и j , но так как эти значения фиксированы, мы их для упрощения
формул не выписываем явно.
Под проблемой сложения моментов понимаются следующие за-
дачи:
а) какие значения m возможны при заданных m
и m ?
б) какие значения j возможны при данных j
и j ?
в) ясно, что любая функция
jm
может быть выражена через ли-
нейные комбинации функций
m m
, и наоборот:
jm
X
m
m
C
jm
m
m
m m m m
X
jm
C
jm
m
m
jm
.
Как найти коэффициенты C и
C (их называют коэффициентами Клебша–
Гордана)?
Сформулируем ответы на эти вопросы:
77

а) Так как j
z
j
z
j
z
,то
m
m m.
б) Величина j принимает
j (при j >j )или j (при j <j )
значений
j
|j −j |, |j −j | , ... ,j j ,
причем интервал значений j между наименьшим j
|j − j | и
наибольшим j
j j значениями таков, как если бы отрезки
длиной j
,jиjсоставляли треугольник.
в) Поскольку
C
jm
m
m
h
jm
|
m m
i, C
jm
m
m
h
m m
|
jm
i,
то
C
jm
m
m
C
jm
m
m
∗
.
Если выбрать коэффициенты C
jm
m
m
вещественными, то
C
jm
m
m
C
jm
m
m
.
Конструктивный способ нахождения коэффициентов Клебша–Гордана
и доказательство ответа на вопрос б) мы укажем на двух простых
примерах.
Примеры
1. j
s / ,j s /, ≡ .
Имеется четыре функции:
| ↑↑i,
−
| ↑↓i,
−
| ↓↑i,
− −
| ↓↓i.
Та к как
S m m m , то в нашей системе
должен существовать триплет S
, m , ,− ,причем
| ↑↑i.
Две остальные функции
и
−
могут быть получены действием
понижающего оператора
S
−
s
−
s
−
на функцию ,чтодает
√
− −
| ↑↓i | ↓↑i
√
,
−
− −
| ↓↓i.
78
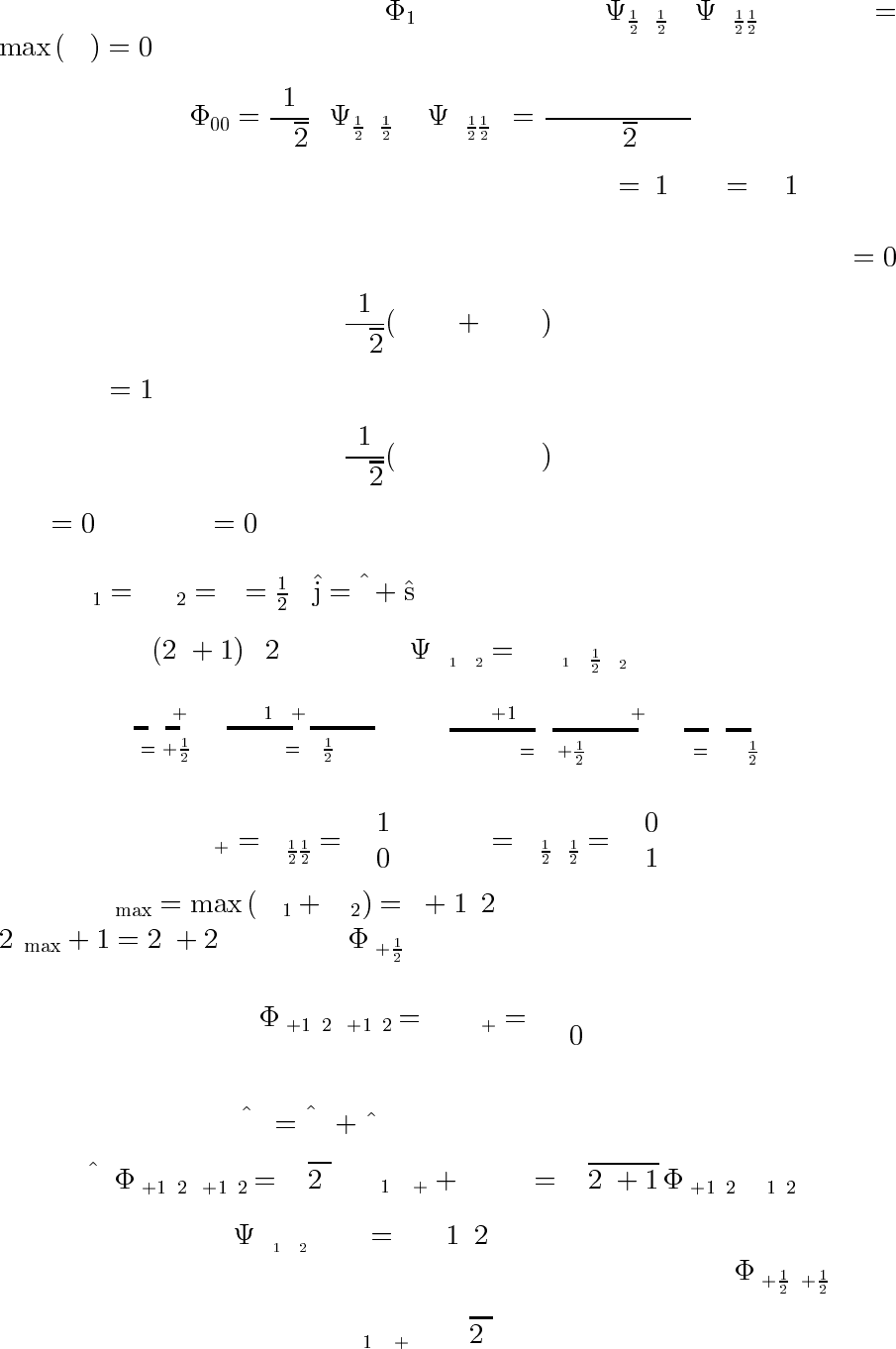
Оставшаяся ортогональная к
m
комбинация
−
−
−
имеет S
m . Это синглет
√
−
−
−
| ↑↓i− | ↓↑i
√
.
Еще проще: | ↑↑i и | ↓↓i соответствуют S
, m ± исим-
метричны по спинам. Симметрия функции не зависит от проекции
момента. Поэтому симметричная (нормированная) функция с m
√
| ↑↓i | ↓↑i
имеет S , а ортогональная к ней антисимметричная функция
√
| ↑↓i− | ↓↑i
с m имеет S .
2. j
l, j s , l .
Имеется
l ·функций
m m
Y
lm
χ
m
:
Y
ll
χ
| {z }
m
l
,Y
ll−
χ ,Y
ll
χ
−
|
{z }
m
l−
, ...,Y
l,−l
χ
−
,Y
l,−l
χ
| {z }
m
−l
,Y
l,−l
χ
−
|
{z }
m
−l−
,
где
χ
χ
,χ
−
χ
−
.
Та к как j
m m l/, то существует мультиплет из
j lфункций
l ,m
,причем
l / ,l /
Y
ll
χ
Y
ll
.
Остальные функции этого мультиплета могут быть получены дей-
ствием оператора
j
−
l
−
s
−
. В частности,
j
−
l / ,l /
√
lY
ll−
χ Y
ll
χ
−
√
l
l/ ,l− /
.
Из двух функций
m m
с m l − / , помимо указанной выше ком-
бинации, можно построить еще одну, ортогональную к
l ,l
:
Y
ll−
χ −
√
lY
ll
χ
−
.
79
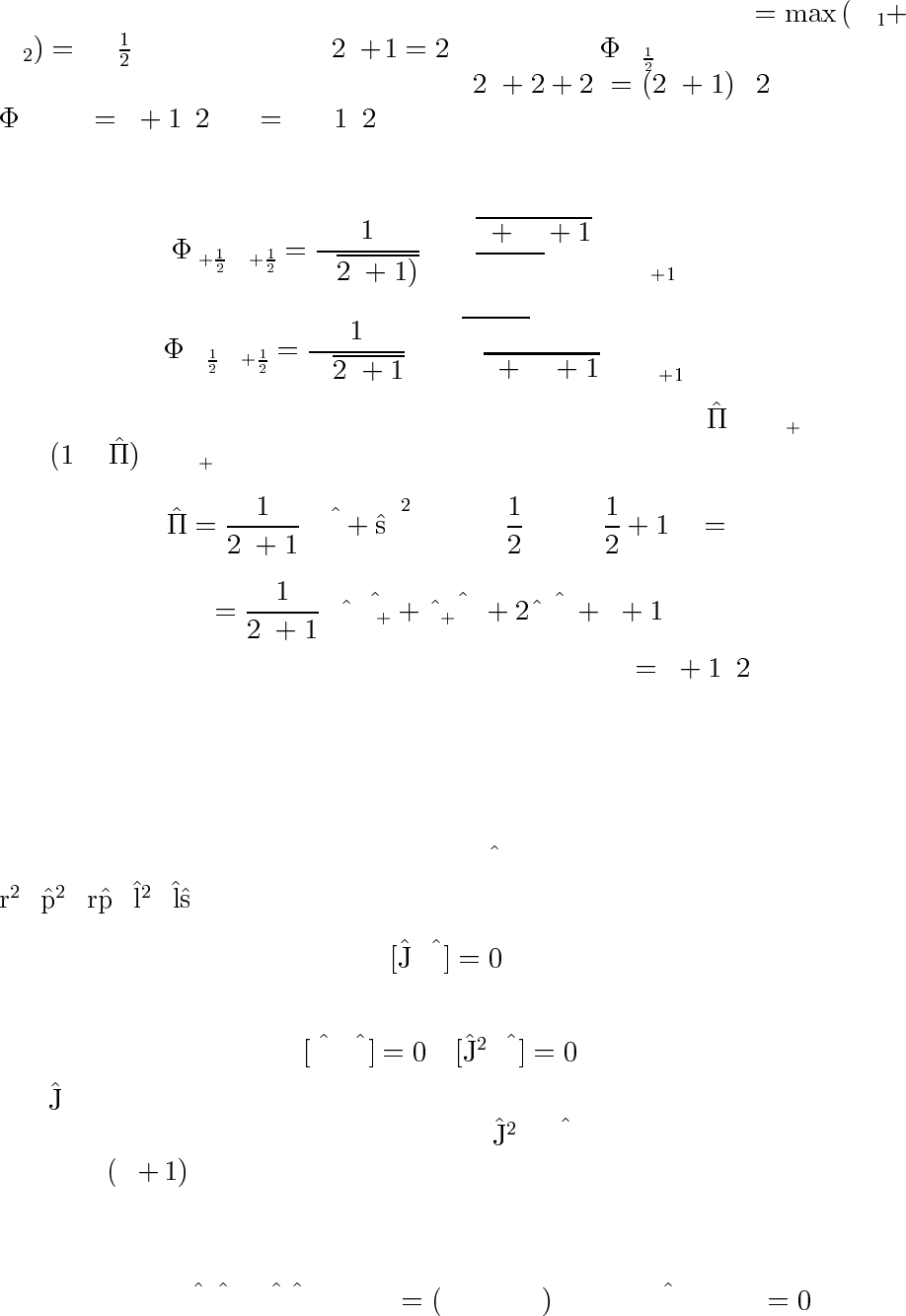
Ясно, что эта комбинация принадлежит к мультиплету с j m
m l−, содержащему j lфункцией
l− ,m
.Таким образом,
эти два мультиплета дают набор из
l ll ·функций
jm
с j l /иjl−/.
По ка жи те, ч то
l ,m
q
l
√
lmY
lm
√
l −mY
lm
,
l− ,m
√
l
√
l−mY
lm
−
√
l m Y
lm
.
Указание: первая из этих функций пропорциональна
Y
lm
χ ,авто-
рая
− Y
lm
χ ,где
l
"
l
−
l−
!
l−
!#
l
s
−
lsl
−
s
z
l
z
l
— проекционный оператор для мультиплета с j l /.
§27. Правила отбора для матричных элементов
скалярных и векторных операторов
Для каждого скалярного оператора S, построенного из операторов
, , ,,и т.д., справедливо
,S
или
J
z
,S , ,S ,
где
— оператор полного момента импульса системы. Пусть |JMαi
— собственная функция операторов
и J
z
с собственными значе-
ниями J
J иMсоответственно, набор квантовых чисел α хар ак-
теризует другие возможные физические величины, имеющие опре-
деленные значения в этом состоянии. Из соотношения
hJ
0
M
0
α
0
|J
z
S −SJ
z
|JMαi M
0
−M hJ
0
M
0
α
0
|S|JMαi
80
