Сербо В.Г., Хриплович И.Б. Конспект лекций по квантовой механике
Подождите немного. Документ загружается.

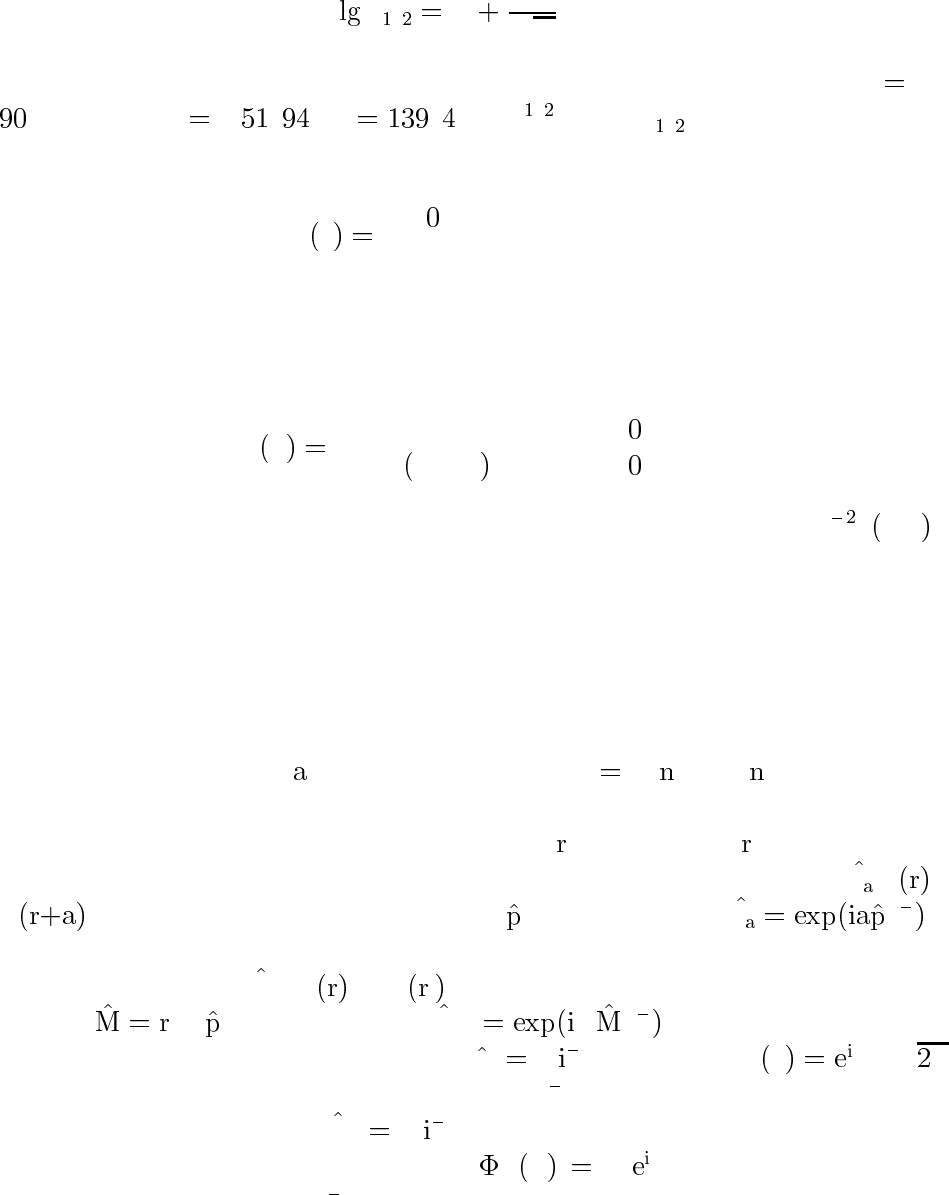
ная физика (М.: Наука, 1972 . С. 208). Эта зависимость (эмпириче-
ский закон Гейгера–Неттола) имеет вид
T
/
A
B
√
E
,
где A и B — константы, слабо зависящие от заряда ядра Z (для Z
известно A − , ; B , МэВ
/
,еслиT
/
в секундах).
Показать, что для α-частиц, движущихся в модельном потенциа-
ле
U
r
при r<a
α/r при r>a
и при условии E α/a, должен выполняться закон Гейгера–Неттола,
и найти вид коэффициентов A и B через параметры задачи.
13.2. Найти положение и ширину квазиуровней в поле
U
x
∞при x<
Gδ x−a при x> .
Специально обсудить случай малопроницаемого барьера G
h / ma
(ср. с задачей 4.56 ГКК).
§14. Момент импульса
Сдвиг и поворот
Сдвиг на расстояние
и поворот на угол α α ,где — произ-
вольный фиксированный единичный вектор, имеют ряд общих черт.
Пусть при таком повороте радиус-вектор
переходит в
0
.
В §11 было показано, что оператор сдвига, определенный как
T ψ ≡
ψ
, связан с оператором импульса соотношением T /h .
Совершенно аналогично можно показать, что оператор поворота,
определенный как
R
α
ψ ≡ ψ
0
, связан с оператором момента им-
пульса
× соотношением R
α
α /h .
Собственная функция оператора
p
z
− h∂/∂z равна ψ
k
z
kz
/
√
π
и соответствует собственному значению
hk. Аналогично, собствен-
ная функция оператора
M
z
− h∂/∂ϕ,гдеϕ— азимутальный угол
в сферических координатах, равна
m
ϕ A
mϕ
и соответствует
собственному значению
hm. На этом, однако, аналогия между сдви-
гом и поворотом кончается.
41
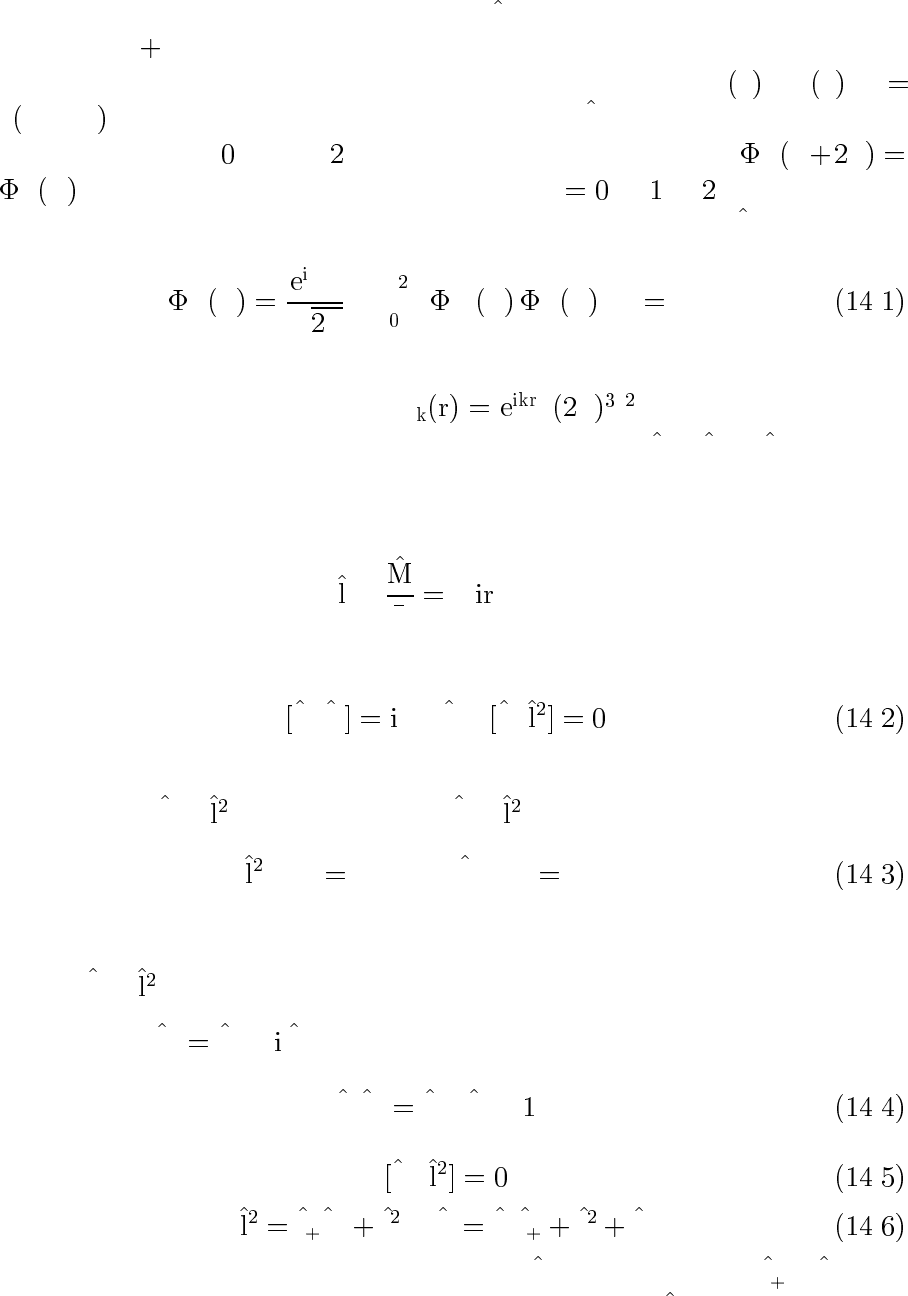
Собственная функция оператора p
z
определена на всей прямой,
−∞ <z<
∞, спектр оператора импульса непрерывный, а его соб-
ственные функции нормированы на δ-функцию:
R
∞
−∞
ψ
k
z
∗
ψ
k
0
z dz
δ k − k
0
. Собственная функция оператора M
z
определена в ограни-
ченной области,
≤ ϕ ≤ π, требование однозначности
m
ϕ π
m
ϕприводит к дискретному спектру m , ± , ± ,.... Ортонор-
мированная система собственных функций оператора
M
z
такова:
m
ϕ
mϕ
√
π
,
Z
π
∗
m
0
ϕ
m
ϕdϕ δ
mm
0
. .
Далее, различные компоненты оператора импульса коммутируют
друг с другом, плоская волна ψ
/ π
/
представляет собой
совместную собственную функцию операторов
p
x
, p
y
и p
z
. Напро-
тив, различные компоненты оператора момента импульса не комму-
тируют друг с другом. Введем безразмерный оператор
≡
h
− ×∇.
Нетрудно показать, что
l
j
,l
k
ε
jks
l
s
, l
j
, . .
Отсюда видно, что можно искать совместные собственные функции
операторов
l
x
и или операторов l
z
и :
ψ
λm
λψ
λm
, l
z
ψ
λm
mψ
λm
. .
Свойства собственных функций и собственных значений опера-
тор ов
l
z
и , следующие из коммутационных соотношений
Определим
l
±
l
x
± l
y
,тогда
l
z
l
±
l
±
l
z
±
, .
l
±
, , .
l l
−
l
z
− l
z
l
−
l l
z
l
z
. .
Соотношение (14.4) между оператором l
z
и операторами l и l
−
ана-
логично соотношениям (7.1) между оператором
H и повышающим
42
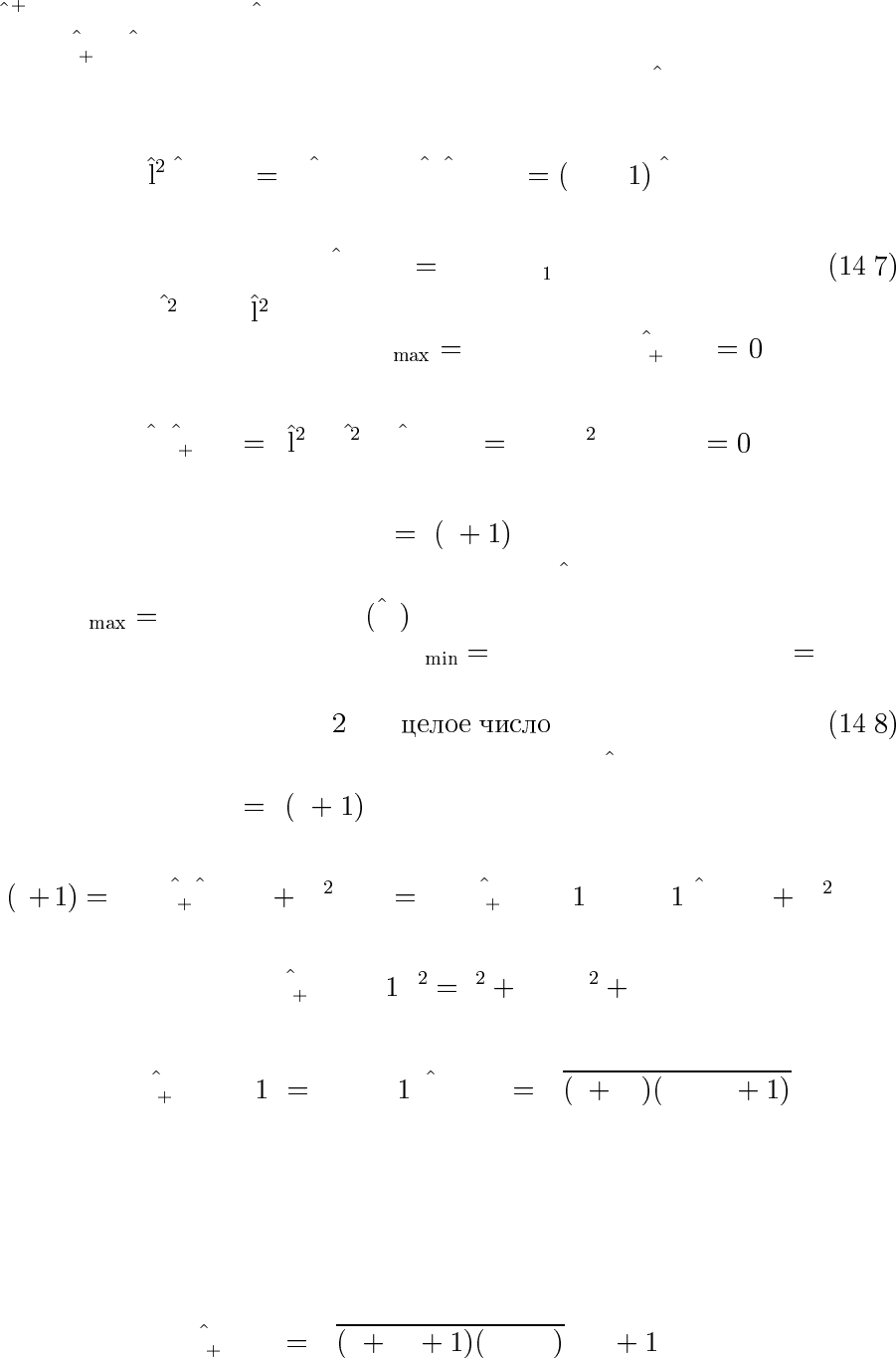
a и понижающим a операторами для осциллятора. Поэтому опера-
торы
l и l
−
будут играть роль повышающих и понижающих опера-
торов для состояний с определенным значением
l
z
. Действительно,
из (14.4–5) следует
l
±
ψ
λm
λ l
±
ψ
λm
, l
z
l
±
ψ
λm
m ± l
±
ψ
λm
,
то ес т ь
l
±
ψ
λm λm
ψ
λm±
. .
Поскольку hl
z
i≤hi, то при заданном λ существует максимальное
значение m, о бознач им е го m
l.Ясно,чтоl ψ
λl
, отсюда с
учетом (14.6) получаем
l
−
l ψ
λl
− l
z
− l
z
ψ
λl
λ − l − l
ψ
λl
или
λ
l l .
Применяя n раз понижающий оператор
l
−
к состоянию с наиболь-
шим m
l,мыполучим l
−
n
ψ
λl
∝ ψ
λl−n
. Увели чива я n,мыпри-
дем к наименьшему значению m
−l, в этом слу ча е l −n −l,то
ест ь
l − . .
Найдем матричные элементы операторов l
±
. Будем обозначать
состояние ψ
λm
с λ l l ка к |lmi и усредним (14.6) по этому со-
стоянию, тогда
l
l hlm|l l
−
|lmi m −m hlm|l |lm− ihlm− |l
−
|lmi m −m,
то ес т ь
|hlm|
l |lm − i| l l − m m.
Отсюда следует , что
hlm|
l |lm − i hlm − |l
−
|lmi
q
l m l − m .
Извлекая квадратный корень, мы выбрали определенный (поло-
жительный) знак, что соответствует фиксированию фазовых соот-
ношений между различными состояниями |lmi с данным l.
Полученные формулы определяют также и коэффициенты C всо-
отношении (14.7)
l |lmi
q
l m l − m |lm i,
43

l
−
|lmi
q
l m l − m |lm − i. .
В заключение этого раздела укажем, что нетрудно проверить сле-
дующие обобщение коммутационных соотношений (14.2):
l
j
,A
k
ε
jks
A
s
, l
j
, ,.
где ,или ,или или векторная функция вида
f ff,f
j
≡f
j
, , .
Сферические функции
Для получения конкретного вида собственных функций удобно ис-
пользовать сферические координаты, в которых
l
z
−
∂
∂ϕ
,
l
±
± ϕ
±
∂
∂θ
θ
∂
∂ϕ
!
,
−
θ
∂
∂θ
θ
∂
∂θ
θ
∂
∂ϕ
.
Совместные собственные функции операторов
и l
z
удобно искать
в виде Y
lm
θ, ϕ
lm
θ
m
ϕ, где функция
m
ϕ определена в
(14.1) с m
, ± , ± ,..., ±l. Для нахождения функции
lm
θ мож-
но использовать такой прием. Условие
l Y
ll
приводит к уравне-
нию
d
dθ
− l
θ
!
ll
θ ,
откуда получаем Y
ll
lϕ
l
θ. Последовательно применяя по-
нижающий оператор в соответствии с (14.9), получим сферические
функции
Y
lm
θ, ϕ −
m |m|
v
u
u
u
t
l
π
l−|m|
l |m|
P
m
l
θ
mϕ
,
где P
m
l
x — присоединенные полиномы Лежандра. Сферические
функции образуют ортонормированую систему
Z
Y
∗
l
0
m
0
Y
lm
d δ
ll
0
δ
mm
0
.
Отражение системы координат
→− в сферических координа-
тах выглядит так: r → r, θ → π −θ, ϕ → ϕ
π. Пр и этом
Y
lm
− −
l
Y
lm
.
44
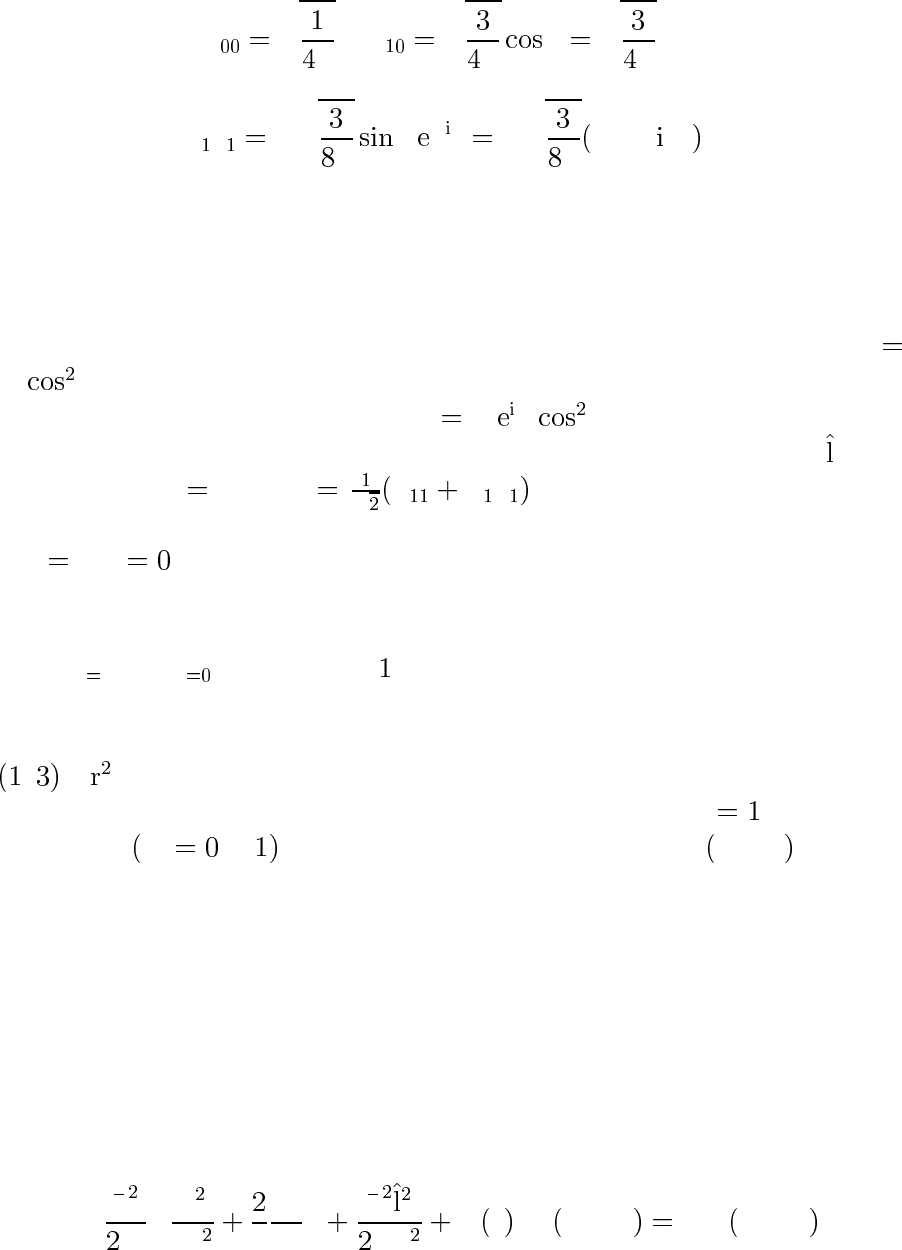
Примеры
Y
v
u
u
t
π
,Y
v
u
u
t
π
θ
v
u
u
t
π
n
z
,
Y
±
±
v
u
u
t
π
θ
± ϕ
±
v
u
u
t
π
n
x
± n
y
.
ВОПРОСЫ
14.1. В состоянии частицы, заданном волновой функцией ψ
A ϕ, найти вероятности различных значений m проекции мо-
мента на ось z и hl
z
i.Тожедляψ A
ϕ
ϕ.
14.2. Обсудить вопрос о том, куда направлен вектор hψ|
|ψi в
состояниях ψ
Y
ll
и ψ
√
Y Y
−
. Показать, что в состоянии
ψ
m
с определенной проекцией момента m на ось z средние значения
hl
x
i hl
y
i .
14.3. Исследовать качественно угловое распределение плотности
вероятности для состояний, описываемых сферическими функция-
ми Y
l,m l
и Y
l,m
,считаяl .
14.4. Указать, при каких m и m
0
могут быть отличны от нуля ма-
тричные элементы дипольногоhm
0
|x
i
|miи квадрупольного hm
0
|x
i
x
j
−
/ δ
ij
|mi моментов.
14.5. Частица находится в состоянии с моментом l
и его про-
екцией m
m , ± на ось z. Найти вероятности W m
0
,m различ-
ных значений проекции момента m
0
на ось z
0
, составляющ ую угол α
сосьюz. Рассмотреть, в частности, случай, когда ось z
0
перпенди-
кулярна оси z (задача 3.24 ГКК).
§15. Центральное поле
Для центрального поля удобны сферические координаты. УШ в них
имеет вид
−
h
m
∂
∂r r
∂
∂r
h
mr
U r
ψ r, θ, ϕ Eψ r, θ, ϕ .
45

Его можно легко получить, используя тождество
h
r
− ×
r
× − ·
r
·
Разделяя переменные ψ R r Y
lm
θ, ϕ , получим для радиальной
функции уравнение
−
h
m
∂
∂r r
∂
∂r
U r
R
l
E
l
R
l
,U U r
hll
mr
.
От первой производной по r можно избавиться заменой R
l
χ
l
/r.
Для χ
l
r получаем обычное одномерное уравнение Шредингера
−
h
m
χ
00
l
U r χ
l
E
l
χ
l
,
но с эффективным потенциалом U
r , зависящим от l. Из того, что
R
l
r конечно в нуле, следует χ
l
. Условие нормировки таково:
Z
∞
|χ
l
r | dr .
Терминология. l
, , , , ... s,p,d,f,... — азимутальное, m —
магнитное квантовые числа. Радиальное квантовое число n
r
равня-
ется числу узлов функции χ
l
r (кроме точек r и r ∞).
Поведение при r →
. Пусть r U r → при r → , тогда решени-
ями уравнения
χ
00
l
l l
r
χ
l
служат
χ
l
ar
l
R
l
ar
l
и χ
l
b
r
l
R
l
b
r
l
.
Второе решение сингулярно и поэтому не годится. Отметим, что
ψ
6 лишь для l .
Поведение при r →∞. Считая, что поле убывает достаточно бы-
стро, получим
χ
00
l
−
mE
h
χ
l
,
так что
χ
l
∝
± kr
kr α
l
E> ,
−κr
E< .
46
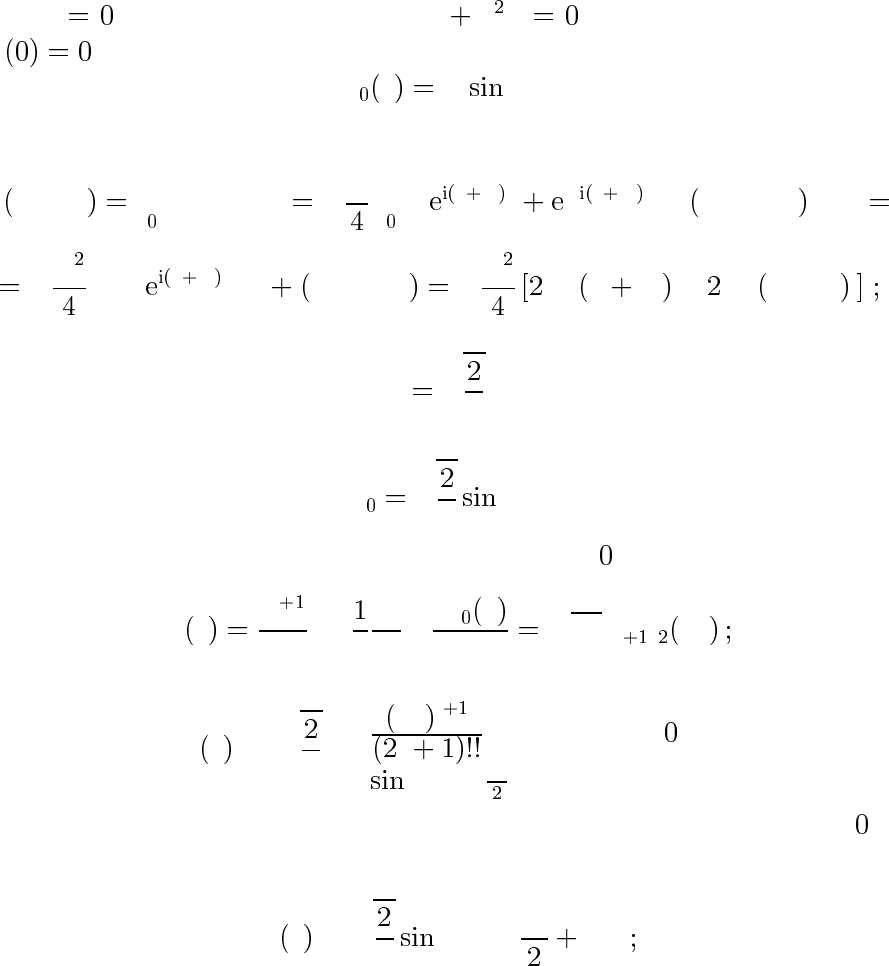
Свободное движение
При l
решением уравнения χ
00
k χ с граничным условием
χ
служит
χ
k
r Akr .
Нормировка на δ-функцию “по шкале k”:
δ
k −k
0
Z
∞
χ
k
0
χ
k
dr −
A
Z
∞
h
k k
0
r −k k
0
r
− k →−k
i
dr
−
A
Z
∞
−∞
k k
0
r
dr k→−k −
A
πδ k k
0
− πδ k−k
0
отсюда следует
A
v
u
u
t
π
.
Витоге
χ
k
v
u
u
t
π
kr .
Можно показать (см. КМ § 33), что при l>
χ
kl
r
r
l
k
l
−
r
d
dr
!
l
χ
k
r
r
√
krJ
l /
kr
отсюда
χ
kl
r →
v
u
u
t
π
·
kr
l
l
при r → ,
kr −
πl
при r →∞.
Если поле убывает при r →∞достаточно быстро, то при E>
и
боль ши х r движение становится свободным, поэтому
χ
kl
r ≈
v
u
u
t
π
kr −
πl
δ
l
!
зд есь δ
l
— так называемая фаза рассеяния.
ВОПРОСЫ
15.1. Показать, что задача 1 из § 33 КМ сводится к вопросу 5.1.
15.2. Задача 3 из того же § 33.
15.3. Задача 4.20 ГКК. Как меняются значения E
n
r
l
энергетиче-
ских уровней частицы в дискретном спектре:
47
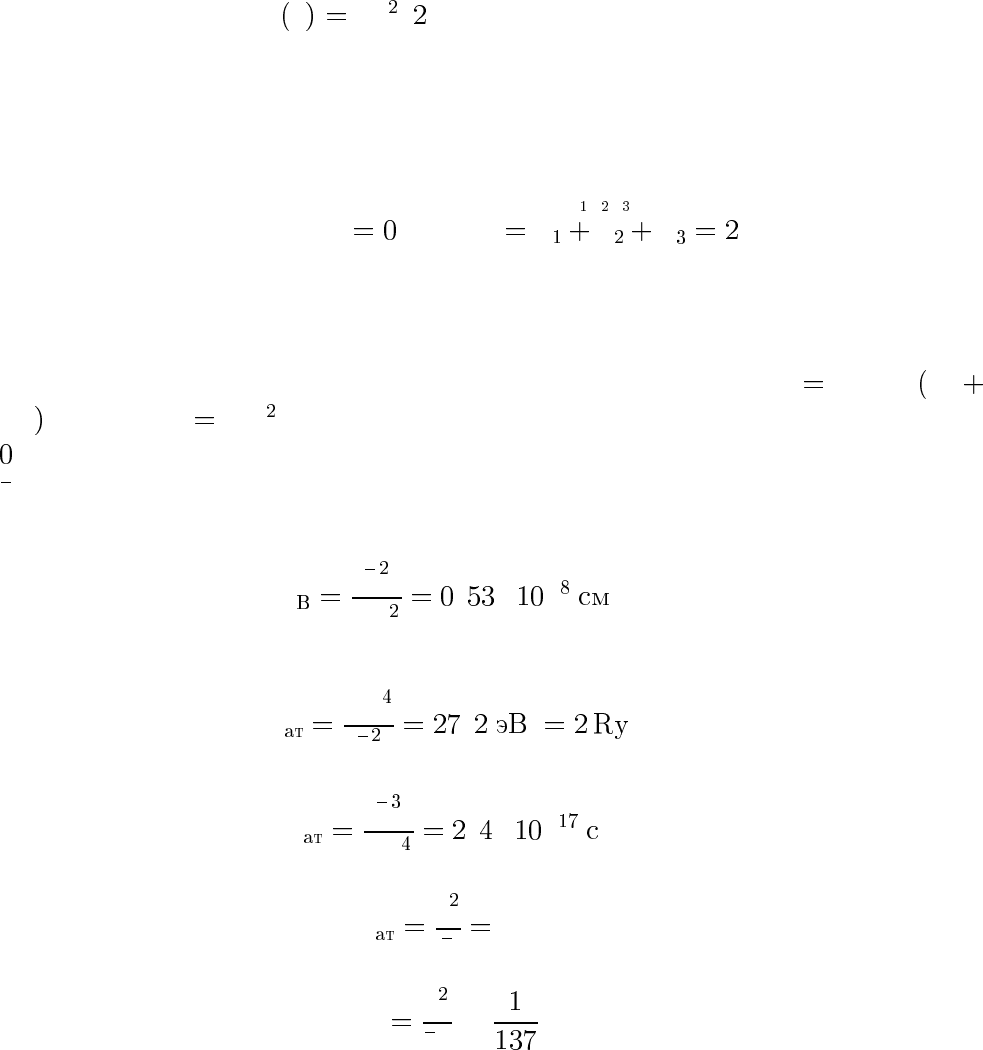
а) при фиксированном значении l с увеличением n
r
;
б) при фиксированном значении n
r
с увеличением l?
15.4. Задача 4.21 ГКК. Для частицы, находящейся в центральном
поле,
а) могут ли быть двукратно вырожденные уровни;
б) какую кратность вырождения может иметь первый возбужденный
уровень?
15.5. Задачи 4.23 ГКК и 4.24 ГКК. Найти уровни энергии и нор-
мированные волновые функции стационарных состояний сфериче-
ского осциллятора U
r kr / , используя декартовы координаты.
Определить кратность вырождения уровней.
Произвести классификацию четырех нижних уровней осциллято-
ра по n
r
,lи четности, исходя только из известного значения крат-
ности вырождения уровней.
Какая комбинация волновых функций ψ
n n n
отвечает состоянию
осциллятора с моментом l
(при N n n n )?
§16. Атом водорода
Задача сводится к движению частицы приведенной массы m m
e
m
p
/ m
e
m
p
вполеU −e/r, ниже рассматривается только случай E<
(связанные состояния). Естественная система единиц включает
h, e, m. Из них строятся единицы
длины (боровской радиус)
a
h
me
, ·
−
,
энергии (удвоенный Ридберг)
E
me
h
, ,
времени
t
h
me
, ·
−
,
скорости
v
e
h
αc ,
где
α
e
hc
≈
48

— так называемая постоянная тонкой структуры. (Найдите единицы
импульса, силы, напряженности электрического и магнитного по-
лей.) Переходя к безразмерным величинам r
0
r/a , E
0
E/E ,
получим УШ в виде
d
χ
l
dr
0
E
0
r
0
−
l
l
r
0
χ
l
.
В дальнейшем штрихи опускаем.
Мы знаем, что χ
l
∼ r
l
при r → и χ
l
∼
−κr
при r →∞(здесь
κ
√
− E). Поэтому ищем решение в виде
χ
l
r
l −κr
w r .
Для w
r получаем уравнение
rw
00
l−κr w
0
− κ − κl w .
Его решение ищем в виде ряда w
P
∞
s
a
s
r
s
. Рекуррентное соотно-
шение для коэффициентов таково:
a
s
κ s l −
ss l
a
s
.
Из него получаем
a
s
→
κ
s
a
s
s →∞.
Та ки м о бр азом, a
s
≈ κ /s и, если ряд не оборвать, он сходится
к w ∼
κr
при r →∞.Чтобыχ
l
r → при r →∞, н еобходи мо
оборвать ряд на некотором s
n
r
. П ри этом κ n
r
l −и
w
rL
n
r
r— полином степени n
r
,имеющийn
r
узлов (он сводится
к полиному Лагерра). В итоге,
E
n
−
n
,ψ
nlm
R
lm
r Y
lm
θ, ϕ ,R
nl
r
l −r/n
L
n
r
r ,
n
n
r
l ,,,... , n
r
, , ,... , l , ,..., n− .
Кулоновское вырождение. Уровню E
n
с данным главным кван-
товым числом n соответствует
n−
X
l
l n
49
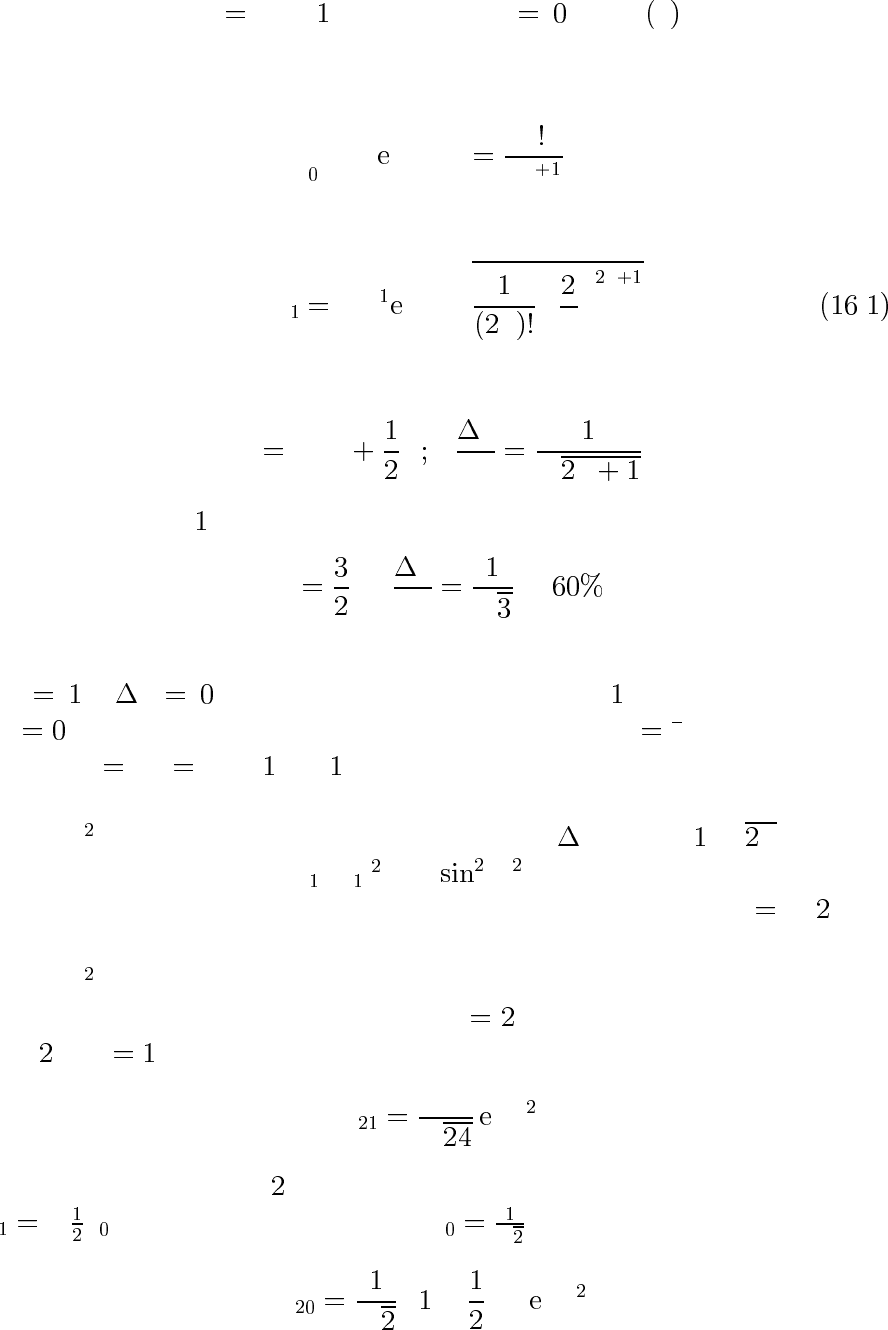
различных состояний (различных волновых функций).
Состояния с l
n − . Для них n
r
и L
n
r
r — просто кон-
станта, которую легко определить из условия нормировки, исполь-
зуя известный интеграл
Z
∞
x
n −αx
dx
n
α
n
.
Таким образом, получим
R
n,n−
r
n− −r/n
v
u
u
u
t
n
n
!
n
. .
Отсюда найдем, что в данном состоянии
hri
n
n
!
r
hri
√
n
.
У основного
s состояния
hri
,
r
hri
√
≈ .
Таким образом, здесь нет сходства с моделью Бора, для которой
hri
, r (не говоря уже о том, что в s состояние момент
M
, а в модели Бора в основном состоянии M h).
При l
m n − , напротив, квантовая механика дает от-
вет, близкий к боровской модели. А именно, средний радиус велик:
hri≈n
, относительная дисперсия мала: r/hri≈ /
√
n,вугло-
вом распределении |Y
n− ,n−
| ∝
n−
θ вероятность найти элек-
трон сконцентрирована в узком интервале углов вблизи θ
π/ ,что
очень похоже на классическую траекторию в форме окружности ра-
диуса n
вплоскостиxy.
Первый возбужденный уровень n
. Волновая функция состоя-
ния
p с l (см. (16.1))
R
r
√
−r/
не имеет узлов. Для s состояния рекуррентное соотношение дает
a
− a , а условие нормировки a
√
,итого
R
√
− r
!
−r/
,
50
