Сербо В.Г., Хриплович И.Б. Конспект лекций по квантовой механике
Подождите немного. Документ загружается.

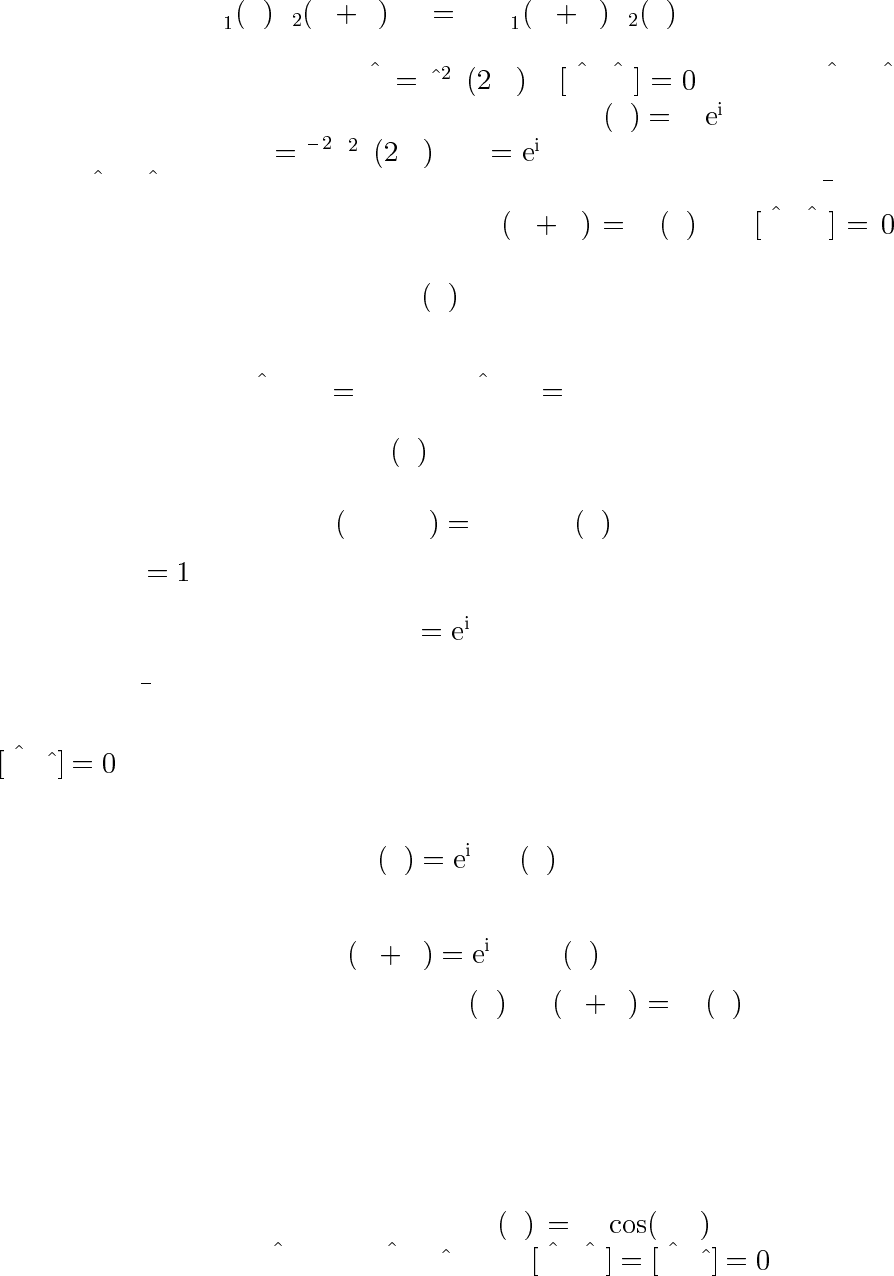
Оператор сдвига неэрмитов:
Z
ψ
∗
x ψ x a dx 6
Z
ψ
∗
x a ψ x dx .
Для свободной частицы
H p / m и H,T
a
,потомуHиT
a
имеют совместные собственные функции ψ
Eλ
x A
kx
ссобствен-
ными значениями E
h k / m и λ
ka
. Импульс тоже коммути-
ру ет с
H и T
a
и имеет в этом состоянии собственное значение hk.
Если потенциал периодический, U
x a U x ,то H,T
a
.
В таком поле собственные функции стационарных состояний могут
быть выбраны в таком виде, ψ
Eλ
x , что они одновременно являются
собственными функциями оператора сдвига:
Hψ
Eλ
Eψ
Eλ
, T
a
ψ
λ
λψ
Eλ
.
Если потребовать, чтобы ψ
Eλ
x была конечной при x →±∞,тоиз
соотношения
ψ
Eλ
x ±na λ
±n
ψ
Eλ
x
следует |λ| ,тоестьλможно представить в виде
λ
qa
.
Величину
hq в этом случае называют квазиимпульсом.Конечно,
истинный импульс не сохраняется в периодическом поле, так как
H,p 6 .
Если такое решение переписать в виде
ψ
Eλ
x
qx
u
q
x ,
то из
ψ
Eλ
x a
qa
ψ
Eλ
x
следует периодичность функции u
q
x : u
q
x a u
q
x . Это утвер-
ждение называется теоремой Блоха.
ВОПРОСЫ
11.1. Для свободного движения ψ
x A x/b является соб-
ственной функцией
H,нонеT
a
иp,хотя H,T
a
H,p .Почему?
31
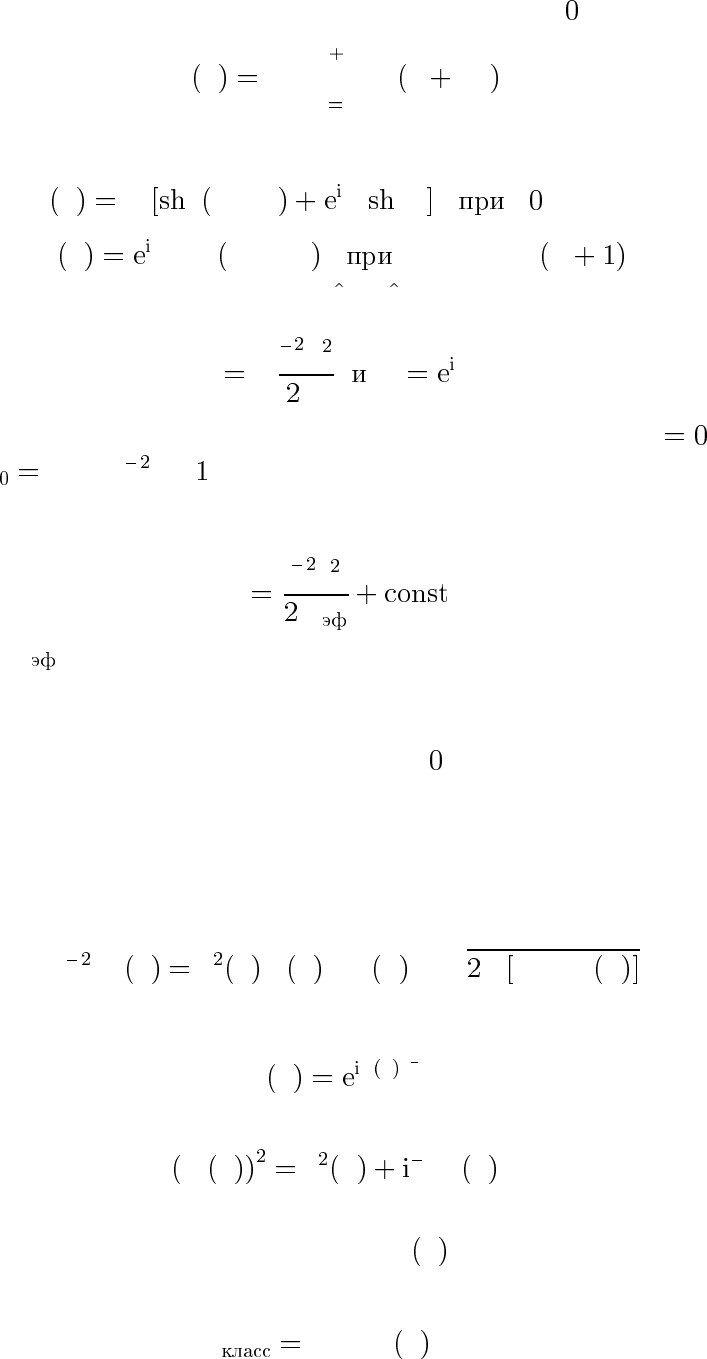
11.2. Рассматривается движение частицы с E< вполе
U
x −G
∞
X
n
−∞
δ x na .
Покажите, что волновая функция, определенная соотношениями
ψ
q
x Aκ a − x
qa
κx <x<a,
ψ
q
x
qna
ψ
q
x −na na < x < n a,
является собственной функцией
H и T
a
с собственными значениями
E
−
h κ
m
λ
qa
.
Найдите связь между E и λ из условия сшивки ψ
0
/ψ при x .
При κ
mGa/h разрешите это уравнение и найдите в явном
виде зависимость E от q. Представив при малых q эту зависимость
в виде
E
h q
m
,
найдите m
. Найдите плотность тока j
x
и покажите, что одному
значению E при разных значениях q соответствуют разные j
x
.
Как ведет себя классическая частица в данном поле?
Повторите это рассмотрение для E>
.
§12. Квазиклассическое приближение
Подставив в УШ
−
h ψ
00
x pxψx,px≡
q
mE−Ux
волновую функцию в виде
ψ
x
Sx/h
,
получим
S
0
x p x hS
00
x .
Если отбросить последнее слагаемое, то получим классическое урав-
нение Гамильтона–Якоби, в котором S
x — действие как функция
координат. Решение этого уравнения
S
±
Z
x
p x dx .
32
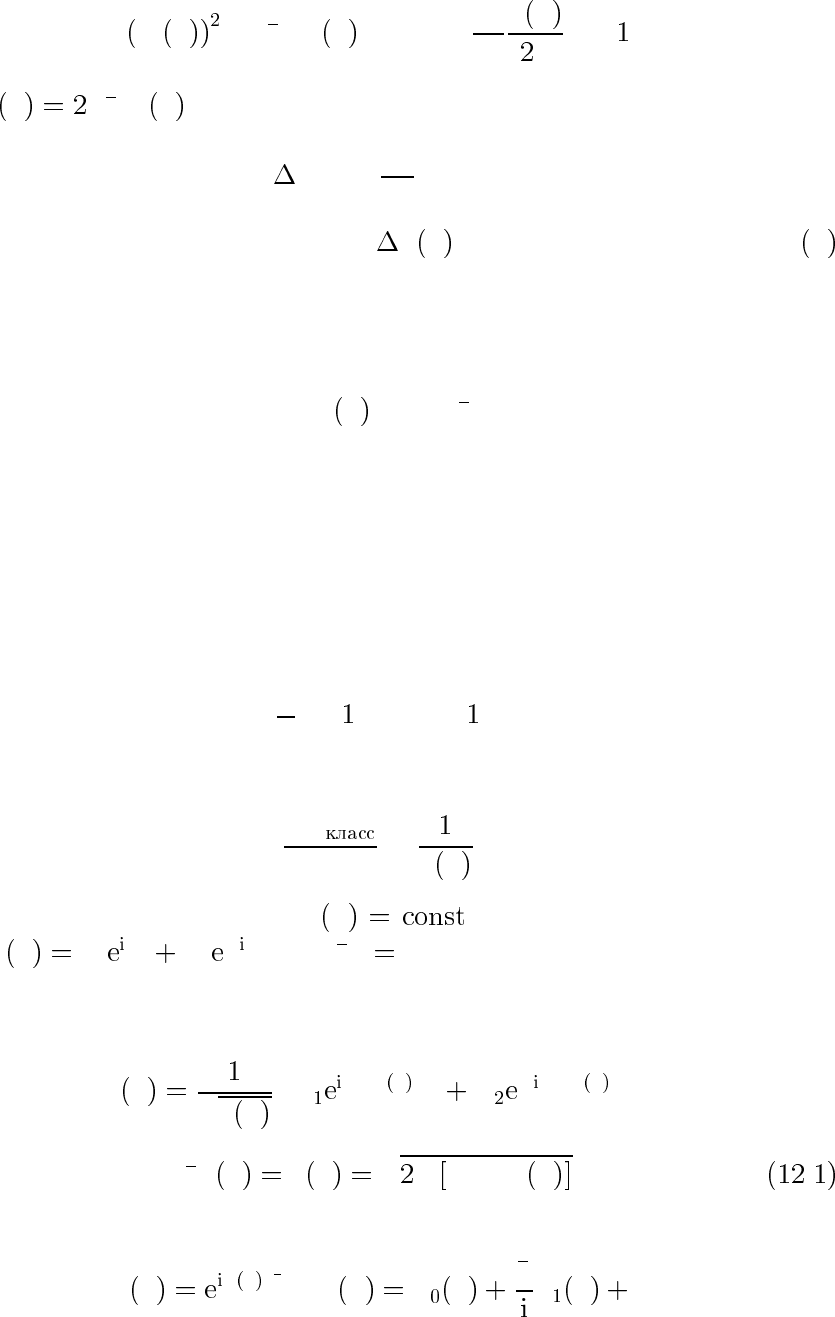
Таким образом, переход к классике происходит , когда
S
0
x h|S
00
x | или
d
dx
λ
x
π
,
где λ
x πh/p x .Иначе,
λ∼λ
dλ
dx
λ,
то есть изменение длины волны
λ x на расстоянии порядка λ x
должно быть много меньше длины волны.
Другая форма критерия — великость классического действия по
сравнению с квантом действия
Z
p x dx
h.
Подчеркнем, наконец, что переход к квазиклассическому пределу
в квантовой механике — это аналог перехода к пределу геометриче-
ской оптики в оптике волновой. И критерии применимости у этих
пределов общие: длина волны λ должна быть много меньше, чем ха-
рактерные расстояния a, на которых меняется потенциал (в оптике
— коэффициент преломления):
λ
a
,ka.
В классической механике плотность вероятности
dW
dx
∝
v x
.
В квантовой механике при U
x точное решение УШ имеет
вид ψ
x A
kx
B
− kx
,гдеhk p. Естественно ожидать, что для
движения частицы в достаточно плавно изменяющемся поле при-
ближенное решение выглядит так:
ψ
x
q
kx
C
R
x
kxdx
C
−
R
x
k x dx
,
hk x px
q
mE−Ux. .
Чтобы показать это, подставим
ψ
x
Sx/h
,Sx Sx
h
Sx...
33

в УШ и удержим члены первого порядка по h:
S
0
− hS
0
S
0
− hS
00
p x .
Отсюда
S
x Sx ±
Z
pxdx , S
0
−
S
00
S
0
−
d
dx
p x ,
то ес т ь
S
x
q
p x
,
что и приводит к (12.1). В классически недоступной области
ψ
x
q
κ x
C
R
x
κ x dx
C
−
R
x
κ x dx
,
hκ x
q
mUx−E..
Правила квантования Бора-Зоммерфельда
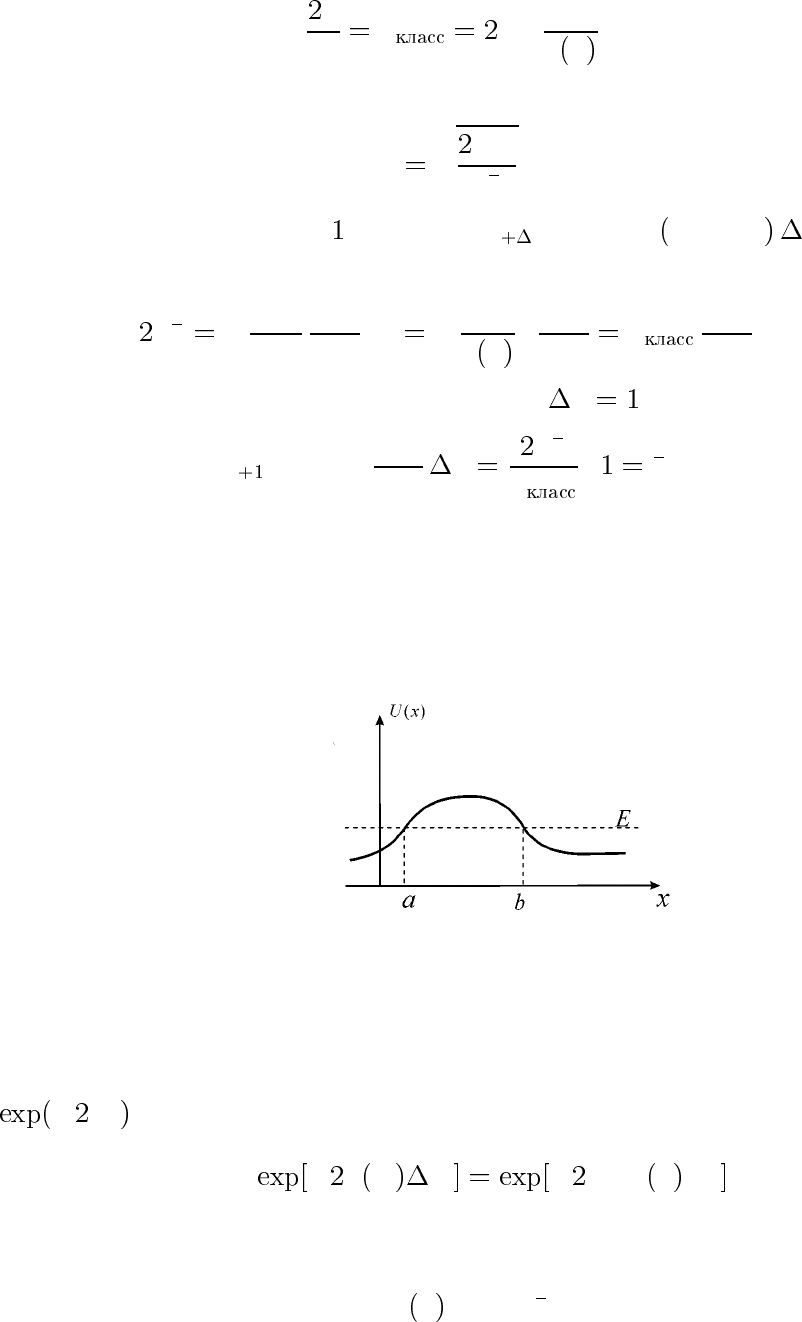
Рассмотрим движение частицы в квазиклассическом поле вида рис.
7. В квазиклассическом приближении волновая функция связанного
состояния при x<a(область A на рис. 7) — это волна, затухающая
при x →−∞:
ψ
A
x
A
√
κ
−
Z
a
x
κdx
при x>b(область C на рис. 7), аналогично,
ψ
C
x
C
√
κ
−
Z
x
b
κdx
.
В классически доступной области a<x<bволновую функцию
можно записать в виде стоячей волны
ψ
B
x
B
√
k
Z
x
a
kdx α
.
Правила сшивки при переходе точки поворота a (идею сшивки мож-
но найти, например, в книге Давыдова А.С. Квантовая механика
(М.: Наука, 1973; §23) таковы:
A
B, α
π
.
34
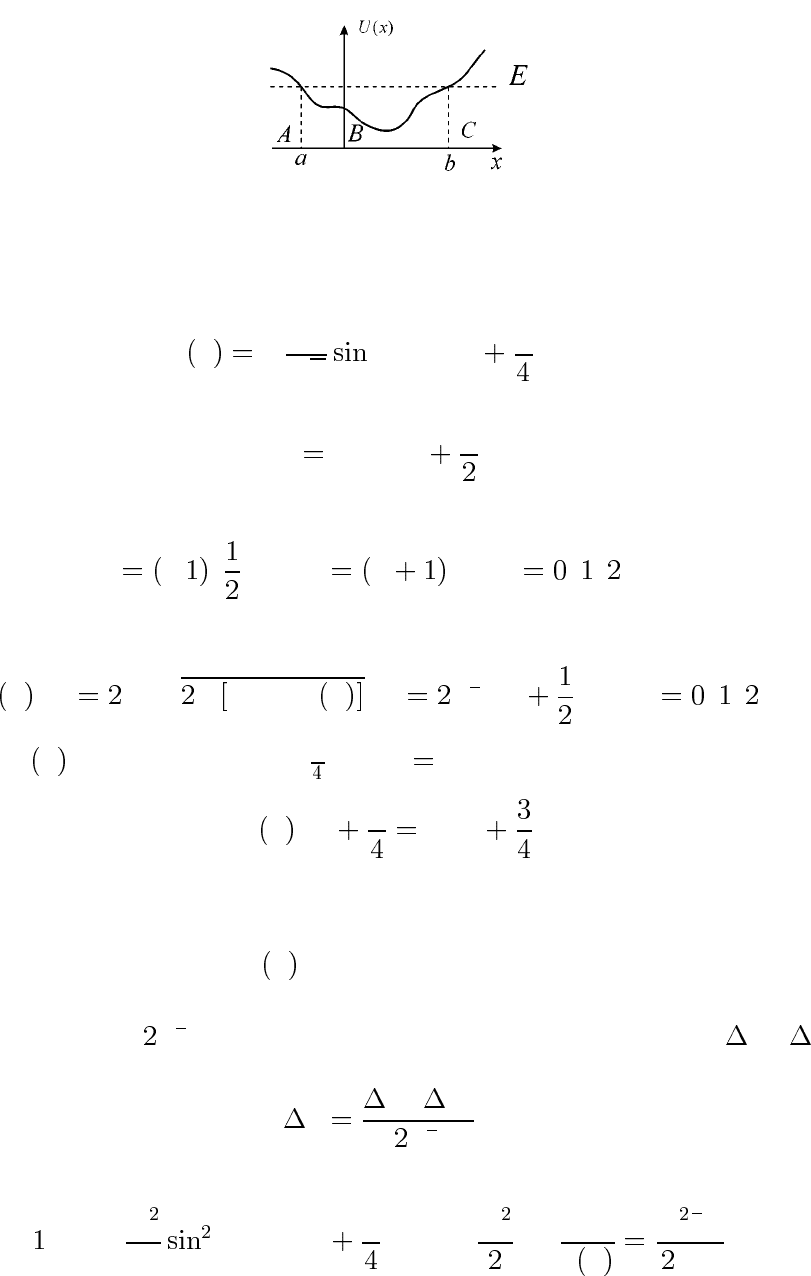
Рис. 7: Квазикла ссиче ская потенциаль ная яма
Переписав ψ
B
в виде
ψ
B
x −
B
√
k
Z
b
x
kdx
π
−β
!
,
где
β
Z
b
a
kdx
π
,
и применив сшивку в точке b, находим
C
−
n
B, β n π, n , , ,....
Таким образом, получаем правило квантования:
I
p x dx
Z
b
a
q
m E
n
− U x dx πh
n
!
,n ,,,....
Вψ
B
x фаза меняется от
π
при x a до
Z
b
a
k x dx
π
π
n
!
,
так что волновая функция, отвечающая уровню E
n
,имеет,всоот-
ветствии с осцилляционной теоремой, n узло в.
Фазовая площадь
H
p x dx растет линейно с ростом числа состо-
яний n, так что в фазовом пространстве на каждое состояние прихо-
дится площадь
πh,ачисло состояний в фазовой ячейке x · p
x
равно
n
x · p
x
πh
.
Нормировка волновой функции:
≈
Z
b
a
B
k
Z
x
a
kdx
π
!
dx ≈
B
Z
b
a
dx
k x
B hπ
mω
,
35
где
π
ω
T
Z
b
a
dx
v x
— классический период колебаний. Отсюда
B
v
u
u
t
mω
πh
.
В квазиклассике n
,такчтоE
n n
− E
n
≈ dE
n
/dn n. Про-
дифференцируем по n правило квантования
πh
I
∂p
∂E
n
dE
n
dn
dx
I
dx
v x
·
dE
n
dn
T
dE
n
dn
.
Отсюда разность соседних уровней (при
n )составляет
E
n
− E
n
≈
dE
n
dn
n
πh
T
· hω .
Иными словами, в каждом небольшом участке квазиклассиче-
ской части спектра уровни эквидистантны.
Рис. 8: Квазикласс иче ский барьер
Подбарьерное прохождение
Для прямоугольного барьера рис. 6 коэффициент прохождения D ≈
− κa . Отсюда для плавного барьера рис. 8 находим
D ≈
Y
i
− κ x
i
x
i
−
Z
b
a
κ x dx .
Критерий применимости этой формулы обычный:
Z
b
a
|p x |dx h.
36
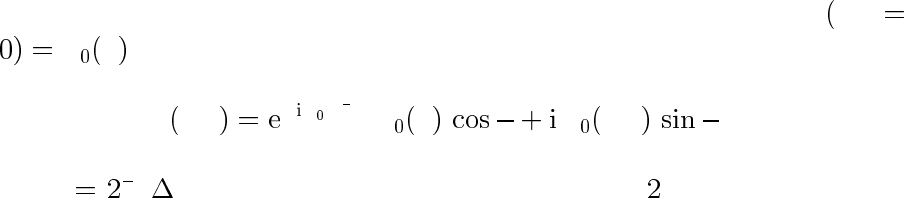
Двойная яма
См. КМ, задача 3 к §50. Дополнительно покажите, что если ψ
x, t
ψ x (частица в начальный момент в правой яме), то
ψ
x, t
−Et/h
"
ψ x
t
τ
ψ−x
t
τ
#
,
где τ
h/ E. Таким образом, через время πτ/ частица окажется
в левой яме, через время πτ — снова в правой яме и т.д.
37
ВОПРОСЫ
12.1. Получить квазиклассическое выражение для уровней энер-
гии частицы в однородном поле тяжести в случае, когда ее дви-
жение ограничено снизу идеально отражающей плоскостью. Ука-
зать условие применимости полученного результата (задачи 9.2 и
9.3 ГКК).
12.2. Задача 2.4 ГКК. Для частицы, находящейся в поле
U
x U|x/a|
ν
U > ,ν>,
найти в квазиклассическом приближении, как изменяется расстоя-
ние между соседними уровнями энергии с увеличением n в зависи-
мости от значения параметра ν. Какова плотность состояний дис-
кретного спектра?
12.3. Найти волновые функции ψ
n
x для гармонического осцил-
лятора при n
.Датьграфик|ψ
n
x|и сравнить его с графиком
классической плотности вероятности
dW
x
dx v x T
,
где T
π/ω — классический период движения. Сравнить так-
же эти величины для состояния n
.
12.4. Вычислить в квазиклассическом приближении коэффици-
ент прохождения электронов через поверхость металла под действи-
ем сильного электрического поля E (“холодная эмиссия”). Найти
границы применимости расчета. Оценить плотность тока через по-
верхность металла при E ∼−
эВ, E∼ В/см.
12.5. Найти расщепление основного состояния в двойной яме.
Потенциал каждой ямы вблизи минимума аппроксимируется осцил-
ляторным, барьер по-прежнему считается квазиклассическим. Срав-
н ит ь о твет ы д л я это й за дач и и д ля за дач и 3 к §50, КМ.
§13. Квазистационарные состояния. α-распад
Возбужденные состояния квантовых систем нестационарны, распа-
даются — элементарное излучение ядер, атомов, молекул, радио-
активный распад ядер и т.д. Закон распада: число распавшихся за
38
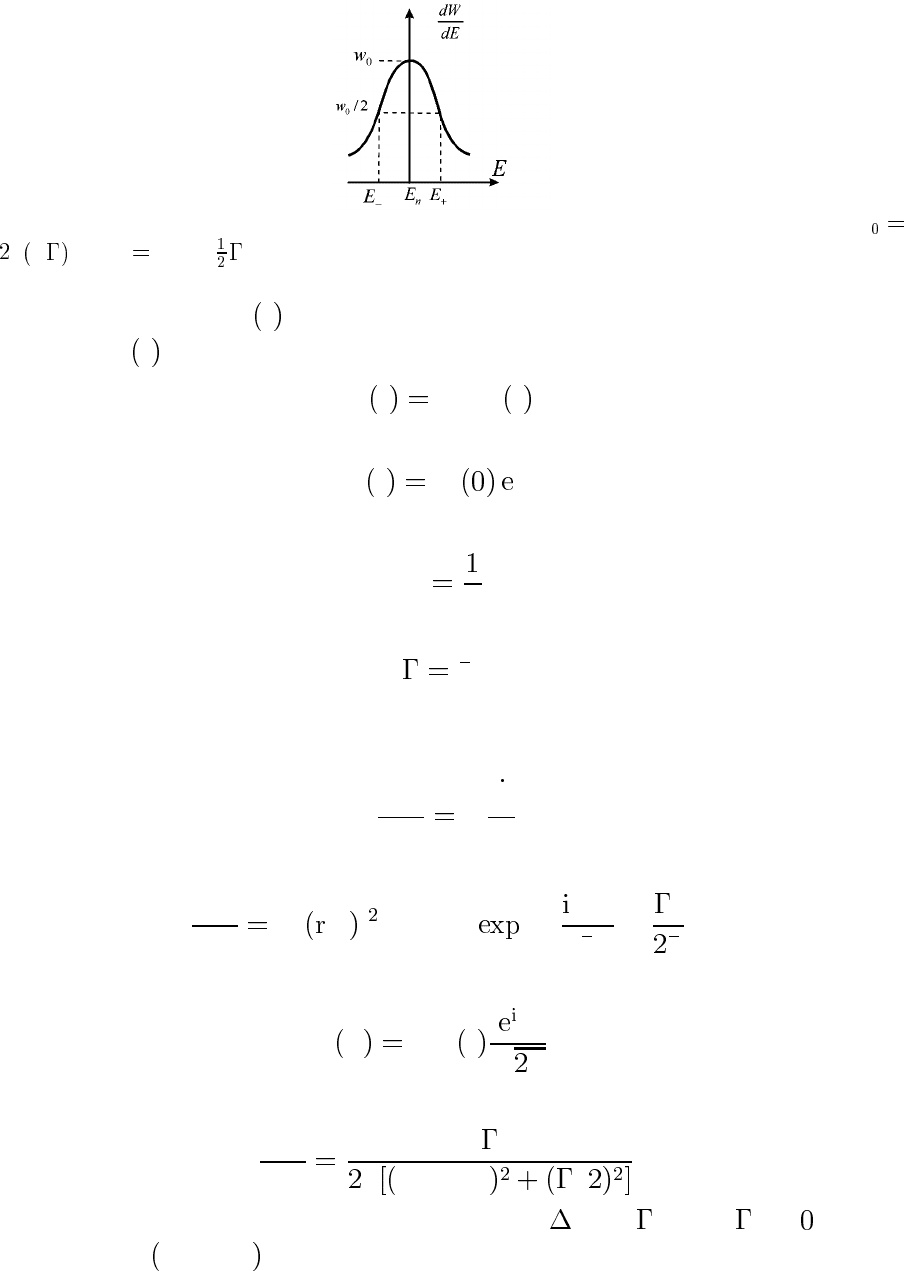
Рис. 9: Распределение по энергии для квазистационарного состояния. Зде сь w
/ π и E
±
E
n
±
время dt частиц dN t пропорционально числу имеющихся в данный
момент N
t и интервалу времени dt,тоесть
dN
t −γN t dt ,
откуда получаем
N
t N
−γt
.
Определения: время жизни
τ
γ
,
ширина квазиуровня
hγ .
Вероятность в единицу времени для каждого атома или ядра остать-
ся в возбужденном состоянии
dW
dt
−
N
N
.
Мод ел ь
dW
dt
|ψ ,t | ,ψ∼
"
−
E
n
t
h
−
t
h
#
.
Вычислив спектральный состав состояния
ψ
ω
Z
ψ t
ωt
√
π
dt ,
получим (см. рис. 9)
dW
dE π E − E
n
/
,
то есть у квазистационарного состояния
E ∼ .При → имеем
dW/dE → δ
E − E
n
и состояние переходит в стационарное.
39
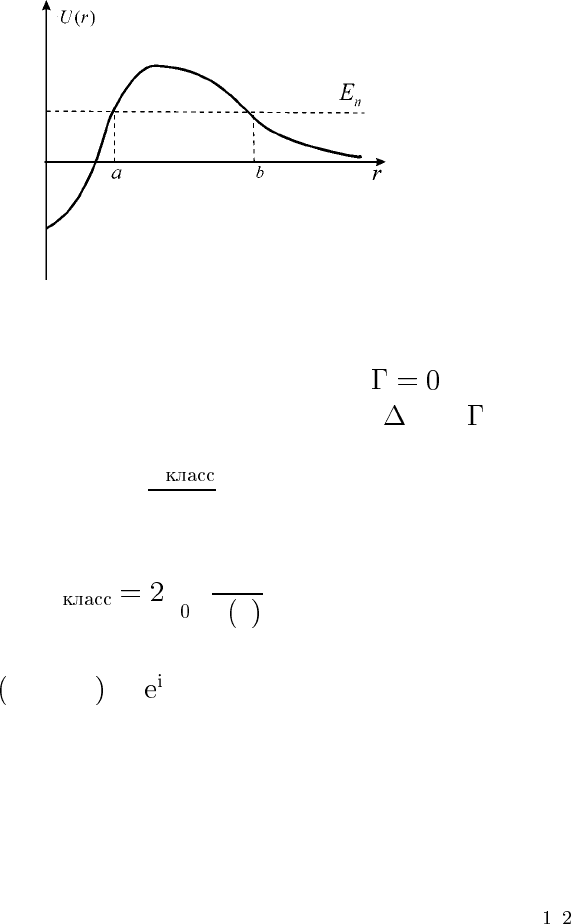
Модель α-распада
Пусть α-частица движется в потенциальном поле вида рис. 10, где
на малых расстояниях действуют притягивающие ядерные силы, а
на больших расстояниях — кулоновское отталкивание. При b →∞
Рис. 10: Потенциа льная энергия, соответст вующ ая случаю α-распада
уровень E
n
— обычное стационарное состояние с .Конечность
барьера приводит к конечному времени жизни τ и
E ∼ . Оценка
τ ∼
T
D
,
где
T
Z
a
dr
v r
.
Постановка задачи с начальным условием. Постановка квазиста-
ционарной задачи с ψ
r →∞ ∝
kr
.
ВОПРОСЫ
13.1. “Пожалуй самым ярким и удивительным свойством α-распада
является очень сильная зависимость периода полураспада T
/
от
энергии вылетающих α-частиц E” (Широков Ю.М., Юдин Н.П. Ядер-
40
