Сербо В.Г., Хриплович И.Б. Конспект лекций по квантовой механике
Подождите немного. Документ загружается.


а действие оператора a на состояние |ni переводит его в состояние
|n −
i, то есть понижает энергию состояния на .Этопозволяет
использовать удобную интерпретацию: состояние |n i содержит n
одинаковых частиц (квантов) с энергией E
(или hω вобычных
единицах) каждая, оператор
a называют повышающим оператором
или оператором рождения такой частицы, а оператор
a — понижа-
ющим оператором или оператором уничтожения. Заметим еще, что
собственные значения оператора
n a a H −
равны n, поэтому n называют оператором числа частиц.
Найдем коэффициент c
n
. Для этого вычислим норму вектора (7.2):
hn|
aa |ni hn|H /|ninc
n
.
Отсюда c
n
√
n . Таким образом, состояние |ni может быть за-
писано так:
|n i
a
n
√
n
|i,
а отличные от нуля матричные элементы операторов рождения и
уничтожения равны
hn
|a|nihn|a|ni
√
n.
Волновая функция основного состояния может быть найдена из
условия
aψ x .
Это дает
ψ
x
−x/
√
π
.
Для волновой функции с n>
получаем компактное выражение
ψ
n
x
a
n
√
n
−x/
√
π
.
ВОПРОСЫ
7.1. Найти ϕ
n
p для линейного осциллятора.
21
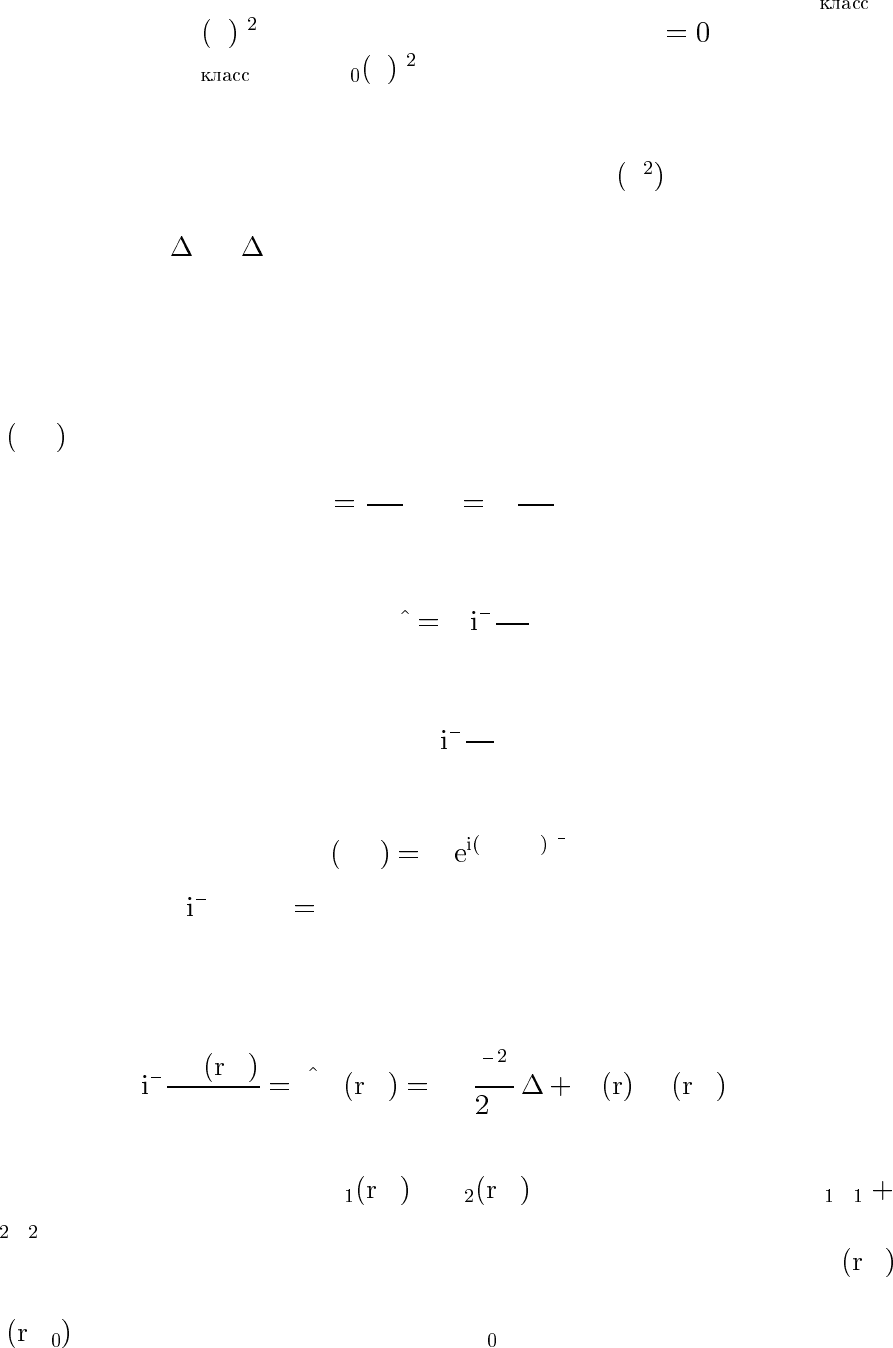
7.2. Для линейного осциллятора сравнить классическуюdW /dx
и квантовую |ψ
n
x | плотности вероятности при n .
То же дл я dW
/dp и |ϕ p | .
Найти вероятность того, что в основном состоянии осциллятор
находится в классичечки недоступной области |x| >`.
7.3. Найти матричные элементы x
fi
,p
fi
, x
fi
для линейного
осциллятора.
7.4. Найти
x и p для линейного осциллятора в n-м состоянии.
§8. Временн
´
ое уравнение Шредингера
В классической механике импульс и энергия связаны с действием
S
x, t соотношениями
p
∂S
∂x
,E
−
∂S
∂t
.
Если в квантовой механике
p →
p − h
∂
∂x
,
то естественно ожидать, что
E →
h
∂
∂t
.
Проверим, что для плоской волны
ψ
x, t A
px−Et /h
это так и есть: h∂ψ/∂t Eψ.
Конечно, всe это лишь наводящие соображения, показывающие
естественность следующего утверждения: в квантовой механике по-
стулируется УШ в виде
h
∂ψ
,t
∂t
Hψ ,t
−
h
m
U
ψ ,t .
Его свойства:
1. УШ линейно: если ψ
,t и ψ ,t — решения УШ, то c ψ
c ψ также является решением УШ (принцип суперпозиции).
2. УШ имеет первый порядок по времени, поэтому значения ψ
,t
в любой момент времени полностью определяется, если известна
ψ
,t в некоторый момент времени t .
22
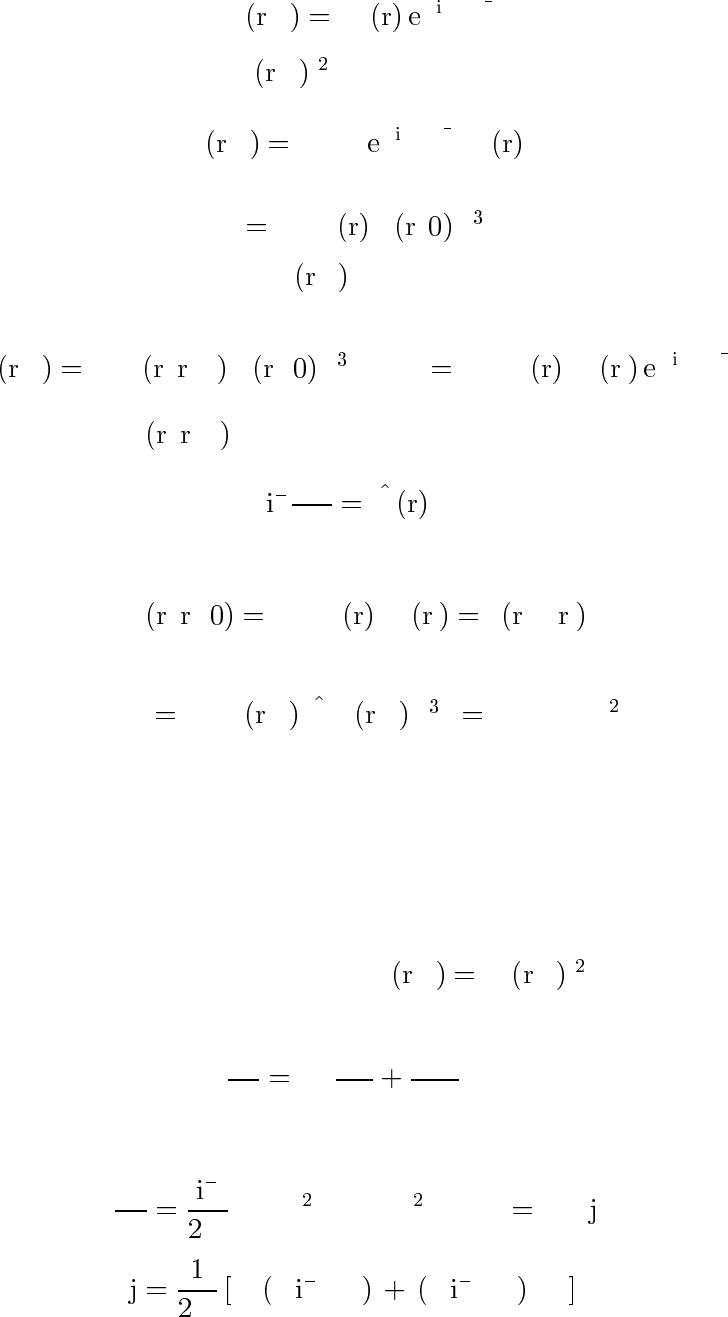
Для стационарного решения
ψ
,t ψ
n
− E
n
t/h
плотность вероятности |ψ ,t | не зависит от t. Общее решение та-
ково
ψ
,t
X
n
c
n
−E
n
t/h
ψ
n
,
где
c
n
Z
ψ
∗
n
ψ , d r.
Таким образом, эволюция ψ
,t с течением времени описывается
уравнением
ψ
,t
Z
G,
0
,t ψ
0
, d r
0
,G
X
n
ψ
n
ψ
∗
n
0 −E
n
t/h
.
Функция Грина G
,
0
,t удовлетворяет уравнению
h
∂G
∂t
H G
с начальным условием
G
,
0
,
X
n
ψ
n
ψ
∗
n
0
δ −
0
.
Из
hEi
Z
ψ
∗
,t Hψ ,t d r
X
n
E
n
|c
n
|
видно, что c
n
есть амплитуда вероятности обнаружить у системы
энергию E
n
.Наборвеличинc
n
есть волновая функция системы в
энергетическом представлении.
Плотность тока
Изменение плотности вероятности %
,t |ψ,t | со в р ем е н ем оп ре-
деляется уравнением
∂%
∂t
ψ
∗
∂ψ
∂t
∂ψ
∗
∂t
ψ.
Подставив ∂ψ/∂t из УШ, получим уравнение непрерывности
∂%
∂t
h
m
h
ψ
∗
∇ ψ −
∇ ψ
∗
ψ
i
−∇ ,
m
ψ
∗
− h∇ψ − h∇ψ
∗
ψ .
23
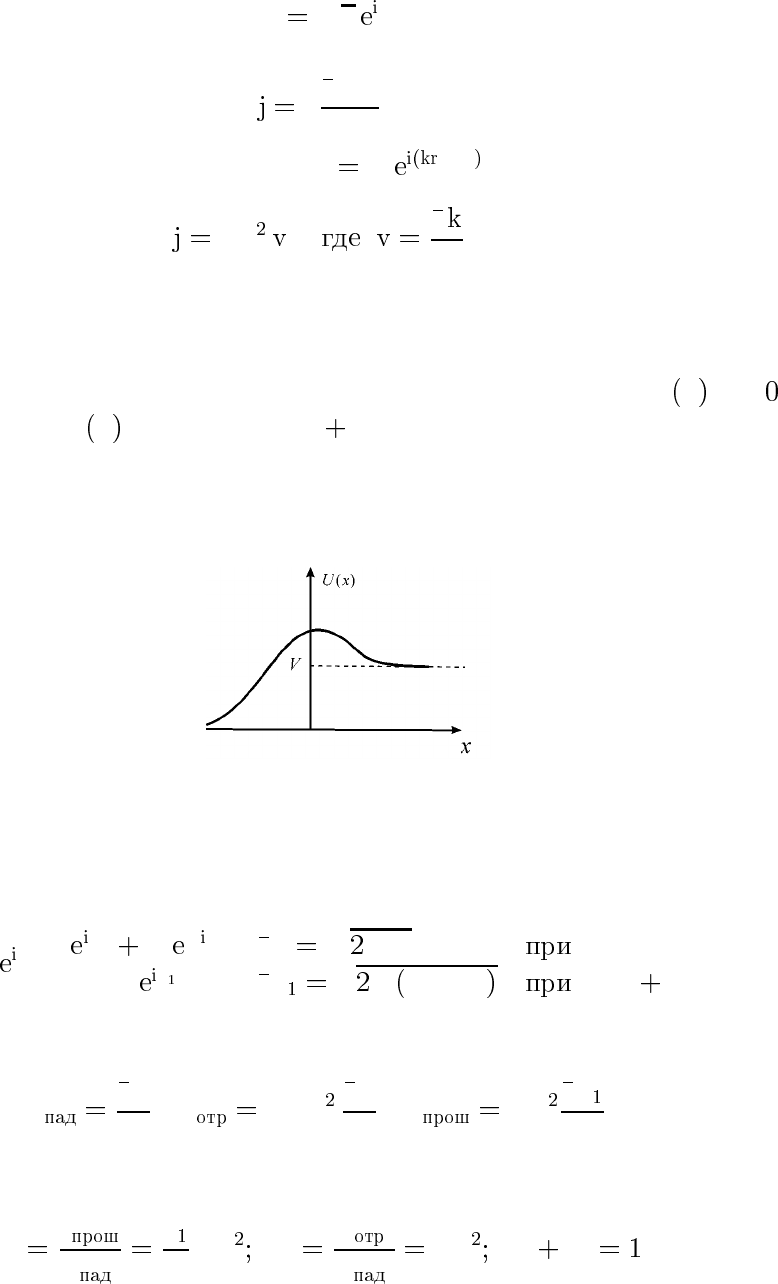
Для
ψ
√
%
φ
имеем
%
h∇φ
m
.
В частности, для плоской волны ψ
A
−ωt
плотность тока равна
|A| ,
h
m
.
§9. Одномерное рассеяние
Для потенциальной энергии указанного на рис. 2 вида (U x →
при x →−∞,U x →V при x → ∞) задача рассеяния при E>V
Рис. 2: Потенциа ль ная э нергия для случая одноме рно го расс еяния
формулируется так. Слева имеется падающая и отраженная волна,
справа — прошедшая. Асимптотики волновой функции таковы:
ψ →
ωt
kx
A
− kx
, hk
√
mE x →−∞
B
k x
, hk
q
m E − V x → ∞.
Плотности x-компонент тока равны:
j
hk
m
,j
−|A|
hk
m
,j
|B|
hk
m
.
Коэффициенты прохождения D и отражения R равны:
D
j
j
k
k
|B|
R
|j |
j
|A| R D .
24
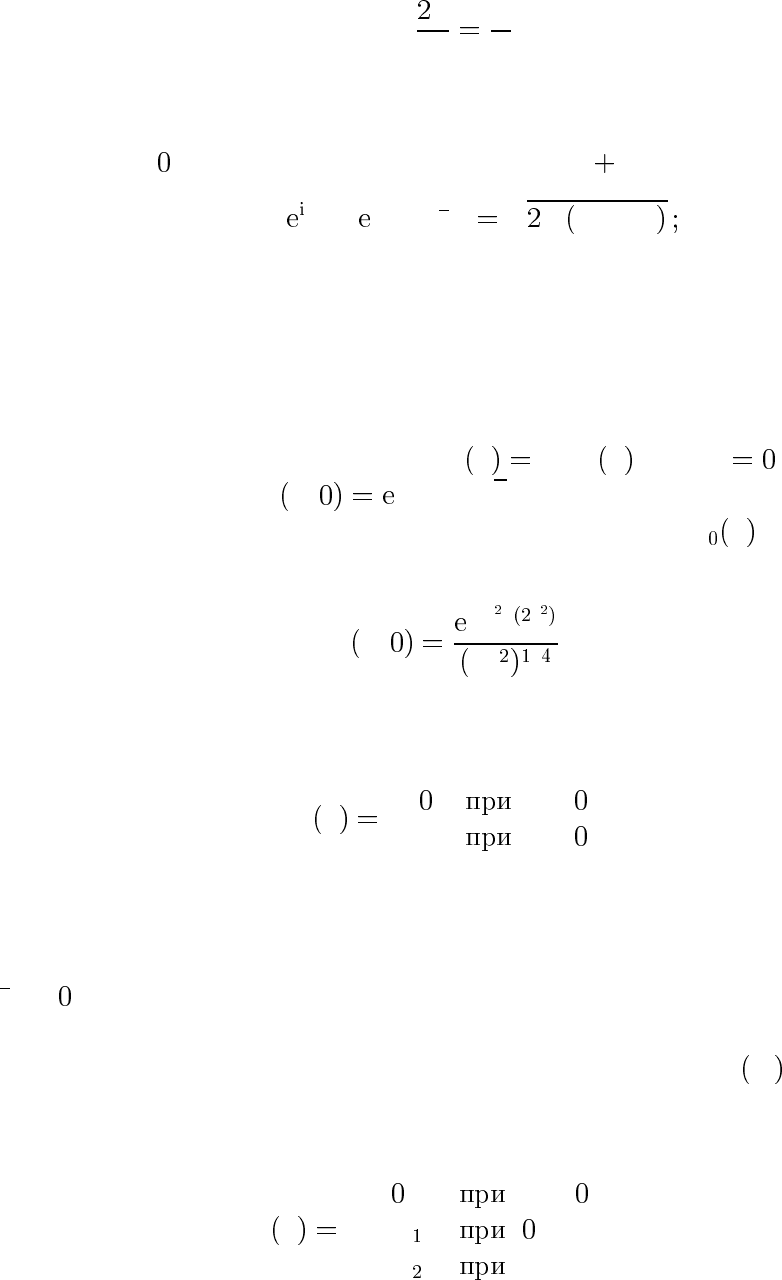
Оптический аналог — отражение света при нормальном падении
на плоскую границу раздела двух сред. В оптике волновой вектор
k ≡
π
λ
ω
c
n,
где n — показатель преломления. Здесь нашей задаче соответствует
ситуация, когда справа — вакуум, а слева — стекло.
Вслучае
<E<V асимптотика при x → ∞ изменяется,
ψ →
ωt
B
−κx
, hκ
q
m V − E
Здесь оптический аналог — полное внутреннее отражение.
ВОПРОСЫ
9.1. Частица находится в поле U
x −Gδ x .Приt вол но в ая
функция имеет вид ψ
x,
−|x|/b
/
√
b. Найти вероятность того, что
при t →∞частица окажется в основном состоянии ψ
x .
9.2. Тот же вопрос для гармонического осциллятора при
ψ
x,
−x / b
πb
/
.
9.3. Найти функцию Грина для свободной частицы.
9.4. Найти D и R для частицы в поле рис. 3
U
x
x<
V x> .
Указать оптическую аналогию. Известно, что при отражении от
оптически более плотной среды происходит потеря полуволны. Че-
му соответствует это явление в данной задаче? Рассмотреть предел
h → .
9.5. Найти D для частицы в поле прямоугольной потенциальной
ямы глубины V и ширины a (рис. 4). Дать график D
E , указать
условие прозрачности. Указать необходимое условие прозрачности
вслучаеполярис.5:
U
x
x<
−V <x<a
−V
x>a,
25
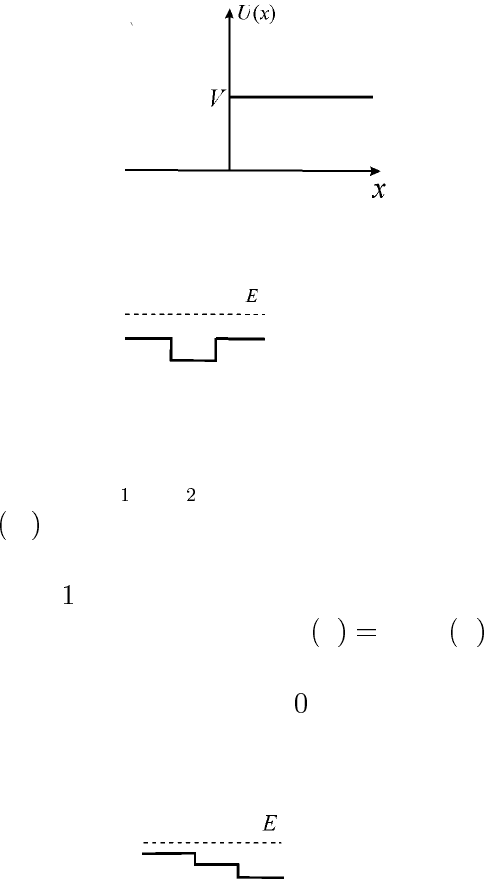
Рис. 3 : Потенциальная “ступенька”
Рис. 4 : Прохождение частицы над одномерно й прямоугольной ямой
соответствующего при V <V просветленной оптике.
9.6. Найти D
E для частицы в поле прямоугольного потенциаль-
ного барьера высотою V и шириною a (рис. 6), особо рассмотреть
случай E<V,κa
.
9.7. Рассмотреть рассеяние в поле U
x −Gδ x . Обратить вни-
мание на поведение амплитуд отраженной и прошедшей волн при
продолжении решения в область E<
.
Рис. 5: Потенци альная энергия, соответствующая случаю просветленной опти-
ки
26
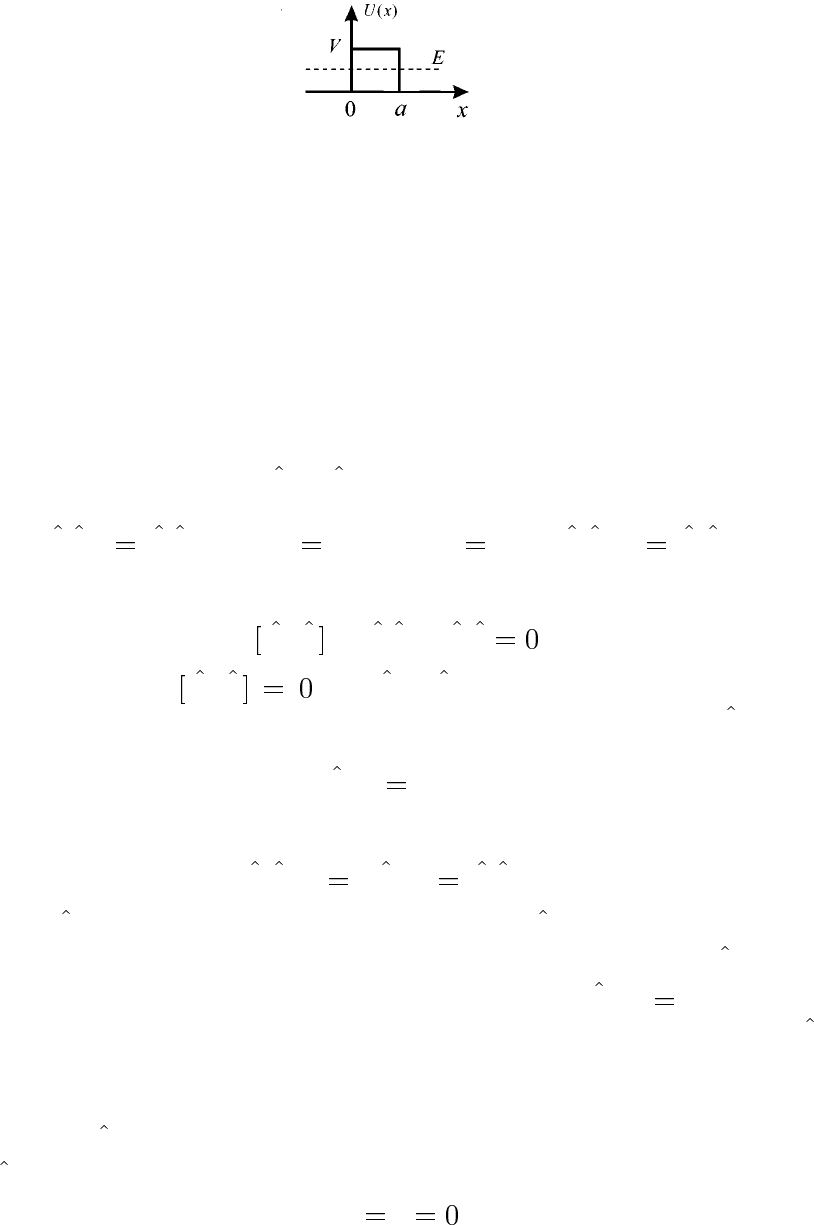
Рис. 6 : Туннелирование частицы через одномерный прямоугольный барьер
§10. Коммутаторы.
Снова соотношение неопределенностей.
Уравнение Эренфеста. Теорема о вириале
Измеримость величин
Если величины A и B одновременно измеримы, то существует пол-
ная система волновых функций ψ
n
,таких,чтоψ
n
— одновременно
собственная функция и
A,иB.Нотогда
ABψ AB
X
n
c
n
ψ
n
X
n
c
n
ab ψ
n
X
n
c
n
BAψ
n
BAψ,
то есть
A, B ≡ AB − BA .
И обратно, если
A, B ,тоAиBмогут иметь общую систему
собственных функций. Пусть ψ
a
— собственная функция A:
Aψ
a
aψ
a
,
тогда
BAψ
a
aBψ
a
ABψ
a
,
то есть
Bψ
a
— тоже собственная функция A с собственным значе-
нием a. Если спектр невырожден, отсюда следует, что
Bψ
a
сточ-
ностью до множителя совпадает с ψ
a
,тоестьBψ
a
bψ
a
,такчто
ψ
a
, действительно, является собственной функцией оператора B (с
собственным значением b). В случае вырожденного спектра можно
выбрать такие линейные комбинации
P
i
c
i
ψ
ai
собственных функций
оператора
A, которые будут одновременно собственными функция-
ми
B.
Рассмотрите также случай a
b .
27
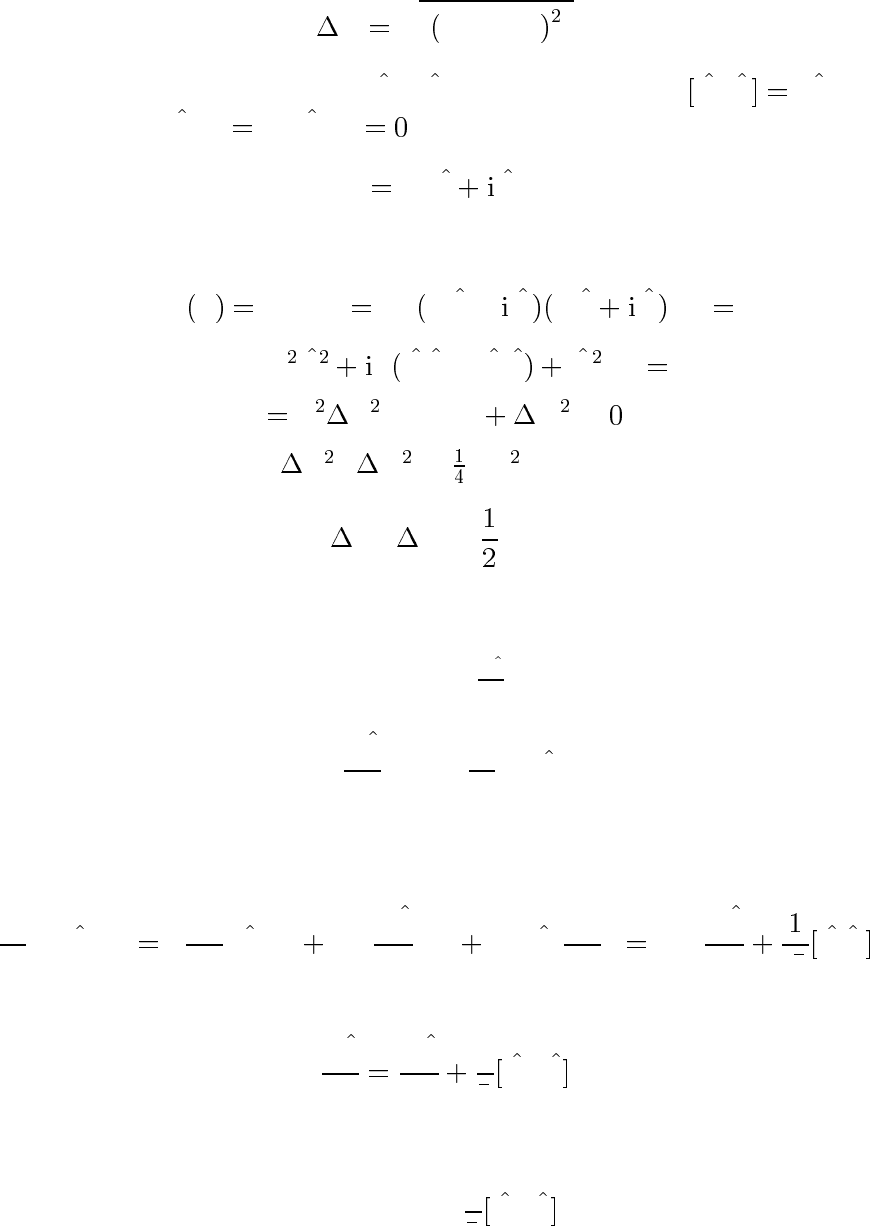
Соотношение неопределенностей
Определим дисперсию
A
r
h A −hAi i.
Пусть эрмитовы операторы
A и B не коммутируют, A, B iCидля
простоты hn|
A|ni hn|B|ni . Рассмотрим состояние
|mi
αA B
|ni.
Ясно, что
J
α hm|mihn|αA−BαA B|ni
hn|αAαAB−BAB|ni
αA−αhCiB≥.
Отсюда следует , что
A · B ≥ hCi . Так им об ра з ом,
A · B ≥ |hCi|.
Квантовые скобки Пуассона
Оператор производной по времени
dA
dt
, по определению, удовлетво-
ряет ус ло ви ю
*
ψ
dA
dt
ψ
+
≡
d
dt
hψ|
A|ψi.
Используя УШ, правую часть этого равенства можно переписать в
виде
d
dt
hψ|
A|ψi
*
∂ψ
∂t
A
ψ
+ *
ψ
∂A
∂t
ψ
+ *
ψ
A
∂ψ
∂t
+ *
ψ
∂A
∂t ih
AH
ψ
+
.
Та ки м об ра з ом,
d
A
dt
∂A
∂t
i
h
H,A .
Квантовый аналог скобки Пуассона {H, A} выражается через ком-
мутатор:
{H, A}→
i
h
H,A .
28
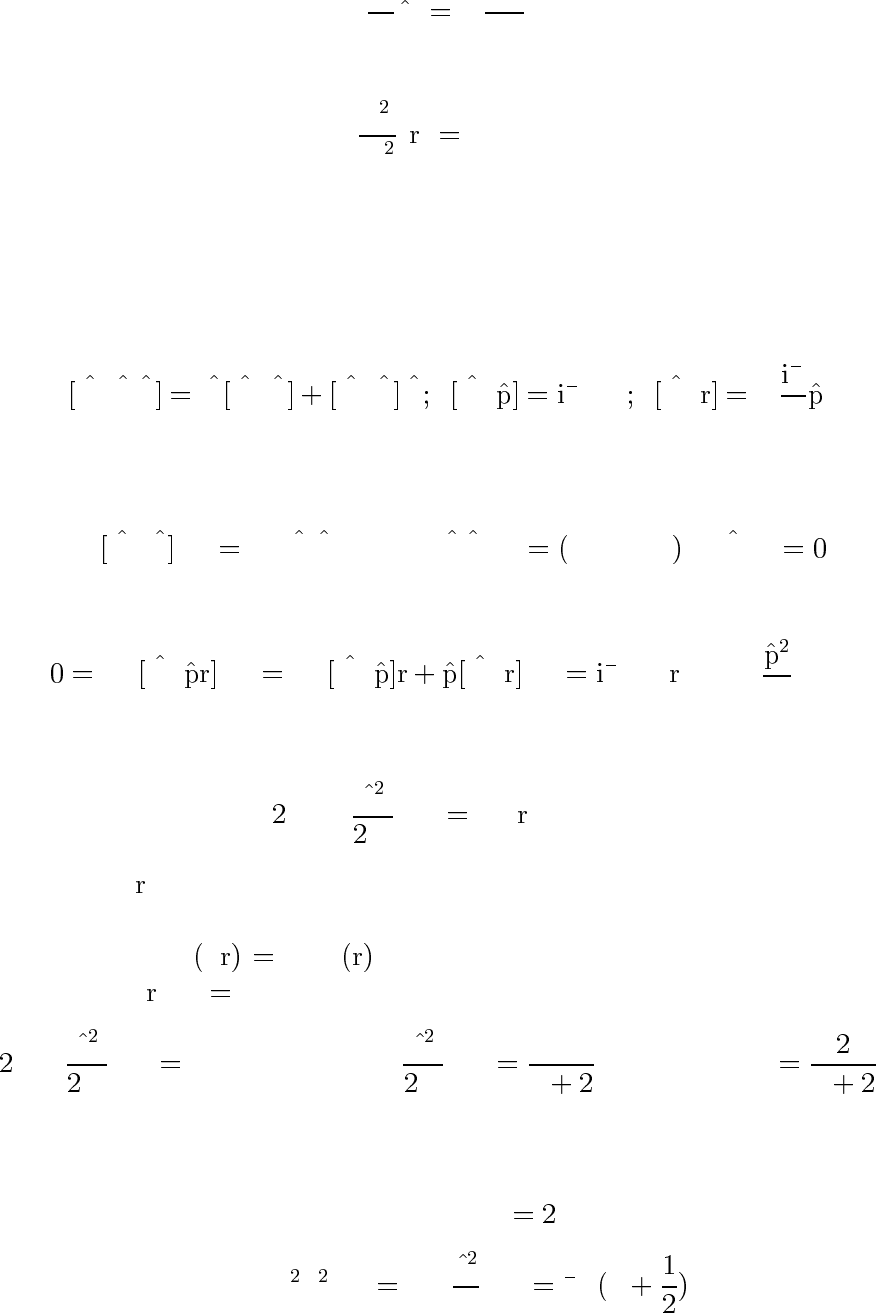
По ка жи те, ч то
d
dt
p
x
−
∂U
∂x
.
Отсюда следует теорема Эренфеста
m
d
dt
h i −h∇Ui.
Обсудите еe сооотношение со вторым законом Ньютона.
Теорема о вириале
Предварительные полезные соотношения:
A, BC BA, C A, B C H, h∇U H, −
h
m
.
Пусть |ni — стационарное состояние дискретного спектра (фи-
нитное движение), тогда
hn|
H,A |ni hn|HA|ni−hn|AH|ni E
n
−E
n
hn|A|ni .
В частности,
hn| H, |ni hn| H, H, |ni h
*
n
∇U −
m
n
+
.
Таким ообразом,
·
*
n
p
m
n
+
hn| ∇U|ni .
Величина
∇U называется вириалом данной механической системы.
Если потенциальная энергия — однородная функция координат,
то ес ть ес ли U
λ λ
k
U , то, по теореме Эйлера об однородных
функциях,
∇U kU,или
·
*
n
p
m
n
+
khn|U|ni,
*
n
p
m
n
+
k
k
E
n
,hn|U|ni
k
E
n
.
Примеры
Для гармонического осциллятора k
, п оэтом у
D
n
mω x
n
E
*
n
p
m
n
+
hω n .
29
Для атома водорода k − , п оэтом у
*
n
e
r
n
+ *
n
m
n
+
− E
n
. .
ВОПРОСЫ
10.1. Объясните, почему теорема о вириале не имеет места для
инфинитного движения.
10.2. Найти соотношение неопределенностей для
x и K,для
Uи K,гдеK p/ m .
10.3. Для частицы, находящейся в состоянии ψ
x, y, z ,найтиве-
роятность того, что ее координата x иимпульсp
y
расположены в
п р ед ел а х x
<x<x,p
y
<p
y
<p
y
.
10.4. Для гамильтониана
H / m Uнайти коммутатор
H, . Используя этот результат, показать, что среднее значение им-
пульса частицы для стационарного состояния в случае финитного
движения равно нулю hψ
E
| |ψ
E
i .
§11. Оператор сдвига. Теорема Блоха
Оператор сдвига T
a
определяется соотношением
T
a
ψ x ≡ ψ x a .
Та к как
ψ
x a
∞
X
n
a
n
n
d
dx
!
n
ψ x ,
то оператор сдвига может быть выражен через оператор импульса
T
a
ap/h
.
Обратим внимание на то, что при бесконечно малом сдвиге δa →
оператор сдвига имеет вид
T
δa
δa
h
p,
то есть оператор импульса
p
x
является инфинитезимальным опера-
тором для сдвига вдоль оси x.
30
