Сербо В.Г., Хриплович И.Б. Конспект лекций по квантовой механике
Подождите немного. Документ загружается.

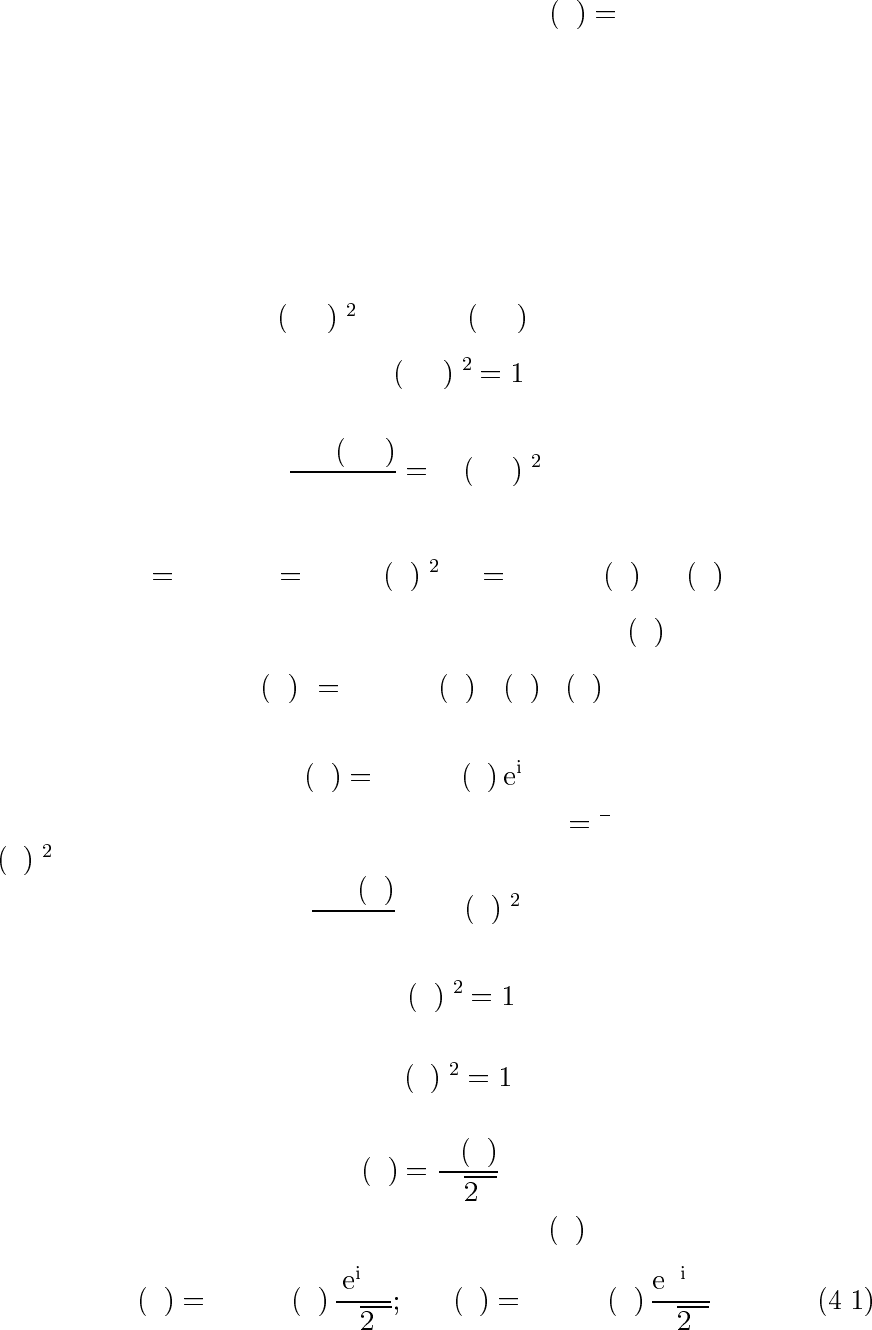
3.6. Используя соотношение неопределенностей, оценить энер-
гию основного состояния частицы в поле U
x α|x|.
3.7. Используя соотношение неопределенностей, оценить глуби-
ну уровня в одномерной мелкой яме.
§4. Координатное и импульсное представления.
Операторы физических величин
Плотность вероятности найти частицу в точке x — величина dW/dx
— пропорциональна |ψ
x, t | . Если ψ x, t нормирована условием
Z
dx|ψ x, t | ,
то
dW
x, t
dx
|ψ x, t | .
Тогда среднее значение x равно
hxi
Z
xdW
Z
x|ψ x | dx
Z
dx ψ
∗
x xψ x .
Аналогично, среднее значение любой функции F
x равняется
hF
x i
Z
dx ψ
∗
x F x ψ x .
Если
ψ
x
Z
dk A k
kx
,
то вероятность найти частицу с импульсом p
hk пропорциональна
|A
k | ,или
dW
k
dk
∝|A
k | .
Если
Z
dx |ψ x | ,
то и
Z
dk |ϕ k | .
Здесь
ϕ
k
Ak
√
π
— нормированный Фурье-образ функции ψ
x ,тоесть
ψ
x
Z
dk ϕ k
kx
√
π
ϕ k
Z
dx ψ x
− kx
√
π
.
.
11

По этом у
dW
dk
|ϕ k |
и
hF
k i
Z
dk ϕ
∗
k F k ϕ k .
Выразим hpi через ψ
x . Подставляя в соотношение
hpi
Z
dk ϕ
∗
k hk ϕ k
выражение ϕ k через ψ x из (4.1), получим
hpi
Z
dk
Z
dx
0
ψ
∗
x
0
kx
0
√
π
hk
Z
dxψ x
− kx
√
π
.
Используя тождество
k
− kx
d
dx
− kx
и интегрируя по x по частям, получим окончательно
hpi
Z
dxψ
∗
x
− h
d
dx
!
ψ x .
Здесь при интегрировании по k использована известная формула
Z
dk
k x
0
−x
πδ x
0
−x .
Таким образом, при нахождении hpi можно пользоваться формулой
hpi
Z
dx ψ
∗
x pψ x ,
где оператор
p − h
d
dx
.
.
В квантовой механике постулируется, что динамические пере-
менные описываются операторами, так что среднее значение не-
которой переменной A в состоянии с заданной волновой функцией
ψ
x (или ϕ p )равно
hAi
Z
dx ψ
∗
x Aψ x
Z
dp ϕ
∗
p Aϕ p .
В частности, оператор импульса в x-пространстве определяется фор-
мулой (4.2), а в p-пространстве — это просто оператор умножения
p p. Аналогично, оператор x x в x-пространстве и
x h
d
dp
12
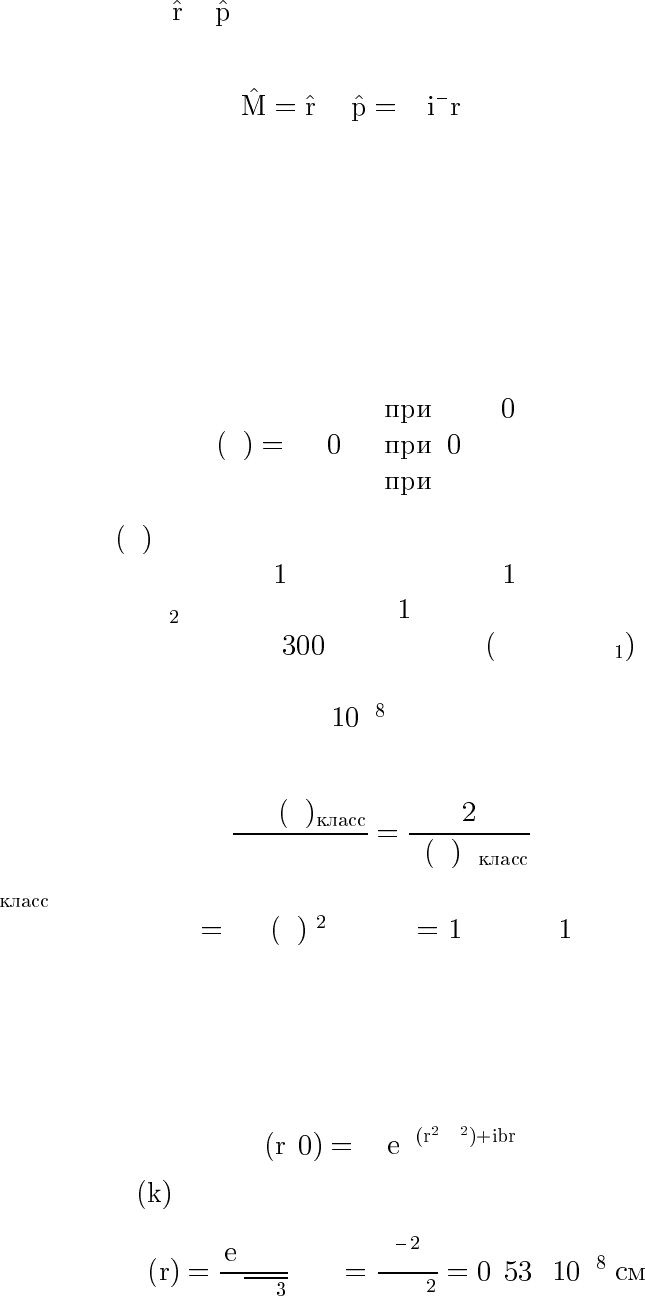
в p-пространстве.
Из операторов
и строятся все динамические переменные. На-
пример, оператор момента импульса
×−h ×∇.
ВОПРОСЫ
4.1. Для потенциального ящика вида
U
x
∞x<
<x<a
∞
x>a
найти E
n
и ψ
n
x . Оценить E
n
для
а) частицы массы m ∼
г в ящике с a ∼ см;
б) молекулы H
в ящике с a ∼ см; найти n, соответствующий
энергии E
n
∼ kT ,гдеT ∼ К; оценить E
n
−E
n−
/E
n
для данной
энергии;
в) электрона в ящике с a ∼
−
см.
Сравнить классическую плотность вероятности, определенную
соотношением
dW
x
dx v x T
,
где T
— классический период колебаний, и квантовую плотность
вероятности dW/dx
|ψ
n
x | при n и n . Провести такое же
сравнение для dW/dp — плотности вероятности в импульсном про-
странстве.
4.2. Найти изменение с течением времени волновой функции не-
релятивистской свободной частицы массы m,есливначальныймо-
мент времени
ψ
, A
− /a
.
4.3. Найти ϕ
для
ψ
−r/a
√
πa
,a
h
m
e
e
, ·
−
13
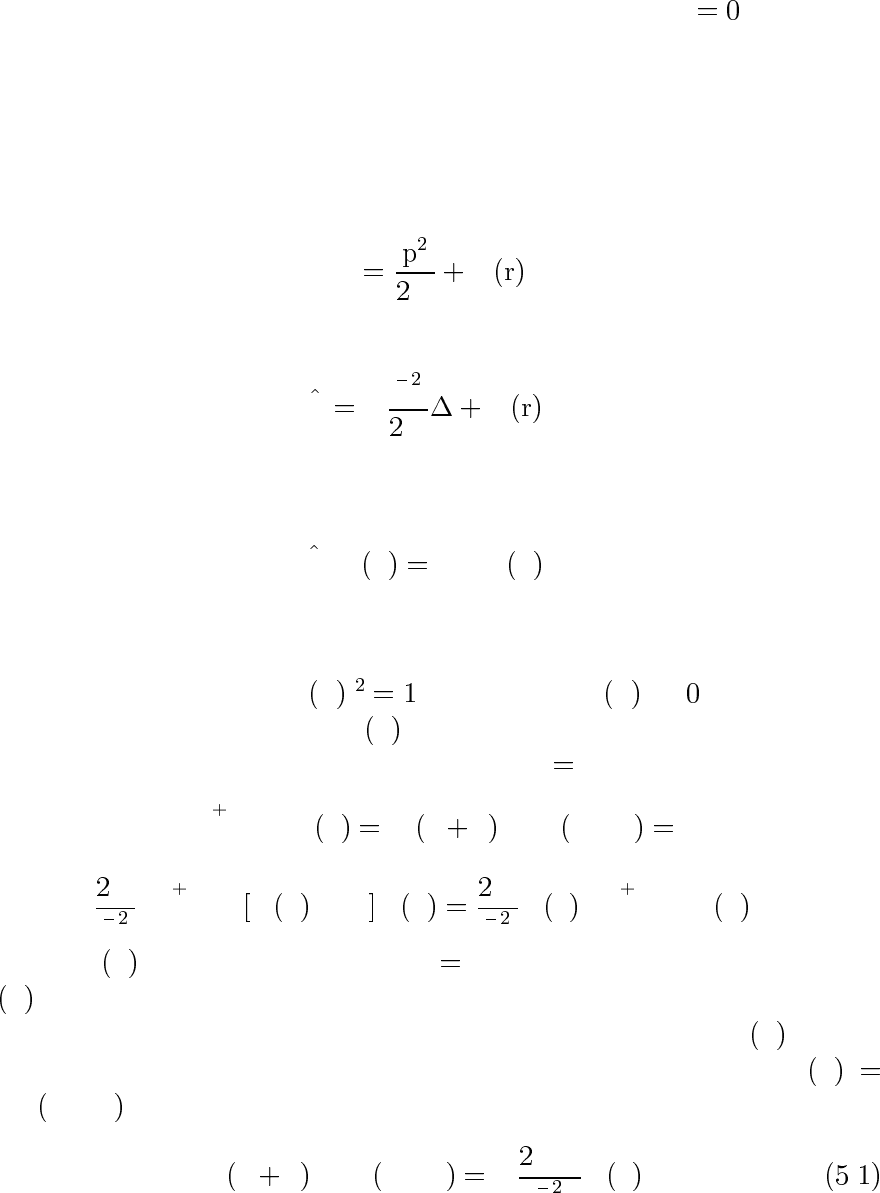
(основное состояние атома водорода). Пусть данная волновая функ-
ция описывает состояние свободного электрона при t
. Оценить,
на каком расстоянии окажется этот электрон через 1 с.
§5. Оператор Гамильтона. Уравнение Шр
¨
едингера
Классическая функция Гамильтона
H
m
U
заменяется оператором Гамильтона
H −
h
m
U.
Собственная функция этого оператора с собственным значением E
n
удовлетворяет уравнению Шредингера (УШ) (1925 г.)
Hψ
n
x E
n
ψ
n
x.
Решения этого уравнениея ищутся в классе однозначных и непре-
рывных функций. В случае связанных состояний эти функции нор-
мируемы (для них
R
dx|ψ
n
x | ) и п оэтом у ψ
n
x → при x →±∞.
Поведение производной ψ
0
x определяется видом потенциала. Ин-
тегрируя УШ в малой окрестности точки x
a,получаем
Z
a
ε
a−ε
dx ψ
00
x ψ
0
aε−ψ
0
a−ε
m
h
Z
a
ε
a−ε
dx U x − E ψ x
m
h
ψa
Z
a
ε
a−ε
dx U x ,
то ес т ь ψ
0
x непрерывна в точке x a, если потенциальная энергия
U
x непрерывна в этой точке или имеет разрыв 1-го рода (конечный
скачок). У потенциалов, имеющих скачки 2-го рода, ψ
0
x может
иметь разрывы (см. пример потенциального ящика). Для U
x
−Gδ x−a имеем
ψ
0
a ε −ψ
0
a −ε −
mG
h
ψ a . .
Дискретные уровни в одномерной задаче всегда невырожде-
ны, то есть каждому собственному значению энергии соответству-
ет единственная собственная функция. Допустим обратное: пусть
14
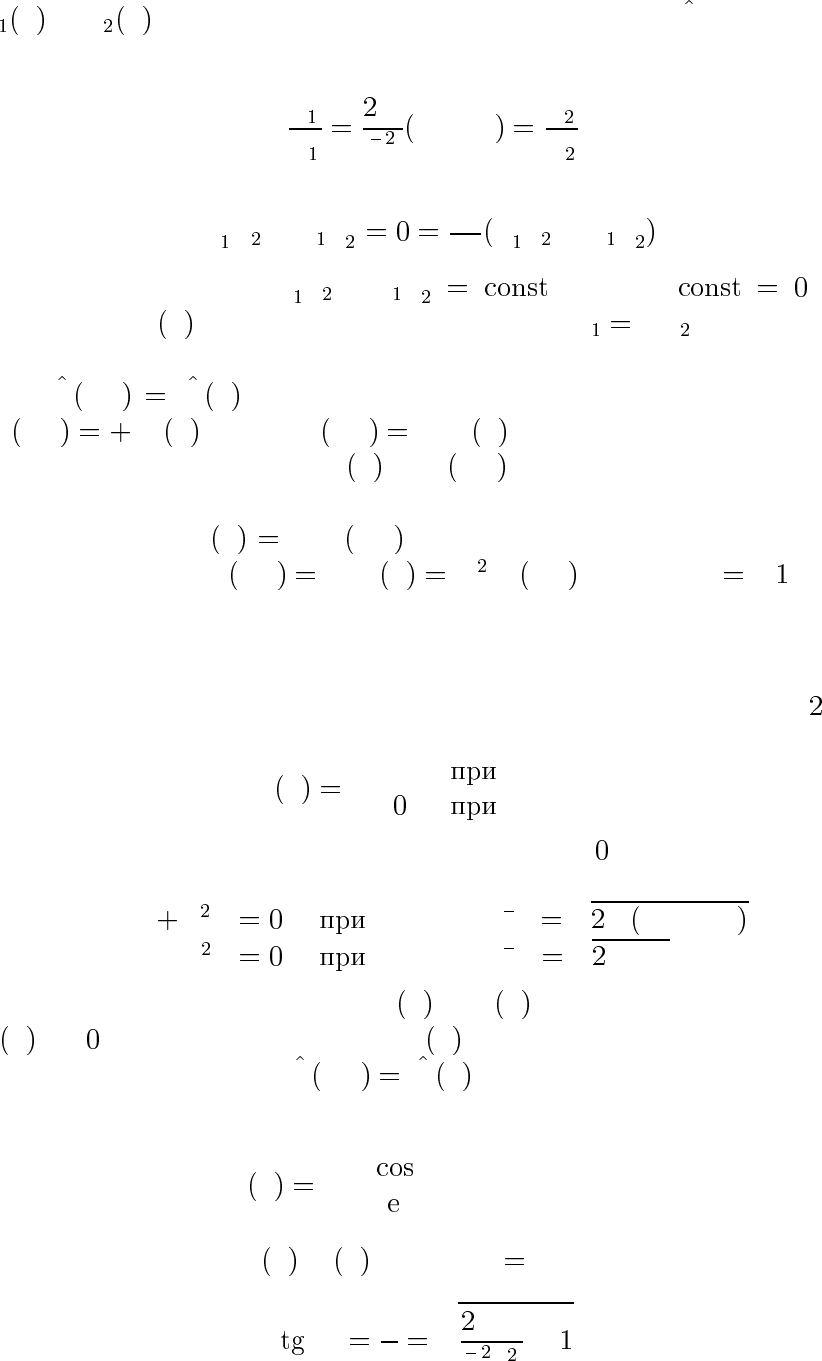
ψ x и ψ x — две разные собственные функции H, отвечающие
одному значению E.Тогда
ψ
00
ψ
m
h
U − E
ψ
00
ψ
или
ψ
00
ψ − ψ ψ
00
d
dx
ψ
0
ψ − ψ ψ
0
.
Отсюда следует , что ψ
0
ψ − ψ ψ
0
. Далее, из-за
поведения ψ
n
x на бесконечности. В итоге, ψ Cψ .
В одномерной задаче дискретные уровни четного гамильтони-
ана,
H −x H x , имеют определенную четность,тоестьлибо
ψ
n
−x ψ
n
x,либоψ
n
−x −ψ
n
x. Действительно, для такого
гамильтониана функции ψ
n
x и ψ
n
−x являются решениями, отве-
чающими одному и тому же значению E
n
, то есть, по предыдущему
утверждению, ψ
n
x Cψ
n
−x . Сделав еще одно отражение коор-
динат, получим ψ
n
−x Cψ
n
x Cψ
n
−x,откудаC ± .
Пример
Прямоугольная потенциальная яма глубиною V и шириною
a,то
ест ь
U
x
−V|x| <a
|x| >a.
Связанным состояниям отвечает энергия E<
, п ри этом У Ш и м еет
вид
ψ
00
k ψ |x| <a, hk
q
m V −|E|
ψ
00
− κ ψ |x| >a, hκ
q
m|E|.
Ищем решения такие, чтобы ψ
x и ψ
0
x были непрерывны, чтобы
ψ
x → при x →±∞ичтобыψx была либо четной, либо нечет-
ной функцией, так как
H −x Hx.
Четные решения имеют вид
ψ
x
Akx при |x| <a,
B
−κ|x|
при |x| >a
Из непрерывности ψ
0
x /ψ x вточкеx aполучаем уравнение
ka
κ
k
v
u
u
t
mV
h k
− ,
15
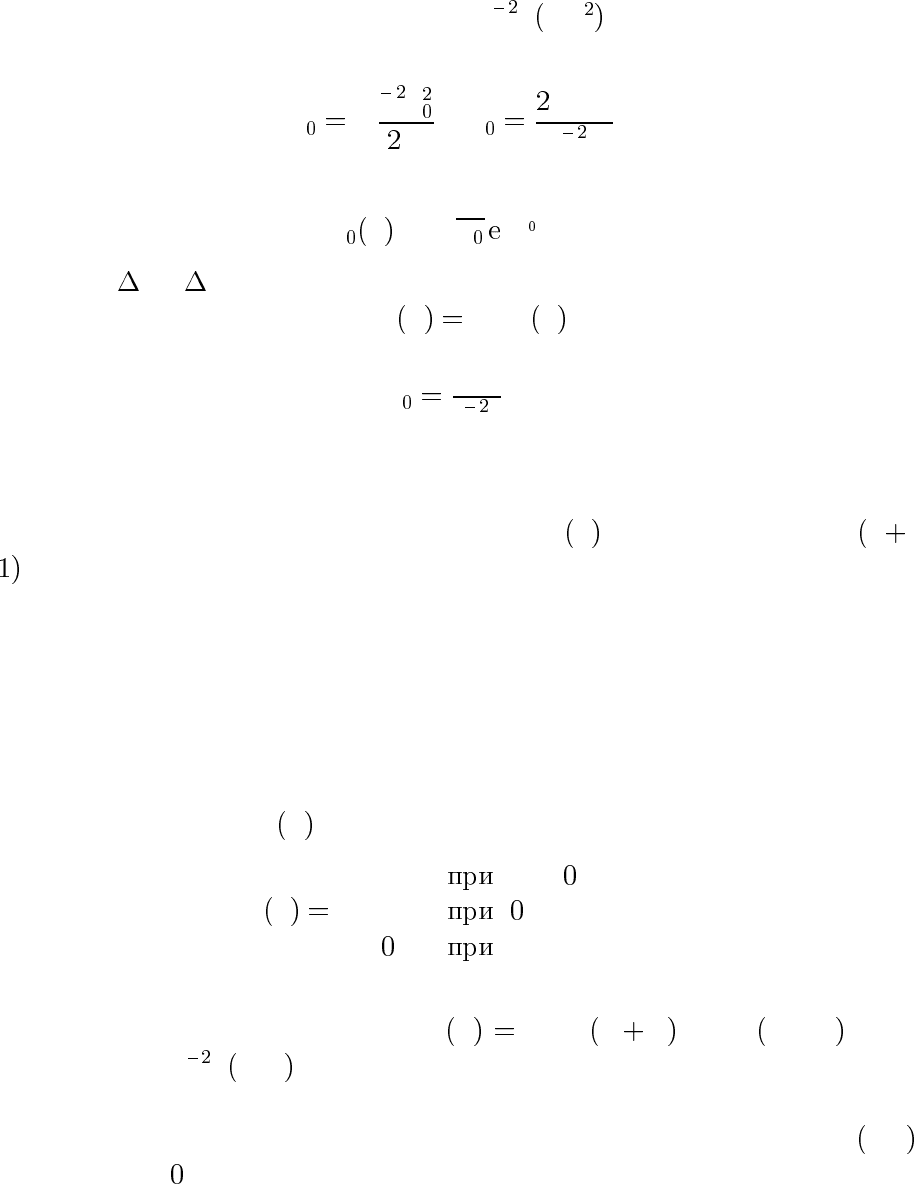
дающее дискретный ряд значений k
n
или E
n
(энергия квантуется).
Найдите нечетные решения и покажите, что четные и нечетные
уровни чередуются.
По ка жи те, ч то в м елкой я ме , V
h / ma , существует лишь од-
но связанное состояние с энергией
E
−
h κ
m
,κ
aV m
h
и волновой функцией
ψ
x ≈
√
κ
−κ |x|
.
Оцените
x и p для такой ямы. Покажите, используя условие (5.1),
что потенциальной энергии U
x −Gδ x соотвествует мелкая яма
с
κ
mG
h
.
Осцилляционная теорема
Волновая функция дискретного спектра ψ
n
x , соответствующая n
-му по величине собственному значению E
n
, обращается в нуль
(при конечных x) n раз (см. примеры потенциального ящика, ос-
циллятора и т.д.).
ВОПРОСЫ:
5.1. Найти E
n
и ψ
n
x для поля
U
x
∞x<
−V <x<a
x>a
.
5.2. Найти уровни энергии и волновые функции связанных состо-
яний частицы в поле двух δ-ям U
x −Gδ x a −Gδ x−a при
условии a
h / mG . Исследовать зависимость уровней энергии
от a.
5.3. Для поля, описанного в предыдущей задаче, определитьψ
x, t ,
есл и пр и t<
между ямами была непроницаемая перегородка и ча-
стица находилась в стационарном связанном состоянии вблизи ле-
во й я м ы.
16

§6. Эрмитовы операторы
Назовем оператор B эрмитово сопряженным коператоруA,если
для любых двух функций ψ
и ψ справедливо соотношение
Z
dx ψ
∗
Aψ
Z
dx Bψ
∗
ψ .
Такой оператор обозначим
B A . Если A A ,тоестьопера-
тор совпадает со своим эрмитово сопряженным, назовем его эрми-
товы м (или самосопряженным). Для эрмитова оператора
Z
dx ψ
∗
Aψ
Z
dx Aψ
∗
ψ .
Собственные значения эрмитова оператора вещественны:
Aψ
λ
λψ
λ
,
Z
dx ψ
∗
λ
Aψ
λ
Z
dx Aψ
λ
∗
ψ
λ
.
Отсюда следует , что λ
λ
∗
.
Аналогично показывается, что среднее значение эрмитова опера-
тора
R
dx ψ
∗
Aψв каком-либо квантовом состоянии ψ – вещественное
число. Все операторы физических величин эрмитовы.
Собственные функции, отвечающие различным собственным зна-
чениям эрмитова оператора, взаимно ортогональны. Действитель-
но, домножив
Aψ
λ
λψ
λ
на ψ
∗
µ
,а Aψ
µ
∗
µψ
∗
µ
на ψ
λ
, и проинтегри-
ровав, получим
λ
Z
dx ψ
∗
µ
ψ
λ
µ
Z
dx ψ
∗
µ
ψ
λ
,
то ес т ь
Z
dx ψ
∗
µ
ψ
λ
µ 6 λ.
В случае вырождения можно выбрать собственные функции орто-
гональными и, соответственно, использовать ортонормированную
систему функций
Z
dx ψ
∗
m
ψ
n
δ
mn
.
Полнота системы собственных функций эрмитового оператора:
f
x
X
n
a
n
ψ
n
xa
n
Z
dx
0
ψ
∗
n
x
0
f x
0
,
f
x
Z
dx
0
f x
0
X
n
ψ
n
x ψ
∗
n
x
0
.
Отсюда
X
n
ψ
n
x ψ
∗
n
x
0
δ x −x
0
.
17
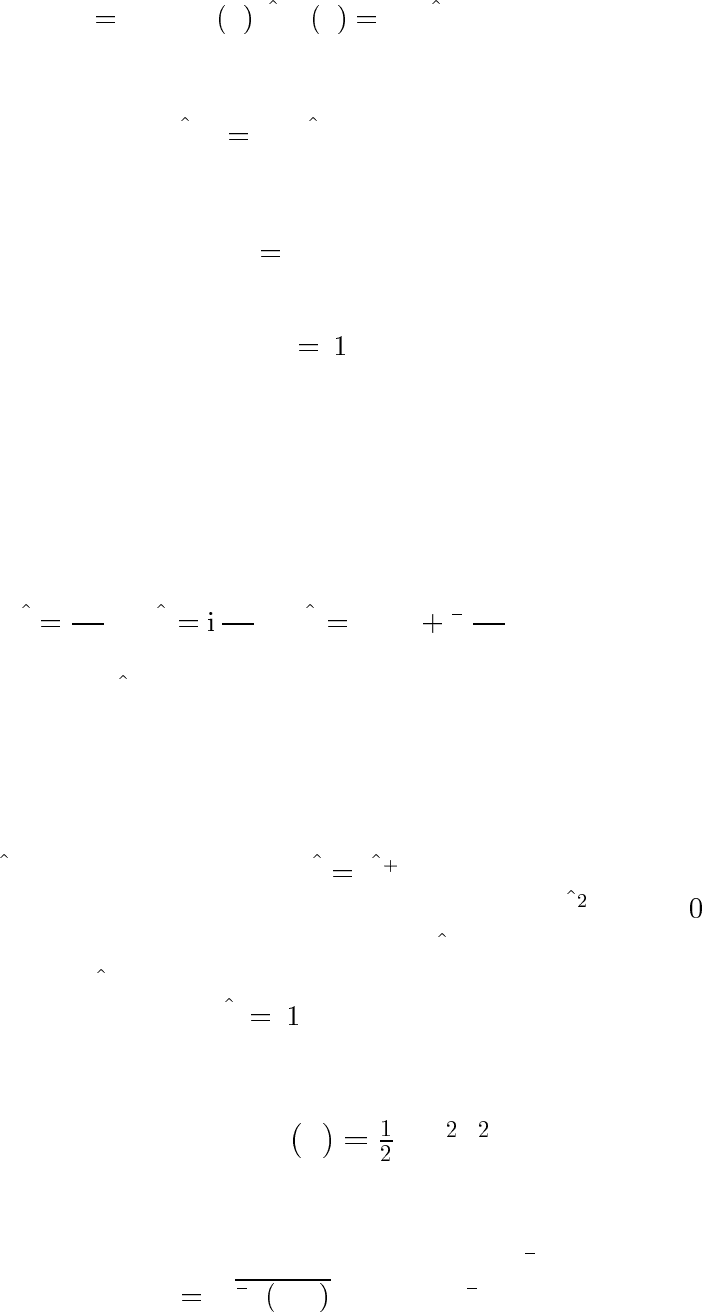
Дираковские обозначения. Матричный элемент
A
fi
Z
dx ψ
∗
f
x Aψ
i
x hf|A|ii.
В этих обозначениях эрмитовость имеет вид
hf|
A|ii
hi|A|fi
∗
,
ортонормируемость означает
hf|ii
δ
fi
,
аполнота—
X
n
|nihn| .
ВОПРОСЫ
6.1. Найти операторы, сопряженные к операторам
A
d
dx
,
B
d
dx
,
C mωx h
d
dx
.
6.2. Для оператора
C, определенного в предыдущей задаче, най-
ти собственные функции и собственные значения. Проверить, что
собственные значения этого оператора могут быть комплексными,
а собственные функции, отвечающие различным собственным зна-
чениям, не обязательно ортогональны.
6.3. Пусть
A — эрмитов оператор, A A . Покажите, что среднее
значение квадрата этого оператора неотрицательно hψ|
A |ψ i≥ .
6.4. Найти собственные функции оператора
x в x-иp-представлениях.
То же для оператора
p.
6.5. Найти вид оператора
A /r в импульсном пространстве
(задача 1.47 ГКК).
§7. Линейный осциллятор U x mω x
Уровни энергии и волновые функции
В этой задаче естественная система единиц включает
h, m, ω. Из них
строится единица длины `
q
h/ mω , энергии hω и т.д. (найдите
18
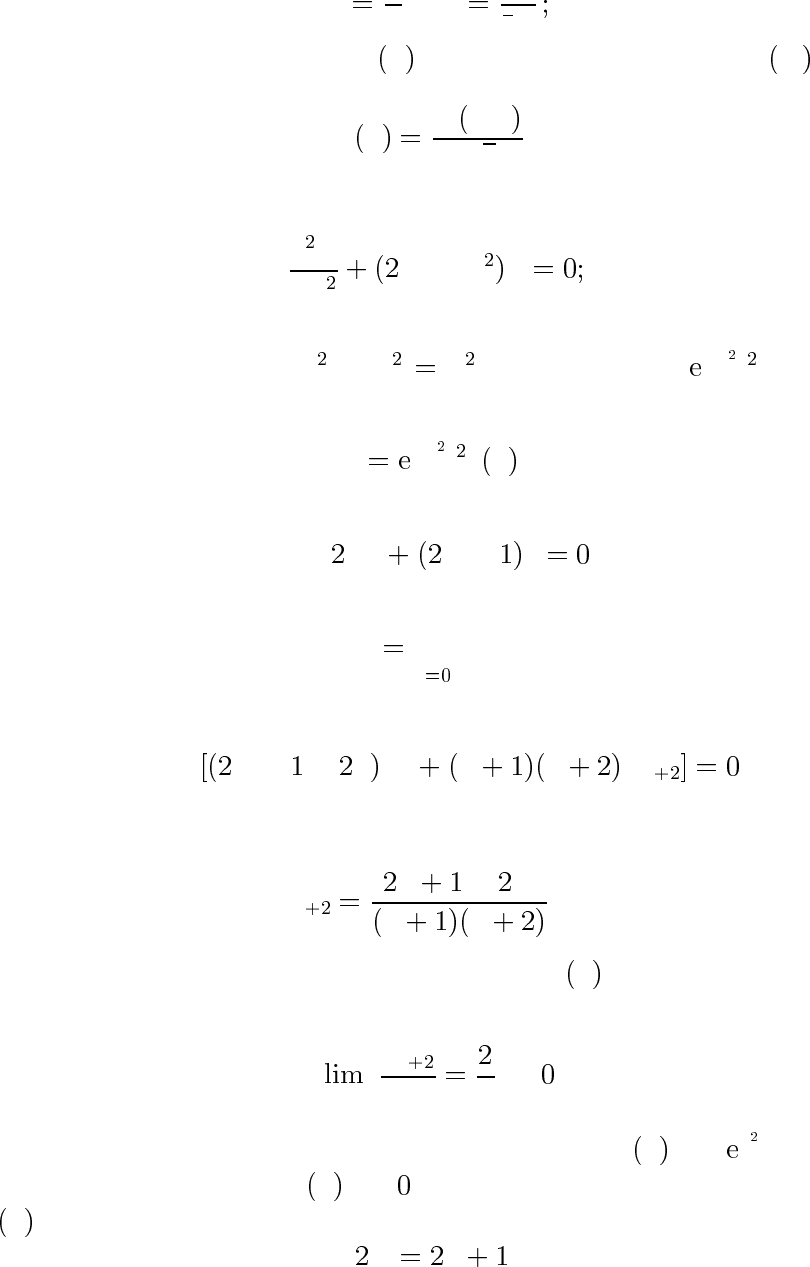
единицы времени, скорости, импульса, силы). Перейдем к безраз-
мерным величинам
x
0
x
`
,E
0
E
hω
при этом волновая функция ψ x связана с безразмерной ψ
0
x
0
соот-
ношением
ψ
x
ψ
0
x/`
√
`
.
Тогда мы получим УШ в виде
d
ψ
dx
0
E
0
−x
0
ψ
в дальнейшем штрихи опускаем.
При x →±∞имеем d
ψ/dx x ψ,тоестьψ→
±x/
.Поэтому
ищем нормируемые, убывающие на бесконечности решения в виде
ψ
−x /
v x ,
где
v
00
− xv
0
E−v .
Ищем v в виде ряда
v
∞
X
n
a
n
x
n
Возникающее таким образом уравнение
X
n
x
n
E − − n a
n
nn a
n
приводит к рекуррентному соотношению для коэффициентов
a
n
n −E
nn
a
n
.
Оно означает, в частности, что функция v
x содержит слагаемые
одинаковой четности. Условие
n→∞
a
n
a
n
n
→
обеспечивает сходимость ряда при всех x,ноvx →
x
при x →
±∞ . Чтобы получить ψ
x → при x →±∞, необходимо ряд для
v
x оборвать, положив
E n .
19
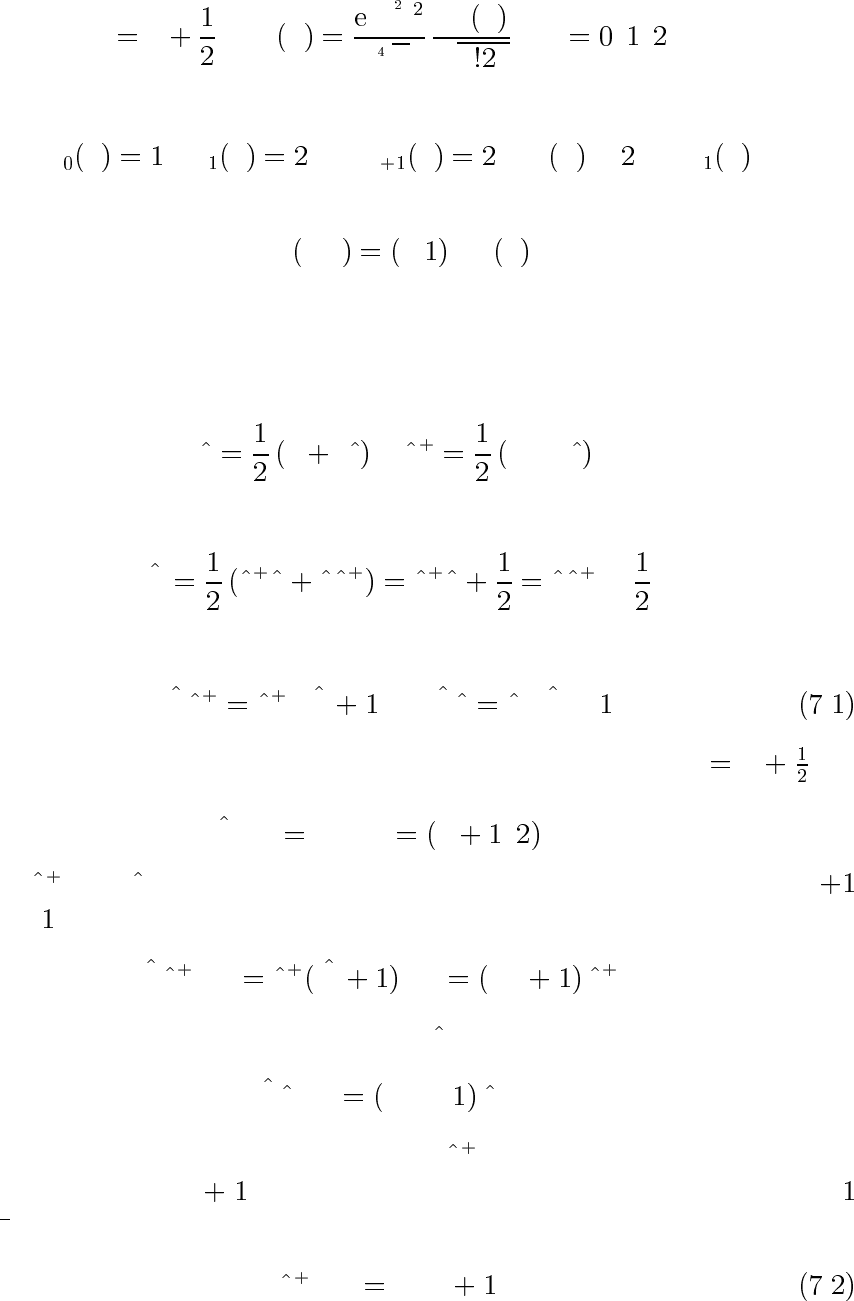
В итоге получаем уровни энергии и нормированные волновые функ-
ции
E
n
n ,ψ
n
x
−x/
√
π
H
n
x
√
n
n
,n ,,,... .
Здесь H
n
– полиномы Эрмита:
H
x ,H x x, H
n
x xH
n
x − nH
n−
x .
Отметим, что
ψ
n
−x −
n
ψ
n
x .
Операторы рождения и уничтожения
Введем операторы
a x ip , a x −ip ,
через которые гамильтониан записывается в виде
H aa aaaaaa−.
Нетрудно показать, что
Ha a
H
,Haa
H−
..
Пусть |ni — нормированное состояние с энергией E
n
n ,то
ест ь
H |ni E
n
|ni n /|ni.
Тогд а
a |niи a |ni— состояния (ненормированные) с энергией E
n
иE
n
−соответственно. Действительно, из (7.1) следует, что
Ha |ni a H |niE
n
a|ni,
а также аналогичное уравнение для
a|ni:
Ha|ni E
n
− a |ni.
Таким образом, действие оператора
a на состояние |ni переводит
его в состояние |n
i, то есть повышает энергию состояния на
(на hω в обычных единицах),
a |n i c
n
|n i,.
20
