Сербо В.Г., Хриплович И.Б. Конспект лекций по квантовой механике

Подождите немного. Документ загружается.

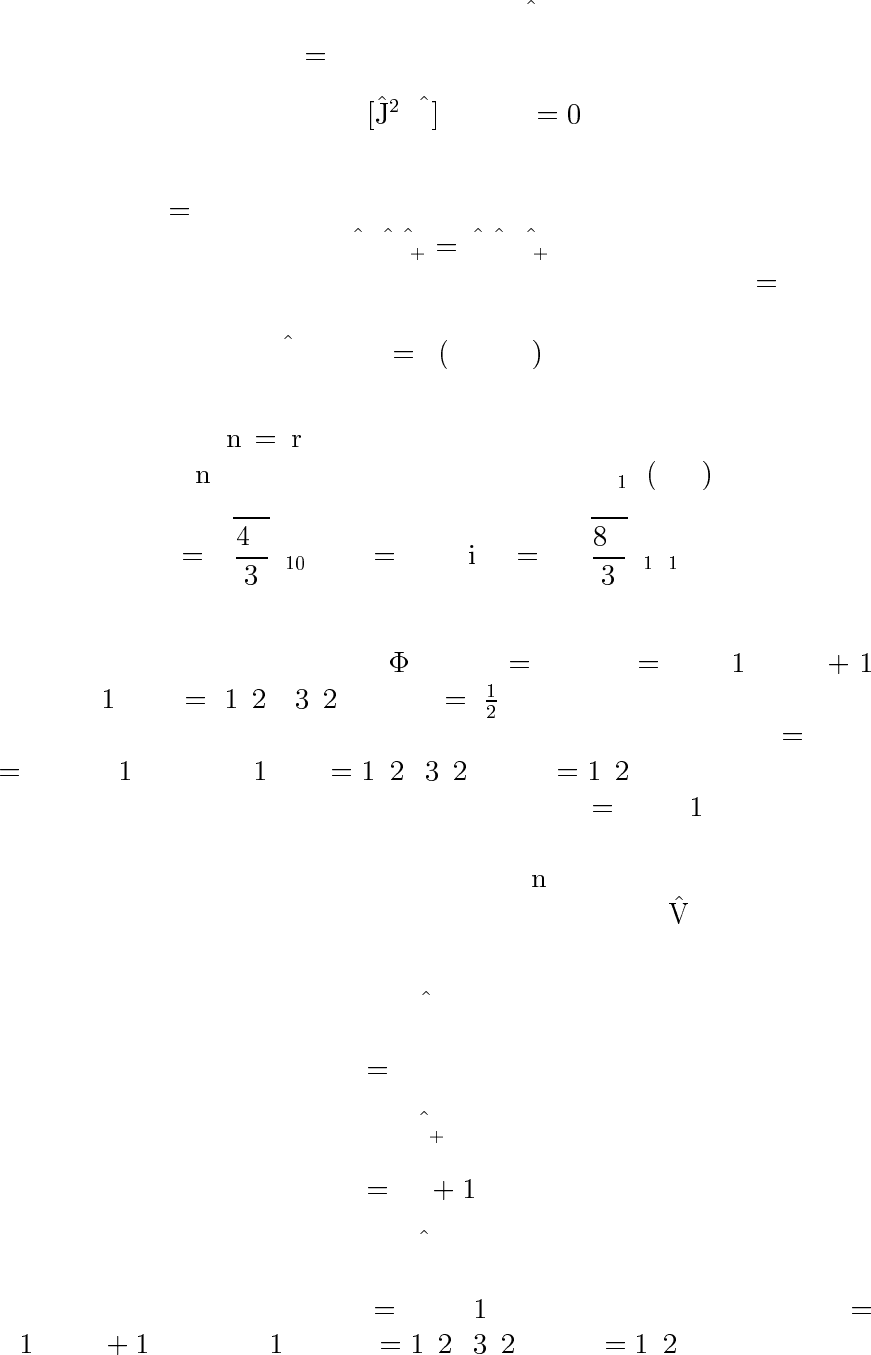
следует, что матричный элемент hJ

|S |JMαiможет быть отли-

чен от нуля лишь при M

M. Аналогично, из соотношения

| ,S |JMαi

следует, что этот же матричный элемент может быть отличен от ну-

ля лишь при J

J. Наконец, рассматривая матричные элементы от

операторных равенств типа

−

SJ SJ

−

J , получим, что обсужда-

емый матричный элемент вообще не зависит от M (при M

M), то

ест ь

|S |JMαi a J, α, α

В качес тве п ро сто г о п р им ер а векторного оператора рассмотрим

единичный вектор

/r. Известны соотношения между компо-

нентами вектора

и сферическими функциями Y

θ, ϕ :

Y ,n

±n

∓

Отсюда ясно, что произведение n

|JMαi может быть представлено

в виде суперпозиции функций

с m M и j J − , J, J

при J ≥ и j / , / при J . Поэтому матричный эле-

мент hJ

|JMαi может быть отличен от нуля при M

M и

J, J ± при J ≥ и J

/ , / при J / . Аналогично, для

|JMαi получим правила отбора M

M ± итежепра-

вила отбора для J. Существенным для доказательства этих правил

отбора был не конкретный вид оператора

, а его векторный харак-

тер. Поэтому и для любого векторного оператора

справедливы

правила отбора: матричный элемент

|JMαi

отличенотнулялишьприM

M, матричный элемент

|V |JMαi

отличенотнулялишьприM

M , а матричный элемент

−

|JMαi

отличен от нуля лишь при M

M − , и во всех этих случаях J

J − , J, J при J ≥ или J

/ , / при J / .

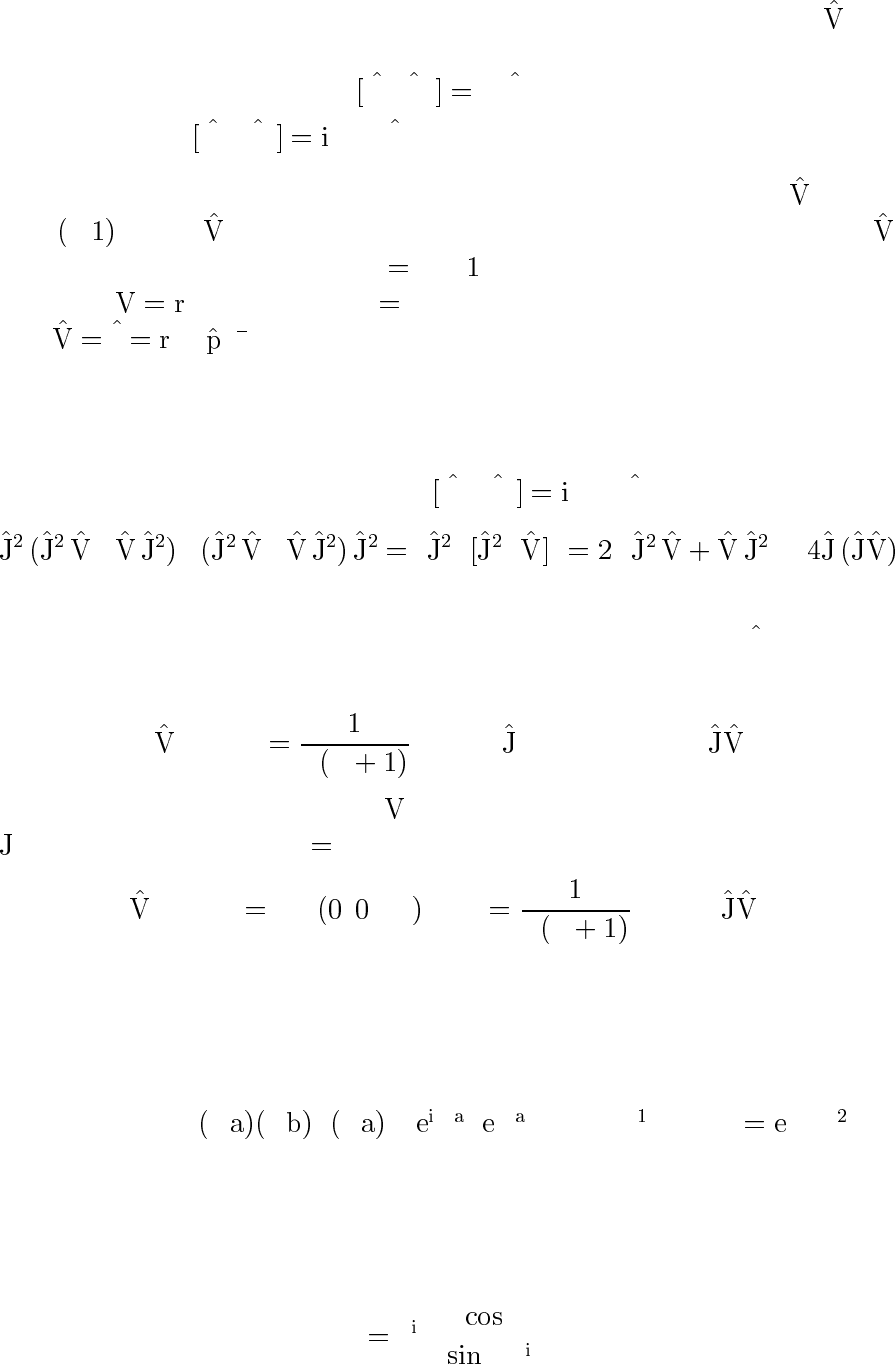
Найдите правила отбора по M для векторного оператора ,ис-

пользуя соотношение

±V

следующее из

mnl

Дополнительные правила отбора. Четность состояния

рав-

на ∓

−

,если — полярный (аксиальный) вектор, поэтому hl

| |lmi

отличенотнулялишьприl

l± для полярного вектора (напри-

мер, для

)илишьприl

lдля аксиального вектора (например,

для

l × /h).

§28. Усреднение векторного оператора

Используя правила коммутации J

mnl

, покажите, что

− − −



, ,

  

−.

Взяв от этого соотношения матричный элемент по состояниям |JM

αi

и |JMαi, отличающимся лишь значениями проекции

,получим

формулу усреднения

hJM

α| |JMαi

J J

hJM

α| |JMαi·hJMα| |JMαi,

то есть усредненный вектор

направлен по усредненному вектору

. В частности, при M

M получаем

hJMα|

|JMαi C · , ,M ,C

hJMα| |JMαi.

ВОПРОСЫ

28.1. Найти

σ σ ; σ

;

; Uσ

−

,гдеU

iσ

ϕ/

28.2. Задача 5.4 ГКК. Могут ли квадраты проекций электронного

спина на оси x, y, z иметь одновременно определенные значения?

28.3. Задача 5.12 ГКК. Показать, что для состояния, описываемо-

го спиновой волновой функцией





αe





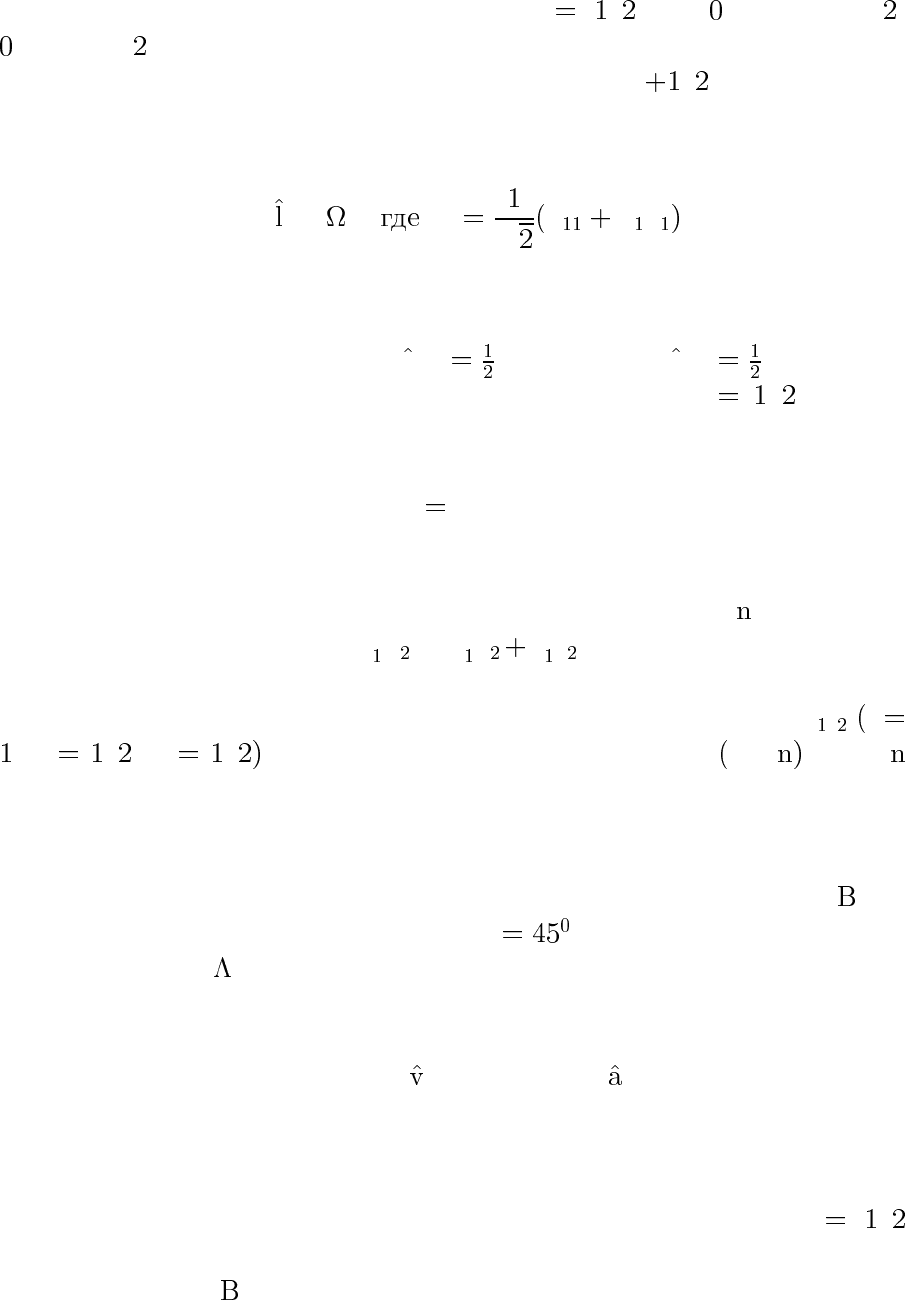
(это наиболее общий вид нормированной волновой функции спи-

нового состояния частицы со спином s

/ при ≤ α ≤ π/ ,

≤ β< π), можно указать такую ось в пространстве, проекция

спина на которую имеет определенное значение

/ .Найтиполяр-

ный и азимутальный углы этой оси.

28.4. Найти

∗

ψd , ψ

√

Y Y

−

и сравнить полученный результат с результатом предыдущей зада-

чи.

28.5. Найти χ, для которой

χ χ.Тожедляs

χ χ.

28.6. Задача 5.15 ГКК. Для частицы со спином s

/ указать

закон преобразования спиновой волновой функции









при вращении системы координат на угол ϕ относительно оси, на-

правление которой определяется единичным вектором

Показать, что величина χ

∗

χ ≡ a

∗

a b

∗

b не меняется при указан-

ном преобразовании, то есть является скаляром.

28.7. Показать, что угловая волновая функция состояния p

,s /,j / может быть представлена в виде −σ χ,где

— орт радиус-вектора, χ — обычный двухкомпонентный спинор.

28.8. Найти относительные интенсивности расщепленных пуч-

ков нейтронов в опыте типа Штерна–Герлаха, если поляризованные

вд оль ос и x нейтроны движутся вдоль оси z, а магнитное поле

на-

правлено в плоскости xy под углом α

косиx.

28.9. Распад

→ pπ

−

(Фейнмановские лекции по физике. Вып.

9, гл. 15, § 5).

28.9. Спин в магнитном поле (задачи 7.40-7.42 и 7.44 ГКК).

Найти операторы скорости

и ускорения (в шредингеровском

представлении) нейтральной частицы (например, нейтрона), нахо-

дящейся в магнитном поле.

Найти зависимость от времени спиновой функции и средних зна-

чений компонент спина нейтральной частицы со спином s

и магнитным моментом µ, находящейся в однородном постоянном

магнитном поле

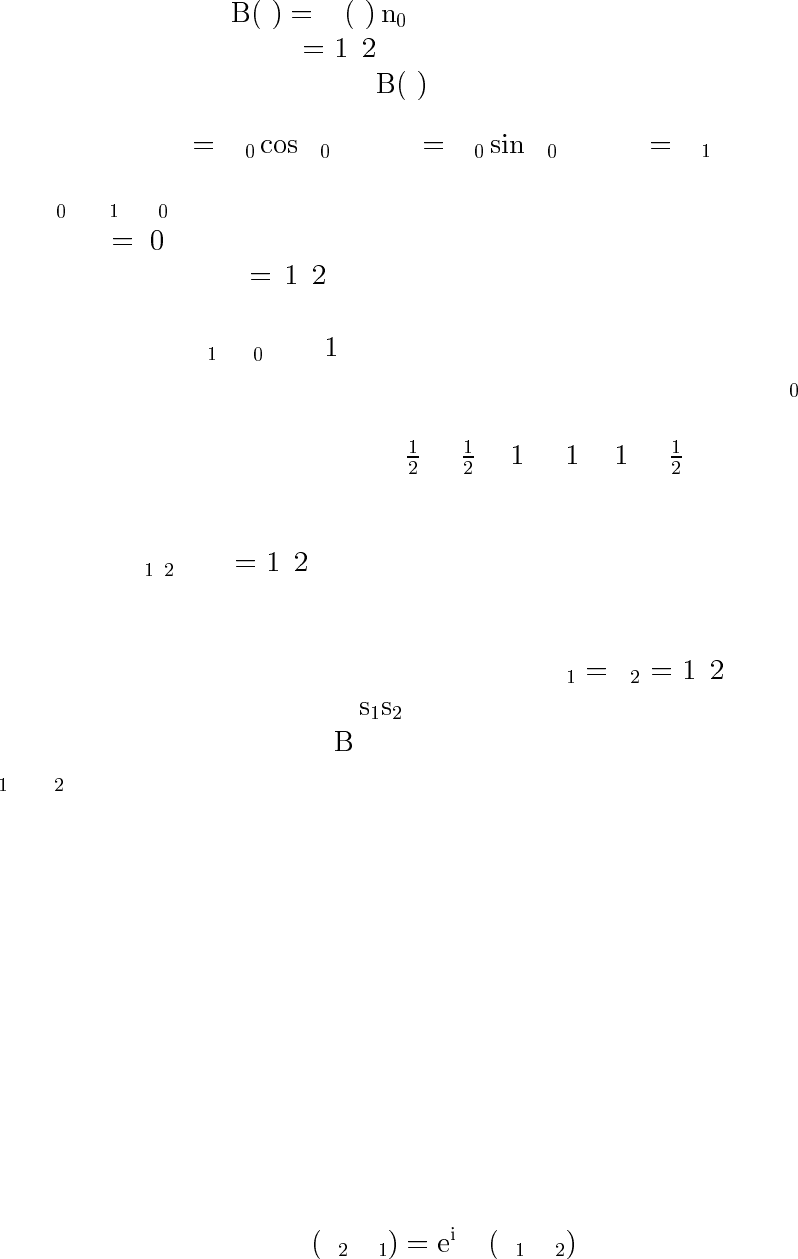
Обобщить результат предыдущей задачи на случай однородно-

го непостоянного магнитного поля, направление которого остается

неизменным, т. е.

t Bt.

Частица со спином s

/ и магнитным моментом µ находится в

однородном магнитном поле

t вида

B ω t, B

B ,

где B

,B,ω – постоянные величины.

При t

частица находилась в состоянии с проекцией спина

на ось z,равнойs

/ . Найти вероятность различных значений

прекции спина на ось z вмоментвремениt. Обсудить, в частности,

случай, когда |B

/B | ; обратить внимание на резонансный ха-

рактер зависимости вероятности “переворота” от частоты ω

в этом

случае.

28.10. Сложение моментов

× , × , × (в том числе с

использованием таблиц коэффициентов Клебша-Гордана).

28.11. Найти среднее значение магнитного момента электрона в

состоянии p

с j

/ двумя способами: а) используя результаты

предыдущей задачи; б) используя формулу усреднения векторного

оператора.

28.12. Система состоит из двух спинов s

s / ,взаимодей-

ствие которых имеет вид K

. Найти уровни энергии системы во

внешнем магнитном поле

, если гиромагнитные отношения равны

и g .

28.13. Найти правила отбора для матричных элементов диполь-

ного hl

|lmi и квадрупольного hl

|lmi моментов.

28.14. Найти в борновском приближении сечение рассеяния бы-

стрых нейтронов кулоновским полем (Задача 13.43 ГКК, а также

§ 42 из книги Берестецкого, Лифшица и Питаевского ”Квантовая

электродинамика” (М.: Наука, 1989).

§29. Тождественность частиц

Благодаря отсутствию точной локализуемости в квантовой механи-

ке тождественность частиц приводит к их неразличимости. Поэтому

x ,x

ψ x ,x .

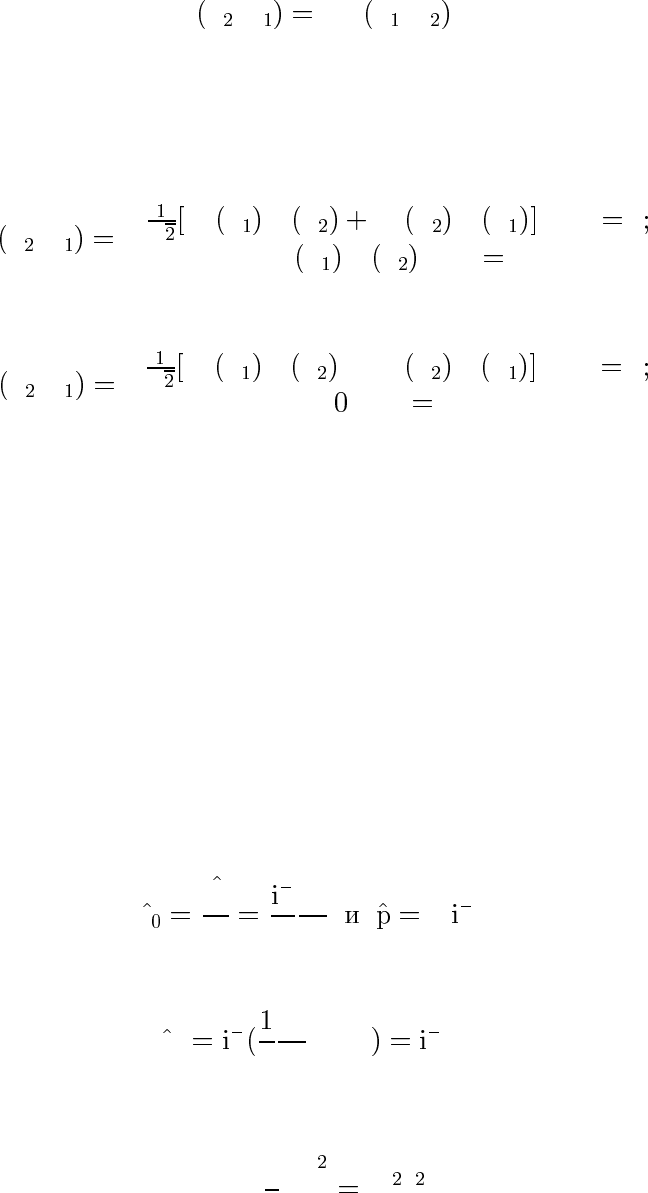
Так как двухкратная перестановка двух частиц — тождественная

операция, то

x ,x ±ψ x ,x .

Благодаря принципу суперпозиции, симметрия всех состояний фи-

зической системы одинакова.

Волновая функция бо зо нов симметрична относительно переста-

новок

x ,x







√

x ψ

xψ

x,a6b

xψ

x,a b.

Волновая функция фермионов антисимметрична:

x ,x

(

√

x ψ

x −ψ

x ψ

x ,a6b

,a b.

Принцип Паули: два фермиона не могут находиться в одном

состоянии. Он обеспечивает стабильность атома — системы элек-

тронов (частиц со спином 1/2).

В релятивистской квантовой теории поля доказывается теорема

Паули о связи спина со статистикой: частицы с целым спином —

бозоны, частицы с полуцелым спином — фермионы.

Составная частица, построенная из четного числа фермионов —

бозон, из нечетного числа фермионов — фермион.

§30. Уравнение Клейна–Фока–Гордона

Операторы

∂

∂t

−h∇

образуют 4-мерный вектор

∂

∂t

, −∇

h∂

Из классического соотношения для компонент 4-импульса реляти-

вистской частицы

p −

m c ,

где A

A ϕ, — 4-потенциал электромагнитного поля, сле-

дует релятивистское волновое уравнение (

− г.)





∂

−

− h∇−





m c . .

Четырехмерная плотность тока

(

∗

h∂

−

−h∂

∗

)

сохраняется:

∂

Уравнение (30.1) и плотность тока j

инвариантны относительно ка-

либровочного преобразования (сравни с нерелятивистским случаем

в §19)

→ A

−∂

f x , →

ef x /hc

, .

где f x — произвольная функция.

Релятивистская поправка к закону дисперсии, то есть к зависимо-

сти энергии от импульса,

m c −mc −

≈−

m c

снимает вырождение по l в спектре кулоновой задачи, приводит к

тонкой структуре уровней. Возникающая поправка к энергии рав-

на (см. уравнения (10.1) и (17.2))

hnl|V |nli −













−













−





l /

−





Здесь

≈

— безразмерная константа, постоянная тонкой структуры.











)

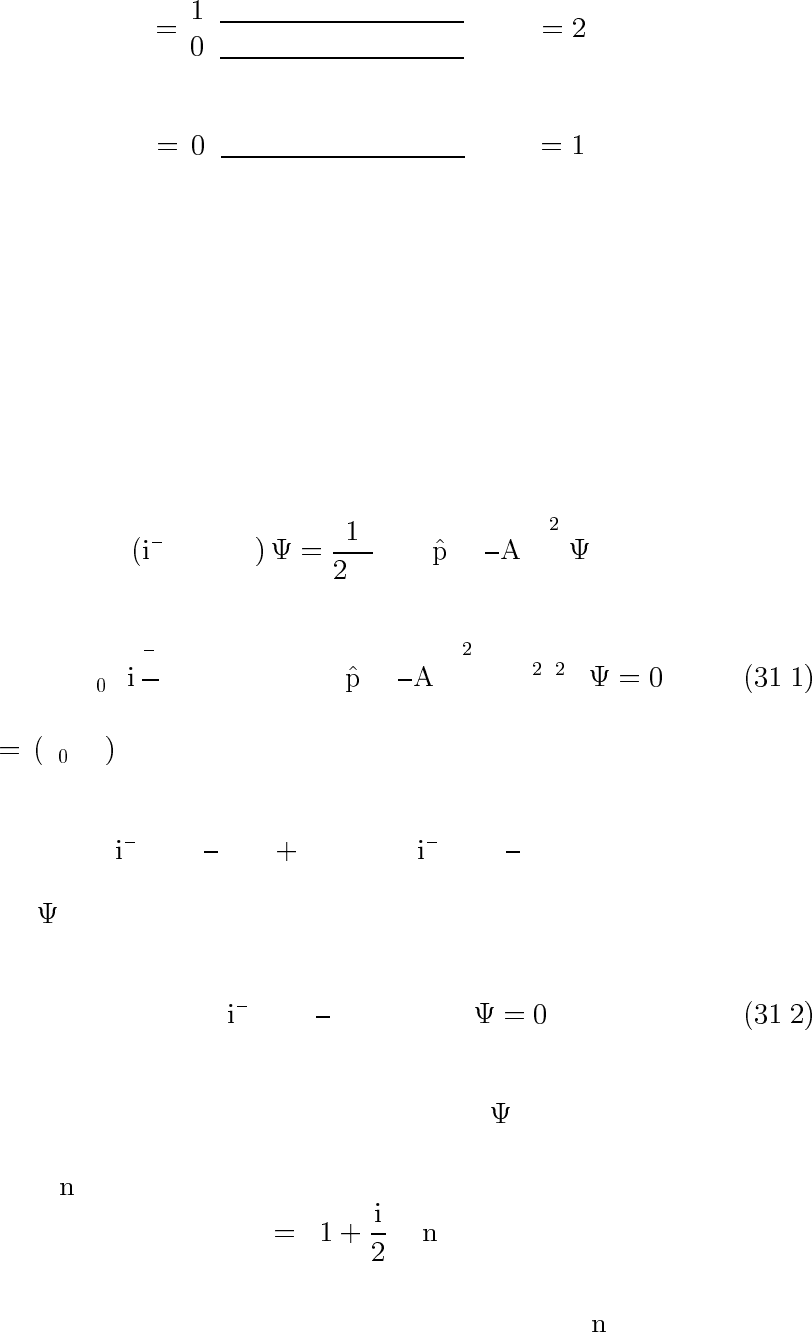
l }n

Тонкая структура уровней атома водорода согласно (30.2).

Однако реальный спектр атома водорода отличается от этого спек-

тра. Причина в том, что уравнение (30.1) не учитывает спин элек-

трона.

§31. Уравнение Дирака

Естественное релятивистское обобщение уравнения Паули (см. §25)

h∂

− eϕ

−

которое учитывает спин электрона, выглядит так:







∂

−eϕ

− γ

−

− m c







, .

где γ

γ , γ — некоторые матрицы. Оператор второго порядка

{...} в левой части уравнения (31.1) факторизуется:

h∂

−

h∂

−

− mc

Функция

удовлетворяет уравнению (31.1), если она является ре-

шением уравнения первого порядка

h∂

−

− mc

. .

Это и есть уравнение Дирака (1928 г.).

Сколько компонент у волновой функции

Бесконечно малый поворот 2-компонентного спинора на угол θ

вокруг оси

θσ

сохраняет P-инвариантность (то есть инвариантность относительно

отражений), так как и момент σ, и ось поворота

— аксиальные

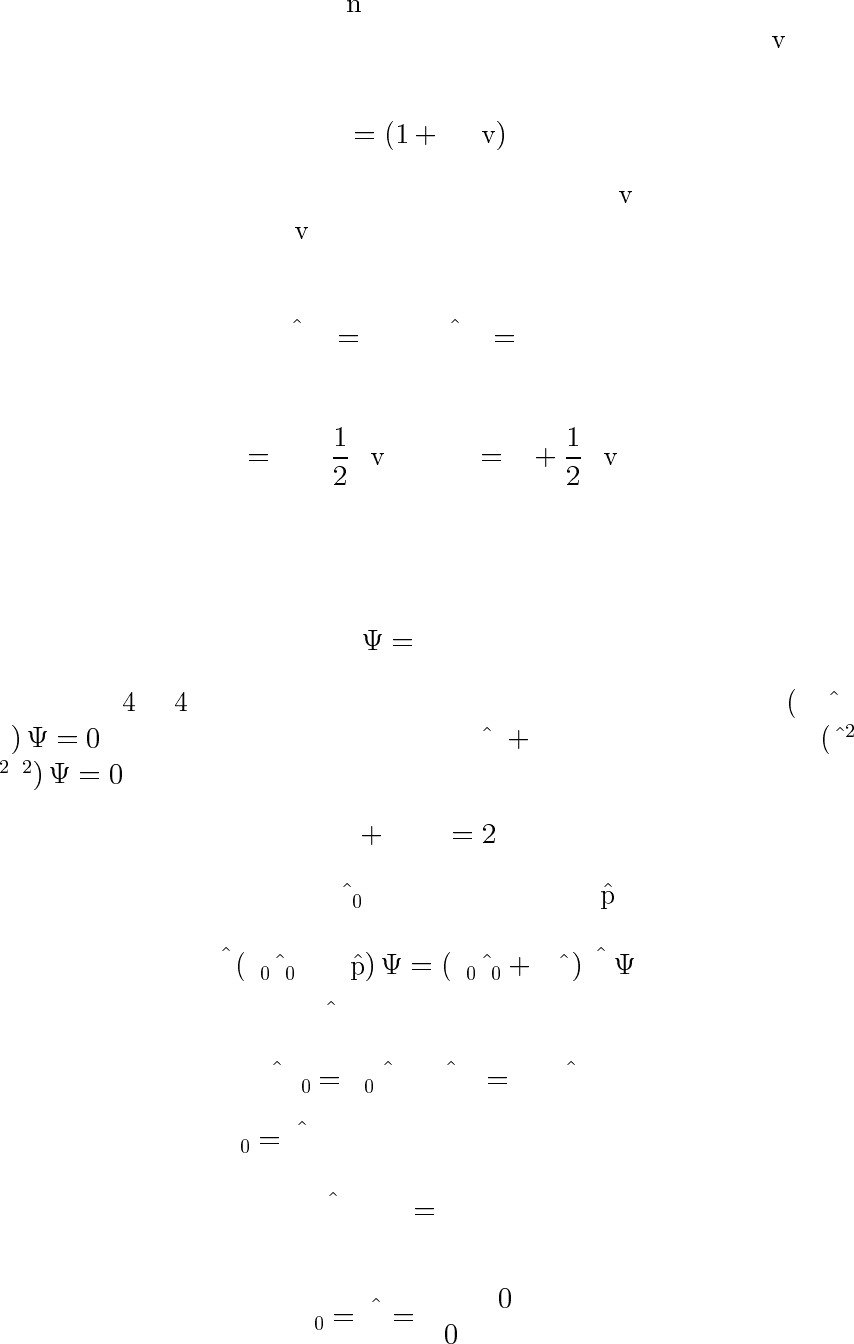
векторы; соответственно, σ — скаляр. Но единственно возможное

бесконечно малое преобразование Лоренца со скоростью

для 2-

компонентного спинора

λσϕ

нарушает P-инвариантность, так как скорость

— полярный век-

тор, а следовательно, σ

— п севд ос кал я р ( то ест ь м е ня ет з н ак п р и

отражении координат). Поэтому приходится вводить второй спинор

χ. Если

Pϕ ϕ, то Pχ −χ.

И тогда преобразование Лоренца вида

ϕ − σ χ, χ

χ σ ϕ

P -инвариантность сохраняет.

Двухкомпонентные спиноры ϕ и χ объединяются в 4-компонентный

спинор, или биспинор

Найд

ем

× матрицы γ

. Свободное уравнение Дирака γ

−

под действием оператора γ

mc должно перейти в p−

c. Отсюда следует

µν

При отражении координат

p не изменяется, а изменяет знак. По-

этом у

P γ p −γ γ p γp

P .

Та ки м об ра з ом, матрица

P удовлетворяет условиям

Pγ γ P, Pγ −γP.

Я сн о п оэтом у, ч то γ

P . С другой стороны, по определению,

−χ

так что

−I

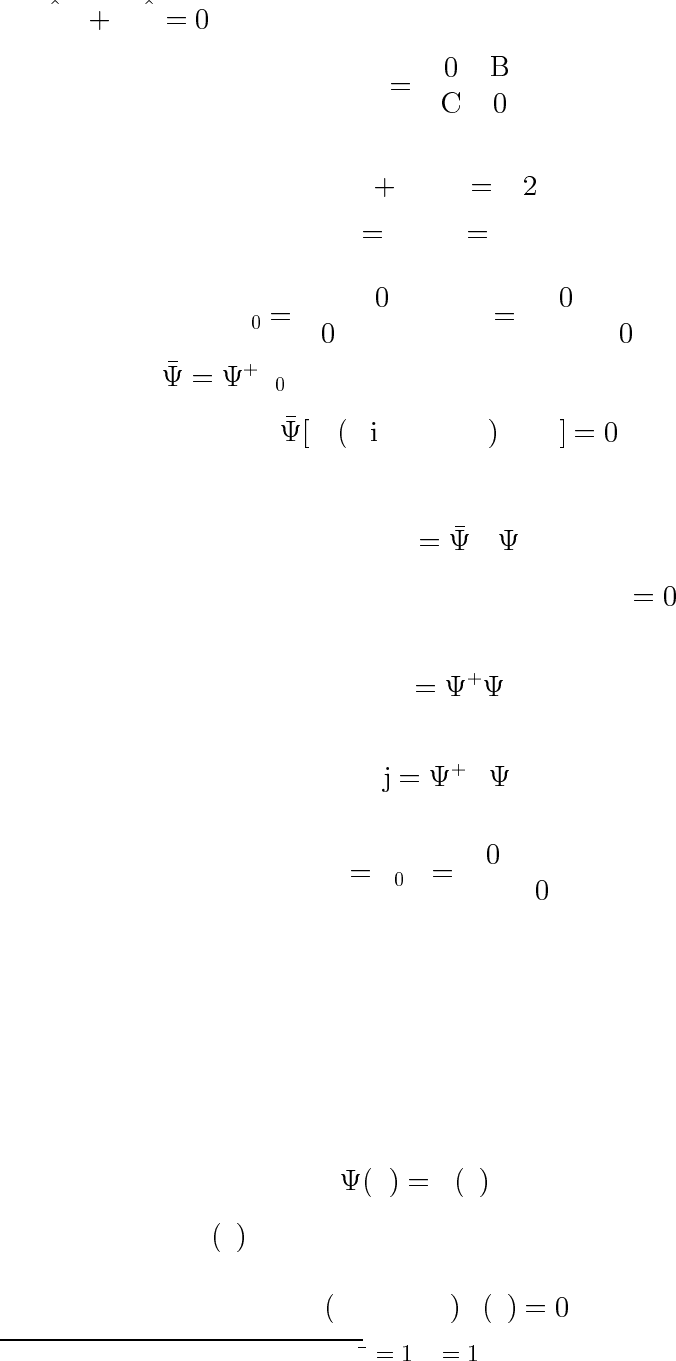
Из Pγ γP следует, что

А соотношение

− δ

удовлетворяется, если B

−C

,гдеσ

— матрицы Паули.

Итак,

−I

, γ

−σ

Функция

γ удовлетворяет уравнению

− ∂

− eA

− m ,

где производная ∂

действует налево. 4-мерная плотность тока

удовлетворяет уравнению непрерывности ∂

Для дираковской частицы плотность вероятности равна

а плотность тока —

α ,

где матрицы

γ γ

эрмитовы.

Уравнение Дирака и плотность дираковского тока, разумеется,

инвариантны относительно калибровочного преобразования (30.2).

Свободное движение дираковской частицы

Cвободному движению соответствует плоская волна

x upe

где биспинор u

p удовлетворяет системе алгебраических уравне-

ний

−m u p .

Зд есь и ниже в §32 полагаем h ,c.

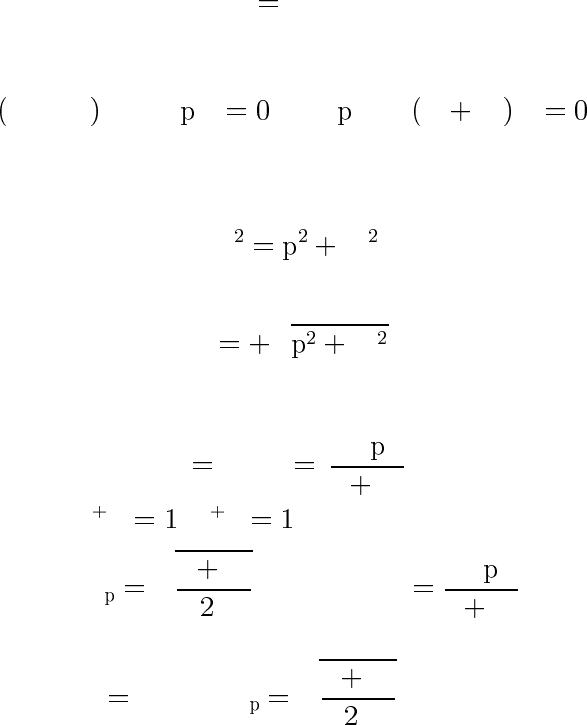
Для двухкомпонентных спиноров, через которые выражается

получаем систему уравнений

E −m ϕ −σ χ , σ ϕ − E m χ .

Эта система имеет ненулевое решение, если ее определитель равен

нулю, то есть при условии

m .

Введ

ем арифметический, положительный корень

m .

Существуют две возможности(рис. 12):

ε, χ

ε m

ϕ.

При нормировке ϕ

ϕ , u u ,

ε m

Aϕ

ε m

−ε, u

−ε,

ε m

−Aχ

Четыре компоненты волновой функции соответствуют двум воз-

можным ориентациям спина при двух возможных знаках энергии.

Исключить состояния с отрицательной энергией нельзя, так как

в ква нто вой м ехан ике возм ож ны пе реходы между со стоян ия ми . Д и-

рак постулировал, что уровни с отрицательной энергией заполнены.

Тогда переходов на них нет в силу принципа Паули. Дырка в дира-

ковском море ведет себя как частица той же массы, что и электрон,

но с противоположным зарядом, то есть является позитроном.

Рождение электрон-позитронных пар постоянным внешним элек-

трическим полем

Рождение электрон-позитронных пар внешним электрическим по-

лем — замечательное предсказание релятивистской квантовой ме-

ханики (Заутер, 1931 г.; Швингер, 1951 г.). Напряженности элек-

трического поля, достаточно большие для реального наблюдения