Щербин С.А., Семёнов И.А., Щербина Н.А. Основы гидравлики

Подождите немного. Документ загружается.

ной жидкости начинает колебаться, затем размываться и перемеши-

ваться с массой воды. Становится заметным вихреобразное, хаотичное

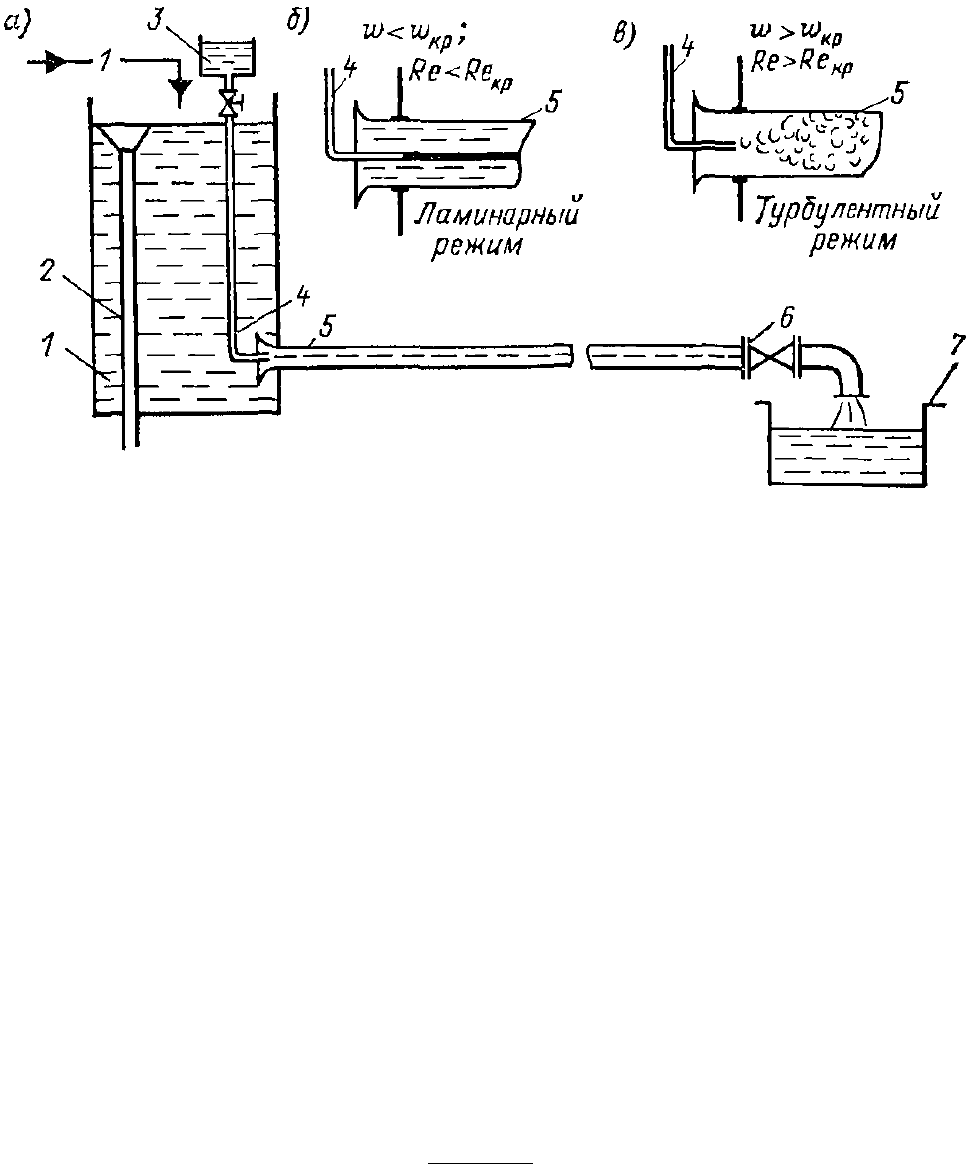
движение частичек жидкости (рис. 28, в). Такое движение жидкости,

сопровождающееся интенсивным ее перемешиванием, называется

турбулентным.

Рис. 28. Опытная установка Рейнольдса для изучения режимов движения

жидкости: а) – схема установки; б) – ламинарный режим течения жидкости; в) –

турбулентный режим течения жидкости; 1 – сосуд с водой; 2 – сливная труба; 3

– напорный бак; 4 – трубка; 5 – стеклянная труба; 6 – кран; 7 – сливной бак.

Критическая скорость

кр

W не является постоянной величиной.

Она уменьшается при увеличении диаметра трубки, и возрастает при

увеличении вязкости жидкости. Следует так же отметить, что пере-

ход от ламинарного движения жидкости к турбулентному происходит

при большей скорости, чем обратный процесс. Так же было опытно

доказано, что критическая скорость уменьшается при движении жид-

кости в

сужающихся трубах, и возрастает – при движении в расши-

ряющихся.

Исходя из опытов, Рейнольдс вывел безразмерный критерий, с

помощью которого можно определить режим движения жидкости.

Этот критерий был назван критерием Рейнольдса:

⋅

Re , или

(50)

⋅

=Re ,

где

– скорость движения жидкости, м/с; d – диаметр трубы, м;

– плотность жидкости, кг/м

;

– коэффициент динамической вяз-

кости жидкости, Па·с;

– коэффициент кинематической вязко-

сти жидкости, м

/с.

Критической скорости

кр

W соответствует критическое значение

критерия Рейнольдса

кр

Re . Так как критическая скорость зависит от

направления смены режима (турбулентный на ламинарный или на-

оборот), различают верхнее и нижнее критические значения

кр

Re .

Было вычислено, что они зависят от условий проведения эксперимен-

та: шероховатости стенки трубы, гладкости краев трубы на входе, на-

личия вибрации и т.д. Но в большинстве случаев используют общее

критическое значение

2300Re

≈

кр

При переходе от одного режим к другому нет четкого разграни-

чения. Поэтому на практике кроме турбулентного и ламинарного ре-

жимов используют понятие переходного режима. При

< 2300 на

характер движения потока существенное влияние оказывает вязкость

жидкости, сглаживающая мелкие пульсации скорости, и режим счи-

тается ламинарным. Если

> 2300, то большее влияние на поток

оказывают силы инерции и режим считается турбулентным (переход-

ным). При 10000Re ≥ режим называют развитым турбулентным.

В трубопроводах систем водоснабжения, вентиляции, отопле-

ния, холодильных и других машин движение, как правило, турбу-

лентное, так как движущиеся среды имеют малую вязкость и боль-

шую скорость. Ламинарный режим характерен

для жидкостей с

большой вязкостью (машинного масла, глицерина и т. п.). При не-

больших скоростях движения и малых диаметрах труб ламинарный

режим может иметь место и у маловязких жидкостей.

Критерий

Re выводился для случаев движения жидкости по тру-

бе круглого сечения. Если сечение трубопровода не круглое, вместо

диаметра в выражение (51) подставляют эквивалентный диаметр

d ,

определяемый по уравнению (36).

3.3.2 Ламинарный режим движения жидкости. Закон Стокса

Опытным путем было установлено, что при ламинарном движе-

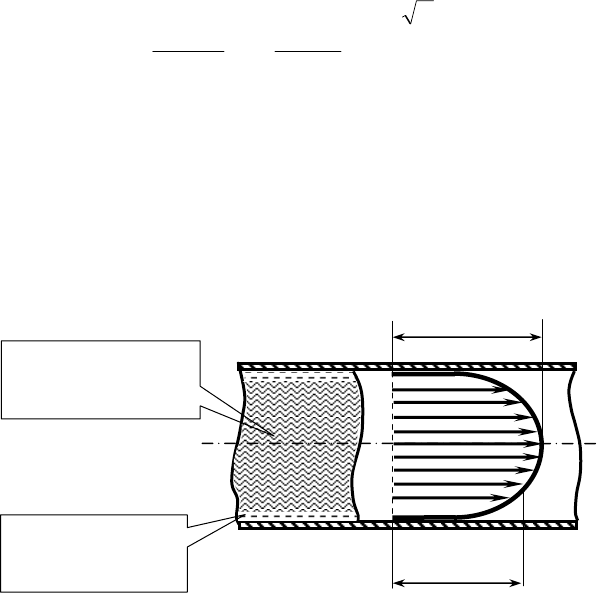
нии реальной жидкости распределение скоростей по сечению имеет

параболический характер (рис. 29). Непосредственно у стенок, в ре-

зультате значительных сил трения, скорость практически равна нулю.

По мере отдаления от стенки скорость увеличивается и достигает

максимального значения в центре потока. Неравномерность скоро-

стей в потоке является следствием наличия сил трения не только с

внутренней стенкой трубы, но и сил трения между слоями жидкости.

Рис. 29. Распределение скоростей жидкости при ламинарном движении.

Теоретический закон распределения скоростей ламинарного по-

тока по живому сечению трубопровода выражается формулой Стокса

)(

W −

⋅

(51)

где

– скорость движения слоя жидкости толщиной dy на расстоянии

y от оси трубы, м/с; i – гидравлический уклон;

– радиус трубы, м.

Исходя из закона Стокса, максимальная скорость движения

жидкости находится в середине потока. Так как расстояние y в се-

редине потока равно нулю, то максимальную скорость можно опре-

делить по выражению

max

rig

⋅⋅⋅

, или

max

dig

⋅⋅⋅

(52)

Средняя скорость жидкости при ламинарном течении равна по-

ловине максимальной скорости:

max

rig

ср

⋅⋅⋅

(53)

Тогда расход жидкости при ламинарном режиме движения

ρπ

rig

SWQ

ср

⋅⋅⋅⋅

=⋅⋅

⋅⋅⋅

=⋅=

(54)

max

3.3.3 Турбулентный режим движения жидкости

При турбулентном движении жидкости распределение скоро-

стей по сечению потока более сложное, чем при ламинарном режиме

(рис. 30). В центральной части сечения значения скоростей близки к

максимальному и слабо уменьшаются при отдалении от центра. Но в

слоях, близких к внутренней поверхности трубопровода, величины

скоростей начинают резко снижаться, стремясь к нулевому значению.

Это объясняется тем, что при турбулентном движении происхо-

дит перемешивание слоев жидкости друг с другом. Слои с макси-

мальной скоростью сталкиваются со слоями с меньшими скоростями.

В результате перемешивания скорости слоев выравниваются. У твер-

дой стенки турбулентное перемешивание затруднено, поэтому на-

блюдается резкое снижение скоростей.

Внутренний механизм турбулентного движения жидкости до

сих

пор не изучен по причине большой сложности процесса, поэтому тео-

ретических решений распределения скоростей по сечению потока нет.

Приближенно распределение скоростей при турбулентном режиме

может быть выражено степенной формулой

84,0

max

⎟

⎠

⎞

⎜

⎝

⎛

−

(55)

где

– скорость движения слоя жидкости толщиной dy на расстоянии

y от оси трубы, м/с;

– радиус трубы, м;

– коэффициент гидравли-

ческого трения (коэффициент Дарси), зависящий от шероховатости

стенок трубы.

Рис. 30. Распределение скоростей при турбулентном движении жидкости

и структура турбулентного потока.

max

ср

Ламинарный

слой

Турбулентное

На основании экспериментальных исследований определенно,

что турбулентный поток имеет на границе с твердой поверхностью

тонкий слой жидкости с ламинарным режимом. Этот слой называется

ламинарным. Толщина его очень мала и зависит от средней скорости

движения потока. Остальная часть потока – это турбулентное ядро.

Между ламинарным подслоем и турбулентным ядром существует пе-

реходный

слой со смешанным режимом движения жидкости (рис. 30).

3.4 Гидравлические сопротивления. Потери напора

Под термином гидравлические сопротивления понимают силы

трения, возникающие в реальной жидкости при ее движении.

На преодоление гидравлических сопротивлений поток жидкости

расходует часть энергии, которую называют гидравлическими потеря-

ми или потерями напора.

Гидравлические потери зависят от режима движения жидкости,

ее вязкости, от формы сечения русла и ее изменения, от шероховато-

сти стенок

. Общая сумма потерь напора

пот

h складывается из двух со-

ставляющих:

1) потерь напора по длине

тр

h , которые являются результатом

существования сил трения в равномерно движущемся потоке;

2) местных потерь напора

h , возникающих при изменении

скорости потока жидкости по величине или по направлению (вентиль,

диафрагма, резкий поворот трубопровода, сужение или расширение).

То есть

мтрпот

hhh

, м.

(56)

В гидравлике принят способ выражения гидравлических потерь

полного напора в единицах длины (метрах) и в единицах давления

(Паскалях)

Решение многих практических задач гидравлики сводится к на-

хождению зависимостей изменения скорости и давления по длине по-

тока. Для этого используют уравнение Бернулли (41) и уравнение не-

разрывности потока (38). Но так как в этих уравнениях три неизвест-

ных:

пот

hpW и ,

,то для их решения необходимо третье уравнение, ко-

торым является зависимость

(

)

Wfh

пот

Для выражения потерь напора в единицах давления (Па) используют формулу

потпот

hgp ⋅⋅=Δ

3.4.1 Потери напора по длине

Потери напора по длине обусловлены силами внутреннего тре-

ния, т.е. вязкостью жидкости. Они возрастают пропорционально длине

трубы, также существенно зависят от ее диаметра, от скорости потока,

а следовательно, и от режима течения жидкости.

Установлено, что при ламинарном режиме потери напора по

длине прямо пропорциональны средней скорости потока

Wah

тр

⋅

, м,

(57)

где

a – коэффициент пропорциональности.

Для турбулентного режима

тр

Wbh ⋅= , м,

(58)

где

b – коэффициент пропорциональности; n =1,75÷2,0 – показатель

степени.

В 1840 г. Ж. Пуазейль получил формулу для расчета потерь на-

пора на трение по длине для круглых труб при ламинарном движении

тр

⋅⋅

⋅

, м,

(59)

где

– коэффициент динамической вязкости жидкости, Па·с; l и d –

соответственно длина и диаметр трубы, м;

– средняя скорость по-

тока, м/с;

– плотность жидкости, кг/м

Анализируя выражение (60) можно отметить, что при ламинар-

ном режиме течения потери напора на трение по длине:

- прямо пропорциональны средней скорости в первой степени;

- зависят от свойств жидкости (

);

- не зависят от шероховатости стенок;

- прямо пропорциональны длине и обратно пропорциональны

квадрату диаметра трубы.

Формулу (60) можно преобразовать, и получить уравнение для

расчета потерь напора потока по длине для всех режимов движения в

общем виде:

тр

⋅⋅=

, м,

(60)

где

– безразмерный коэффициент гидравлического трения или ко-

В гидравлике среднюю скорость потока принято обозначать буквой W. Обо-

значение W

ср

употребляется только в случаях, когда местную скорость можно

спутать со средней.

эффициентом потерь на трение по длине (коэффициент Дарси);

–

удельная кинетическая энергия потока, м.

Для случая труб не круглой формы диаметр

d заменяется экви-

валентным диаметром

Коэффициент трения

зависит от скорости движения потока,

свойств жидкости, а так же от шероховатости поверхности труб. Для

разных режимов движения

рассчитывается по различным зависи-

мостям.

Для ламинарного режима величина

зависит только от кри-

терия Рейнольдса

Re:

(61)

Выражение (62) называется формулой Дарси-Вейсбаха. Она

справедлива и при турбулентном режиме движения. Однако коэффи-

циент

в этом режиме зависит не столько от Re, сколько от шерохо-

ватости поверхности труб. Определение значений коэффициента

режиме турбулентного движения довольно сложная задача – при тур-

булентном режиме пульсации скоростей и процессы перемешивания

частиц жидкости вызывают дополнительные расходы энергии, что

приводит к увеличению потерь на трение по сравнению с ламинар-

ным режимом. Вблизи стенок турбулентного потока располагается

ламинарный подслой (рис. 30, 31), толщина которого

непостоянна

и уменьшается с увеличением скорости движения жидкости, т.е. с

увеличением числа Рейнольдса:

30d

≈

(62)

Шероховатость поверхности стенок характеризуется величиной

и формой выступов, неровностей и зависит от материала и способа

изготовления и соединения труб. Она изменяется с течением времени

в результате отложения осадков, ржавления, эрозии и т. д.

Основной характеристикой шероховатости является абсолютная

шероховатость

Δ , представляющая собой среднюю высоту бугорков

и выступов. Практически очень сложно оценить фактическую высоту

выступов, поэтому пользуются понятием эквивалентной шероховато-

сти

экв

, под которой подразумевают такую однородную шерохова-

тость, которая дает потери на трение, равные потерям при действи-

тельной шероховатости.

Значения эквивалентной шероховатости

экв

в зависимости от ви-

да труб и состояния их внутренней поверхности приведены в табл. 14.

Таблица 14

Значения эквивалентной шероховатости

экв

в зависимости от материала и состояния поверхности труб

Труба Состояние поверхности

экв

Δ , мм

Бесшовная без покрытия

новая и гладкая

после нескольких лет эксплуатации

0,02÷0,1

0,15÷0,3

Бесшовная оцинкованная

новая и гладкая

после нескольких лет эксплуатации

0,1÷0,2

0,4÷0,7

Стальная

Сварная

новая и чистая

с незначительной коррозией

умеренно заржавевшая

старая заржавевшая

значительно заржавевшая или с

большими отложениями

0,03÷0,1

0,1÷0,2

0,3÷0,7

0,8÷1,5

2÷4

Чугунная

новая и гладкая

водопроводная после нескольких лет

эксплуатации

0,25÷1

1,4

Медная,

латунная,

свинцовая,

стеклянная

Новая и гладкая 0,0015÷0,01

Алюминиевая Новая и гладкая 0,015÷0,06

Эквивалентная шероховатость в зависимости от диаметра трубы

по-разному сказывается на величине гидравлических сопротивлений.

Поэтому в гидравлике для оценки гидравлических потерь используют

понятие относительная шероховатость

экв

(63)

и обратную величину - относительную гладкость

экв

Толщина вязкого подслоя

может быть больше или меньше

высоты выступов шероховатости

. Следовательно, одна и та же

труба при турбулентном режиме может быть гидравлически гладкой

или шероховатой.

У гладких поверхностей (рис. 31, а) выступы шероховатости

трубы

Δ имеют высоту намного меньшую, чем толщина ламинарного

подслоя

. Ламинарный слой полностью обволакивает все выступы и

жидкость скользит по нему, поэтому потери напора на трение опре-

деляются только лишь внутренним трением потока, и не зависят от

шероховатости стенок. Потери напора на трение по длине

тр

h в этой

области пропорциональны средней скорости

в степени n = 1,75 и

определяются по формуле (60).

У шероховатых поверхностей (рис. 31, в) толщина ламинарного

подслоя

меньше высоты выступов

. Следовательно, шерохова-

тость оказывает существенное влияние на потери. В этом случае вы-

ступы выходят за пределы ламинарного подслоя в турбулентное ядро

потока, являясь дополнительными источниками вихреобразования,

способствующими усилению процесса перемешивания. Обтекание

выступов носит резко выраженный отрывной характер. При этом зна-

чение

зависит только от шероховатости и не зависит от числа Рей-

нольдса. Потери напора на трение прямо пропорциональны квадрату

скорости (в формуле (59) 2

n ), поэтому такие участки называются

областью квадратичного сопротивления.

Возможен также переходный случай, при котором высота вы-

ступов

Δ соразмерна с толщиной

ламинарного подслоя (рис. 31, б).

В этом случае величины

тр

h и

зависят как от числа Рейнольдса,

так и от высоты неровностей

. Эта область носит название области

доквадратичного сопротивления. В уравнении (59) потери напора

прямо пропорциональны средней скорости потока в степени

75,1=n ÷ 0,2 .

Следует отметить, что понятия «гладкая» и «шероховатая» по-

верхность весьма условны. Между ними нет четкой границы. Так как

толщина ламинарного подслоя

зависит от скорости потока

, то с

увеличением скорости происходит переход от гладкой поверхности к

шероховатой.

Рис. 31. К рассмотрению гидравлически гладких и шероховатых труб: а –

гладкая труба; б – переходный случай; в – шероховатая труба.

Вывести уравнение расчета коэффициента трения

при турбу-

лентном режиме движения очень сложно из-за сложности его матема-

тического описания. Поэтому на практике использую эмпирические

зависимости и графики, например график

⎟

⎠

⎞

⎜

⎝

⎛

экв

f Re,

, составлен-

ный в 1948 г. Г.А. Мухиным для промышленных стальных труб с ес-

тественной шероховатостью (рис. 32), на котором хорошо видны три

вышеупомянутые зоны.

В справочной литературе по гидравлике [7] приводятся формулы

для нахождения

, учитывающие особенности движения потока, вид

материала и конфигурацию сечения трубы. В большинстве случаев

для определения

на практике используют следующие уравнения:

Ламинарный режим (Re < 2300) – формула Дарси-Вейсбаха (62)

Зона гладкого трения (2300 <

< 10/e) – формула Блазиуса

25,0

3164,0

(64)

Зона шероховатого трения (10/e < Re < 500/e) – формула Альт-

шуля

25,0

11,0

⎟

⎠

⎞

⎜

⎝

⎛

+⋅= e

(65)

Развитый турбулентный режим (

> 500/e) – формула Шиф-

ринсона

25,0

11,0 e⋅=

(66)