Щербин С.А., Семёнов И.А., Щербина Н.А. Основы гидравлики
Подождите немного. Документ загружается.

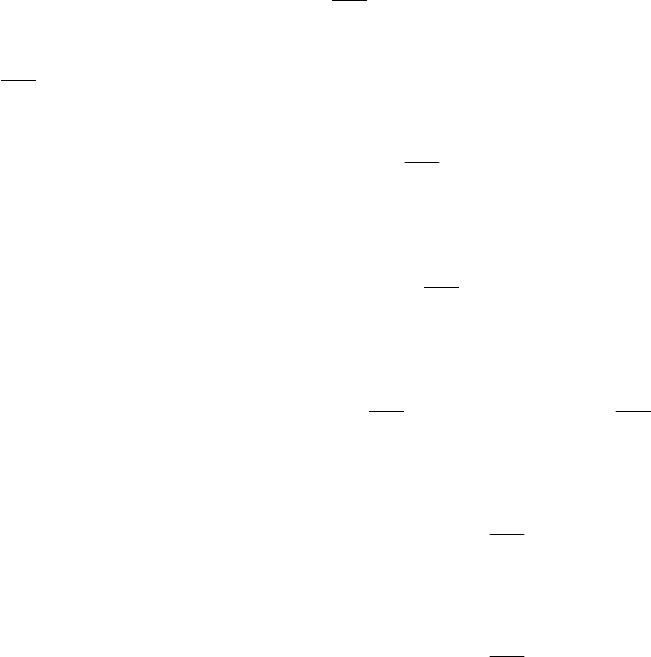
21
Сила тяжести, действующая на параллелепипед, выражается
произведением его массы dm на ускорение свободного падения g, т.е.
равна g·dm.
Сила гидростатического давления на любую из граней паралле-
лепипеда равна произведению гидростатического давления p на пло-
щадь этой грани.
Выделенный объем жидкости, находящийся под действием
внешних сил, будет находиться в равновесии, если
сумма проекций
всех действующих сил на любую из координатных осей будет равна
нулю.
Рассмотрим сумму проекций сил на ось z. Проекция силы тяже-
сти
dzdydx
g
d
V
g
dm
g
⋅
⋅
⋅
⋅
−
=
⋅
⋅
−=⋅−
ρ
ρ
.
Проекция силы гидростатического давления на нижнюю грань
dydxp
⋅
⋅
.
Если элементарное изменение гидростатического давления в на-
правлении оси z равно
z
p
∂
∂
, то по всей длине ребра
dz оно составит
dz
z
p
⋅
∂
∂
. Тогда гидростатическое давление на противоположную
(верхнюю) грань равно
⎟
⎠
⎞
⎜
⎝
⎛
⋅
∂
∂
+
dz
z
p
p и проекция силы гидростатиче-
ского давления на ось z составит
dydxdz
z
p
p ⋅⋅
⎟
⎠
⎞
⎜
⎝
⎛
⋅
∂
∂
+−
.
Проекция равнодействующей силы давления на ось z
dzdydx
z
p
dydxdz
z
p
pdydxp ⋅⋅⋅
∂
∂
−=⋅⋅
⎟
⎠
⎞
⎜
⎝
⎛
⋅
∂
∂
+−⋅⋅ .
Сумма проекций сил на ось z равна нулю, т.е.
0=⋅⋅⋅
∂
∂
−⋅⋅⋅⋅− dzdydx
z
p
dzdydxg
ρ
.
Учитывая, что
0
≠
=
⋅⋅ d
V
dzdydx , получим
0=
∂
∂
−⋅−
z
p
g
ρ
.
Проекции сил тяжести на оси x и y равны нулю. Поэтому сумма
проекций сил на ось x составит

22
0=⋅⋅⋅
∂
∂
−=⋅⋅
⎟
⎠
⎞
⎜
⎝
⎛
⋅
∂
∂
+−⋅⋅ dzdydx
x
p
dzdydx
x
p
pdzdyp
,
или
0=
∂
∂
−
x
p
.
Соответственно для оси y
0=⋅⋅⋅
∂
∂
−=⋅⋅
⎟
⎠
⎞
⎜
⎝
⎛
⋅
∂
∂
+−⋅⋅ dzdydx
у
p
dzdxdy
y
p
pdzdxp
,
или
0=
∂
∂
−
y
p
.
Таким образом, условия равновесия элементарного объема жид-
кости выражаются системой уравнений:
⎪
⎪
⎪
⎭
⎪
⎪
⎪
⎬
⎫
=
∂
∂
−⋅−
=
∂
∂
−
=
∂
∂
−
0
0
0
z
p
g
y
p
x
p
ρ
.
(10)
Уравнения (10) представляют собой дифференциальные уравне-
ния равновесия жидкости (уравнения Эйлера).
Для получения закона распределения давления во всем объеме
покоящейся жидкости необходимо проинтегрировать систему уравне-
ний (10). Интегралом этих уравнений является основное уравнение
гидростатики, широко используемое в инженерной практике.
2.3 Основное уравнение гидростатики
Для практического использования дифференциальных уравнений
Эйлера их необходимо преобразовать и проинтегрировать.
Давление в покоящейся жидкости изменяется только по верти-
кали (вдоль оси z) и остается одинаковым во всех точках любой гори-
зонтальной плоскости. Поэтому в системе уравнений (10)
0=
∂
∂
x
p
и
0=
∂
∂
y
p
, а частная производная
0=
∂
∂
z
p
может быть заменена на
0=
dz
dp
.
Соответственно можно записать
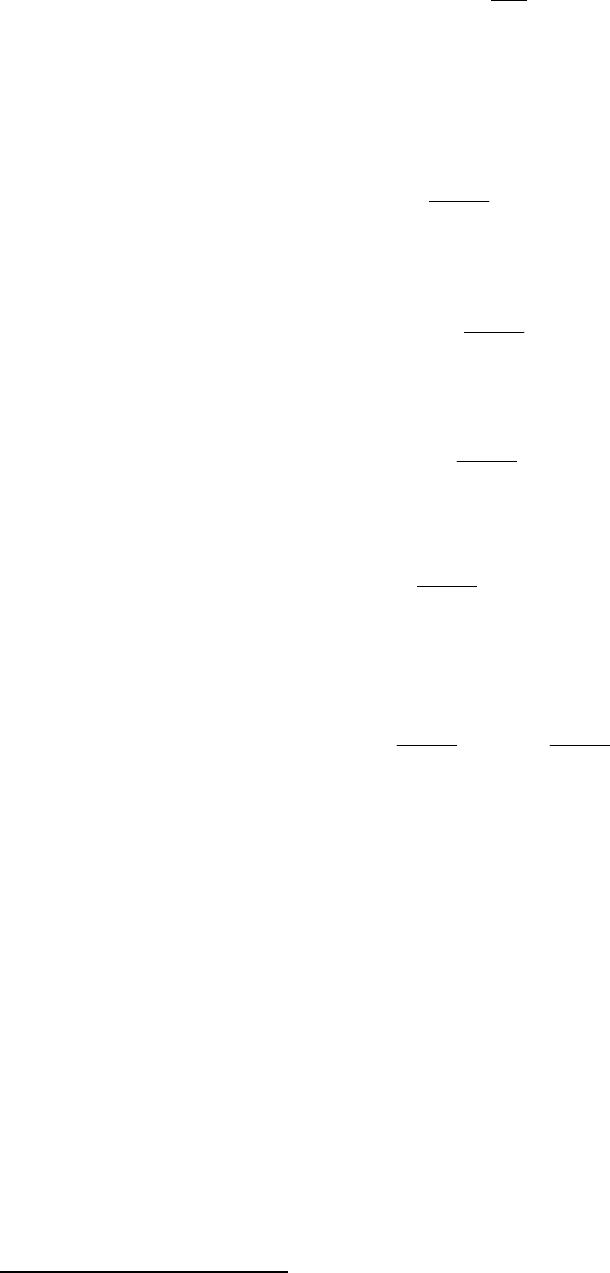
23
0=−⋅−
dz
dp
g
ρ
,
0
=
−
⋅
⋅
− dpdz
g
ρ
.
Разделив левую и правую части последнего выражения на
()
g⋅−
ρ
, получим
0
1
=⋅
⋅
+ dp
g
dz
ρ
.
Учитывая, что
cons
t
=
ρ
, запишем
0=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅
+
g
p
ddz
ρ
,
или
0=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅
+
g
p
zd
ρ
.
Окончательно после интегрирования получим
const
g
p
z =
⋅
+
ρ
.
(11)
Для двух произвольных горизонтальных плоскостей 1 и 2 урав-
нение (11) выражают в форме
g
p
z
g
p
z
⋅
+=
⋅
+
ρρ
2
2
1
1
.
(12)
Уравнение (11) или (12) называется основным уравнением гид-
ростатики. В нем
1
z и
2
z – высоты расположения двух точек внутри
покоящейся капельной жидкости над произвольно выбранной плоско-
стью сравнения
*
(отсчета), м;
1
p и
2
p – гидростатические давления в
этих точках, Па.
*
Плоскостью сравнения называют горизонтальную плоскость, проведенную на
произвольной высоте и используемую для определения вертикальных коорди-
нат отдельных точек в жидкости.
24
2.4 Закон Паскаля
Чтобы найти значение кон-
станты в уравнении (11), рассмот-
рим две частицы жидкости (рис. 6),
одна из которых (точка 1) располо-
жена внутри объема жидкости на
высоте z от плоскости сравнения 0-
0, а другая (точка 2) находится на
поверхности жидкости, т.е. на высо-
те z
0
от плоскости 0-0. Пусть p и p
0
–
давления в точках 1 и 2 соответст-
венно. При таких обозначениях
g
p
z
g
p
z
⋅
+=
⋅
+
ρρ
0
0
,
или
zz
g
pp
−=
⋅
−
0
0
ρ
;
(13)
(
)
zzgpp
−
⋅
⋅
+
=
00
ρ
.
(14)
Очевидно, что разность
(
)
zz
−
0
представляет собой глубину h
погружения точки 1 относительно поверхности жидкости (точки 2),
поэтому
hgpp
⋅
⋅
+
=
ρ
0
.
(15)
Это - другая, удобная для расчетов форма основного уравнения
гидростатики. Анализируя уравнение (15) и учитывая, что
γ
ρ
=
⋅
g
,
можно сделать вывод: давление в жидкости растет прямо пропор-
ционально глубине, и коэффициентом пропорциональности является
удельный вес жидкости.
Уравнения (14) и (15) являются математической формулировкой
закона Паскаля, согласно которому давление, производимое на по-
коящуюся капельную жидкость, передается одинаково всем точкам
ее объема. Действительно, в соответствии с уравнением (14), при из-
менении давления
0
p в точке
0
z давление
p
в любой другой точке
объема жидкости изменится так же.
1
2
p
0
p
0
0
z
0
h
z
Рис. 6. К основному
уравнению гидростатики.
25
2.5 Геометрическая интерпретация основного уравнения
гидростатики
Геометрически основное уравнение гидростатики (11) для про-
извольной точки М можно представить (рис. 7) в виде суммы двух
отрезков, высота которых равна соответственно
z и
g
p
⋅
ρ
. Величина
z называется геометрической высотой
*
, она отсчитывается от произ-
вольной плоскости сравнения
0
0
−
. Величина
g
p
⋅
ρ
определяется дав-
лением
p
в рассматриваемой точке (М) и может быть измерена так
называемой приведенной высотой
пр
h подъема жидкости в присоеди-
ненной трубке, из которой полностью удален воздух:
g
p
h
пр
⋅
=
ρ
.
Рис. 7. Геометрическая и энергетическая интерпретация основного урав-
нения гидростатики.
*
Геометрической высотой называют расстояние от плоскости сравнения до
рассматриваемой точки.

26
Сумма геометрической высоты точки z и приведенной высоты
пр
h называется гидростатическим (потенциальным) напором и обо-
значается
H
:
g
p
zhzH
пр
⋅
+=+=
ρ
.
Из основного уравнения гидростатики (11) можно сделать вывод,
что гидростатический напор для всех точек покоящейся жидкости –
величина постоянная:
const
g
p
zH =
⋅
+=
ρ
.
Так как напор для всех точек жидкости есть величина постоян-
ная, то жидкость в трубке будет подниматься на одну и туже высоту
относительно плоскости сравнения. Горизонтальная плоскость
//
00
−
,
которая располагается на высоте
(
)
пр
hzH
+
=
от плоскости сравнения
0
0−
, называется плоскостью гидростатического напора.
Если трубка открытым концом соединена с атмосферой, то такая
трубка называется пьезометром, а высота подъема жидкости в ней
п
h
(пьезометрическая высота) будет определяться избыточным (мано-
метрическим) давлением
и
p :
g
p
h
и
п
⋅
=
ρ
.
Величина, равная сумме геометрической высоты точки
z и пье-
зометрической высоты
п
h , обозначается
п
H и называется пьезомет-
рическим напором:
g
p
zhzH
и
пп
⋅
+=+=
ρ
.
Согласно основному уравнению гидростатики (11), для всех то-
чек покоящейся жидкости можно записать
const
g
p
zH
и
п
=
⋅
+=
ρ
.
Горизонтальную плоскость
////
00
−
, расположенную на высоте
()
пп
hzH +=
от плоскости сравнения
0
0
−
, называют плоскостью пье-
зометрического напора.

27
Таким образом, геометрическая интерпретация основного урав-
нения гидростатики заключается в следующем: для всех точек по-
коящейся жидкости гидростатический и пьезометрический напоры
являются величинами постоянными.
2.6 Энергетическая интерпретация основного уравнения
гидростатики
Умножим каждое слагаемое уравнения (11) на вес рассматри-
ваемого объема жидкости
g
m
⋅
:
constgm
g
p
gmz =⋅⋅
⋅
+⋅⋅
ρ
.
Произведение
g
mz ⋅⋅ представляет собой потенциальную энер-
гию массы m, находящейся в точке M на высоте z относительно плос-
кости сравнения 0-0 (рис. 7).
Преобразуем второе слагаемое:
gmhgm
g
hg
gm
g
p
пр
пр
⋅⋅=⋅⋅
⋅
⋅
⋅
=⋅⋅
⋅
ρ
ρ
ρ
.
Произведение
gmh
пр
⋅⋅ есть потенциальная энергия, необходи-
мая для поднятия массы m из точки М (рис. 7) в плоскость гидроста-
тического напора 0
/
-0
/
(на высоту
пр
h ).
Разделив оба слагаемых на
g
m
⋅
, получим удельную энергию
*
const
g
P
ze =
⋅
+=
ρ
.
Таким образом, из основного уравнения гидростатики (11) сле-
дует, что сумма удельной потенциальной энергии положения z и
удельной потенциальной энергии гидростатического давления
g
p
⋅
ρ
есть величина постоянная для всех точек покоящейся жидкости.
*
Удельной называют энергию, приходящуюся на единицу веса или массы тела.
28
2.7 Практические приложения основного уравнения гидро-
статики
Уравнение гидростатики, выражаемое часто в виде закона Паска-
ля, имеет ряд важных практических приложений.
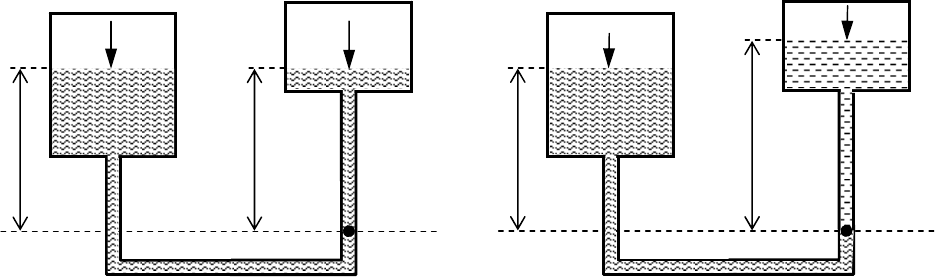
Принцип сообщающихся сосудов. Пусть два сообщающихся
сосуда (рис. 8, а) заполнены жидкостью. Выберем произвольную
плоскость сравнения 0-0 и некоторую точку А внутри жидкости, ле-
жащую в этой плоскости. Используя уравнение (15) выразим давле-
ние в точке А
10
zgpp
А
⋅
⋅
+
=
ρ
,
или
20
zgpp
А
⋅
⋅
+
=
ρ
.
Следовательно
21
zz = .
Таким образом, в сообщающихся сосудах, находящихся под оди-
наковым давлением и заполненных однородной жидкостью, уровни
жидкости располагаются на одной высоте независимо от формы
сосудов. Этот принцип используется для измерения уровня жидкости
в закрытых аппаратах при помощи стеклянных трубок.
Рис. 8. Условия равновесия в сообщающихся сосудах: а - однородная
жидкость; б - разнородные несмешивающиеся жидкости.
Если сообщающиеся сосуды заполнены двумя несмешивающи-
мися жидкостями, имеющими разные плотности
1
ρ
и
2
ρ
(рис. 8, б),
получим
110
zgpp
А
⋅
⋅
+
=
ρ
,
или
220
zgpp
А
⋅
⋅
+
=
ρ
.
б
)
A
z
2
0 0
p
0
p
0
z
1
а
)
A
z
2
0
0
p
0
p
0
z
1
29
Тогда
2211
zz
⋅
=
⋅
ρ
ρ
,
(16)
или
1
2
2
1
ρ
ρ
=
z
z
.
Следовательно, в сообщающихся сосудах высоты уровней раз-
нородных жидкостей обратно пропорциональны плотностям этих
жидкостей.
Если сосуды заполнены одной жидкостью, но давления над
уровнем жидкости в них неодинаковы и равны
1
p и
2
p , то
2211
zgpzgp
⋅
⋅
+
=
⋅
⋅
+
ρ
ρ
,
откуда разность уровней жидкости в сосудах
g
pp
zz
⋅
−
=−
ρ
21
12
.
(17)
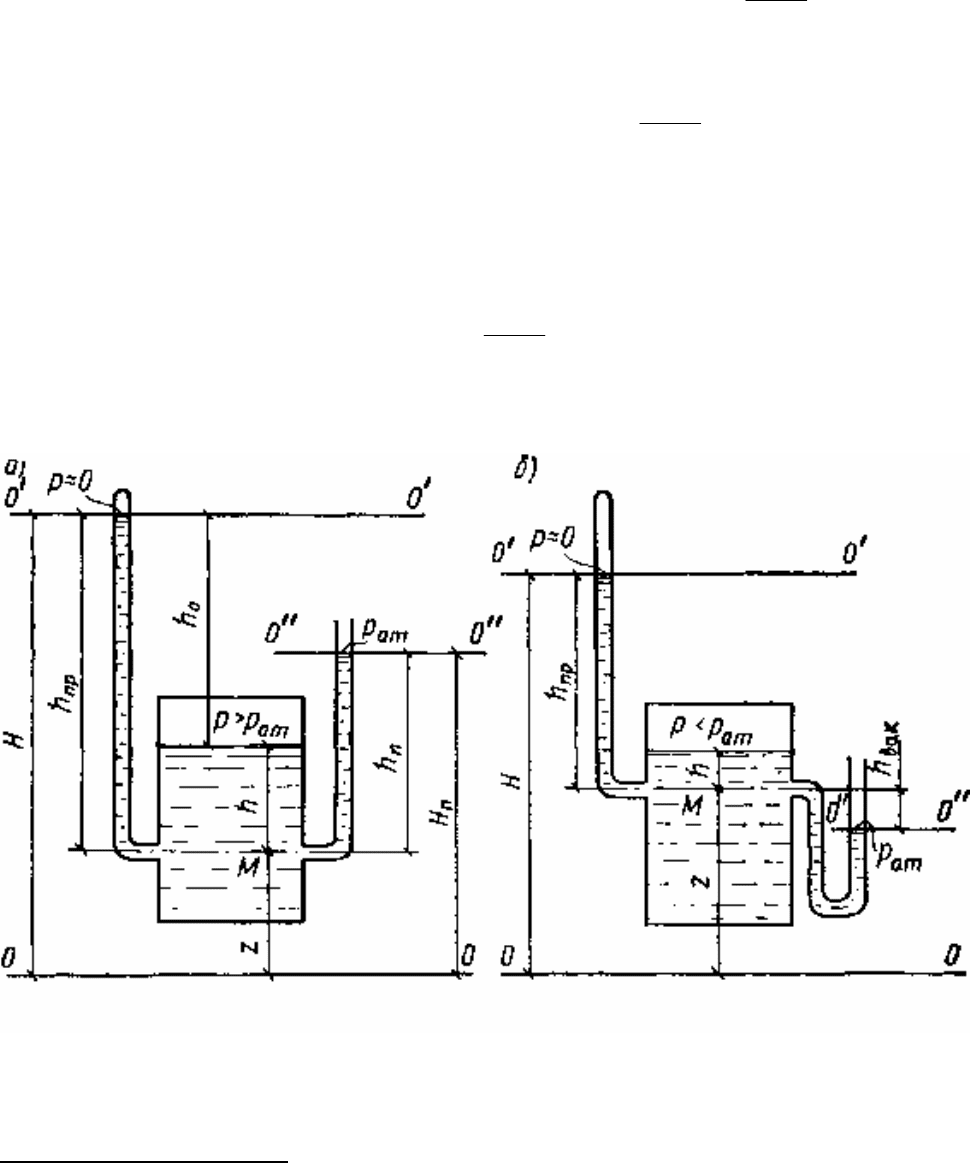
Полученное уравнение используют при измерениях давлений или
разностей давлений между различными точками жидкости с помощью
дифференциальных U-образных манометров (рис. 9).
Рис. 9. Применение принципа сообщающихся сосудов
для измерения давления жидкости.
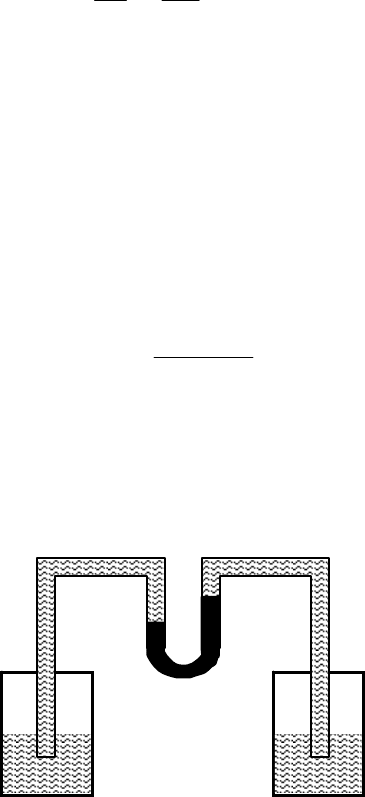
Определение высоты гидравлического затвора.
Условия рав-
новесия жидкостей в сообщающихся сосудах можно использовать
для определения высоты гидравлического затвора в различных аппа-
ратах. Например, если в емкости (рис. 10) находится смесь жидкостей
с различной плотностью
1
ρ
и
2
ρ
(эмульсия), давление над жидкостью
внутри резервуара и на выходе из затвора одинаково, граница раздела
фаз поддерживается на стыке цилиндрической и конической частей
емкости, то необходимая высота гидравлического затвора, согласно
уравнению (16)
30
2
11
2
ρ
ρ
z
z
⋅
=
.
Рис. 10. К определению высоты гидравлического затвора.
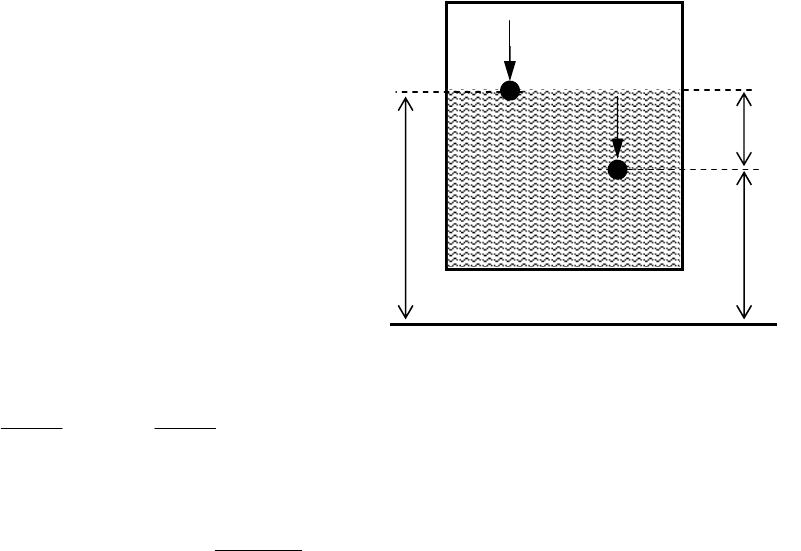
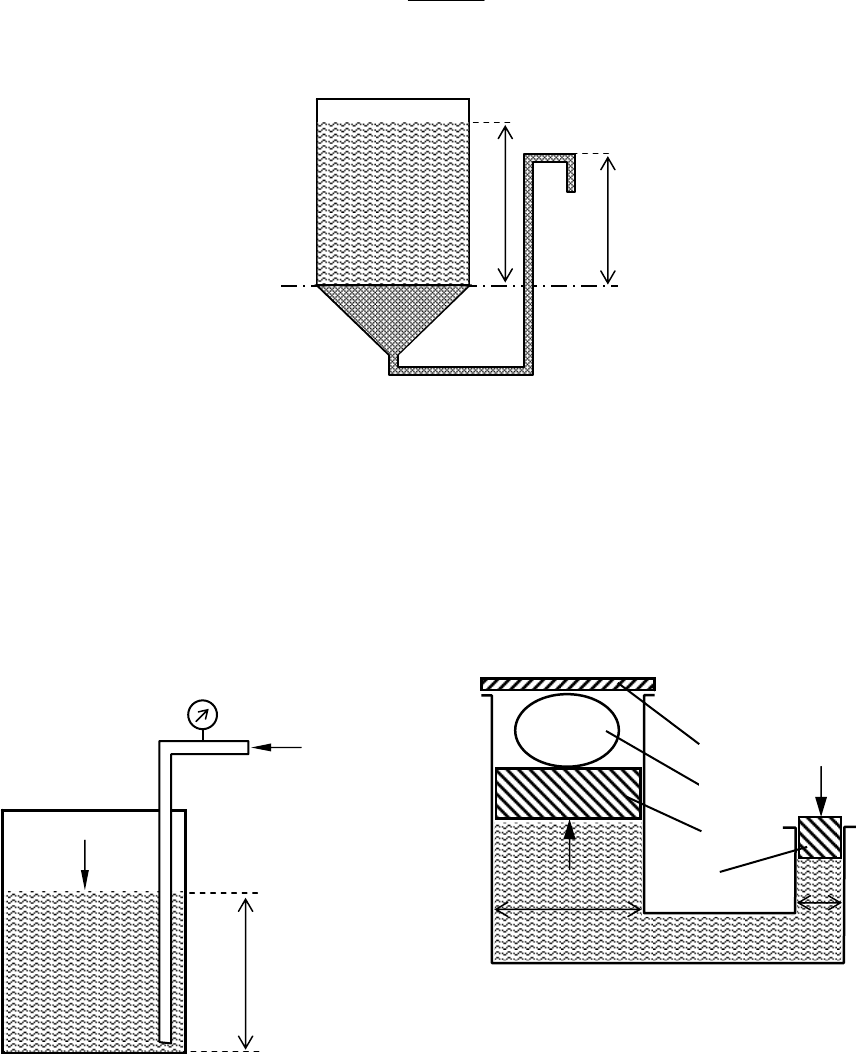
Пневматическое измерение количества жидкости.
Для изме-
рения объема жидкости в резервуарах, в них устанавливают трубку,
нижний конец которой доходит практически до днища резервуара
(рис. 11).
Через верхний конец трубы в емкость подают сжатый газ, по-
степенно повышая его давление. Когда газ преодолеет сопротивление
столба жидкости
h
g
⋅⋅
ρ
и давление
0
p на поверхность жидкости в
резервуаре, он начнет барботировать (пробулькивать) через жид-
кость. При этом давление газа
г
p
, замеряемое манометром, переста-
z
1
0
0
z
2
Рис. 11. Пневматический
изме
р
итель
ур
овня жидкости.
p
0
p
г
h
Рис. 12. Схема гидравлического
пресса: 1 - поршень малого диа-
метра; 2 - поршень большого диа-
метра; 3 - обрабатываемый матери-
ал;
4
- неподви
ж
ная плита.
F
1
d
2
F
2
1
2
3
4
d
1
p
