Щелкачев В.Н. Основы и приложения теории неустановившейся фильтрации: Часть 1
Подождите немного. Документ загружается.


Глава 2
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПРОСТЕЙШИХ
ОДНОМЕРНЫХ ПОТОКОВ.
ПРЕОБРАЗОВАНИЯ КООРДИНАТ
§ 1. Характеристики простейших одномерных потоков
и замечания о целесообразности
преобразования координат
Если в любой точке пространства все характеристики фильт
рационного потока (например, давление, скорость фильтрации,
плотность жидкости и т.д.) зависят не более чем от одной
координаты этой точки*, то такой поток называется одномерным.
Существуют три типа простейших одномерных потоков, в
которых траектории частиц жидкости прямолинейны:
1. Прямолинейно-параллельный.
2. Плоско-радиальный или же прямолинейно-осесимметричный.
3. Сферический радиальный.
Известно, что в неустановившихся потоках линии тока могут,
вообще говоря, не совпадать с траекториями. Однако в простейших
одномерных потоках, даже если они неустановившиеся, линии тока
всегда совпадают с прямолинейными траекториями.
В прямолинейно-параллельном потоке все траектории не только
прямолинейны, но и параллельны друг другу (см. рис. 2.1).
В условиях этого потока естественно совместить ось координат,
например ось х, с одной из траекторий. Тогда в любой точке
неустановившегося ротока давление (как и другие характеристики
потока) будет функцией только координаты х и времени t:
p = p (x ,t ). (2.1)
Поэтому уравнение изобары имеет вид:
х = const. (2.2)
В конце § 8 главы 1 было указано, что при решении задач теории упругого
режима, связанных с исследованием перераспределения давления, можно не учиты
вать влияния силы тяжести.

Рис. 2.1. Траектории и изобары в прямолинейно-параллельном потоке
Для пространственных задач это уравнение соответствует
семейству плоскостей, перпендикулярных оси х. Для плоских задач
(считая, что плоскость рис. 2.1 совмещена с плоскостью течения)
уравнение (2.2) определяет семейство прямых, перпендикулярных
оси х.
В осесимметричном потоке, как это следует из названия, имеется
полная симметрия потока по отношению к некоторой оси. Не
всякий осесимметричный поток является одномерным, но прямо
линейно-осесимметричный поток одномерен. Движение жидкости
в прямолинейно-осесимметричном потоке определяется следующи
ми свойствами:
1. Можно считать, что все частицы жидкости движутся только
в плоскостях, перпендикулярных одной и той же прямой — оси
симметрии потока.
2. В каждой плоскости течения траекториями служат прямые
линии, либо радиально сходящиеся к одному центру (точке
пересечения оси симметрии с плоскостью течения), либо радиально
расходящиеся от него.
На рис. 2.2,а изображено плоское сечение прямолинейно-осе
симметричного потока, перпендикулярное оси симметрии. На
рис. 2.2,6 изображено сечение того же потока плоскостью, прохо
дящей через ось симметрии.
В условиях плоской задачи прямолинейно-осесимметричный
поток обычно называют плоско-радиальным, причем тогда говорят
о симметрии такого потока по отношению к центру на плоскости
течения (см.рис.2.2,а).
В прямолинейно-осесимметричном или плоско-радиальном по
токе все его характеристики в какой-либо точке зависят от одной
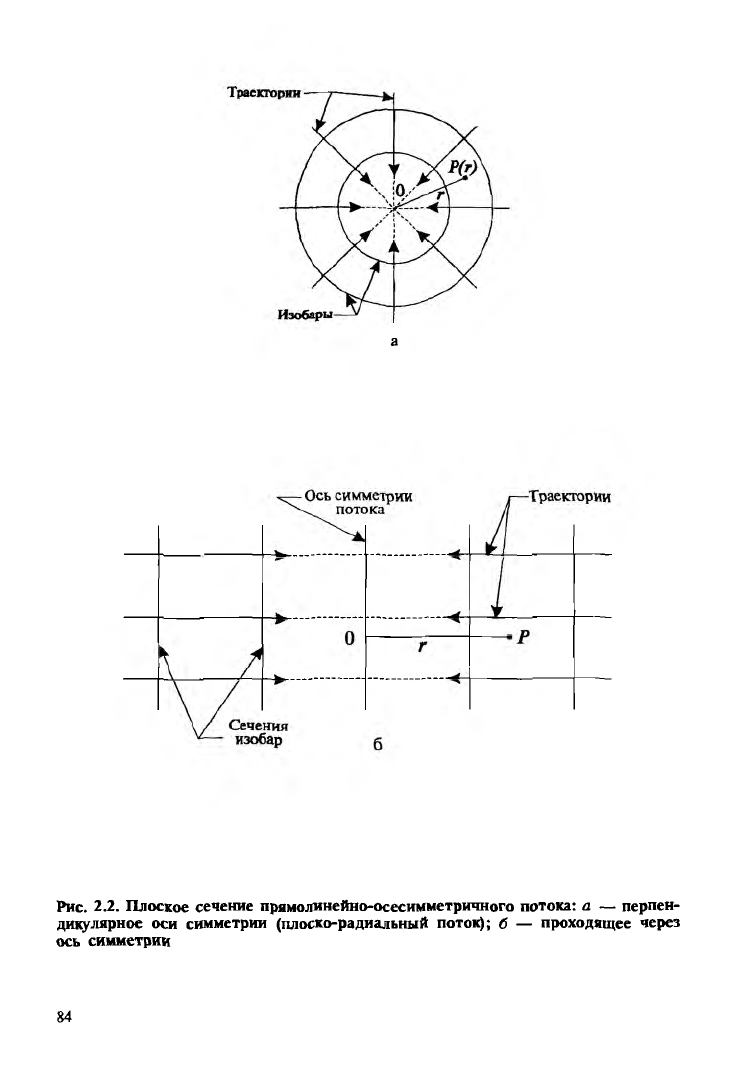
Рис. 2.2. Плоское сечение прямолинейно-осесимметричного потока: а — перпен-
дтдглярное оси симметрии (плоско-радиальный поток); б — проходящее через
ось симметрии

координаты этой точки — полярного радиуса л Следовательно, дав
ление в любой точке нестационарного потока рассматриваемого ти
па зависит только от двух переменных:
p = p (r ,t ). (2.3)
Уравнение изобары имеет вид:
г = const. (2.4)
На основании уравнения (2.4) можно утверждать (это очевидно
и из физических соображений), что для условий пространственных
задач изобарами служат поверхности коаксиальных цилиндров, а
для условий плоских задач — концентричные окружности.
В сферическом радиальном потоке имеется пространственная
симметрия относительно некоторого центра, причем все частицы
жидкости движутся по радиусам к некоторому центру или от него.
Рис. 2.2,а можно рассматривать как изображение сечения сфери
ческого радиального потока любой плоскостью, проходящей через
центр симметрии. Для этого потока остаются в силе уравнения
(2.3) и (2.4), но изобарами служат поверхности концентричных сфер.
Так как в прямолинейных одномерных потоках давление зависит
лишь от одной координаты (см. уравнения (2.1) и (2.3), то
дифференциальные уравнения пьезопроводности, соответствующие
этим потокам, должны быть проще, чем в общем случае. Упрощение
дифференциального уравнения пьезопроводности достигается вы
бором системы координат, однозначно предопределяемых особен
ностями каждого из трех простейших одномерных потоков (см. по
этому поводу § 2—5 данной главы). В § 6 этой же главы
рассматривается общий случай преобразования координат.
§ 2. Дифференциальное уравнение пьезопроводности
для прямолинейно-параллельного потока
Как уже было пояснено в предыдущем параграфе, в случае
неустановившегося прямолинейно-параллельного потока, направ
ленного, например, вдоль оси дс, давление является функцией
только одной координаты х и времени t (см. равенство (2.1) и
рис. 2.1). Поэтому в выражении лапласиана (1.46) остается только
одна производная по координате х; дифференциальное уравнение
пьезопроводности (1.44) или (1.45) упрощается и принимает вид:

д 2р _ 1 Эр
Эх2 к Эt '
(2.5)
Если первая производная равная алгебраическому значению
градиента давления в условиях прямолинейно-параллельного потока,
была бы величиной постоянной, то, конечно, вторая производная
равнялась бы нулю, и на основании равенства (2.5) можно было
dx
бы утверждать, что давление р не зависит от времени t. Учитывая это,
некоторые авторы так характеризуют неустановившееся поле давле
ния: в данной точке поля давление изменяется со временем только в
том случае, когда градиенты давления оказываются различными в
направлении потока с двух сторон от любой заданной точки (т.е. когда
пьезометрические линии непрямолинейны). Последняя формулиров
ка, как было выше пояснено, оказывается совершенно правильной для
прямолинейно-параллельного потока. Однако совершенно недопусти
мо, как это делают некоторые авторы, применять только что приве
денную формулировку для характеристики любого неустановившего
ся поля давления. Из подземной гидравлики известно, что, например,
в условиях плоско-радиального потока численные значения градиен
тов давления в направлении потока с двух сторон от любой заданной
точки различны (т.е. пьезометрические линии непрямолинейны) даже
в том случае, если поток установившийся.
§ 3. Дифференциальное уравнение пьезопроводности
для плоско-радиального потока
В условиях неустановившегося плоско-радиального (прямоли
нейно-осесимметричного) потока давление в любой точке зависит
только от ее полярного радиуса г и от времени (см. равенство (2.3)
и рис. 2.2). В этих условиях для решения пространственных задач
удобно использовать цилиндрические координаты г, <р , z, связанные
с декартовыми координатами х> у, z следующими соотношения-
ми*(см.рис. 2.3):
*
На рис. 2.3 и 2.4 декартова система координат повернута по отношению к той,
которая была изображена на рис. 2.1 и чаще всего используется в данной книге. Это
сделано для того, чтобы получить общепринятые формулы преобразования декар
товых координат в сферические и цилиндрические, совмещая ось z с вертикалью,
как это привычно при изображении системы цилиндрических координат. ,
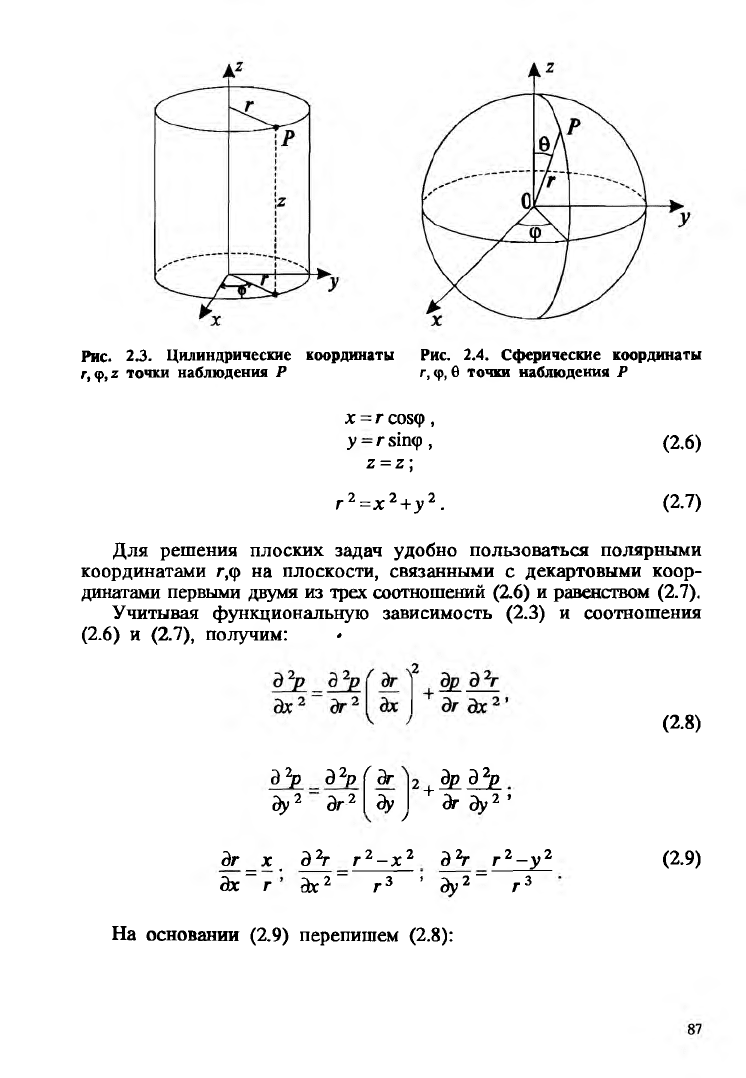
Рис. 23. Цилиндрические координаты Рис. 2.4. Сферические координаты
г, ф, z точки наблюдения Р г, <р, 0 точки наблюдения Р
x = r cos<p,
у -г sincp,
z = z;
(2.6)
r 2= x 2+ y 2.
(2.7)
Для решения плоских задач удобно пользоваться полярными
координатами г,<р на плоскости, связанными с декартовыми коор
динатами первыми двумя из трех соотношений (2.6) и равенством (2.7).
Учитывая функциональную зависимость (2.3) и соотношения
(2.6) и (2.7), получим: -
(2.8)
Э^р д2р ( дг др 8 2р
ду 2 Эг 2 Эу ^ + Эг Эу 2 ’
Эг=х . Э У _г2-х 2, д 2г _ г 2- у 2
Эх г дх2 г3 * Эу2 г3
(2.9)
На основании (2.9) перепишем (2.8):

Э 2р Э 2р х 2 др г 2- х 2
дхг ~ д г2 г 2 + Ъг г 3 ’
(2.10)
= , <>Б-Г--У.2
ду 2 дг2 г 2 дг г 3
Пользуясь равенствами (2.7), (2.10) и (1.46), можем записать
выражение лапласиана давления после перехода от декартовых
координат к цилиндрическим или к плоским полярным координатам,
но только для условий прямолинейно-осесимметричного или
плоско-радиального потока (когда р не зависит ни от ф, ни от z):
х 2+ у 2 др 2 гг ~ х г - у г
Эг2 г2 Эг г 3
или же
= + (2.11)
д г 2 Г д г
Поэтому дифференциальное уравнение пьезопроводности (1.44)
или (1.45) для прямолинейно-осесимметричного или плоско-ради
ального потока принимает следующий вид:
= (2.12)
Эг2 г Эг к dt *
§ 4. Дифференциальное уравнение пьезопроводности
для сферического радиального потока
В сферическом радиальном потоке, в котором давление в любой
точке зависит только от ее полярного радиуса г и от времени
(см. равенство (2.3), удобно использовать сферические координаты
г, <р, 9, связанные с декартовыми следующими соотношениями
(см.рис. 2.4):
(2.13)
Jt=rsin0cos<p,
y = rsin9sm<p,
z-rcosO;

Учитывая равенство (2.3) и соотношения (2.13) и (2.14), получаем
те же равенства (2.8)— (2.10), какие были выведены в предыдущем
параграфе, откуда
2 Ду г ~
Э^ х г + у г + г 2 др Зг2-лг2-у г-22
дг2 г 2 + Эг г3
Эг2 г Эг
(2.15)
Поэтому дифференциальное уравнение пьезопроводности (1.44)
или (1.45) для сферического радиального потока принимает
следующий вид:
Подчеркнем, что уравнение (2.16) отличается от дифференци
ального уравнения (2.12) для плоско-радиального потока лишь
коэффициентом 2 при втором слагаемом в левой части.
§ 5. Общий вид дифференциального уравнения
пьезопроводности в условиях одномерного потока
в многомерном пространстве
Обобщая изложенное в § 1— 4 данной главы, делаем вывод,
что дифференциальное уравнение пьезопроводности для любого
из трех рассмотренных простейших одномерных потоков может
быть записано в следующей единой форме:
Э 2р 2 др 1 др
Эг2 + г Эг к Эг '
(2.16)

В этом уравнении величину | следует считать той единственной
координатой, которая необходима для определения положения
точки в условиях любого из трех простейших одномерных потоков;
а — постоянная величина.
Для прямолинейно-параллельного потока (т.е. для одномерного потока
в пространстве одного измерения) надо в уравнении (2.17) принять
а = 0, % = х. (2.18)
Для плоско-радиального потока (т.е. для одномерного потока
в пространстве двух измерений)
а=1, 1 = г. (2.19)
Для сферического радиального потока (т.е. для одномерного
потока в пространстве трех измерений)
а = 2, | = г. (2.20)
Прямолинейно-параллельный, плоско-радиальный и сфериче
ский радиальный потоки допустимо рассматривать как простейшие
одномерные потоки в пространствах соответственно одного, двух
и трех измерений (число измерений* пространства на единицу
больше числа а).
Допустимо считать*, что уравнение (2.17) характеризует про
стейший одномерный поток в многомерном пространстве ( а + 1 )
измерений, где а = 0,1,2,3,....
Необходимость рассмотрения простейших одномерных потоков
в многомерных пространствах возникает во многих задачах мате
матической физики, в теории турбулентности, в теории теплопро
водности, в подземной гидродинамике и т.д. (см., например, [891],
[424], [441], [527], [761], [762], [118]).
Заметим, что дифференциальное уравнение (2.17) можно
переписать еще в следующем виде:
J__3
Iе 31
■ if. <22|>
2
Конечно, можно непосредственно доказать, что выражение лапласиана А р
для одномерного потока в пространстве (а + 1) измерений действительно совпадает
с выражением левой части уравнения (2.17).

§ 6. Преобразование уравнения пьезопроводности
при использовании любых криволинейных
координат
Положение точки в фильтрационном потоке не обязательно
определять с помощью декартовых координат х, у, z, но можно
воспользоваться любой системой ортогональных (для удобства)
криволинейных координат q
1
, q 2, Я з * Будем считать известными
выражения каждой из декартовых координат в функции криво
линейных координат:
*=*(<? 1 ,02.9з ).
У=У(Я I ,Яг,Яз), (2,22)
z = z(qi,q2,q3)-
Уравнение теплопроводности, вполне аналогичное уравнению
пьезопроводности, впервые было в общем виде выражено в
криволинейных координатах в 1833 г. Ламе [894]. Для этого
Ламе воспользовался функциональными зависимостями (2.22) и
с их помощью преобразовал дифференциальное уравнение (1.62),
выраженное в декартовых координатах, к криволинейным. Только
что указанный естественный и, по идее, весьма простой метод
Ламе требует проведения трудоемких выкладок. Уиллиам Томсон
(лорд Кельвин) отметил этот недостаток (громоздкость) метода
Ламе и предложил иной метод вывода дифференциального
уравнения теплопроводности в криволинейных координатах. Томсон
подчеркнул, что он разработал свой метод в 1850 г., но опуб
ликовал его несколько позже. Воспроизведем здесь метод Том
сона [966], но излагать этот метод будем на языке подземной
гидродинамики, т.е. применительно к выводу дифференциального
уравнения пьезопроводности.
Идея метода Томсона состоит в том, что сначала выводится
в криволинейных координатах уравнение неразрывности, а затем
уравнение пьезопроводности получается из него на основе закона
фильтрации Дарси и уравнений состояния жидкости и пористой
среды. Следовательно, Томсон сохраняет метод Эйлера, изло
женный в § 2 главы 1, но только выбор элементарного объема
связан у Томсона с системой криволинейных координат.
На рис. 2.5а изображена произвольная точка Р в области
пространства, занятой фильтрационным потоком. Положение точ
ки Р однозначно определяется тремя криволинейными коорди-
