Савина Н.В. Применение теории вероятности и методов оптимизации в системах электроснабжения
Подождите немного. Документ загружается.


211
тогда нормированную корреляционную функцию можно представить через
(
)
x
S
ω
:
() ()
∫
∞
=
0
cos ωωτωτ
χ
χ
dSR
и, наоборот,
() ()
∫
∞
=
0
cos
2
τωττ
π
ω
χ
χ
dRS ,
а
()
∫
∞
=
0
1ωω
χ
dS .
5.5. Применение случайных процессов в электроэнергетике.
Теория случайных процессов сейчас находит широкое применение в
электроэнергетике как на этапе проектирования, так и в эксплуатации.
Рассмотрим использование модели «Случайный процесс» для описания
электрических нагрузок.
Количественная информация об электрических нагрузках является
основой рационального решения практически всего комплекса вопросов,
связанных с эксплуатацией электрических сетей и систем электроснабжения.
Изменчивость нагрузок не дает возможности определения
закономерности их изменения только при представлении их случайными
величинами.
При решениях различных задач используется различное количество
информации о нагрузке. Так, при планировании развития сетей, нагрузки
потребителей могут задаваться детерминированно. При расчетах показателей
функциональной надежности электрических систем и систем
электроснабжения, оптимизации режимов, их краткосрочном планировании в
эксплуатации, разработке алгоритма управления или регулирования, нагрузка
задается случайным процессом со всеми его характеристиками. Для
определения потерь в элементе сети за некоторый интервал времени нет
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

212
необходимости в информации о связи и последовательности ординат процесса,
важна лишь частота появления тех или иных значений нагрузки за этот
интервал. А вот для расчета температурных режимов изоляции необходимо
знать последовательность появления этих значений во времени из-за
инерционности процессов нагрева. Аналогично при оценке показателей
качества электроэнергии по интегральным характеристикам при отклонении
напряжения нам не важно знать последовательность и связь между ординатами,
но при определении дозы фликера или при выборе рационального закона
регулирования напряжения без этого не обойтись. В первом случае нагрузка
описывается моделью случайных величин, а во втором – случайных процессов.
Интервал дискретизации зависит от решаемой задачи и от характера
электропотребления.
Как мы отметили, случайный процесс характеризуется математическим
ожиданием или функцией математического ожидания и корреляционной
функцией, отражающей связь между ординатами процесса. Анализируя АКФ,
можно сделать вывод о ее свойствах, эргодичности и стационарности, что
требуется для выявления количества необходимой информации о нагрузке.
В практических расчетах корреляционные функции аппроксимируются
следующими выражениями:
(
)
12
Rcec
ατ
τ
−
=+
;
(
)
-бф
1
о
R
ф =cecosщф
;
(
)
-бф
1
о 2
R
ф =cecosщф+c
,
где
12
c,c,,
αω
– постоянные величины, получаемые в результате
статистической обработки;
α - коэффициент затухания;
о
ω
- собственная частота.
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com
213
При эргодических процессах
12
1;0
cc
==
. Опыт статистических
исследований показывает, что в сетях общего назначения в часы максимума
нагрузок энергосистем корреляционная функция изменяется по
экспоненциальному закону, для полных суток – по экспоненциально-
косинусному закону.
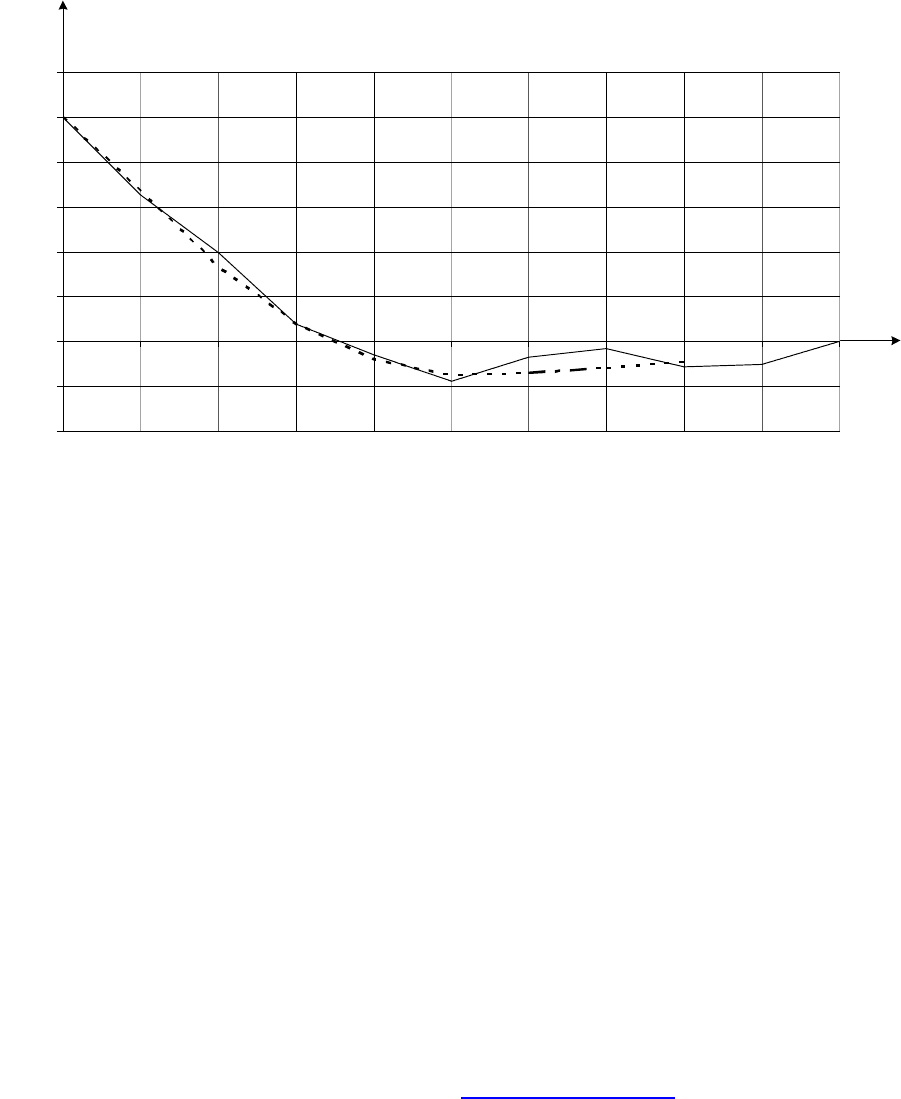
Пример. В результате статистических исследований электрической
нагрузки потребителя был получен график нормированной корреляционной
функции (НКФ), приведенный на рис. 75.
,
мин
τ
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
1.2
0 30 60 90 120 150 180 210 240 270 300
(
)
0.01
X
Recos0.0151
τ
ττ
−
=
(
)
X
R
τ
Рис. 75
Необходимо аппроксимировать данную НКФ.
Исследуемый случайный процесс является эргодическим, т.к. связь
между сечениями убывает во времени. Для аппроксимации НКФ выберем
следующую математическую модель:
(
)
-
бф
R
ф =ecosщф
xo
.
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com
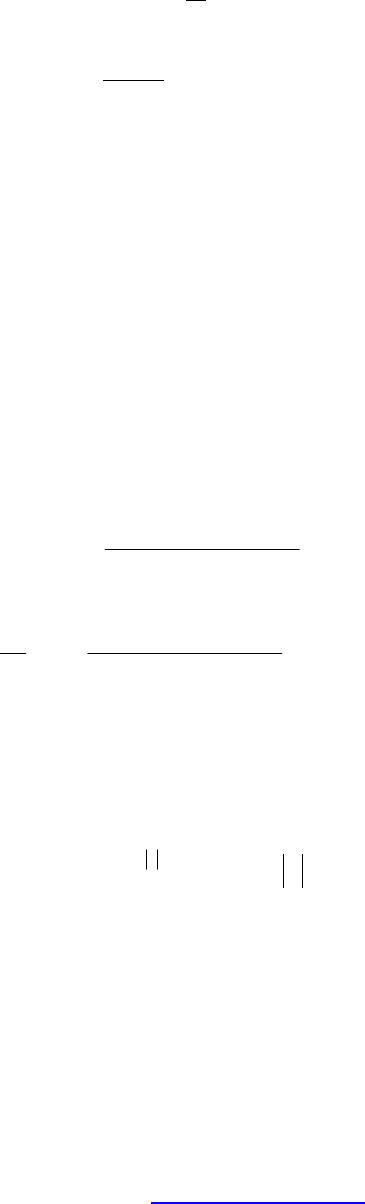
214
Для определения коэффициентов α и
o
ω
выполним следующие операции:
в точке абсцисс
1
ф =104
мин
, а
(
)
х
R
ф =0
. Тогда
1
-бф
1
е cos
ф =0
,
Так как
1
-бф
е 0
≠
, то
о 1
cos
щф=0
.
Отсюда
о 1
2
π
ωτ
=
,
0,0151
2104
о
π
ω ==
⋅
.
Точка первого минимума
(
)
х
R
τ
соответствует
2
τ
=150 мин, а само
значение
(
)
0,14
х
R τ =− .
Тогда
2
2
cos0,14
о
е
ατ
ωτ
−
=−
или
( )
2
0,14
cos0,0151150
е
ατ−
=−
⋅
,
( )
2
10,14
ln0,01
cos0,0151150
α
τ
=−−=
⋅
.
Следовательно, аналитическое выражение для данной НКФ будет иметь
вид:
(
)
0.01
cos0,0151
x
Re
τ
ττ
−
= .
В общем виде модель случайного процесса комплексной токовой
нагрузки потребителя представлена следующим выражением:
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com
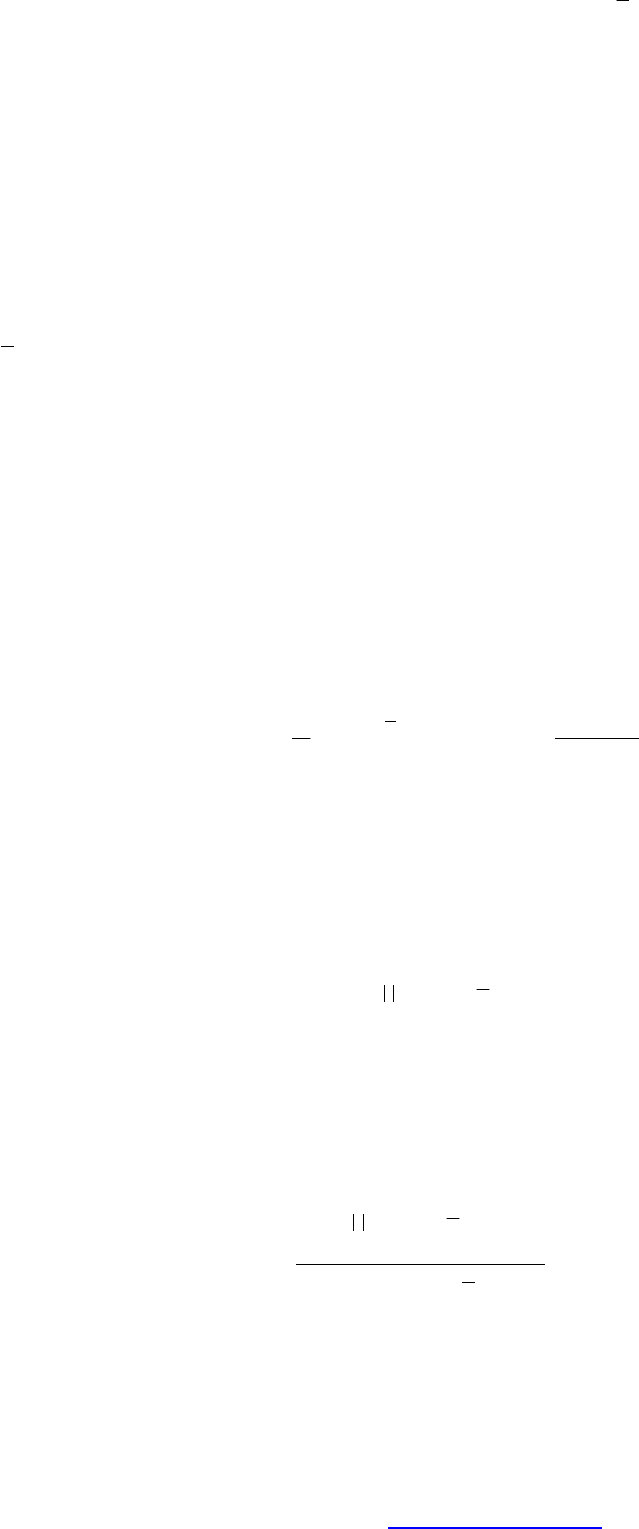
215
() ( ) ()
0
1
cos
Г
N
T
ItItItI
ννν
ν
ωϕ
=
=+++
∑
,
где
,
,
I
ννν
ωϕ
– соответственно усредненная амплитуда, частота и усредненный
фазовый сдвиг ν-ой гармонической составляющей;
(
)
tI
0
– стационарный случайный процесс с нулевым математическим
ожиданием, стандартным отклонением
0
σ
и экспоненциальной КФ,
характеризуемой коэффициентом затухания α;
T
I
– среднее значение нагрузки за рассматриваемый интервал
времени;
Г
N
– число учитываемых гармоник. Для электрических нагрузок, как
правило
Г
N
= 4÷5.
Спектральная плотность процесса
( ) ( )
2
2
0
2
2
1
1
0,5,
Г
N
о
SI
ν
ν
ν
α
ωδωωσ
π
αω
=
=−+
+
∑
где
(
)
ν
δωω
− - дельта функция корреляционной функции, соответствующая
этой спектральной плотности
(
)
S
ω
:
()
22
0
1
0,5cos
N
Ке
ατ
νν
τ
ν
σωτ
−
=
+Ι
∑
.
Нормированная корреляционная функция описывается выражением:
()
22
0
1
22
0
1
0,5cos
0,5
N
N
е
R
ατ
νν
ν
τ
ν
ν
σωτ
σ
−
=
=
+Ι
=
+Ι
∑
∑
.
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

216
Математическое ожидание случайного процесса:
() ( ) ()
0
1
00
11
cos
Г
ТТ
N
ТТ
ItdtIttТdt
ТТ
ννν
ν
ωϕ
=
Ι==+=Ι+=Ι
∑
∫∫
.
Дисперсия случайного процесса
() ()
2222
0
1
0
1
0,5
Г
Т
N
Dtdt
Т
ν
ν
σ
=
Ι=Ι−Ι=Ι+
∑
∫
.
Время корреляции
1
к
τ
α
=
.
Если изменение активной мощности во времени описывается
стационарным и эргодическим процессом
{
(
)
}
Р t
, то вероятностные
характеристики вычисляются по одной исходной
(
)
Р t
реализации за
достаточно продолжительный период времени Т.
Средняя нагрузка исходного
(
)
Р t
графика:
()
0
1
lim
Т
ср
Т
РРtdt
Т
→∞
=
∫
.
Среднеквадратическая нагрузка исходного
(
)
Р t
графика:
()
2
0
1
lim
Т
э
Т
РРtdt
Т
→∞
=
∫
.
Дисперсия нагрузки исходного
(
)
Р t
графика:
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com
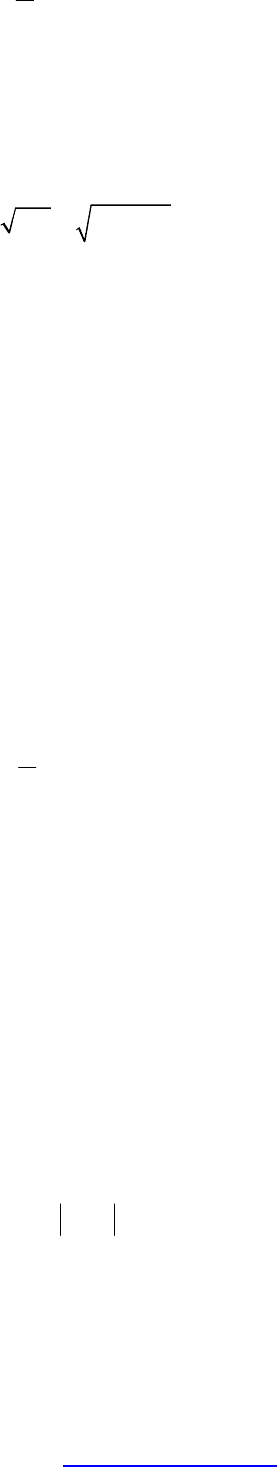
217
()
2
0
1
lim
Т
ср
Т
D
РРtРdt
Т
→∞
=−
∫
.
Дисперсия, средняя и среднеквадратическая нагрузки исходного графика
связаны между собой следующим соотношением:
22
эср
DP
РР
σ ==−.
Все моментные характеристики стационарного и эргодического
случайного процесса
{
(
)
}
Р t
представляют неслучайные величины и
изображаются в виде неизменных во времени прямых линий.
Для стационарных и эргодических случайных процессов корреляционная
функция не зависит от моментов времени
1
t
и
2
t
, а зависит только от
временного сдвига
12
tt
τ
=−
между ординатами
(
)
Р t
графика и вычисляется по
одной реализации за достаточно продолжительный период времени Т:
()
() ( )
0
1
lim
Т
Т
КРtPtdt
Т
τ
τ
→∞
=+
∫
.
Количественной характеристикой вероятностной взаимосвязи между
ординатами стационарного и эргодического процесса
(
)
Р t
служит интервал
корреляции
к
Т
- постоянная времени корреляции.
Интервал корреляции
к
Т
определяется интегралом от модуля
нормированной корреляционной функции по выражению:
()
0
к
Т Rdt
τ
∞
=
∫
,
где
(
)
(
)
/
R
К DP
ττ= .
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

218
Ординаты графика нагрузки разделены между собой интервалом
времени
к
Т
τ
≤
, являются в среднем коррелированными (зависимыми).
При
3
к
Т
τ ≥ вероятностная взаимосвязь между значениями ординат
графика
(
)
Р t
практически затухает, а ординаты становятся независимыми друг
от друга.
Практическая значимость корреляционной функции как характеристики
взаимосвязи между ординатами случайного процесса на этом не
ограничивается. Важной особенностью корреляционной функции является то,
что для одного и того же момента времени
12
tt
=
(при
0
τ
=
) она обращается в
дисперсию исходного графика
(
)
Р t
нагрузки – случайную величину,
определяемую выражением:
(
)
22
0
эср
К DP РР
==− .
Отсюда следует практически важный вывод о том, что необходимость в
дисперсии, как отдельной характеристики случайного процесса
{
(
)
}
Р t
отпадает:
в качестве основных вероятностных характеристик стационарного и
эргодического случайного процесса
{
(
)
}
Р t
достаточно рассматривать его
математическое ожидание и корреляционную функцию.
Корреляционная функция случайного процесса
{
(
)
}
Р t
характеризует
взаимосвязь ординат графика нагрузки и определяет вероятностные
характеристики выбросов и провалов графика
(
)
Р t
нагрузки за заданный
уровень
у
Р
.
Пример. Для графика
(
)
Р t
нагрузки, изображенного на рис. 76,
вычислить основные характеристики:
(
)
,,,
срэрр
РРD иR
στ
.
Построить нормированную КФ.
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com
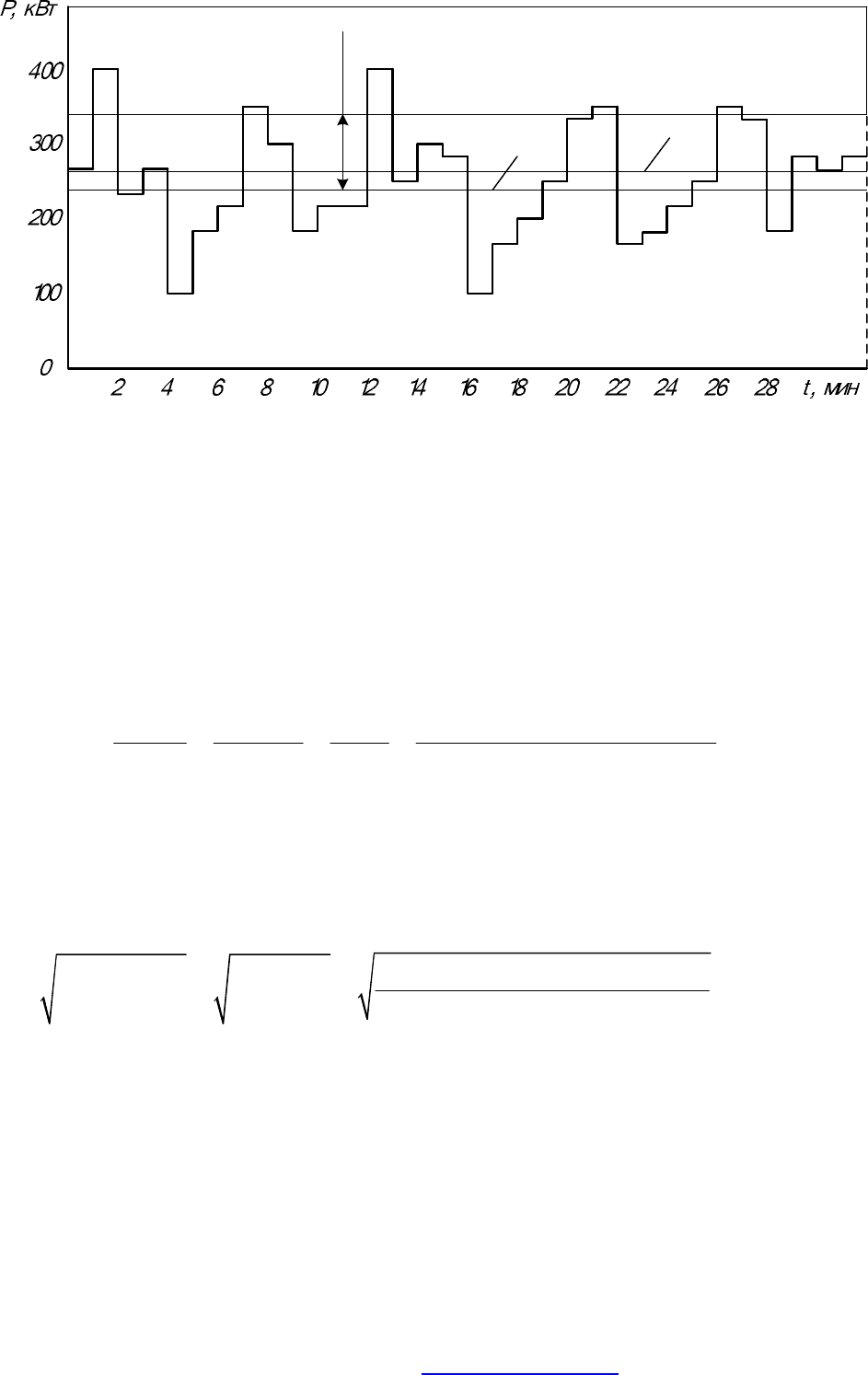
219
73
σ
=
ср
Р 256
=
э
Р 266
=
Рис. 76
График
(
)
Р t
нагрузки ступенчатый, длительность каждой ступени равна
t1
мин
∆
=
. Время наблюдения за графиком
Т 32мин
=
. Число ступеней
(ординат)
NT/t32/132
∆
===
. Среднее значение нагрузки за время Т:
NNN
iiiii
i1i1i1
ср
N
i
i1
Рt Р t Р
10021602...4002
Р 256кВт
Т N32
t
∆
∆
===
=
⋅+⋅++⋅
=====
∑∑∑
∑
.
Среднеквадратическое значение нагрузки за время Т:
222
NN
2
эiii
i1i1
10021602...4002
РРt/ТР/N266кВт
32
∆
==
⋅+⋅++⋅
====
∑∑
.
Дисперсия нагрузки:
22222
рэср
D
РР 2662565329кВт
=−=−= .
Среднеквадратическое значение нагрузки:
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com
220
рр
D532973
кВт
σ ===
.
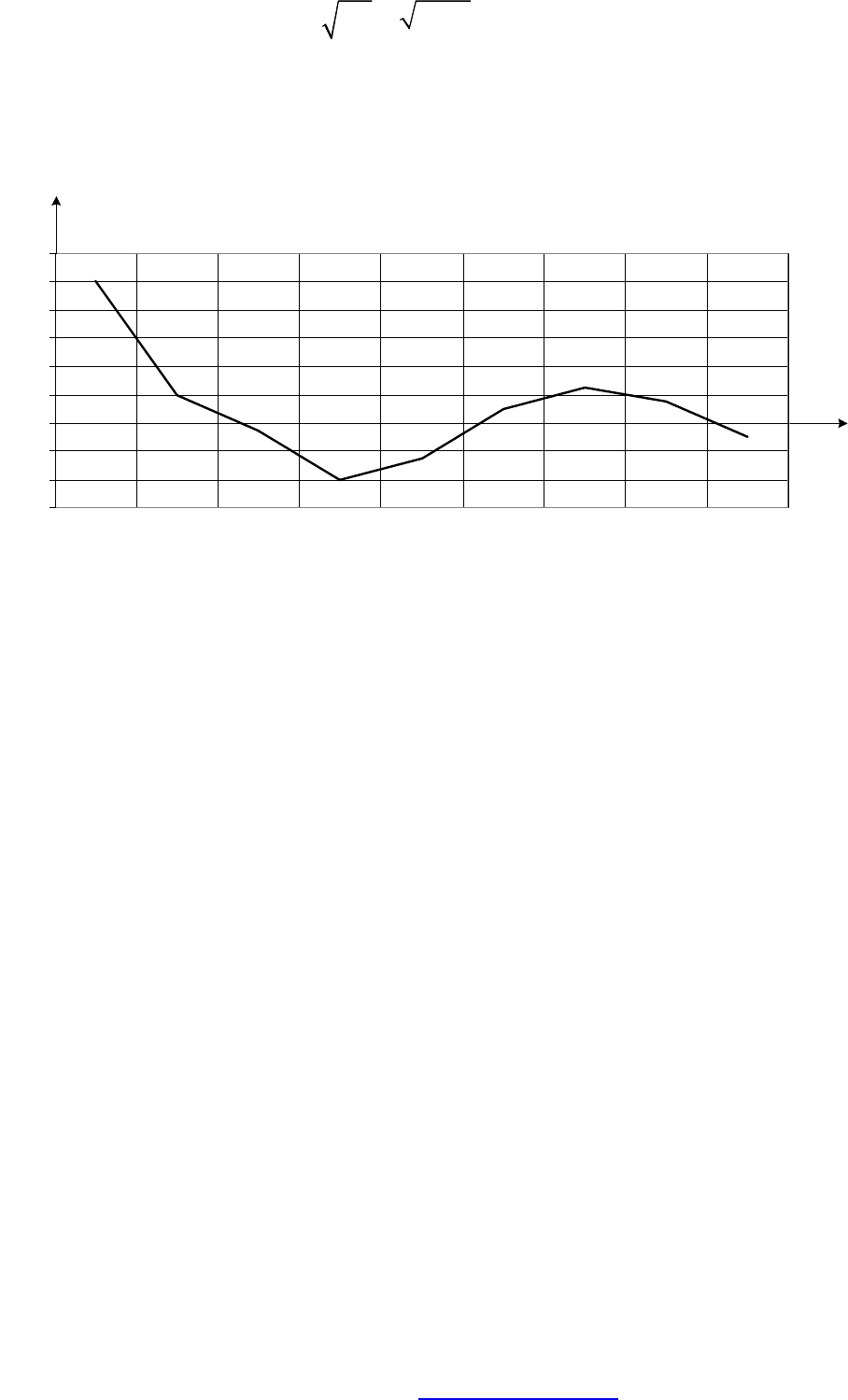
Вычисляются корреляционная и нормированная корреляционная функция
(НКФ). Результаты расчета представлены рис. 77.
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
1.2
0 1 2 3 4 5 6 7 8
,
мин
τ
(
)
R
τ
Рис. 77
Нормированная корреляционная функция имеет колебательный характер,
и ее аналитическое выражение может быть записано в виде:
(
)
0
r е cos
ατ
τωτ
−
= ,
где
0
,
αω
- соответственно коэффициент затухания и собственная частота НКФ.
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com
