Савина Н.В. Применение теории вероятности и методов оптимизации в системах электроснабжения
Подождите немного. Документ загружается.

201
5.3. Экспериментальное определение характеристик
случайного процесса
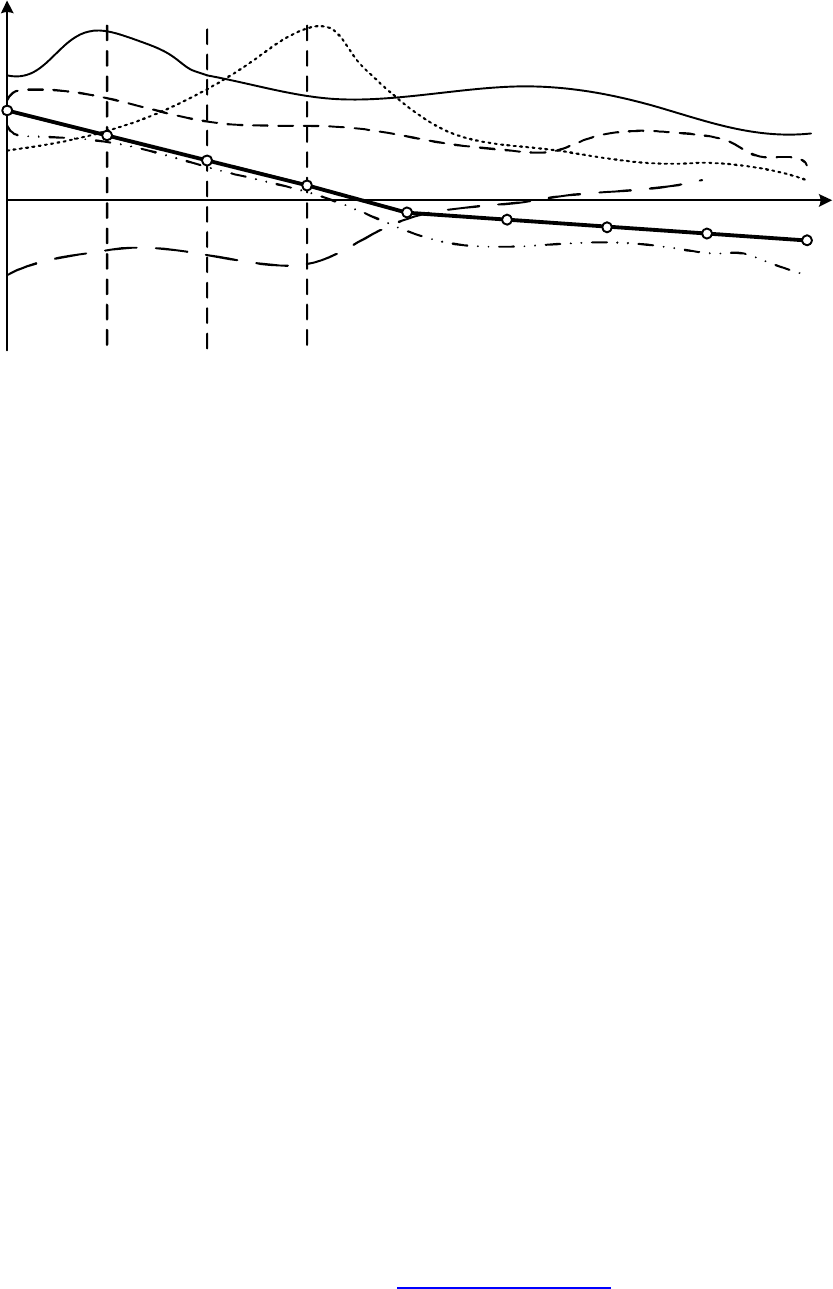
Случайные процессы в энергетике изучаются экспериментально. Пусть
над случайным процессом
(
)
tX произведено n независимых опытов и в
результате получено n реализаций случайного процесса (рис. 70).
(t)
χ
t
m(t)
χ
1
t
2
t
3
t
4
t
3
(t)
χ
1
(t)
χ
n
(t)
χ
2
(t)
χ
Рис. 70
Требуется найти оценки для характеристик случайного процесса:
(
)
(
)
(
)
,,,
mtDtKtt
χχχ
′
.
Для этого рассмотрим ряд сечений случайного процесса для моментов
времени
m
ttt ,...,,
21
и зарегистрируем значения, принятые
(
)
tX в эти моменты
времени. Каждому из моментов
1
t ,
2
t ,…,
m
t будет соответствовать n значений
случайного процесса.
Значения
1
t ,
2
t ,…,
m
t задаются равностоящими. Величины интервала
дискретизации выбираются, исходя из сущности рассматриваемого процесса и
поставленной задачи. Так, изучая изменение нагрузки во времени
электроприемников общего назначения, в качестве интервала дискретизации ∆t
обычно принимают 1 час или 0,5 часа. При исследовании резкопеременных
нагрузок интервал дискретизации составляет несколько секунд.
Достаточное время одной реализации равно:
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com
202
,
2
2
2
M
k
D
V
T
γ
τ
=
где V – коэффициент вариации;
K
τ
– время корреляции, то есть время затухания корреляционной
зависимости случайного процесса;
M
γ
– относительная погрешность при вычислении математического
ожидания,
()
,
0
∫
∞
= τττ dR
K
где
(
)
τ
R - нормированная корреляционная функция.
Зарегистрированные в результате измерений значения
(
)
tX заносятся в
таблицу, каждая строка которой соответствует определенной реализации, а
число столбцов равно числу опытных значений аргумента.
t
1
t
2
… t
i
t
k
t
m
x
1
(t) x
1
(t
1
) x
1
(t
2
) … x
1
(t
i
) х
1
(t
k
) х
1
(t
m
)
x
2
(t) x
2
(t
1
) x
2
(t
2
) … x
2
(t
i
) х
2
(t
k
) х
2
(t
m
)
… … … … … х
3
(t
k
) …
x
n
(t) x
n
(t
1
) x
n
(t
2
) … x
n
(t
i
) х
4
(t
k
) x
n
(t
m
)
Полученный материал представляет собой не что иное, как результаты n
опытов над системой m случайных величин:
(
)
(
)
(
)
12
,,...,
m
XtXtXt
и обрабатывается согласно правилам математической статистики. Прежде всего
находятся оценки математического ожидания:
( )
()
,
1
n
tx
tm
k
n
i
i
k
∑
=
=
χ
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

203
затем дисперсий:
( )
() ()
[
]
1
1
2
−
−
=
∑
=
n
tmtx
tD
n
i
kki
k
χ
χ
и, наконец, корреляционных моментов:
( )
( ) ( ) () ()
1
,
1
n
ikkill
i
kl
xtmtxtmt
Ktt
n
χχ
χ
=
−−
=
−
∑
.
После этого, пользуясь значениями
(
)
,
1
tm
χ
(
)
,
2
tm
χ
… ,
(
)
m
tm
χ
, строят
зависимость m
x
(t), аналогично поступают для дисперсий и корреляционных
функций.
5.4. Стационарность и эргодичность случайных процессов
В электроэнергетике часто встречаются случайные процессы,
протекающие во времени однородно и имеющие вид непрерывных случайных
колебаний вокруг некоторого случайного значения, причем ни средняя
амплитуда, ни характер этих колебаний не обнаруживают существенных
изменений с течением времени. Такие случайные процессы называются
стационарными. Пример – колебания напряжения в осветительной сети.
Стационарный процесс не имеет ни начала, ни конца, т.е. при его
исследовании можно выбрать в качестве начала отсчета любой момент
времени. Исследуя стационарный процесс на любом участке времени, мы
должны получить одни и те же его характеристики.
Нестационарные процессы имеют тенденцию развития во времени;
характеристики такого процесса зависят от начала отсчета, от времени.
Их примером может быть процесс затухания колебаний в
электрической цепи.
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

204
Случайный процесс называется стационарным, если все его
вероятностные характеристики не зависят от времени, то есть не меняются при
любом сдвиге аргументов по оси t. Это означает, что
(
)
constmtm
=
=
χχ
,
(
)
constDtD
=
=
χχ
.
Его корреляционная функция зависит не от положения t первого
аргумента на оси абсцисс, а от промежутка τ между первым и вторым
аргументами:
(
)
(
)
,Kttk
χ
χ
ττ
+= .
Следовательно, автокорреляционная функция стационарного
случайного процесса есть функция не двух, а всего одного аргумента и является
четной функцией
(
)
(
)
τ
τ
χχ
−
=
kk .
Важным свойством некоторых стационарных случайных процессов
является эргодичность. Эргодичность упрощает исследование, так как
позволяет перейти от усреднения по ансамблю реализаций к усреднению по
времени для одной реализации. То есть математическое ожидание
эргодического процесса можно найти не только по множеству реализаций, но и
по одной развернутой во времени реализации.
Если случайный процесс
(
)
tX обладает эргодичностью, то для него
среднее по времени на достаточно большом участке наблюдения приближенно
равно среднему по множеству наблюдений. Аналогично, для
χ
D и
χ
K .
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

205
Об эргодичности или неэргодичности случайного процесса можно
судить по виду его корреляционной функции, что показано на рис. 71.
K
τ
y
D
K(t)
χ
2
K(t)
Рис. 71
В эргодичном процессе АКФ
(
)
0
→
τ
K при
∞
→
τ
, то есть
корреляционная связь между значениями случайного процесса неограниченно
убывает по мере увеличения расстояния между ними.
Определение характеристик эргодического стационарного процесса
по одной реализации
Математическое ожидание эргодического стационарного случайного
процесса можно определить по одной реализации
()
T
0
1
mxtdt,
T
χ
=
∫
где T – период наблюдения;
(
)
tx – одна реализация случайного процесса
или приближенно
()
,
1
1
∑
=
=
n
i
i
tx
n
m
χ
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

206
где
i
t – середины интервалов дискретизации.
1
t
m
χ
2
t
3
t
t
∆
t
(
)
t
χ
Рис. 72
() ()( )
∫
−
+
−
≈
τ
χ
τ
τ
τ
T
dttxtx
T
k
0
1
oo
,
где τ – некоторое фиксированное значение – интервал дискретизации; τ = 0; ∆t;
2∆t и т.д.;
() ( )
,xtxt
τ
+
oo
– центрированные значения реализации случайного процесса,
равные
() () () ( ) ( ) ()
,
хх
xtxt
т txtxt т t
ττ=−+=+−
oo
или
()( )
∑
−
=
+
−
=
mn
i
mii
txtx
mnn
mT
k
1
1
o
o
χ
где tm
n
mT
∆==τ ;
t
∆
– длина участка.
m = 0; 1; 2; 3 …… S,
где S – значение m, при котором АКФ = 0 или совершает периодические
колебания вокруг 0.
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com
207
§ 5. Спектральное разложение стационарного процесса.
Спектральная плотность
Как мы уже отмечали, существует связь между характером
корреляционной функции и внутренней структурой соответствующего
случайного процесса. В зависимости от того, какие частоты и в каких
соотношениях преобладают в составе случайного процесса, его
корреляционная функция имеет тот или иной вид, то есть можно говорить о
спектральном составе случайного процесса.
Если какой-либо колебательный процесс представляется в виде суммы
гармонических колебаний различных частот, то спектром колебательного
процесса называется функция, описывающая распределение амплитуд по
различным частотам. Аналогично для случайного процесса – спектр
стационарного процесса будет описывать распределение дисперсий по
различным частотам.
Пусть задана корреляционная функция
(
)
(
)
,Kttk
χχ
ττ
+= , она четная
(
)
(
)
,
τ
τ
χ
−
=
kk а четную функцию можно разложить в ряд Фурье, пользуясь
четными гармониками
()
∑
∞
=
=
0
,cos
k
kk
Dk τωτ
χ
где ;
1
ω
ω
k
k
=
T
π
ω =
1
() ()
∫∫
==
−
TT
T
dk
T
dk
T
D
0
0
2
1
2
1
ττττ
χχ
;
()
T
k ч k
-T
1
D=k
ф cosщфdф
T
∫
()
∫
=
T
k
dk
T
0
cos
1
ττωτ
χ
при
k0
≠
.
Отсюда
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

208
( )
(
)
,coscossinsin
0
KttDttDtt
kkkkkk
k
ωωωω
χ
∞
′′′
=+
∑
=
,
т.е. каноническое разложение корреляционной функции.
Следовательно, и сам стационарный процесс может быть представлен в
виде канонического разложения
() ( )
,sincos
0
∑
∞
=
+=
k
kkkk
tVtUtX ωω
o
где
kk
VU , – некоррелированные случайные величины с нулевыми
математическими ожиданиями и дисперсиями одинаковыми для каждой пары
случайных величин с одним и тем же индексом k.
[
]
[
]
kkk
DVDUD
=
=
.
Дисперсии при различных k определяются по выражению
()
T
k ч k
-T
1
D=k
ф cosщфdф
T
∫
()
∫
=
T
k
dk
T
0
cos
1
ττωτ
χ
при
k0
≠
.
Вот это разложение и называется спектральным.
Спектральное разложение изображает стационарный процесс
разложенным на гармонические колебания различных частот: ,...,,....,,
21 k
ω
ω
ω
причем амплитуды этих колебаний являются случайными величинами.
Дисперсия стационарного процесса равна сумме дисперсий всех
гармоник ее спектрального разложения
∑
∞
=
=
0k
k
DD
χ
.
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

209
Распределение дисперсий по частотам можно проиллюстрировать
графически в виде спектра.
(
)
k
ω
(
)
Dk
0
1
ω
2
ω
3
ω
k
ω
Рис. 73
Мы получили спектр дисперсий в виде ряда дискретных линий.
Попробуем изобразить непрерывный спектр графически. Для этого нужно знать
не саму
k
D , которая безгранично уменьшается при
∞
→
T
, а среднюю
плотность дисперсии, т.е. дисперсию, приходящуюся на единицу длины
данного интервала частот. Обозначим расстояние между соседними частотами
ω
∆
, то есть
ω
π
ω ∆==
T
1
.
На каждом отрезке
ω
∆
, как на основании, построим прямоугольник с
площадью
k
D . Получим ступенчатую диаграмму, напоминающую по принципу
построения гистограмму.
Высота диаграммы на участке
ω
∆
, прилежащем к точке
k
ω
, равна
( )
ω
ω
χ
∆
=
k
k
D
S
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

210
и представляет собой среднюю плотность дисперсии на этом участке (см. рис.
74).
(
)
k
ω
(
)
Xk
S
ω
∆ω
k
D
kX
DD
Σ
=
(
)
X
S
ω
(
)
k
ω
d
ω
Рис. 74
При
0
→
∆
ω
ступенчатая кривая неограниченно приближается к
плавной кривой
(
)
ω
χ
S , которая изображает плотность распределения
дисперсий по частотам непрерывного спектра, а сама функция
(
)
ω
χ
S
называется спектральной плотностью дисперсии или спектральной плотностью
стационарного процесса
;
0
∫
∞
= ωω
χχ
dSD
() ()
∫
∞
=
0
cos ωωτωτ
χχ
dSk .
Спектральная плотность может быть выражена через корреляционную
функцию:
() ()
∫
∞
=
0
cos
2
τωττ
π
ω
χχ
dkS .
На практике часто пользуются нормированной спектральной
плотностью
()
(
)
χ
χ
χ
ω
ω
D
S
S = ,
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com
