Савина Н.В. Применение теории вероятности и методов оптимизации в системах электроснабжения
Подождите немного. Документ загружается.


191
[
]
Мх
,
х
σ
- соответственно математическое ожидание или его
статистическая оценка, среднее квадратичное отклонение
или его статистическая оценка исследуемого ПКЭ.
Равномерный закон распределения.
Вначале определяются границы самого закона распределения
исследуемого ПКЭ из выражений для математического ожидания и дисперсии:
[]
х
х
ав
М ,
2
ва
.
23
σ
+
=
−
=
Отсюда
[]
[]
х
х
х
х
аМ 3,
вМ 3.
σ
σ
=−
=+
Затем находится вероятность попадания возможных значений ПКЭ в
интервалы, заданные ГОСТом при нормально допустимых и предельно
допустимых значениях:
( )
(
П )(П)
( П )(П)
2Н1Н
1Н 2Н
хх
рххх ,
ва
−
≤≤=
−
если
( П )
( П )
2Н
1Н
хв,
ха.
≤
≥
Если
( П )
1Н
ха
<
, то вместо
(
П )
1Н
х в предыдущее выражение подставляется
а, если
( П )
2Н
хв
>
, то в предыдущее выражение вместо
(
П )
2Н
х подставляется в.
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com
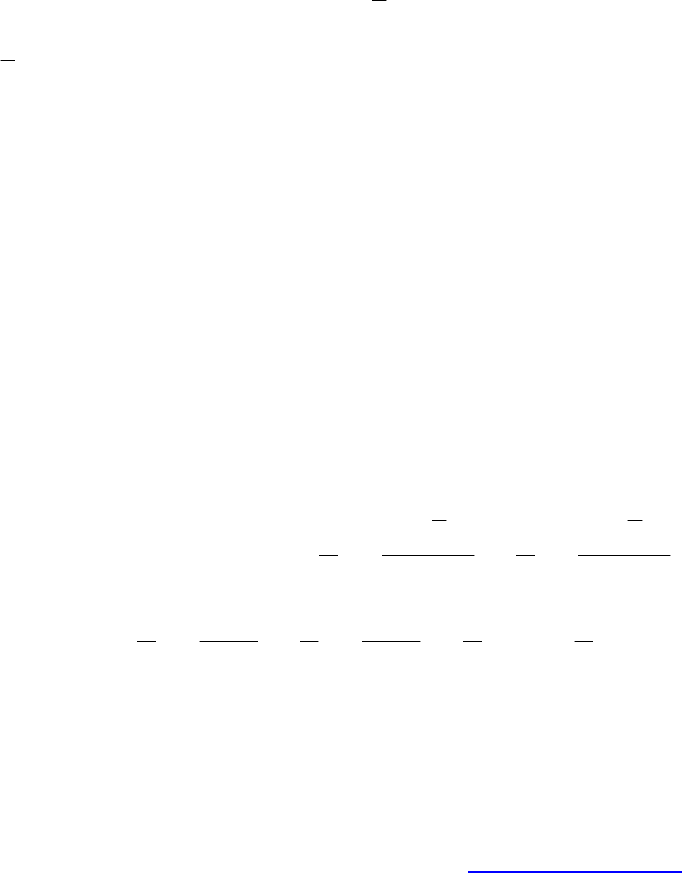
192
4. Найденные вероятности сравниваются с заданными в ГОСТе
значениями. Для оценки соответствия исследуемого ПКЭ нормальным
допустимым значениям найденная вероятность сравнивается с 0,95: если
(
)
1Н 2Н
рххх 0,95
≤≤≥, таким образом требования ГОСТ выполняется, в
противном случае – нет.
Для оценки соответствия исследуемого ПКЭ предельным допустимым
значением найденная вероятность попадания возможных значений ПКЭ в
интервал, определенный предельно допустимыми значениями, сравнивается
с 1. если
(
)
1П 2П
рххх 1
≤≤=
, требования ГОСТ выполняются, в противном
случае – нет.
Пример. Определить соответствие качества электроэнергии требованиям
ГОСТ 13109-97, если в точке общего присоединения (ТОП) оценка
математического ожидания коэффициента несимметрии напряжений по
обратной последовательности
2U
К 1%
= , среднего квадратического отклонения
2U
К
1%
σ
=
при нормальном законе распределения вероятностей.
Согласно ГОСТ нормируемое нормально допустимое значение
2UН
К 2%
= , а предельно допустимое значение
2UП
К 4%
= .
Определим интервалы, заданные ГОСТОм, для нормально допустимых
значений и предельно допустимых значений:
2U2
0
К 2;0К 4
≤≤≤≤
.
Найдем вероятности попадания возможных значений исследуемого
ПКЭ – К
2U
в интервалы, заданные ГОСТ:
( )
() () ()
2U2U
2U
К 2U К 2U
2 К 0 К
11
р0К2ФФ
22
12110111
ФФФ1ф1Ф10,68,
212122
σσ
−−
≤≤=−=
−−
=−=+==
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

193
( )
() ( )
() ()
2U
14110111
р 0 К 4 ФФФ4Ф1
212122
1111
Ф4Ф110,680,84.
2222
−−
≤≤=−=−−=
=+=⋅+⋅=
Сравним найденные вероятности с вероятностями, определенными в
ГОСТе и сделаем вывод об их соответствии
(
)
2U
р 0 К 20,680,95
≤≤=<.
Следовательно, требования ГОСТ 13109-97 по нормально допустимым
значениям не выполняются.
(
)
2U
р 0 К 40,841
≤≤=<
.
Следовательно, требования ГОСТ 13109-97 по предельно допустимым
значениям не выполняются. Необходимо принять меры по поддержанию
требуемого качества электроэнергии.
Пример. Произвести оценку качества электроэнергии на шинах ГПП с
U
ном
= 10 кВ по установившемуся отклонению напряжения, если в результате
измерения оценки математического ожидания и среднего квадратического
отклонения напряжения на шинах соответственно равны
[
]
U
М U10,2кВ,
0,2кВ,σ
=
=
а закон распределения вероятностей равномерный.
Определяем интервалы, заданные ГОСТ 13109-97:
для нормально допустимых значений
у
5%U5%
δ
−≤≤
;
для предельно допустимых значений
у
10%U10%
δ
−≤≤
.
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com
194
Переведем границы интервалов, заданных ГОСТом, в именованные
единицы и выразим их через напряжения:
нормально допустимые значения
9,5U10,5
≤≤
(кВ);
предельно допустимые значения
9U11
≤≤
(кВ).
Определим границы самого закона распределения случайной величины –
напряжения на шинах ГПП, зная математическое ожидание и среднее
квадратическое отклонение:
[
]
[ ]
U
U
аМU3;
вМU3;
σ
σ
=−
=+
()
U
а10,230,29,85кВ;
в 10,230,210,55кВ;
111
f1,43.
ва 10,559,85 кВ
=−⋅=
=+⋅=
===
−−
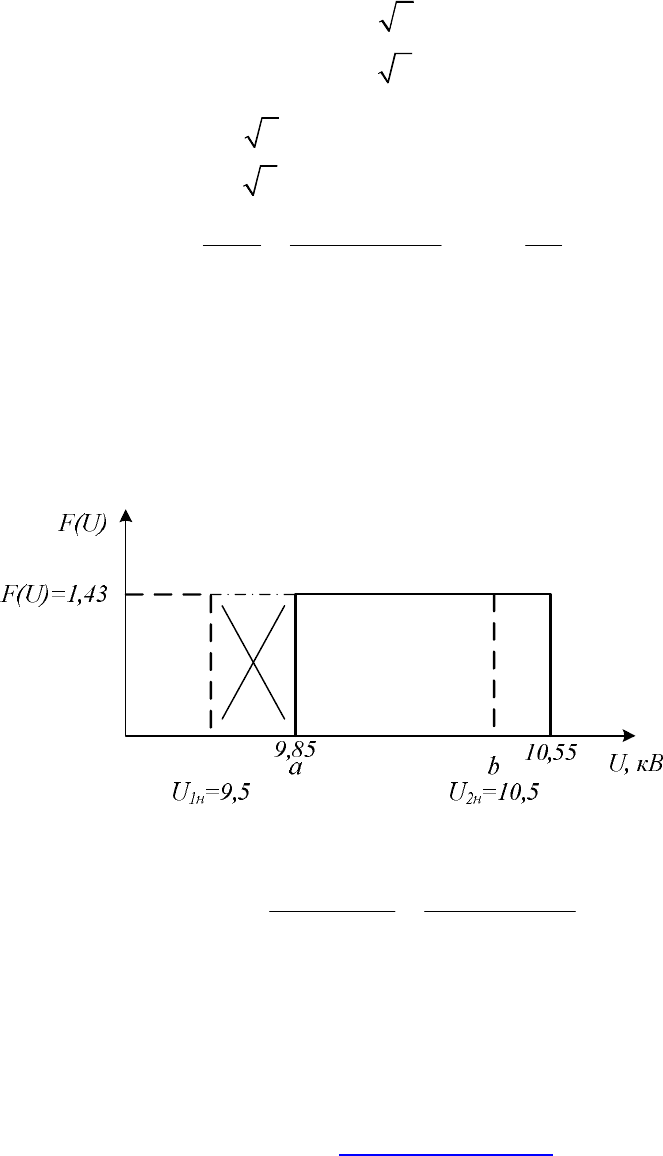
Определим вероятности попадания возможных значений напряжения в
интервалы, заданные ГОСТом.
Для большей наглядности покажем это графически.
Для нормально допустимых значений
( )
2Н 1Н
UU10,59,85
р 9,5U10,50,93
ва 10,559,85
−−
≤≤===
−−
.
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

195
Для предельно допустимых значений
( )
ва
р 9U111
ва
−
≤≤==
−
.
Сравниваем найденные вероятности со значениями вероятностей,
заданными в ГОСТе:
(
)
р 9,5U10,50,930,95
≤≤=<.
Следовательно, требования ГОСТ 13109-97 нормально допустимым
значением не выполняются.
(
)
р 9U1111
≤≤==
.
Следовательно, требования ГОСТ 13109-97 по предельно допустимым
значениям выполняются.
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

196
Вопросы для самопроверки
1. Что понимается под расчетной нагрузкой?
2. Каким образом определяется средняя мощность, максимальная мощность?
3. Что понимается под методической, информационной погрешностью?
4. Как находится относительная среднеквадратическая погрешность расчета
потерь электроэнергии?
5. Как определяются границы интервала неопределенных потерь?
6. Что понимается под надежностью? Как это понятие применяется к
электроэнергетическим системам?
7. Какие типы схем различают при анализе надежности?
8. Какие основные показатели надежности используются в системах
электроснабжения? Как они определяются?
9. Как находится вероятность отказа эквивалентного элемента при
последовательном, параллельном соединении?
10. Каков алгоритм определения ущербов при перерывах в электроснабжении?
11. Какие свойства характеризуют качество электроэнергии?
12. Как влияет отклонение напряжения на работу электроустановок?
13. Как влияет несимметрия напряжения на работу электроустановок и сети в
целом?
14. Как влияют колебания напряжения на работу электроустановок и
технологических механизмов?
15. Причины возникновения электромагнитных помех и их влияние на
электрическую сеть.
16. Какие показатели качества электроэнергии (ПКЭ) используют для
количественного описания свойств качества электроэнергии? Как
нормируются ПКЭ?
17. Каким образом определяется соответствие ПКЭ требованиям ГОСТ 13109-
97?
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

197
Глава 5. Модель «Случайная функция»
5.1. Понятие о случайной функции и случайном процессе
Случайной функцией называется функция, которая в результате опыта
может принять тот или иной конкретный вид, причем неизвестно заранее какой
именно.
Конкретный вид, принимаемый случайной функцией в результате
опыта, называется реализацией случайной функции. Если над случайной
функцией произвести группу опытов, то мы получим «семейство» реализаций
этой функции. Если аргументом функции будет время, то такая случайная
функция называется случайным процессом.
Рассмотрим некоторый случайный процесс X(t). Предположим, что над
ним произведено n независимых опытов, в результате которых получено n
реализаций:
(
)
;
1
tx
(
)
(
)
txtx
n
,...,
2
. Каждая реализация есть неслучайная функция.
Зафиксируем теперь некоторое значение аргумента
i
t , для него случайный
процесс превращается в случайную величину, которую будем называть
сечением случайной функции, соответствующим данному t.
Что же представляет собой закон распределения случайного процесса?
Это должен быть закон распределения случайного процесса, представляющего
собой функцию бесчисленного множества аргументов. Следовательно,
практическое использование его исключено. Но для случайного процесса
можно построить некоторые вероятностные характеристики, аналогичные
законам распределения, которые и позволят анализировать изменения
параметров режима систем электроснабжения во времени.
5.2. Характеристики случайных процессов
Для решения практических задач для случайных процессов вводятся
простейшие основные характеристики, аналогичные числовым
характеристикам случайных величин. Но эти характеристики представляют
собой в общем случае не числа (случайные величины), а функции. Рассмотрим
их.
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com
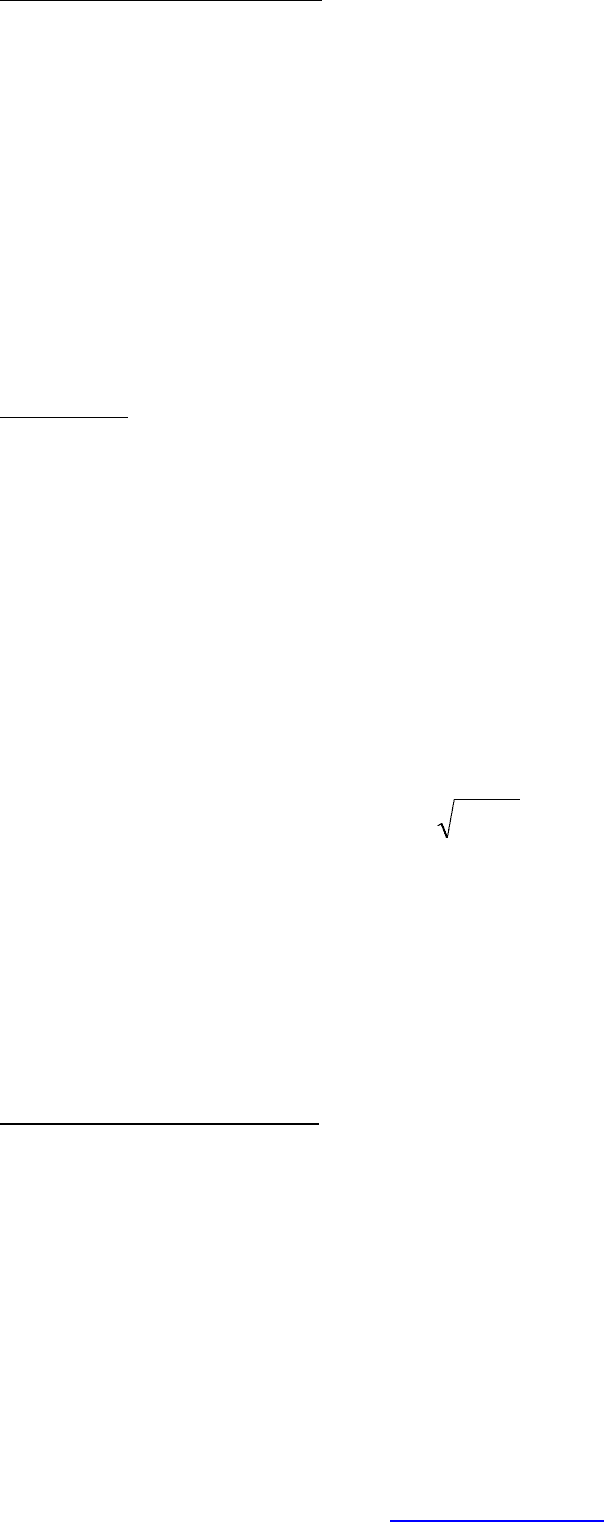
198
Математическое ожидание – неслучайная функция
(
)
[
]
tXM , которая при
каждом значении аргумента t равна математическому ожиданию
соответствующего сечения случайного процесса:
(
)
(
)
[
]
tXMtm
=
χ
.
Таким образом, математическое ожидание по смыслу есть некоторая
средняя функция, около которой различным образом варьируются
конкретные реализации случайного процесса.
Дисперсия – неслучайная функция
(
)
tD
χ
, значение которой для
каждого t равно дисперсии соответствующего сечения случайного процесса:
(
)
(
)
[
]
tXDtD
=
χ
.
Дисперсия случайного процесса при каждом t характеризует разброс
возможных реализаций случайного процесса относительно среднего, то есть
«степень» случайности случайного процесса:
(
)
(
)
tDt
χχ
σ =
.
Однако этих характеристик недостаточно для описания случайного
процесса. Нам необходимо знать внутреннюю структуру, но она не
улавливается ни
()
t
m
χ
, ни
(
)
tD
χ
. Для этого вводится специальная
характеристика – корреляционная (автокорреляционная) функция.
Корреляционная функция характеризует степень зависимости между
сечениями случайного процесса, относящимися к различным моментам
времени t. Степень зависимости величин
(
)
tX и
(
)
tX
′
может быть
охарактеризована их корреляционным моментом. Очевидно он является
функцией двух аргументов
t
и
t
′
и является корреляционной функцией.
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

199
Корреляционной функцией называется неслучайная функция двух
аргументов
(
)
,
Ktt
χ
′
, которая при каждой паре значений
,
tt
′
равна
корреляционному моменту соответствующих сечений случайного
процесса:
( ) () ()
′
=
′
••
tXtXMttK ,
χ
,
где
() () ()
;tmtXtX
χ
−=
•
() () ()
tmtXtX
′
−
′
=
′
•
χ
.
Если
t
t
=
′
, то корреляционная функция обращается в дисперсию
( ) () () () ()
2
,
KttMXtXtMXtDt
χχ
•••
′
===
.
Корреляционная функция симметрична относительно своих аргументов
(
)
(
)
,,
KttKtt
χχ
′′
= .
Вместо корреляционной функции можно пользоваться нормированной
корреляционной функцией
( )
(
)
() ()
,
,
Ktt
Rtt
tt
χ
χ
χχ
σσ
′
′
=
′
, которая представляет собой
коэффициент корреляции величин
(
)
(
)
tXtX
′
, .
Свойства характеристик случайного процесса.
1. При прибавлении к случайному процессу неслучайного слагаемого к
его математическому ожиданию прибавляется то же неслучайное слагаемое:
если
(
)
(
)
(
)
,ttXtY
ϕ
+
=
то
(
)
(
)
(
)
ttmtm
y
ϕ
χ
+
=
.
2. От прибавления неслучайного слагаемого автокорреляционная
функция (АКФ) случайного процесса не меняется:
(
)
(
)
,,
y
KttKtt
χ
′′
= .
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

200
3. При умножении случайного процесса на неслучайный множитель его
математическое ожидание умножается на тот же множитель:
если
(
)
(
)
(
)
,tXttY
ϕ
=
то
(
)
(
)
(
)
tmttm
y χ
ϕ
=
.
4. При умножении случайного процесса на неслучайную функцию его
АКФ умножается на
(
)
(
)
tt
′
ϕ
ϕ
:
(
)
(
)
(
)
(
)
,,
y
KttttKtt
χ
ϕϕ
′′′
= .
Если
(
)
,ct
=
ϕ
то
(
)
(
)
2
,,
y
KttcKtt
χ
′′
= .
Отсюда, когда требуется исследовать АКФ, нужно заранее перейти от
случайной функции к так называемой центрированной функции:
() () ()
.tmtXtX
χ
−=
•
Математическое ожидание центрированной функции тождественно
равно 0, а ее корреляционная функция совпадает с корреляционной функцией
случайного процесса:
(
)
(
)
,,
X
KttKtt
χ
•
′′
= .
Нормированной случайной функцией называется функция вида
()
()
()
t
tX
tX
N
χ
σ
•
= ,
(
)
(
)
,,,
N
X
KttRtt
′′
=
а ее дисперсия = 1.
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com
