Савина Н.В. Применение теории вероятности и методов оптимизации в системах электроснабжения

Подождите немного. Документ загружается.

241

Глава 7. Методы решения оптимизационных задач

7.1. Общие замечания

Анализ структуры математической модели оптимизации показал, что

минимизируемая функция в задаче оптимизации СЭС является сложной

нелинейной функцией большого числа параметров, часть которых может быть

задана дискретно, а ограничения могут быть представлены в виде равенств или

неравенств. В настоящее время задача оптимизации СЭС в целом практически

неразрешима даже при использовании современных ПК. Общую задачу

поэтому расчленяют на ряд частных оптимизационных задач. При этом

принимают упрощающие допущения, позволяющие создавать математические

модели, дающие возможность решать задачу с допустимым приближением.

Решение оптимизационных задач осуществляется методами

математического программирования. Под программированием подразумевается

составление набора значений параметров оптимизации П

, П

, …, П

, при

котором целевая (оптимизируемая) функция достигает какой-либо величины.

Такой набор называется плановым. Набор значений параметров, при котором

целевая функция принимает оптимальную величину, называется оптимальным

планом, а всякие другие значения – допустимыми планами. Мы будем

рассматривать лишь некоторые методы математического программирования,

нашедшие применение при решении задач оптимизации СЭС, – линейного и

нелинейного математического программирования. Методы линейного

программирования применяются для решения оптимизационных задач при

линейной целевой функции и линейных ограничениях. Ограничения при этом

могут быть представлены как в виде равенств, так и неравенств. Методы

нелинейного программирования применяются при нелинейном характере

целевой функции и ограничений. Нелинейные задачи оптимизации могут иметь

несколько решений, т.е. являются многокритериальными. Поэтому при

использовании методов нелинейного программирования приходится

определять вариант, соответствующий экстремуму (наибольшему максимуму

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

242

или наименьшему минимуму) целевой функции в области допустимых

значений оптимизируемых параметров.

В зависимости от вида оптимизируемых параметров оба класса методов

математического программирования подразделяются на подклассы

непрерывного, дискретного и целочисленного программирования. При

нахождении решений для моделей как линейного, так и нелинейного

программирования применительно к реальным электроэнергетическим

оптимизационным задачам процедуры ручного счета практически никогда не

используются. Такого рода работа, как правило, осуществляется с помощью

ЭВМ. Однако, чтобы добиться действительно эффективного и обоснованного

использования методов программирования, исследователь должен понимать

принципы, лежащие в их основе, а не просто обладать умением составлять

математические модели и перекладывать решение на ПК. Разбору сущности

некоторых методов оптимизации и применению их в решении конкретных

оптимизационных задач и посвящен последующий материал.

7.2. Методы линейного программирования применительно к решению

задач оптимизации СЭС

Алгебраическое представление и геометрическая интерпретация метода

линейного программирования

Задачу оптимизации СЭС методом линейного программирования можно

представить следующим образом. Пусть П

является оптимизируемым

параметром

(j = 1, 2, …,k). Требуется определить такие его значения, чтобы

выражение

З(П) = З

+ З

+…+ З

+ …+З

(153)

имело минимальную величину при ограничениях, относящихся в общем виде к

одному из следующих типов:

+ а

+ …+ а

≥ а; (154)

+ b

+ …+ b

= b; (155)

+ с

+…+ с

≤ с. (156)

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

243

Кроме того, могут иметь место ограничения

≥ 0, П

≥ 0, …, П

≥0, …, П

≥ 0. (157)

В частном случае, когда количество переменных П

ограничено двумя или

тремя, задачу можно решить методом графических построений. Для этого

рассмотрим целевую функцию

З(П) = З

+ З

(158)

с ограничениями

+ а

≥ а; (159)

+ b

= b; (160)

+ с

≤ с; (161)

≥ 0; (162)

≥ 0. (163)

Уравнения (159 – 163) в плоскости переменных П

и П

являются

прямыми линиями, которые ограничивают область допустимых решений.

В общем случае она представляет собой многоугольник, любая сторона

которого образована одной их линейных зависимостей (159 – 163), а угол

образуется в результате пересечения двух указанных зависимостей.

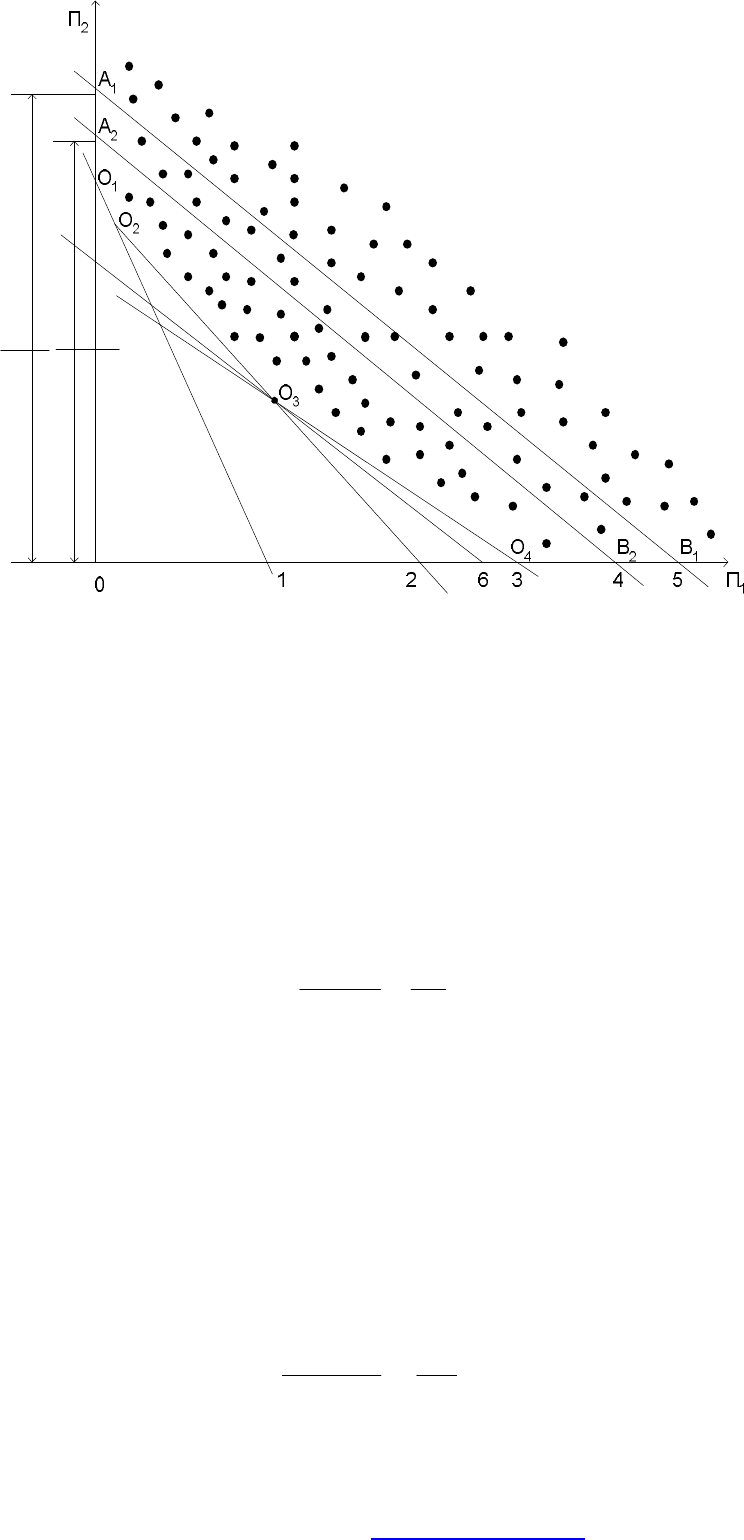
Так, отрезок О

(рис. 79) представляет собой частично зависимость

=0, отрезок О

– частично зависимость а

+ а

= а, отрезок О

–

частично зависимость b

+ b

= b и т.д.

Точка О

образуется при пересечении зависимостей П

=0 и а

+а

= а

и т.п.

Внутренние и граничные точки многоугольника представляют решение

целевой функции, при этом координаты одной или нескольких точек на

плоскости П

могут характеризовать оптимальное значение целевой

функции.

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

244

)

П(З

′

)П(З

′

Рис. 79. Геометрическая интерпретация метода

линейного программирования

Целевая функция (158) в плоскости переменных П

– П

также

представляется прямой линией, которая может быть построена при

фиксированном значении З(П). Так, если принять, что значение З(П) равняется

произвольной величине З´(П), то

)П(З

−

′

(164)

(прямая 5 на рис. 79).

Угол наклона прямой и оси П

определяется отношением коэффициентов

/З

в выражении (164).

Если значение З(П) уменьшить относительно З´(П) и принять равным

З´´(П), то зависимость

)П(З

−

′

(165)

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

245

будет располагаться ниже зависимости З’(П) и параллельно ей (прямая 4 рис.

79).

Нетрудно видеть, что в случае равенства затрат величина З´(П), то есть

область, где может находиться минимальное значение исследуемой целевой

функции, ограничивается многоугольником А

– О

– В

. При

уменьшении значения целевой функции, например при З(П)= З´´(П), область

возможного минимального значения целевой функции уменьшается и

ограничивается многоугольником А

– О

– В

Если принять значение целевой функции еще меньше, то и область

минимальных значений соответственно уменьшится. Очевидно, что целевая

функция может иметь единственную минимальную величину, когда площадь

многоугольника, ограниченного значениями (159 – 163) и зависимостью (158),

будет минимальна, т.е. равна 0. Такой результат будет в том случае, когда

прямая, соответствующая зависимости (158), касается многоугольника

ограничений (прямая 6 на рис. 79).

Как следует из рис. 79, достижение минимального значения целевой

функции возможно лишь тогда, когда область минимальных решений

ограничена снизу.

При решении задачи оптимизации целевой функции (153) и ограничениях

(154 – 157), когда они образуют замкнутый многоугольник:

1) задача может не иметь ни одного допустимого решения, т.е. может не

существовать таких значений параметров, которые удовлетворили бы всем

ограничениям;

2) задача может иметь единственное оптимальное решение, когда прямая,

соответствующая минимуму целевой функции, касается многоугольника

ограничения в одной точке;

3) задача может иметь несколько оптимальных решений, когда прямая,

соответствующая минимуму целевой функции, касается многоугольника

ограничений в нескольких точках. Этот случай возможен при условии

параллельности целевой функции и одной из функций ограничения.

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

246

Применительно к задачам электроэнергетики возможны все три случая.

При этом, если задача оптимизации не имеет ни одного допустимого

решения, то принятое на стадии проектирования инженерное решение должно

отвергаться, так как реализация его в условиях эксплуатации приведет к

неоправданным экологическим затратам или снижению надежности

электроснабжения. Если же такая ситуация будет необходима при

эксплуатации систем электроснабжения, то целесообразно разбить решаемую

оптимизационную задачу на подзадачи и заново решить их. В зависимости от

полученного результата должны выбираться и анализироваться те параметры

оптимизации, которые не удовлетворяют допустимому решению.

В зависимости от результатов такого анализа принимается окончательное

решение по реконструкции или изменению существующей системы

электроснабжения.

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

247

Алгебраические преобразования линейных

оптимизационных моделей

Переход от минимизации к максимизации. В электроэнергетике часто

рассматривают задачи не минимизации функции среднегодовых затрат, а

максимизации функции чистого дисконтированного дохода. В линейном

программировании любая задача минимизации может быть сведена к

эквивалентной задаче максимизации (и наоборот), если одновременно с

изменением «знака» оптимизации произвести изменение знаков перед всеми

коэффициентами в выражении целевой функции. Так, минимизация функции

∑

ПЗ эквивалентна максимизации функции:

∑ ∑

= =

=−

jjjj

ПЭП)З( , (166)

где Э

= -З

(j = 1, 2, …, k).

Переход к эквивалентной системе неравенств. Каждое из неравенств,

фигурирующих в линейной математической модели оптимизации, можно

записать в инверсивной форме, если учесть, что

∑

≥

аПа эквивалентно

∑

≤−

аП)а( . (167)

Обращение неравенства в равенство. Любое неравенство линейной

модели можно представить в виде равенства, если ввести в рассмотрение новую

неотрицательную величину. Это достигается следующим образом:

Неравенство

∑

≥

аПа можно записать в виде

∑

=−

аt1Па , (168)

где t≥0.

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

248

Неравенство

∑

≤

cПc можно записать в виде

∑

cS1Пc , (169)

где S≥0.

Переменную типа t в выражении (168) принято называть избыточной

переменной, а переменную типа S в (169) – остаточной переменной.

Обращение равенств в неравенства. Любое линейное уравнение, а также

любую систему линейных уравнений можно представить в виде некоторой

совокупности линейных неравенств с помощью одного дополнительного

ограничения. Заметим, что равенство П

=10,5 эквивалентно комбинации

неравенств П

≤10,5 и П

≥10,5, которая, в свою очередь, может быть записана в

виде пары неравенств П

≤10,5 и - П

≤ - 10,5. Как нетрудно проверить

графически, система уравнений П

=30, П

=5 эквивалентна комбинации

неравенств П

≤30, П

≤5, П

+П

≥35, которую, в свою очередь, можно записать

следующим образом: П

≤30, П

≤5, - П

-П

≤-35.

Из вышесказанного следует, что систему уравнений

ijji

П b

∑

; (i=1,2,…,l) (170)

можно записать в виде

ijji

П b

≤

∑

; (i=1, 2, …, l);

bП

≤

∑

, (171)

где

jij

∑

=−

∑

. (172)

Т.о., при l =1 соотношения сводятся к следующим:

jjl

П b

≤

∑

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

249

jjl

П b

−≤

∑

В качестве примера рассмотрим систему уравнений:

1537420;

25645.

ПП





−=−



С помощью формул (171) и (172) нетрудно показать, что эта система

эквивалентна следующей системе неравенств:

123

1537420;

25645;

17375225.

ПП

ППП

+≤





−≤−





−−+≤



Переход от параметров, не имеющих ограничения в знаке к

неотрицательным параметрам. Когда для некоторого параметра П

фигурирующего в линейной модели, отсутствует ограничение в знаке, в

процессе нахождения численного решения оказываются полезными следующие

типы преобразований.

1. Вначале выбирается одно из ограничений, содержащее параметр П

записанное в виде равенства (т.е. в виде линейного уравнения). Это всегда

можно сделать (например, после обращения неравенства в равенство). Затем

это уравнение разрешается относительно П

и полученный результат

подставляется во все остальные линейные ограничения, в которых фигурирует

, а также в выражение целевой функции. После этого производятся

упрощения путем приведения подобных членов.

Предположим, что имеем соотношение типа (170), в котором параметр

не ограничен в знаке. Тогда

∑

−=

jj11

)Пbb(

П . (173)

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

250

Правую часть полученного уравнения теперь требуется подставить

вместо П

в те модели, где он фигурирует. Легко убедиться, что полученные в

результате такой подстановки соотношения сохраняют линейный характер и

содержат все параметры кроме П

В процессе нахождения оптимального

решения на уравнение, полученное в результате решения относительно П

выбранного вначале соотношения, можно не обращать внимания. Это

уравнение позволит вычислить П

после того, как будет получено решение для

остальных оптимизируемых параметров.

2. Преобразование второго типа состоит в том, что П

полагается равным

разности двух неотрицательных параметров и, затем, эта разность

подставляется вместо параметра П

всюду, где он фигурирует, т.е. принимается

= П

´- П

´´, где П

´ ≥0 и П

´´≥0.

Данное преобразование увеличивает число параметров в модели,

сохраняя линейность, имевшую место в исходных соотношениях.

3. Преобразование третьего типа заключается в добавлении к каждому

параметру П

, не имеющему ограничения в знаке, одной и той же

неотрицательной переменной с последующим обращением:

≡ П

´ - z,

где П

´≥0 и z≥0.

Пусть параметр П

для j=1, 2, …, n≤k не ограничен в знаке.

Тогда ограничения

∑

ijij

bПb (i= 1, 2, …, l) преобразуются к виду

∑ ∑

= +=

=−+

′

1nj

iijijjij

bzПbПb α ; (i=1, 2, …,l),

где

∑

iji

bα , (i= 1, 2, …, l).

Переход от параметров, значения которых ограничены снизу, к

неотрицательным параметрам. Когда П

ограничен снизу некоторой

константой b

≠0, возможен переход к такой формулировке задачи линейного

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com