Савина Н.В. Применение теории вероятности и методов оптимизации в системах электроснабжения

Подождите немного. Документ загружается.

141

Нанеся полученные значения

()

на гистограмму и соединив их плавной

кривой, получим теоретическую кривую плотности распределения

вероятностей, построенную с использованием статистических оценок

Аналогично можно построить и для F(x):

()

Fx Ф

−







. (107)

Но опять возникает вопрос: а действительно ли именно эта кривая

наиболее точно описывает статистическое распределение? Для решения

вопроса о применимости выдвинутой гипотезы Н

были разработаны критерии

согласия.

3.7. Критерии согласия

Проверка согласованности статистического и теоретического

распределения вероятностей с помощью критериев согласия базируется на

следующем основном положении. Если при статистическом наблюдении

имелись отличия в распределении вероятностей по сравнению с теоретической

кривой для предполагаемого закона распределения вероятностей, то эти

отличия могут иметь две причины:

− слишком мало число испытаний, т.е. мал объем выборки;

− неверна выдвинутая гипотеза Н

о предполагаемом законе

распределения.

Чтобы определить, какая из причин вызывает расхождение, применяют

критерии согласия. Для каждого критерия выбирают определенную величину

меры расхождения, которая и является мерилом степени расхождения между

статистическим и выдвинутым теоретическим законом распределения

вероятностей. Затем для теоретического закона распределения вероятностей

нужно определить при различных числах испытаний

вероятности того, что

мера расхождений

больше или равна некоторого числа, и составить таблицу

вероятностей меры расхождения при данном числе испытаний

−

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

142

Определяют меру расхождения, фактически наблюденную для полученного

статистического материала

. Если она достаточно велика, например 0,8–0,9 и

более, то очевидно, что отличие от теоретического закона получилось только за

счет малого числа испытаний

, и следовательно, гипотеза о законе

распределения вероятностей, принятая ранее, правдоподобна. Если же

вероятность для

мала (0,1–0,2 и менее), то это означает, что отличия от

теоретического закона вызваны неверной гипотезой Н

. Возникает вопрос: как

же выбирать меру расхождения

? Оказывается эта мера и есть критерий

согласия.

Общим для всех критериев согласия является то, что по своей сущности

они отрицательны, т.е. они основаны на так называемом принципе

невозможности маловероятных событий. Мы говорили о нем. Если при

определенных условиях вероятность появления какого-либо события очень

мала, то при однократном осуществлении этого события можно быть

практически уверенным, что это событие не произойдет, т.е. считать его

практически невозможным. С принципом невозможности маловероятных

событий тесно связано понятие уровня значимости

. Так, если

, то мы

считаем практически невозможным событие, которое может появиться в

среднем 5 раз из 100 испытаний. Если

, то практически невозможное

событие – это то событие, которое теоретически возможно только в одном

случае из 100.

На практике в задачах электроэнергетики наиболее часто применяются

следующие критерии согласия: Пирсона, Колмогорова, Романовского и

критерий серий.

Критерий Пирсона

В качестве меры расхождения между теоретическим и статистическим

законами распределения можно взять величину

()

расч

mnp

−

∑

, (108)

где

- номер разряда вариационного ряда;

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

143

- число разрядов вариационного ряда;

- число значений случайной величины, попавших в

-ый разряд

вариационного ряда;

- объем выборки (число испытаний);

- теоретическая вероятность попаданий случайной величины в

-ый

разряд, которая равна

=∆

, (109)

где

ϕ – теоретическая плотность распределения вероятностей.

При всех

расч

. Очевидно, чем больше отличается

от

тем больше будет величина

расч

χ .

Расчетное значение

расч

сравнивается с табличным значением

которое зависит от числа степеней свободы

и уровня значимости

Число степеней свободы

равно

rmk

=−

, (110)

где k – число независимых связей, наложенных на частоты

Оно равно количеству числовых характеристик, достаточных для

аналитического описания закона распределения, плюс 1.

Так, при нормальном законе распределения

213

=+=

, по Пуассону

112

=+=

Для распределения

составлены специальные таблицы. Пользуясь

этими таблицами, можно для каждого значения

и числа степеней свободы

найти вероятность того, что величина, распределенная по закону

превзойдет это значение. Входными в этих таблицах являются: либо значение

вероятности

, либо уровень значимости

αβ

=−

и число степеней свободы

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

144

. Числа, стоящие в строках таблиц, представляют собой соответствующие

значения

Итак, порядок применения критерия

к оценке согласованности

теоретического и статистического распределений следующий:

1) определить расчетное значение критерия Пирсона

расч

χ ;

2) определить число степеней свободы

rmk

=−

;

3) выбрать уровень значимости

(обычно

0,10,05

или

);

4) По таблице /4/определить

;

5) Сравнить

расч

χ с

Если

расч

≤

, то выдвинутая гипотеза Н

верна, разница объясняется

малым объемом выборки, но достаточным для выбранной вероятности β. Если

расч

χ >

, то гипотеза Н

отвергается. В этом случае нужно либо увеличить

, либо принять другой теоретический закон распределения.

Критерий Пирсона применяется при любом известном и неизвестном

законе распределения вероятностей.

Критерий Колмогорова

Если заранее известен закон распределения случайной величины и ее

основные числовые характеристики, то можно использовать критерий

Колмогорова.

В качестве меры расхождения между теоретическим и статистическим

распределениями по критерию Колмогорова рассматривают максимальное

значение модуля разности между статистической функцией распределения

()

и соответствующей теоретической функцией распределения:

max

()()

DFxFx=− . (111)

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

145

Колмогоров доказал, что какова бы ни была функция распределения F(x)

непрерывной случайной величины Х, при неограниченном увеличении числа

независимых наблюдений

, вероятность неравенства

≥

(112)

стремится к пределу

()1(1)

∞

−

=−∞

=−−

∑

. (113)

Порядок применения критерия Колмогорова следующий:

1) строится статистическая функция распределения

()

;

2) строится теоретическая функция распределения

()

;

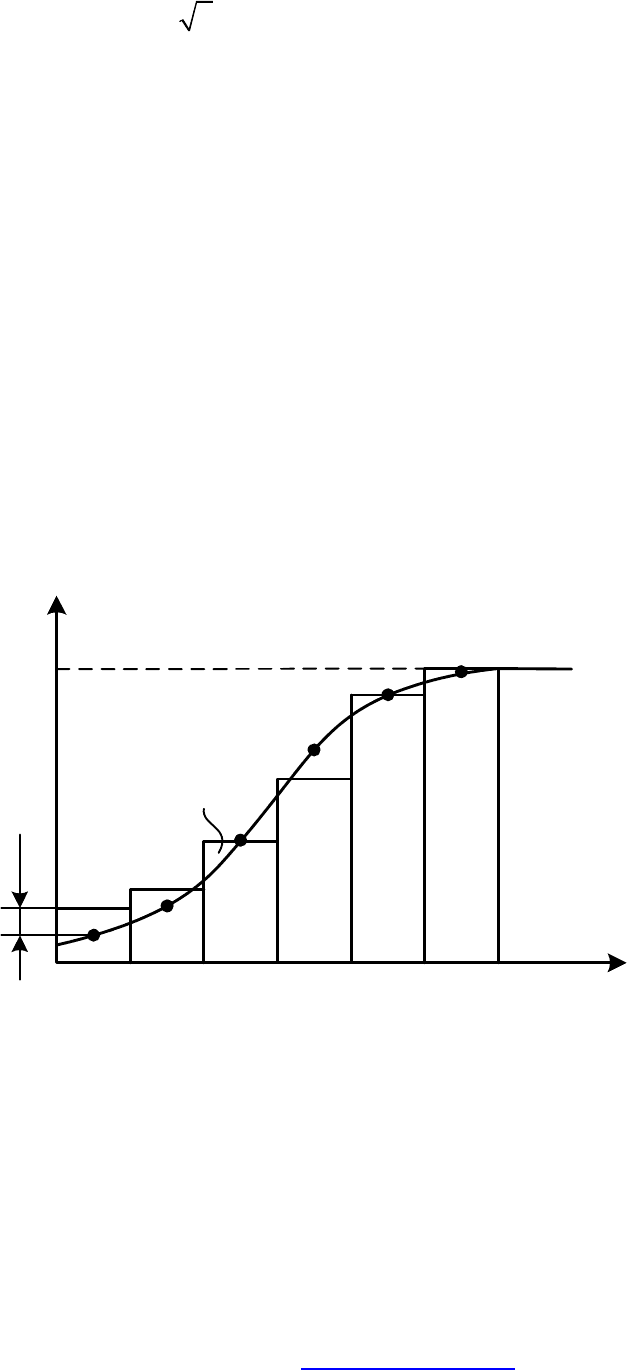
3) определяется максимум модуля разности между ними

max

(см. рис.

64);

()

max

Рис. 64. Определение максимума модуля разности

между

()

max

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

146

4) определяется величина

по выражению

max

λ = ; (114)

5) по таблице /4/ находится вероятность

()

того, что для

теоретической функции распределения

()

при данном числе испытаний мера

расхождения будет равна или больше

. То есть, вероятность того, что если

случайная величина х действительно распределена по закону

()

за счет

чисто случайных причин, максимальное расхождение между

()

будет не меньше, чем фактически наблюденное. Если вероятность

()

весьма

мала, гипотезу следует отвергнуть как неправдоподобную. При сравнительно

больших значениях

()

ее можно считать совместимой с опытными данными.

Необходимо отметить, что в задачах систем электроснабжения применять

критерий Колмогорова целесообразно только в том случае, если

гипотетическое распределение

()

полностью известно заранее из каких-либо

теоретических соображений, т.е. когда известен не только вид

()

, но и

входящие в нее параметры.

Пример.

При исследовании мощности вводного присоединения понизительной

подстанции было проведено 100 испытаний. По ним построены статистическая

функция распределения

()

и теоретическая

()

, соответствующая

нормальному распределению. Максимальный модуль разности между

()

составил

max

=0,04. Проверить по критерию Колмогорова верность

выдвинутой гипотезы о нормальном распределении.

Определяем

max

0,041000,4

Dnλ===.

По таблице /4/ находим

()

()(0,4)0,997

Выдвинутая гипотеза верна.

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

147

Критерий Романовского

Если число степеней свободы достаточно велико

≥

, то проверку

согласия теоретического и статистического распределения вероятностей можно

осуществлять по критерию

и без таблиц критических значений с помощью

критерия Романовского

расч

−

= . (115)

Если

- гипотеза Н

отвергается, если

- гипотеза Н

верна.

Критерий серий

Этот критерий является одним из наиболее широко применяемых

критериев в задачах систем электроснабжения. Так же, как и критерий

применение критерия серий не накладывает каких-либо ограничений на тип

распределения случайной величины. Такие критерии называются

независящими от формы распределения вероятностей или

непараметрическими.

Рассмотрим последовательность N наблюденных значений случайной

величины Х и каждое наблюденное значение отнесем к одной из двух взаимно

исключающих категорий, которые можно просто обозначить знаками (+) и (-).

Например, имеется последовательность измеренных величин

,1,2...

XiN

среднее значение которых равно

. Тогда каждому

≥

присвоим знак (+),

а каждому значению

знак (-). Или, имеем последовательность пар

наблюдений

. Например, значения

()

, где

1,2,...

Примем, если

≥

, т.е.

()

≥

()

, то ставим (+), если

, то есть

()

, то знак (-).

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

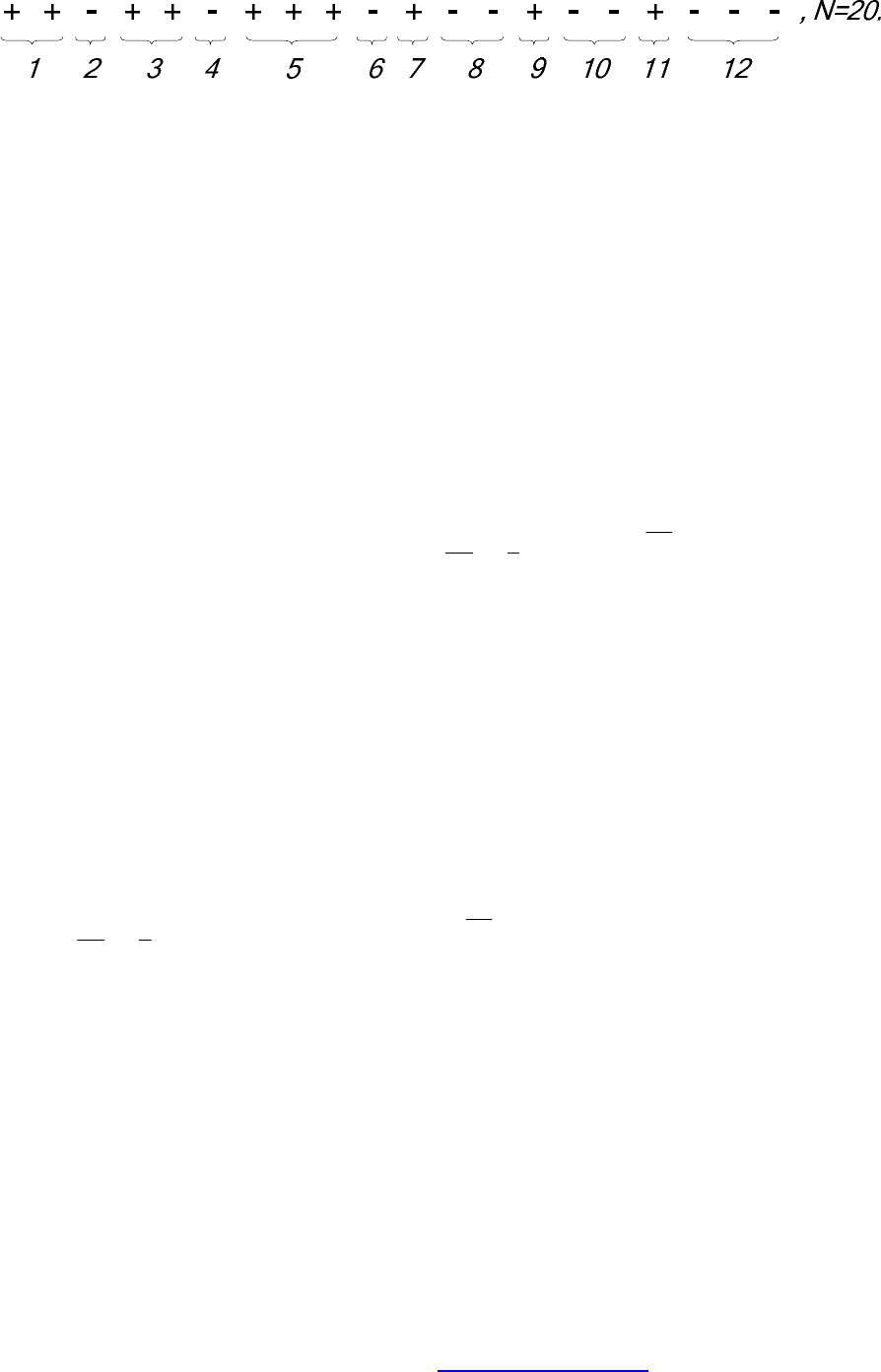
148

В любом из этих случаев последовательность наблюдений может иметь

вид:

Серией назовем последовательность наблюденных значений, перед

которыми и после которых расположены наблюденные значения другой

категории или наблюдения отсутствуют вообще.

Число серий, которое встречается в последовательности наблюдений,

позволяет определять, являются ли результаты наблюдения независимыми

случайными величинами. Гипотезу проверяют при принятом уровне

значимости α путем сопоставления наблюденного числа серий r с табличными

граничными значениями числа

табл

rrr

αα−







, где

. Если

выходит за

границы этого интервала, гипотезу отвергают при принятом

. В противном

случае гипотезу принимают.

В рассмотренном выше случае из N=20 наблюдений значений тока ЭП

имеем 12 серий. По гистограмме выдвигаем гипотезу, что ток распределен по

нормальному закону. Область принятия гипотезы определяется границами:

110,0.97510,0.025

;;

rrrr

αα−







, где

10;0.05

n α===.

По таблице /25/ при n=10 и

0.05

находим

10,0.97510,0.025

6;14

Тогда 6<12<14.

Таким образом, гипотеза о нормальном законе распределения

вероятностей тока принимается.

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

149

3.8. Примеры статистических исследований случайных величин в

электроэнергетике

Задача 1. Проведено 100 измерений значений тока ввода №1

распределительной подстанции (РП) глиноземного комбината. Результаты

измерений следующие:

0,71; 0,75; 0,57; 0,58; 0,4; …; 0,85; 1,55; 1,88; …; 1,9 кА.

Будем считать, что в указанные значения тока попали минимальное и

максимальное.

Определить статистическую плотность распределения вероятностей тока

и аппроксимировать ее одним из известных законов распределения

вероятностей. Найти интервальную оценку математического ожидания тока

ввода №1 РП.

Решение.

Объем выборки n=100.

Результаты измерений тока сводим в простой статистический ряд.

№ опыта 1 2 3 4 5 … k k+1 k+2 …

Значение тока, кА

0,71 0,75 0,57 0,58 0,42 … 0,85 1,55 1,88 …

Обрабатываем простой статистический ряд и строим вариационный ряд.

Для этого разделим весь диапазон измеренных значений тока на интервалы или

разряды и подсчитаем количество значений,

, приходящееся на каждый j-й

разряд, то есть число попаданий результатов измерения тока в каждый j-й

разряд. Сумма чисел попаданий должна быть равна числу измерений.

Число попаданий разделим на общее число наблюдений n и найдем

частоту, соответствующую j-му разряду:

= .

Сумма частот всех разрядов должна быть равна 1.

Выбираем 10 разрядов, т.е. m=10 и определим длину разряда:

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

150

maxmin

I-I1,9-0,4

=0,15

1010

≈ .

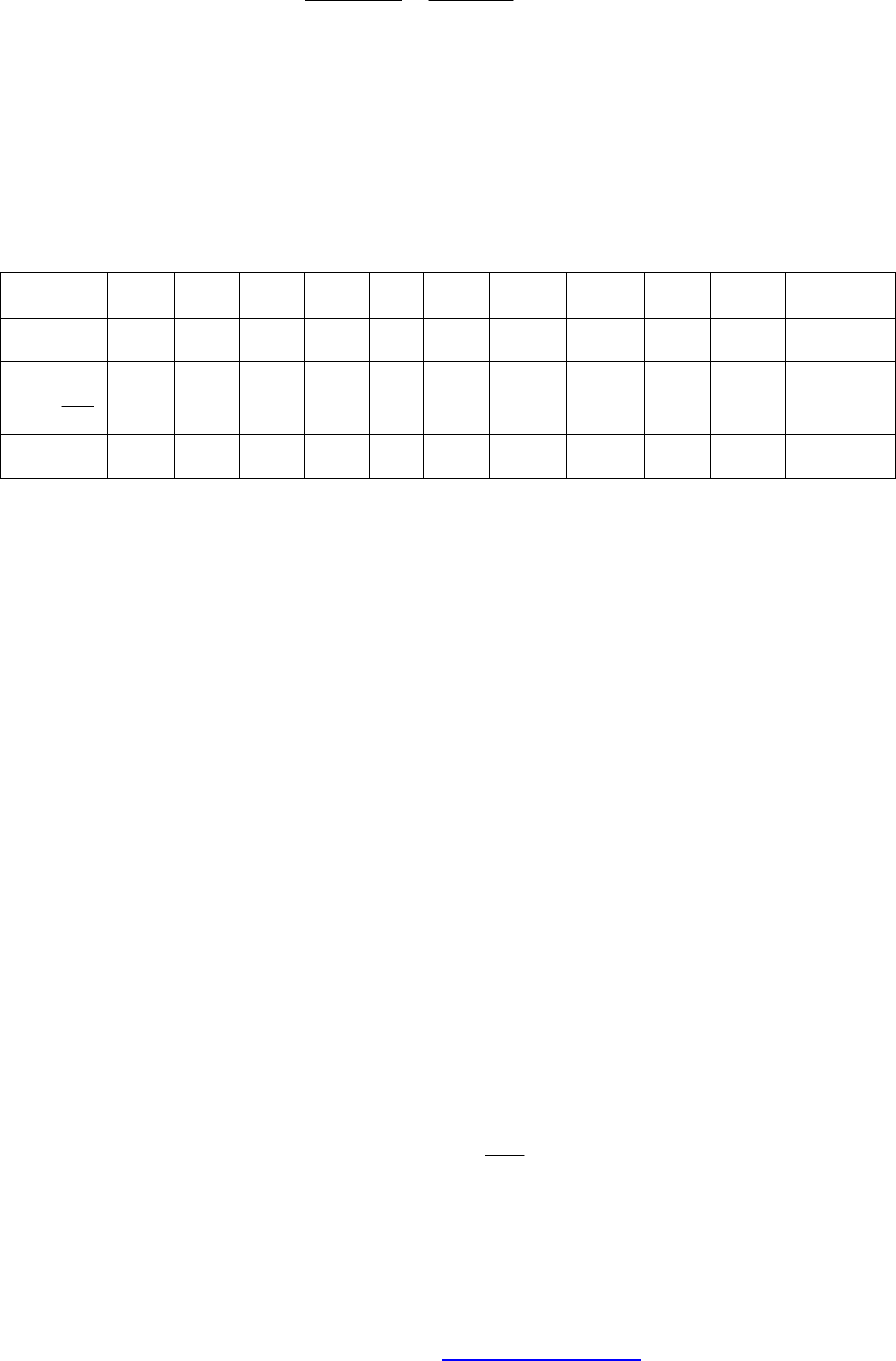
Построим таблицу, в которой приведены разряды (интервалы) в порядке

их расположения вдоль оси абсцисс и соответствующие им частоты.

Эта таблица и есть вариационный ряд.

I, кА

0,4-0,55

0,55-0,7

0,7-0,85

0,85-1

1-1,15

1,15-1,3

1,3-1,45

1,45-1,6

1,6-1,75

1,75-1,9

;

1 3 9 17 23 22 15 7 2 1

100

∑

0,01 0,03 0,09 0,17 0,23 0,22 0,15 0,07 0,02 0,01

∑

()

0,07 0,02 0,6 1,13 1,53 1,45 1 0,45 0,13 0,07

()

Если при группировке измеренных значений случайной величины, I,

имеется значение, находящееся в точности на границе раздела двух разрядов,

то его нужно считать принадлежащим в равной мере к обоим разрядам и

прибавить к числам

того и другого разряда по 0,5.

Вариационный ряд оформляется графически в виде гистограммы.

Гистограмма строится следующим образом. По оси абсцисс

откладываются разряды, и на каждом из них как на основании строится

прямоугольник, площадь которого равна частоте данного разряда.

Следовательно, для построения гистограммы нужно частоту каждого разряда

разделить на его длину и полученное число взять в качестве высоты h

прямоугольника.

Определим высоты

∆

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com